Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-23T06:27:47.542Z Has data issue: false hasContentIssue false
  • English
  • Français

A BETTER COMPARISON OF 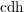$\operatorname{cdh}$- AND 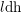$l\operatorname{dh}$-COHOMOLOGIES

Part of: Categories and geometry Algebraic geometry: Foundations (Co)homology theory

Published online by Cambridge University Press:  13 September 2019

SHANE KELLY Open the ORCID record for SHANE KELLY [Opens in a new window]
SHANE KELLY*
Affiliation:
Department of Mathematics, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo 152-8551, Japan email shanekelly@math.titech.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

In order to work with non-Nagata rings which are Nagata “up-to-completely-decomposed-universal-homeomorphism,” specifically finite rank Hensel valuation rings, we introduce the notions of pseudo-integral closure, pseudo-normalization, and pseudo-Hensel valuation ring. We use this notion to give a shorter and more direct proof that 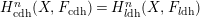$H_{\operatorname{cdh}}^{n}(X,F_{\operatorname{cdh}})=H_{l\operatorname{dh}}^{n}(X,F_{l\operatorname{dh}})$ for homotopy sheaves 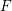$F$ of modules over the 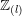$\mathbb{Z}_{(l)}$-linear motivic Eilenberg–Maclane spectrum. This comparison is an alternative to the first half of the author’s volume Astérisque 391 whose main theorem is a cdh-descent result for Voevodsky motives. The motivating new insight is really accepting that Voevodsky’s motivic cohomology (with 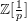$\mathbb{Z}[\frac{1}{p}]$-coefficients) is invariant not just for nilpotent thickenings, but for all universal homeomorphisms.

MSC classification

Primary: 14A05: Relevant commutative algebra 18F10: Grothendieck topologies 14F42: Motivic cohomology; motivic homotopy theory
Type
Article
Information
Nagoya Mathematical Journal , Volume 236: Celebrating the 60th Birthday of Shuji Saito , December 2019 , pp. 183 - 213
Copyright
© 2019 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhatt, B. and Mathew, A., The arc-topology, 2018.Google Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXX. Algèbre commutative. Chapitre 5: Entiers. Chapitre 6: Valuations, Actualités Scientifiques et Industrielles, No. 1308, Hermann, Paris, 1964.Google Scholar
Cisinski, D.-C. and Déglise, F., “ Integral mixed motives in equal characteristic ”, in Documenta Math. Extra Volume: Alexander S. Merkurjev’s Sixtieth Birthday, 2015, 145–194.Google Scholar
Colliot-Thélene, J.-L., Hoobler, R. T. and Kahn, B., The Bloch–Ogus–Gabber theorem , Algebraic K-theory (Toronto, ON, 1996) 16 (1997), 31–94.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphismes , Inst. Hautes Études Sci. Publ. Math. 8 (1961), 222.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II , Inst. Hautes Études Sci. Publ. Math. 24 (1965), 231.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas, troisième partie , Inst. Hautes Études Sci. Publ. Math. 28 (1966), 255. Revised in collaboration with Jean Dieudonné. Freely available on the Numdam web site at http://www.numdam.org/numdam-bin/feuilleter?id=PMIHES_1966__28_.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV , Inst. Hautes Études Sci. Publ. Math. 32 (1967), 361. Revised in collaboration with Jean Dieudonné. Freely available on the Numdam web site at http://www.numdam.org/numdam-bin/feuilleter?id=PMIHES_1967__32_.Google Scholar
Elmanto, E. and Khan, A. A., Perfection in motivic homotopy theory, 2018.10.1112/plms.12280Google Scholar
Engler, A. J. and Prestel, A., Valued Fields, Springer Science & Business Media, Berlin/Heidelberg, 2005.Google Scholar
Gabber, O. and Kelly, S., Points in algebraic geometry , J. Pure Applied Algebra 219(10) (2015), 4667–4680.10.1016/j.jpaa.2015.03.001Google Scholar
Huber, A. and Kelly, S., Differential forms in positive characteristic II: cdh-descent via functorial Riemann–Zariski spaces , Algebra and Number Theory Forthcoming, 2018. Preprint arXiv:1706.05244.Google Scholar
Kashiwara, M. and Schapira, P., Categories and Sheaves, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 332 , Springer-Verlag, Berlin, 2006.Google Scholar
Kelly, S., Triangulated categories of motives in positive characteristic. PhD thesis, Université Paris 13, Australian National University, 2012. Preprint arXiv:1305.5349.Google Scholar
Kelly, S., Vanishing of negative K-theory in positive characteristic , Compos. Math. 150(8) (2014), 1425–1434.10.1112/S0010437X14007301Google Scholar
Kelly, S., Voevodsky motives and ldh-descent , Astérisque 391 (2017), iv+125.Google Scholar
Kelly, S. and Morrow, M., $K$ -theory of valuation rings, 2018.Google Scholar
Matsumura, H., Commutative Ring Theory, 2nd edn, Cambridge Studies in Advanced Mathematics 8 , Cambridge University Press, Cambridge, 1989, Translated from the Japanese by M. Reid.Google Scholar
Quillen, D., Higher Algebraic K-Theory: I, 85–147. Springer, Berlin, Heidelberg, 1973.10.1007/BFb0067053Google Scholar
Raynaud, M. and Gruson, L., Critères de platitude et de projectivité. Techniques de “platification” d’un module , Invent. Math. 13 (1971), 1–89.10.1007/BF01390094Google Scholar
Rydh, D., Submersions and effective descent of étale morphisms , Bull. Soc. Math. France 138 (2010), 181–230.10.24033/bsmf.2588Google Scholar
Théorie des topos et cohomologie étale des schémas. Tome 1: Théorie des topos. Lecture Notes in Mathematics, Vol. 269. Springer-Verlag, Berlin, 1972. Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck, et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat.Google Scholar
Théorie des topos et cohomologie étale des schémas. Tome 2. Lecture Notes in Mathematics, Vol. 270. Springer-Verlag, Berlin, 1972. Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4), Dirigé par M. Artin, A. Grothendieck et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat.Google Scholar
The Stacks Project Authors. Stacks Project. http://stacks.math.columbia.edu, 2014.Google Scholar
Temkin, M., Relative Riemann–Zariski spaces , Israel J. Mathematics 185(1) (2011), 1–42.10.1007/s11856-011-0099-0Google Scholar
Voevodsky, V., Homology of schemes , Selecta Math. (N.S.) 2(1) (1996), 111–153.Google Scholar
Voevodsky, V., “ Triangulated categories of motives over a field ”, in Cycles, Transfers, and Motivic Homology Theories, Ann. of Math. Stud. 143 , Princeton University Press, Princeton, NJ, 2000, 188–238.Google Scholar
Voevodsky, V., “ Cohomological theory of presheaves with transfers ”, in Cycles, Transfers, and Motivic Homology Theories, Ann. of Math. Stud. 143 , Princeton Univ. Press, Princeton, NJ, 2000, 87–137.Google Scholar