Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-16T06:20:48.996Z Has data issue: false hasContentIssue false
  • English
  • Français

Gröbner bases for quadratic algebras of skew type

Part of: Rings and algebras arising under various constructions Semigroups Theory of computing

Published online by Cambridge University Press:  16 March 2012

Ferran Cedó  and
Jan Okniński
Ferran Cedó
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain
Jan Okniński
Affiliation:
Institute of Mathematics, Warsaw University, Banacha 2, 02-097 Warsaw, Poland (okninski@mimuw.edu.pl)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Non-degenerate monoids of skew type are considered. This is a class of monoids S defined by n generators and 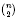quadratic relations of certain type, which includes the class of monoids yielding set-theoretic solutions of the quantum Yang–Baxter equation, also called binomial monoids (or monoids of I-type with square-free defining relations). It is shown that under any degree-lexicographic order on the associated free monoid FMn. of rank n the set of normal forms of elements of S is a regular language in FMn. As one of the key ingredients of the proof, it is shown that an identity of the form xN yN = yN xN holds in S. The latter is derived via an investigation of the structure of S viewed as a semigroup of matrices over a field. It also follows that the semigroup algebra K[S] is a finite module over a finitely generated commutative subalgebra of the form K[A] for a submonoid A of S.

Keywords

finitely presented semigroupsemigroup ringsemigroupnormal formregular language

MSC classification

Secondary: 16S15: Finite generation, finite presentability, normal forms (diamond lemma, term-rewriting) 16S36: Ordinary and skew polynomial rings and semigroup rings 20M05: Free semigroups, generators and relations, word problems 20M20: Semigroups of transformations, etc. 20M25: Semigroup rings, multiplicative semigroups of rings 20M35: Semigroups in automata theory, linguistics, etc. 68Q70: Algebraic theory of languages and automata
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 55 , Issue 2 , June 2012 , pp. 387 - 401
Copyright
Copyright © Edinburgh Mathematical Society 2012

References

1.Anan′in, A. Z., An intriguing story about representable algebras, in Ring theory, pp. 31–38 (Weizmann Science Press, Jerusalem, 1989).Google Scholar
2.Bell, J. P. and Colak, P., Primitivity of finitely presented monomial algebras, J. Pure Appl. Alg. 213 (2009), 1299–1305.Google Scholar
3.Gateva-Ivanova, T., Skew polynomial rings with binomial relations, J. Alg. 185 (1996), 710–753.Google Scholar
4.Gateva-Ivanova, T., Quadratic algebras, Yang–Baxter equation, and Artin–Schelter regularity, preprint (arXiv:1011.6520).Google Scholar
5.Gateva-Ivanova, T. and Van den Bergh, M., Semigroups of I-type, J. Alg. 206 (1998), 97–112.CrossRefGoogle Scholar
6.Gilmer, R., Commutative semigroup rings (University of Chicago Press, 1984).Google Scholar
7.Jespers, E. and Okniński, J., Noetherian semigroup algebras (Springer, 2007).CrossRefGoogle Scholar
8.Lallement, G., Semigroups and combinatorial applications (Wiley, 1979).Google Scholar
9.Månsson, J. and Nordbeck, P., Regular Gröbner bases, J. Symb. Computat. 33 (2002), 163–281.Google Scholar
10.Månsson, J. and Nordbeck, P., A generalized Ufnarovski graph, in Applied algebra, algebraic algorithms and error-correcting codes, Lecture Notes in Computer Science, Volume 3857, pp. 293–306 (Springer, 2005).Google Scholar
11.Okniński, J., Semigroup algebras (Marcel Dekker, New York, 1991).Google Scholar
12.Okniński, J., Semigroups of matrices (World Scientific, Singapore, 1998).Google Scholar
13.Okniński, J., Structure of prime finitely presented monomial algebras, J. Alg. 320 (2008), 3199–3205.CrossRefGoogle Scholar
14.Passman, D. S., The algebraic structure of group rings (Wiley-Interscience, New York, 1977).Google Scholar
15.Rump, W., A decomposition theorem for square-free unitary solutions of the quantum Yang–Baxter equation, Adv. Math. 193 (2005), 40–55.CrossRefGoogle Scholar
16.Ufnarovskii, V. A., Combinatorial and asymptotic methods in algebra, in Encyclopedia of Mathematical Sciences, Volume 57, pp. 1–196 (Springer, 1995).Google Scholar