Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Boscaggin, Alberto
and
Garrione, Maurizio
2016.
Positive solutions to indefinite Neumann problems when the weight has positive average.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 10,
p.
5231.
Feltrin, Guglielmo
and
Zanolin, Fabio
2017.
Multiplicity of positive periodic solutions in the superlinear indefinite case via coincidence degree.
Journal of Differential Equations,
Vol. 262,
Issue. 8,
p.
4255.
Jiao, Lishuai
and
Zhang, Xuemei
2018.
A class of second-order nonlocal indefinite impulsive differential systems.
Boundary Value Problems,
Vol. 2018,
Issue. 1,
Boscaggin, Alberto
and
Feltrin, Guglielmo
2018.
Positive subharmonic solutions to nonlinear ODEs with indefinite weight.
Communications in Contemporary Mathematics,
Vol. 20,
Issue. 01,
p.
1750021.
Sovrano, Elisa
2018.
A negative answer to a conjecture arising in the study of selection–migration models in population genetics.
Journal of Mathematical Biology,
Vol. 76,
Issue. 7,
p.
1655.
Feltrin, Guglielmo
2018.
Positive subharmonic solutions to superlinear ODEs with indefinite weight.
Discrete & Continuous Dynamical Systems - S,
Vol. 11,
Issue. 2,
p.
257.
Xu, Man
and
Ma, Ruyun
2018.
Discrete Neumann boundary value problem for a nonlinear equation with singular ϕ-Laplacian.
Advances in Difference Equations,
Vol. 2018,
Issue. 1,
Feltrin, Guglielmo
and
Sovrano, Elisa
2018.
An indefinite nonlinear problem in population dynamics: high multiplicity of positive solutions.
Nonlinearity,
Vol. 31,
Issue. 9,
p.
4137.
Hakl, Robert
and
Zamora, Manuel
2019.
Existence and Multiplicity of Periodic Solutions to Indefinite Singular Equations Having a Non-monotone Term with Two Singularities.
Advanced Nonlinear Studies,
Vol. 19,
Issue. 2,
p.
317.
Boscaggin, Alberto
and
Feltrin, Guglielmo
2020.
Positive periodic solutions to an indefinite Minkowski-curvature equation.
Journal of Differential Equations,
Vol. 269,
Issue. 7,
p.
5595.
Boscaggin, Alberto
and
Feltrin, Guglielmo
2020.
Pairs of positive radial solutions for a Minkowski-curvature Neumann problem with indefinite weight.
Nonlinear Analysis,
Vol. 196,
Issue. ,
p.
111807.
Boscaggin, Alberto
Feltrin, Guglielmo
and
Sovrano, Elisa
2020.
High Multiplicity and Chaos for an Indefinite Problem Arising from Genetic Models.
Advanced Nonlinear Studies,
Vol. 20,
Issue. 3,
p.
675.
Feltrin, Guglielmo
and
Gidoni, Paolo
2020.
Multiplicity of clines for systems of indefinite differential equations arising from a multilocus population genetics model.
Nonlinear Analysis: Real World Applications,
Vol. 54,
Issue. ,
p.
103108.
Amster, Pablo
Benevieri, Pierluigi
and
Haddad, Julián
2021.
Periodic positive solutions of superlinear delay equations via topological degree.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 379,
Issue. 2191,
p.
20190373.
Yang, Hujun
and
Han, Xiaoling
2023.
Existence and Uniqueness of Periodic Solutions for a Class of Higher Order Differential Equations.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 5,
Boscaggin, Alberto
Feltrin, Guglielmo
and
Zanolin, Fabio
2023.
Positive solutions for a Minkowski-curvature equation with indefinite weight and super-exponential nonlinearity.
Communications in Contemporary Mathematics,
Vol. 25,
Issue. 04,
Zhao, Zhongzi
and
Ma, Ruyun
2023.
Global bifurcation of positive solutions of a quasilinear indefinite Neumann problem in some FLRW spacetimes.
Journal of Mathematical Physics,
Vol. 64,
Issue. 7,
Ma, Ruyun
Zhao, Zhongzi
and
Su, Xiaoxiao
2024.
Global structure of positive and sign-changing periodic solutions for the equations with Minkowski-curvature operator.
Advanced Nonlinear Studies,
Vol. 0,
Issue. 0,
Su, Xiaoxiao
Yan, Meng
and
Ma, Ruyun
2024.
GLOBAL STRUCTURE OF POSITIVE SOLUTIONS FOR FIRST-ORDER DISCRETE PERIODIC BOUNDARY VALUE PROBLEMS WITH INDEFINITE WEIGHT.
Journal of Applied Analysis & Computation,
Vol. 14,
Issue. 1,
p.
119.
Ma, Ruyun
Yang, Lijuan
and
Zhang, Yali
2024.
Global structure of positive solutions for p-Laplacian Neumann problem with indefinite weight.
Computational and Applied Mathematics,
Vol. 43,
Issue. 3,




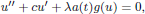
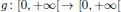 is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when
is a sublinear function at infinity having superlinear growth at zero. We prove the existence of two positive solutions when