Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-18T07:00:44.777Z Has data issue: false hasContentIssue false
  • English
  • Français

Scale-dependent alignment, tumbling and stretching of slender rods in isotropic turbulence

Published online by Cambridge University Press:  07 December 2018

Nimish Pujara Open the ORCID record for Nimish Pujara [Opens in a new window] ,
Greg A. Voth Open the ORCID record for Greg A. Voth [Opens in a new window]  and
Evan A. Variano
Nimish Pujara
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
Greg A. Voth
Affiliation:
Department of Physics, Wesleyan University, Middletown, CT 06459, USA
Evan A. Variano
Affiliation:
Department of Civil and Environmental Engineering, University of California, Berkeley, CA 94720, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the dynamics of slender, rigid rods in direct numerical simulation of isotropic turbulence. The focus is on the statistics of three quantities and how they vary as rod length increases from the dissipation range to the inertial range. These quantities are (i) the steady-state rod alignment with respect to the perceived velocity gradients in the surrounding flow, (ii) the rate of rod reorientation (tumbling) and (iii) the rate at which the rod end points move apart (stretching). Under the approximations of slender-body theory, the rod inertia is neglected and rods are modelled as passive particles in the flow that do not affect the fluid velocity field. We find that the average rod alignment changes qualitatively as rod length increases from the dissipation range to the inertial range. While rods in the dissipation range align most strongly with fluid vorticity, rods in the inertial range align most strongly with the most extensional eigenvector of the perceived strain-rate tensor. For rods in the inertial range, we find that the variance of rod stretching and the variance of rod tumbling both scale as 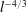$l^{-4/3}$, where 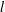$l$ is the rod length. However, when rod dynamics are compared to two-point fluid velocity statistics (structure functions), we see non-monotonic behaviour in the variance of rod tumbling due to the influence of small-scale fluid motions. Additionally, we find that the skewness of rod stretching does not show scale invariance in the inertial range, in contrast to the skewness of longitudinal fluid velocity increments as predicted by Kolmogorov’s 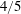$4/5$ law. Finally, we examine the power-law scaling exponents of higher-order moments of rod tumbling and rod stretching for rods with lengths in the inertial range and find that they show anomalous scaling. We compare these scaling exponents to predictions from Kolmogorov’s refined similarity hypotheses.

JFM classification

Turbulent Flows: Intermittency Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 465 - 486
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: Department of Civil and Environmental Engineering, University of Wisconsin-Madison, Madison, WI 53706, USA; Email address for correspondence: npujara@wisc.edu

References

Alyones, S. & Bruce, C. W. 2015 Electromagnetic scattering and absorption by randomly oriented fibers. J. Opt. Soc. Am. A 32, 1101–1108.Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–440.Google Scholar
Bordoloi, A. D. & Variano, E. A. 2017 Rotational kinematics of large cylindrical particles in turbulence. J. Fluid Mech. 815, 199–222.Google Scholar
Byron, M., Einarsson, J., Gustavsson, K., Voth, G., Mehlig, B. & Variano, E. 2015 Shape-dependence of particle rotation in isotropic turbulence. Phys. Fluids 27, 035101.Google Scholar
Chen, J., Jin, G. & Zhang, J. 2015 Large eddy simulation of orientation and rotation of ellipsoidal particles in isotropic turbulent flows. J. Turbul. 17, 308–326.Google Scholar
Chen, S., Sreenivasan, K. R., Nelkin, M. & Cao, N. 1997 Refined similarity hypothesis for transverse structure functions in fluid turbulence. Phys. Rev. Lett. 79, 2253–2256.Google Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11, 2394–2410.Google Scholar
Chevillard, L. & Meneveau, C. 2011 Lagrangian time correlations of vorticity alignments in isotropic turbulence: observations and model predictions. Phys. Fluids 23, 101704.Google Scholar
Chevillard, L. & Meneveau, C. 2013 Orientation dynamics of small, triaxial–ellipsoidal particles in isotropic turbulence. J. Fluid Mech. 737, 571–596.Google Scholar
Cox, R. G. 1970 The motion of long slender bodies in a viscous fluid. Part 1. General theory. J. Fluid Mech. 44, 791–810.Google Scholar
Danish, M. & Meneveau, C. 2018 Multiscale analysis of the invariants of the velocity gradient tensor in isotropic turbulence. Phys. Rev. Fluids 3, 044604.Google Scholar
Davidson, P. A. 2015 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Donzis, D. A., Yeung, P. K. & Sreenivasan, K. R. 2008 Dissipation and enstrophy in isotropic turbulence: resolution effects and scaling in direct numerical simulations. Phys. Fluids 20, 045108.Google Scholar
Dusenbery, D. B. 2009 Living at Micro Scale: The Unexpected Physics of Being Small. Harvard University Press.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Girimaji, S. S. & Pope, S. B. 1990 Material-element deformation in isotropic turbulence. J. Fluid Mech. 220, 427–458.Google Scholar
Gonzalez, O. & Stuart, A. M. 2009 A First Course in Continuum Mechanics. Cambridge University Press.Google Scholar
Guala, M., Luthi, B., Liberzon, A., Tsinober, A. & Kinzelbach, W. 2005 On the evolution of material lines and vorticity in homogeneous turbulence. J. Fluid Mech. 533, 1–21.Google Scholar
Guazzelli, É. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.Google Scholar
Gustavsson, K., Einarsson, J. & Mehlig, B. 2014 Tumbling of small axisymmetric particles in random and turbulent flows. Phys. Rev. Fluids 112, 014501.Google Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008 Direct assessment of vorticity alignment with local and nonlocal strain rates in turbulent flows. Phys. Fluids 20, 111703.Google Scholar
He, G.-W., Rubinstein, R. & Wang, L.-P. 2002 Effects of subgrid-scale modeling on time correlations in large eddy simulation. Phys. Fluids 14, 2186–2193.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Iyer, K. P., Sreenivasan, K. R. & Yeung, P. K. 2017 Reynolds number scaling of velocity increments in isotropic turbulence. Phys. Rev. E 95, 021101.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Khayat, R. E. & Cox, R. G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.Google Scholar
Kolmogorov, A. N. 1941 Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32 (1), 16–18.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Kramel, S., Voth, G. A., Tympel, S. & Toschi, F. 2016 Preferential rotation of chiral dipoles in isotropic turbulence. Phys. Rev. Lett. 117, 154501.Google Scholar
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.Google Scholar
Li, Y. & Meneveau, C. 2005 Origin of non-Gaussian statistics in hydrodynamic turbulence. Phys. Rev. Lett. 95, 164502.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9, N31.Google Scholar
Li, Y. I. & Meneveau, C. 2006 Intermittency trends and Lagrangian evolution of non-Gaussian statistics in turbulent flow and scalar transport. J. Fluid Mech. 558, 133–142.Google Scholar
Lopez, D. & Guazzelli, É. 2017 Inertial effects on fibers settling in a vortical flow. Phys. Rev. Fluids 2, 024306.Google Scholar
Lund, T. S. & Rogers, M. M. 1994 An improved measure of strain state probability in turbulent flows. Phys. Fluids 6, 1838–1847.Google Scholar
Lundell, F., Söderberg, L. D. & Alfredsson, P. H. 2011 Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 43, 195–217.Google Scholar
Luthi, B., Ott, S., Berg, J. & Mann, J. 2007 Lagrangian multi-particle statistics. J. Turbul. 8, N45.Google Scholar
Luthi, B., Tsinober, A. & Kinzelbach, W. 2005 Lagrangian measurement of vorticity dynamics in turbulent flow. J. Fluid Mech. 528, 87–118.Google Scholar
Marheineke, N. & Wegener, R. 2006 Fiber dynamics in turbulent flows: general modeling framework. SIAM J. Appl. Maths 66, 1703–1726.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.Google Scholar
Meneveau, C. & Sreenivasan, K. R. 1991 The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 224, 429–484.Google Scholar
Naso, A. & Pumir, A. 2005 Scale dependence of the coarse-grained velocity derivative tensor structure in turbulence. Phys. Rev. E 72, 056318.Google Scholar
Nelkin, M. 1999 Enstrophy and dissipation must have the same scaling exponent in the high Reynolds number limit of fluid turbulence. Phys. Fluids 11, 2202–2204.Google Scholar
Newsom, R. K. & Bruce, C. W. 1994 The dynamics of fibrous aerosols in a quiescent atmosphere. Phys. Fluids 6, 521–530.Google Scholar
Newsom, R. K. & Bruce, C. W. 1998 Orientational properties of fibrous aerosols in atmospheric turbulence. J. Aerosol. Sci. 29, 773–797.Google Scholar
Ni, R., Kramel, S., Ouellette, N. T. & Voth, G. A. 2015 Measurements of the coupling between the tumbling of rods and the velocity gradient tensor in turbulence. J. Fluid Mech. 766, 202–225.Google Scholar
Ni, R., Ouellette, N. T. & Voth, G. A. 2014 Alignment of vorticity and rods with Lagrangian fluid stretching in turbulence. J. Fluid Mech. 743, R3.Google Scholar
Niazi, A. M., Sardina, G., Brandt, L., Karp-Boss, L., Bearon, R. N. & Variano, E. A. 2017 Sedimentation of inertia-less prolate spheroids in homogenous isotropic turbulence with application to non-motile phytoplankton. J. Fluid Mech. 831, 655–674.Google Scholar
Oboukhov, A. M. 1962 Some specific features of atmospheric tubulence. J. Fluid Mech. 13, 77–81.Google Scholar
Olson, J. A. & Kerekes, R. J. 1998 The motion of fibres in turbulent flow. J. Fluid Mech. 377, 47–64.Google Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109, 134501.Google Scholar
Parsa, S. & Voth, G. A. 2014 Inertial range scaling in rotations of long rods in turbulence. Phys. Rev. Lett. 112, 024501.Google Scholar
Perlman, E., Burns, R., Li, Y. & Meneveau, C. 2007 Data exploration of turbulence simulations using a database cluster. In Supercomputing SC07. ACM, IEEE.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pruppacher, H. R. & Klett, J. D. 2012 Microphysics of Clouds and Precipitation. Springer.Google Scholar
Pujara, N., Oehmke, T. B., Bordoloi, A. D. & Variano, E. A. 2018 Rotations of large inertial cubes, cuboids, cones, and cylinders in turbulence. Phys. Rev. Fluids 3, 054605.Google Scholar
Pujara, N. & Variano, E. A. 2017 Rotations of small, inertialess triaxial ellipsoids in isotropic turbulence. J. Fluid Mech. 821, 517–538.Google Scholar
Pumir, A., Bodenschatz, E. & Xu, H. 2013 Tetrahedron deformation and alignment of perceived vorticity and strain in a turbulent flow. Phys. Fluids 25, 035101.Google Scholar
Pumir, A. & Wilkinson, M. 2011 Orientation statistics of small particles in turbulence. New J. Phys. 13, 093030.Google Scholar
Ravnik, J., Marchioli, C. & Soldati, A. 2017 Application limits of Jeffery’s theory for elongated particle torques in turbulence: a DNS assessment. Acta Mechanica 229, 827–839.Google Scholar
Shin, M. & Koch, D. L. 2005 Rotational and translational dispersion of fibres in isotropic turbulent flows. J. Fluid Mech. 540, 143–173.Google Scholar
Sinhuber, M., Bewley, G. P. & Bodenschatz, E. 2017 Dissipative effects on inertial-range statistics at high Reynolds numbers. Phys. Rev. Lett. 119, 134502.Google Scholar
Spurny, K. 2000 Atmospheric contamination by fibrous aerosols. In Aerosol Chemical Processes in the Environment. chap. 26, Lewis Publishers.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Subramanian, G. & Kock, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.Google Scholar
Voth, G. A. & Soldati, A. 2017 Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 49, 249–276.Google Scholar
Xu, H., Pumir, A. & Bodenschatz, E. 2011 The Pirouette effect in turbulent flows. Nat. Phys. 7, 709–712.Google Scholar
Yang, Y., He, G.-W. & Wang, L.-P. 2008 Effects of subgrid-scale modeling on Lagrangian statistics in large-eddy simulation. J. Turbul. 9, N8.Google Scholar
Yu, H., Kanov, K., Perlman, E., Graham, J., Frederix, E., Burns, R., Szalay, A., Eyink, G. & Meneveau, C. 2012 Studying Lagrangian dynamics of turbulence using on-demand fluid particle tracking in a public turbulence database. J. Turbul. 13, N12.Google Scholar