Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-17T09:47:06.592Z Has data issue: false hasContentIssue false
  • English
  • Français

p-adic Eisenstein-Kronecker series for CM elliptic curves and the Kronecker limit formulas

Part of: (Co)homology theory Arithmetic problems. Diophantine geometry Arithmetic algebraic geometry

Published online by Cambridge University Press:  11 January 2016

Kenichi Bannai ,
Hidekazu Furusho  and
Shinichi Kobayashi
Kenichi Bannai
Affiliation:
Department of Mathematics, Keio University, Yokohama 223-8522, Japan, bannai@math.keio.ac.jp
Hidekazu Furusho
Affiliation:
Graduate School of Mathematics, Nagoya University, Nagoya 464-8602, Japan, furusho@math.nagoya-u.ac.jp
Shinichi Kobayashi
Affiliation:
Mathematical Institute, Tohoku University, Sendai 980-8578, Japan, shinichi@math.tohoku.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider an elliptic curve defined over an imaginary quadratic field K with good reduction at the primes above p ≥ 5 and with complex multiplication by the full ring of integers 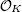of K. In this paper, we construct p-adic analogues of the Eisenstein-Kronecker series for such an elliptic curve as Coleman functions on the elliptic curve. We then prove p-adic analogues of the first and second Kronecker limit formulas by using the distribution relation of the Kronecker theta function.

MSC classification

Secondary: 11G55: Polylogarithms and relations with $K$-theory 11G07: Elliptic curves over local fields 11G15: Complex multiplication and moduli of abelian varieties 14F30: $p$-adic cohomology, crystalline cohomology 14G10: Zeta-functions and related questions (Birch-Swinnerton-Dyer conjecture)
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 219 , September 2015 , pp. 269 - 302
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2015

References

[1] Bannai, K., Rigid syntomic cohomology and p-adic polylogarithms, J. Reine Angew. Math. 529 (2000), 205–237. MR 1799937. DOI 10.1515/crll.2000.097.Google Scholar
[2] Bannai, K., On the p-adic realization of elliptic polylogarithms for CM-elliptic curves, Duke Math. J. 113 (2002), 193–236. MR 1909217. DOI 10.1215/S0012-7094-02-11321-0.CrossRefGoogle Scholar
[3] Bannai, K., Specialization of the p-adic polylogarithm to p-th power roots of unity, Doc. Math. 2003, Extra Vol., 73–97. MR 2046595.Google Scholar
[4] Bannai, K. and Kobayashi, S., “Algebraic theta functions and Eisenstein-Kronecker numbers” in Proceedings of the Symposium on Algebraic Number Theory and Related Topics, RIMS Kôkyûroku Bessatsu B4, Res. Inst. Math. Sci. (RIMS), Kyoto, 2007, 63–77. MR 2402003.Google Scholar
[5] Bannai, K., Algebraic theta functions and p-adic interpolation of Eisenstein- Kronecker numbers, Duke Math. J. 153 (2010), 229–295. MR 2667134. DOI 10.1215/00127094-2010-024.CrossRefGoogle Scholar
[6] Bannai, K., Kobayashi, S., and Tsuji, T., “Realizations of the elliptic polylogarithm for CM elliptic curves” in Algebraic Number Theory and Related Topics (2007), RIMS Kôkyûroku Bessatsu B12, Res. Inst. Math. Sci. (RIMS), Kyoto, 2009, 33–50. MR 2605771.Google Scholar
[7] Bannai, K., On the de Rham and p-adic realizations of the elliptic polylogarithm for CM elliptic curves, Ann. Sci. Éc. Norm. Supér. (4) 43 (2010), 185–234. MR 2662664.CrossRefGoogle Scholar
[8] Beilinson, A. and Levin, A., “The elliptic polylogarithm” in Motives (Seattle, 1991), Proc. Sympos. Pure Math. 55, Amer. Math. Soc., Providence, 1994, 123–190. MR 1265553.CrossRefGoogle Scholar
[9] Berthelot, P., Finitude et pureté cohomologique en cohomologie rigide, with an appendix by de Jong, A. J., Invent. Math. 128 (1997), 329–377. MR 1440308. DOI 10.1007/s002220050143.CrossRefGoogle Scholar
[10] Besser, A., “Syntomic regulators and p-adic integration, I: Rigid syntomic regulators” in Conference on p-adic Aspects of the Theory of Automorphic Representations (Jerusalem, 1998), Israel J. Math. 120, 2000, 291–334. MR 1809626. DOI 10.1007/BF02834843.Google Scholar
[11] Besser, A., “Syntomic regulators and p-adic integration, II: K 2of curves” in Conference on p-adic Aspects of the Theory of Automorphic Representations (Jerusalem, 1998), Israel J. Math. 120, 2000, 335–359. MR 1809627. DOI 10.1007/BF02834844.Google Scholar
[12] Besser, A., Coleman integration using the Tannakian formalism, Math. Ann. 322 (2002), 19–48. MR 1883387. DOI 10.1007/s002080100263.CrossRefGoogle Scholar
[13] Besser, A. and de Jeu, R., The syntomic regulator for the K-theory of fields, Ann. Sci. Éc. Norm. Supér. (4) 36 (2003), 867–924. MR 2032529. DOI 10.1016/j.ansens.2003.01.003. CrossRefGoogle Scholar
[14] Coleman, R. F., Dilogarithms, regulators and p-adic L-functions, Invent. Math. 69 (1982), 171–208. MR 0674400. DOI 10.1007/BF01399500.CrossRefGoogle Scholar
[15] Damerell, R., L-functions of elliptic curves with complex multiplication, I. Acta Arith. 17 (1970) 287–301. MR 0285540.CrossRefGoogle Scholar
[16] Damerell, R., L-functions of elliptic curves with complex multiplication, II. Acta Arith. 19 (1971), 311–317. MR 0399103.CrossRefGoogle Scholar
[17] Deligne, P., “Le groupe fondamental de la droite projective moins trois points” in Galois Groups Over ℚ (Berkeley, 1987), Math. Sci. Res. Inst. Publ. 16, Springer, New York, 1989, 79–29779-297. MR 1012168. DOI 10.1007/978-1-4613-9649-93.CrossRefGoogle Scholar
[18] de Shalit, E., Iwasawa Theory of Elliptic Curves with Complex Multiplication: p-adic L Functions, Perspect. Math. 3, Academic Press, Boston, 1987. MR 0917944. Google Scholar
[19] Furusho, H., p-adic multiple zeta values, I: p-adic multiple polylogarithms and the p-adic KZ equation, Invent. Math. 55 (2004), 253–286. MR 2031428. DOI 10.1007/s00222-003-0320-9.CrossRefGoogle Scholar
[20] Katz, N. M., p-adic interpolation of real analytic Eisenstein series, Ann. of Math. (2) 104 (1976), 459–571. MR 0506271.CrossRefGoogle Scholar
[21] Levin, A., Elliptic polylogarithms: An analytic theory, Compos. Math. 106 (1997), 267–282. MR 1457106. DOI 10.1023/A:1000193320513. CrossRefGoogle Scholar
[22] Robert, G., Unités elliptiques et formules pour le nombre de classes des extensions abéliennes d'un corps quadratique imaginaire, Mém. Soc. Math. France 36, Soc. Math. France, Paris, 1973. MR 0469889. Google Scholar
[23] Somekawa, M., Log-syntomic regulators and p-adic polylogarithms, K-Theory 17 (1999), 265–294. MR 1703301. DOI 10.1023/A:1007755726476.CrossRefGoogle Scholar
[24] Weil, A., Elliptic Functions According to Eisenstein and Kronecker, Ergeb. Math. Grenzgeb (3) 88, Springer, Berlin, 1976. MR 0562289.Google Scholar
[25] Wildeshaus, J., On an elliptic analogue of Zagier's conjecture, Duke Math. J. 87 (1997), 355–407. MR 1443532. DOI 10.1215/S0012-7094-97-08714-7. CrossRefGoogle Scholar
[26] Zagier, D., Periods of modular forms and Jacobi theta functions, Invent. Math. 104 (1991), 449–465. MR 1106744. DOI 10.1007/BF01245085.CrossRefGoogle Scholar