Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-15T12:31:54.361Z Has data issue: false hasContentIssue false
  • English
  • Français

THE HERBRAND FUNCTIONAL INTERPRETATION OF THE DOUBLE NEGATION SHIFT

Published online by Cambridge University Press:  19 June 2017

MARTÍN ESCARDÓ  and
PAULO OLIVA
MARTÍN ESCARDÓ
Affiliation:
SCHOOL OF ELECTRONIC ENGINEERING AND COMPUTER SCIENCE QUEEN MARY UNIVERSITY OF LONDON LONDON, UK E-mail: p.oliva@qmul.ac.uk
PAULO OLIVA
Affiliation:
SCHOOL OF COMPUTER SCIENCE UNIVERSITY OF BIRMINGHAM BIRMINGHAM, UKE-mail: m.escardo@cs.bham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers a generalisation of selection functions over an arbitrary strong monad T, as functionals of type 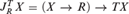$J_R^T X = (X \to R) \to TX$. It is assumed throughout that R is a T-algebra. We show that 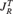$J_R^T$ is also a strong monad, and that it embeds into the continuation monad 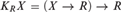$K_R X = (X \to R) \to R$. We use this to derive that the explicitly controlled product of T-selection functions is definable from the explicitly controlled product of quantifiers, and hence from Spector’s bar recursion. We then prove several properties of this product in the special case when T is the finite powerset monad 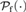${\cal P}_{\rm{f}} \left( \cdot \right)$. These are used to show that when 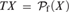$TX = {\cal P}_{\rm{f}} \left( X \right)$ the explicitly controlled product of T-selection functions calculates a witness to the Herbrand functional interpretation of the double negation shift.

Keywords

03F0703F10bar recursionHerbrand functional interpretationdialectica interpretationmonads
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 590 - 607
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berardi, S., Bezem, M., and Coquand, T., On the computational content of the axiom of choice, this Journal, vol. 63 (1998), no. 2, pp. 600–622.Google Scholar
Berger, U. and Oliva, P., Modified bar recursion. Mathematical Structures in Computer Science, vol. 16 (2006), pp. 163–183.Google Scholar
Bezem, M., Strongly majorizable functionals of finite type: A model for bar recursion containing discontinuous functionals, this Journal, vol. 50 (1985), pp. 652–660.Google Scholar
Escardó, M. and Oliva, P., Computational interpretations of analysis via products of selection functions, Computability in Europe 2010 (Ferreira, F., Lowe, B., Mayordomo, E., and Gomes, L. M., editors), Lecture Notes in Computer Science, Springer, Berlin, Heidelberg, 2010, pp. 141–150.Google Scholar
Escardó, M. and Oliva, P., Selection functions, bar recursion, and backward induction . Mathematical Structures in Computer Science, vol. 20 (2010), no. 2, pp. 127–168.CrossRefGoogle Scholar
Escardó, M. and Oliva, P., Sequential games and optimal strategies . Royal Society Proceedings A, vol. 467 (2011), pp. 1519–1545.Google Scholar
Escardó, M. and Oliva, P., Bar recursion and products of selection functions, this Journal, vol. 80 (2015), no. 1, pp. 1–28.Google Scholar
Ferreira, F. and Engrácia, P., The bounded functional interpretation of the double negation shift, this Journal, vol. 75 (2010), no. 2, pp. 759–773.Google Scholar
Ferreira, F. and Gaspar, J., Nonstandardness and the bounded functional interpretation . Annals of Pure and Applied Logic, vol. 166 (2015), pp. 665–740.Google Scholar
Gödel, K., Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes . Dialectica, vol. 12 (1958), pp. 280–287.Google Scholar
Kock, A., Strong functors and monoidal monads . Archiv der Mathematik, vol. 23 (1972), pp. 113–120.Google Scholar
Kohlenbach, U., Effective bounds from ineffective proofs in analysis: An application of functional interpretation and majorization, this Journal, vol. 57 (1992), pp. 1239–1273.Google Scholar
Moggi, E., Notions of computation and monads . Information and Computation, vol. 1 (1991), pp. 55–92.CrossRefGoogle Scholar
Mostowski, A., On a generalization of quantifiers . Fundamenta Mathematicae, vol. 44 (1957), pp. 12–36.Google Scholar
Oliva, P. and Powell, T., On Spector’s bar recursion . Mathematical Logic Quarterly, vol. 58 (2012), no. 4–5, pp. 356–365.CrossRefGoogle Scholar
Scarpellini, B., A model for bar recursion of higher types. Compositio Mathematica, vol. 23 (1971), pp. 123–153.Google Scholar
Spector, C., Provably recursive functionals of analysis: A consistency proof of analysis by an extension of principles in current intuitionistic mathematics, Recursive Function Theory: Proceedings of Symposia in Pure Mathematics, vol. 5 (Dekker, F. D. E., editor), American Mathematical Society, Providence, Rhode Island, 1962, pp. 1–27.Google Scholar
Troelstra, A. S., Metamathematical Investigation of Intuitionistic Arithmetic and Analysis, Lecture Notes in Mathematics, vol. 344, Springer, Berlin, 1973.Google Scholar
van den Berg, B., Briseid, E. M., and Safarik, P., A functional interpretation for nonstandard arithmetic . Annals of Pure and Applied Logic, vol. 163 (2012), no. 2, pp. 1962–1994.Google Scholar
Wadler, P., The essence of functional programming , Proceedings of the 19th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL’92, ACM, New York, NY, USA, 1992, pp. 1–14.Google Scholar