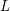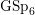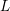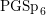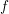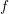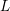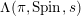1 Introduction
1.1 Main theorems
The purpose of this paper is to give a family of Rankin–Selberg integrals
 $I_{B}(\unicode[STIX]{x1D719},s)$
for the Spin
$I_{B}(\unicode[STIX]{x1D719},s)$
for the Spin
![]() $L$
-function of the cuspidal automorphic representations of
$L$
-function of the cuspidal automorphic representations of
 $\operatorname{GSp}_{6}(\mathbf{A})$
that correspond to Siegel modular forms. The Rankin–Selberg integrals are indexed by quaternion algebras
$\operatorname{GSp}_{6}(\mathbf{A})$
that correspond to Siegel modular forms. The Rankin–Selberg integrals are indexed by quaternion algebras
![]() $B$
over
$B$
over
![]() $\mathbf{Q}$
that are ramified at the infinite place.
$\mathbf{Q}$
that are ramified at the infinite place.
Denote by
![]() ${\mathcal{H}}_{3}$
the Siegel upper half-space of degree three;
${\mathcal{H}}_{3}$
the Siegel upper half-space of degree three;
![]() ${\mathcal{H}}_{3}$
is the space of
${\mathcal{H}}_{3}$
is the space of
![]() $3\times 3$
complex symmetric matrices
$3\times 3$
complex symmetric matrices
![]() $Z$
whose imaginary part is positive definite:
$Z$
whose imaginary part is positive definite:
 $$\begin{eqnarray}{\mathcal{H}}_{3}=\{Z=X+iY\in M_{3}(\mathbf{C}):\text{}^{t}Z=Z,Y>0\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{H}}_{3}=\{Z=X+iY\in M_{3}(\mathbf{C}):\text{}^{t}Z=Z,Y>0\}.\end{eqnarray}$$
Denote by
 $\operatorname{GSp}_{6}^{+}(\mathbf{R})$
the subgroup of
$\operatorname{GSp}_{6}^{+}(\mathbf{R})$
the subgroup of
 $\operatorname{GSp}_{6}(\mathbf{R})$
whose elements have positive similitude. Then
$\operatorname{GSp}_{6}(\mathbf{R})$
whose elements have positive similitude. Then
 $\operatorname{GSp}_{6}^{+}(\mathbf{R})$
acts on
$\operatorname{GSp}_{6}^{+}(\mathbf{R})$
acts on
![]() ${\mathcal{H}}_{3}$
by the formula
${\mathcal{H}}_{3}$
by the formula
 $gZ=(AZ+B)(CZ+D)^{-1}$
if
$gZ=(AZ+B)(CZ+D)^{-1}$
if
 $g=(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!)$
. Define
$g=(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!)$
. Define
 $K_{\infty ,\operatorname{Sp}_{6}}\simeq U(3)$
to be the subgroup of
$K_{\infty ,\operatorname{Sp}_{6}}\simeq U(3)$
to be the subgroup of
![]() $\operatorname{Sp}_{6}(\mathbf{R})$
that stabilizes
$\operatorname{Sp}_{6}(\mathbf{R})$
that stabilizes
![]() $i\in {\mathcal{H}}_{3}$
for this action. For
$i\in {\mathcal{H}}_{3}$
for this action. For
![]() $Z\in {\mathcal{H}}_{3}$
and
$Z\in {\mathcal{H}}_{3}$
and
 $g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
, define
$g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
, define
 $j(g,Z)=\unicode[STIX]{x1D708}(g)^{-2}\det (CZ+D)$
, where
$j(g,Z)=\unicode[STIX]{x1D708}(g)^{-2}\det (CZ+D)$
, where
![]() $\unicode[STIX]{x1D708}$
is the similitude.
$\unicode[STIX]{x1D708}$
is the similitude.
Suppose
![]() $r\geqslant 0$
is an integer, and
$r\geqslant 0$
is an integer, and
![]() $\unicode[STIX]{x1D70B}$
is a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$
is a cuspidal automorphic representation of
 $\operatorname{GSp}_{6}(\mathbf{A})$
.
$\operatorname{GSp}_{6}(\mathbf{A})$
.
Definition 1.1. We say that
![]() $\unicode[STIX]{x1D70B}$
is associated to a level-one Siegel modular form of weight
$\unicode[STIX]{x1D70B}$
is associated to a level-one Siegel modular form of weight
![]() $2r$
if the following conditions are satisfied.
$2r$
if the following conditions are satisfied.
-
– There is a nonzero
 $\unicode[STIX]{x1D719}$
in the space of
$\unicode[STIX]{x1D719}$
in the space of
 $\unicode[STIX]{x1D70B}$
satisfying
$\unicode[STIX]{x1D70B}$
satisfying
 $\unicode[STIX]{x1D719}(gk_{f}k_{\infty })=j(k_{\infty },i)^{-2r}\unicode[STIX]{x1D719}(g)$
for all
$\unicode[STIX]{x1D719}(gk_{f}k_{\infty })=j(k_{\infty },i)^{-2r}\unicode[STIX]{x1D719}(g)$
for all
 $g\in \operatorname{GSp}_{6}(\mathbf{A})$
,
$g\in \operatorname{GSp}_{6}(\mathbf{A})$
,
 $k_{f}\in \prod _{p}\operatorname{GSp}_{6}(\mathbf{Z}_{p})$
, and
$k_{f}\in \prod _{p}\operatorname{GSp}_{6}(\mathbf{Z}_{p})$
, and
 $k_{\infty }\in K_{\infty ,\operatorname{Sp}_{6}}$
.
$k_{\infty }\in K_{\infty ,\operatorname{Sp}_{6}}$
. -
–
 $\unicode[STIX]{x1D70B}$
has trivial central character.
$\unicode[STIX]{x1D70B}$
has trivial central character. -
– The function
 $f_{\unicode[STIX]{x1D719}}:{\mathcal{H}}_{3}\rightarrow \mathbf{C}$
well defined by the equality
$f_{\unicode[STIX]{x1D719}}:{\mathcal{H}}_{3}\rightarrow \mathbf{C}$
well defined by the equality
 $f_{\unicode[STIX]{x1D719}}(g_{\infty }(i))=\unicode[STIX]{x1D708}(g_{\infty })^{r}j(g_{\infty },i)^{2r}\unicode[STIX]{x1D719}(g_{\infty })$
for all
$f_{\unicode[STIX]{x1D719}}(g_{\infty }(i))=\unicode[STIX]{x1D708}(g_{\infty })^{r}j(g_{\infty },i)^{2r}\unicode[STIX]{x1D719}(g_{\infty })$
for all
 $g_{\infty }\in \operatorname{GSp}_{6}(\mathbf{R})^{+}$
is a classical Siegel modular form of weight
$g_{\infty }\in \operatorname{GSp}_{6}(\mathbf{R})^{+}$
is a classical Siegel modular form of weight
 $2r$
.
$2r$
.
See, for example, [Reference Asgari and SchmidtAS01, § 4] for more on the relationship between Siegel modular forms and their associated automorphic representations. The content of the final condition is that
![]() $f_{\unicode[STIX]{x1D719}}$
is a holomorphic function on
$f_{\unicode[STIX]{x1D719}}$
is a holomorphic function on
![]() ${\mathcal{H}}_{3}$
, and thus has a Fourier expansion of the form
${\mathcal{H}}_{3}$
, and thus has a Fourier expansion of the form
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D719}}(Z)=\mathop{\sum }_{T>0}a_{f}(T)e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(TZ)}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D719}}(Z)=\mathop{\sum }_{T>0}a_{f}(T)e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(TZ)}.\end{eqnarray}$$
Here the sum ranges over all half-integral, symmetric,
![]() $3\times 3$
matrices
$3\times 3$
matrices
![]() $T$
that are positive definite.
$T$
that are positive definite.
Via the even Clifford construction, half-integral, symmetric,
![]() $3\times 3$
matrices
$3\times 3$
matrices
![]() $T$
correspond to pairs
$T$
correspond to pairs
 $(\unicode[STIX]{x1D6EC},\{1,v_{1},v_{2},v_{3}\})$
consisting of orders
$(\unicode[STIX]{x1D6EC},\{1,v_{1},v_{2},v_{3}\})$
consisting of orders
![]() $\unicode[STIX]{x1D6EC}$
in quaternion algebras over
$\unicode[STIX]{x1D6EC}$
in quaternion algebras over
![]() $\mathbf{Q}$
equipped with a particular type of nice ordered basis
$\mathbf{Q}$
equipped with a particular type of nice ordered basis
 $\{1,v_{1},v_{2},v_{3}\}$
of
$\{1,v_{1},v_{2},v_{3}\}$
of
![]() $\unicode[STIX]{x1D6EC}$
. This correspondence goes back at least to Brzezinski [Reference BrzezińskiBrz83, Proposition 5.2], and more recently it has been studied and generalized by Gross and Lucianovic [Reference Gross and LucianovicGL09]. The condition that
$\unicode[STIX]{x1D6EC}$
. This correspondence goes back at least to Brzezinski [Reference BrzezińskiBrz83, Proposition 5.2], and more recently it has been studied and generalized by Gross and Lucianovic [Reference Gross and LucianovicGL09]. The condition that
![]() $T$
be positive (or negative) definite is exactly that the associated quaternion algebra
$T$
be positive (or negative) definite is exactly that the associated quaternion algebra
![]() $\unicode[STIX]{x1D6EC}\,\otimes \,\mathbf{Q}$
be ramified at infinity. As an example, the identity matrix
$\unicode[STIX]{x1D6EC}\,\otimes \,\mathbf{Q}$
be ramified at infinity. As an example, the identity matrix
![]() $1_{3}$
corresponds to the order
$1_{3}$
corresponds to the order
 $\mathbf{Z}+\mathbf{Z}i+\mathbf{Z}j+\mathbf{Z}k$
in Hamilton’s quaternions, while the matrix
$\mathbf{Z}+\mathbf{Z}i+\mathbf{Z}j+\mathbf{Z}k$
in Hamilton’s quaternions, while the matrix
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1 & {\textstyle \frac{1}{2}} & {\textstyle \frac{1}{2}}\\ {\textstyle \frac{1}{2}} & 1 & {\textstyle \frac{1}{2}}\\ {\textstyle \frac{1}{2}} & {\textstyle \frac{1}{2}} & 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}1 & {\textstyle \frac{1}{2}} & {\textstyle \frac{1}{2}}\\ {\textstyle \frac{1}{2}} & 1 & {\textstyle \frac{1}{2}}\\ {\textstyle \frac{1}{2}} & {\textstyle \frac{1}{2}} & 1\end{array}\right)\end{eqnarray}$$
corresponds to Hurwitz’s maximal order
 $$\begin{eqnarray}\{a+xi+yj+zk:a,x,y,z\in \mathbf{Z}~\text{or}~a,x,y,z\in \mathbf{Z}+{\textstyle \frac{1}{2}}\}.\end{eqnarray}$$
$$\begin{eqnarray}\{a+xi+yj+zk:a,x,y,z\in \mathbf{Z}~\text{or}~a,x,y,z\in \mathbf{Z}+{\textstyle \frac{1}{2}}\}.\end{eqnarray}$$
A cuspidal representation
![]() $\unicode[STIX]{x1D70B}$
that is associated to a level-one Siegel modular form is spherical at all finite places, and thus has a Spin
$\unicode[STIX]{x1D70B}$
that is associated to a level-one Siegel modular form is spherical at all finite places, and thus has a Spin
![]() $L$
-function
$L$
-function
 $L(\unicode[STIX]{x1D70B},\text{Spin},s)$
, defined for
$L(\unicode[STIX]{x1D70B},\text{Spin},s)$
, defined for
 $\text{Re}(s)\gg 0$
as an absolutely convergent Euler product over all the primes of
$\text{Re}(s)\gg 0$
as an absolutely convergent Euler product over all the primes of
![]() $\mathbf{Q}$
. If
$\mathbf{Q}$
. If
![]() $\unicode[STIX]{x1D70B}$
is associated to Siegel modular form of weight
$\unicode[STIX]{x1D70B}$
is associated to Siegel modular form of weight
![]() $2r$
, we define the completed Spin
$2r$
, we define the completed Spin
![]() $L$
-function
$L$
-function
 $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)$
to be
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)$
to be
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)=\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-2)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-1)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+3r-3)L(\unicode[STIX]{x1D70B},\text{Spin},s)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)=\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-2)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-1)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+3r-3)L(\unicode[STIX]{x1D70B},\text{Spin},s)\end{eqnarray}$$
where, as usual,
 $\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s)=2(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)$
. Our main theorem is the following.
$\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s)=2(2\unicode[STIX]{x1D70B})^{-s}\unicode[STIX]{x1D6E4}(s)$
. Our main theorem is the following.
Theorem 1.2. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$
is a cuspidal automorphic representation of
 $\operatorname{GSp}_{6}(\mathbf{A})$
associated to a level-one Siegel modular form
$\operatorname{GSp}_{6}(\mathbf{A})$
associated to a level-one Siegel modular form
![]() $f$
of weight
$f$
of weight
![]() $2r$
. Suppose furthermore that
$2r$
. Suppose furthermore that
 $a_{f}(T)\neq 0$
for some Fourier coefficient
$a_{f}(T)\neq 0$
for some Fourier coefficient
![]() $a_{f}(T)$
of
$a_{f}(T)$
of
![]() $f$
, such that
$f$
, such that
![]() $T$
corresponds to a maximal order in some quaternion algebra over
$T$
corresponds to a maximal order in some quaternion algebra over
![]() $\mathbf{Q}$
ramified at infinity. Then
$\mathbf{Q}$
ramified at infinity. Then
 $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)$
has meromorphic continuation in
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)$
has meromorphic continuation in
![]() $s$
to the entire complex plane with at worst finitely many poles, and satisfies the functional equation
$s$
to the entire complex plane with at worst finitely many poles, and satisfies the functional equation
 $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)=\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},1-s)$
.
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)=\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},1-s)$
.
The meromorphic continuation of the
![]() $L$
-function, but not the functional equation or finiteness of the poles, was known previously. Namely, the Spin
$L$
-function, but not the functional equation or finiteness of the poles, was known previously. Namely, the Spin
![]() $L$
-function on
$L$
-function on
![]() $\operatorname{GSp}_{6}$
appears in the constant term of a cuspidal Eisenstein series on an exceptional group of type
$\operatorname{GSp}_{6}$
appears in the constant term of a cuspidal Eisenstein series on an exceptional group of type
![]() $F_{4}$
. Thus its meromorphic continuation follows from the method of Langlands [Reference LanglandsLan71], see Shahidi [Reference ShahidiSha88, Theorem 6.1]. Since the underlying cuspidal representation of a Siegel modular form is not generic, the Langlands–Shahidi method cannot be used to obtain the functional equation or the finiteness of the poles of this
$F_{4}$
. Thus its meromorphic continuation follows from the method of Langlands [Reference LanglandsLan71], see Shahidi [Reference ShahidiSha88, Theorem 6.1]. Since the underlying cuspidal representation of a Siegel modular form is not generic, the Langlands–Shahidi method cannot be used to obtain the functional equation or the finiteness of the poles of this
![]() $L$
-function.
$L$
-function.
The bound we get on the poles is that they are contained in the set of integer and half-integer points in the interval
![]() $[-2,3]$
; this bound is not expected to be optimal. One should be able to get much better control of the poles by applying the theorems of Yamana [Reference YamanaYam13]. Let us also remark that it is known [Reference YamanaYam09] that every level-one Siegel modular form has a nonvanishing Fourier coefficient
$[-2,3]$
; this bound is not expected to be optimal. One should be able to get much better control of the poles by applying the theorems of Yamana [Reference YamanaYam13]. Let us also remark that it is known [Reference YamanaYam09] that every level-one Siegel modular form has a nonvanishing Fourier coefficient
![]() $a(T)$
for a
$a(T)$
for a
![]() $T$
that is primitive, meaning that
$T$
that is primitive, meaning that
![]() $T/n$
is not half-integral for all integers
$T/n$
is not half-integral for all integers
![]() $n>1$
. The primitive
$n>1$
. The primitive
![]() $T$
correspond to Gorenstein quaternion orders [Reference Gross and LucianovicGL09], the set of which strictly contain the set of maximal orders.
$T$
correspond to Gorenstein quaternion orders [Reference Gross and LucianovicGL09], the set of which strictly contain the set of maximal orders.
It is an interesting question to determine if every level-one Siegel modular form
![]() $f$
on
$f$
on
![]() $\operatorname{GSp}_{6}$
as in Theorem 1.2 has a nonvanishing Fourier coefficient
$\operatorname{GSp}_{6}$
as in Theorem 1.2 has a nonvanishing Fourier coefficient
![]() $a_{f}(T)$
with
$a_{f}(T)$
with
![]() $T$
corresponding to a maximal order. The analogous statement for Siegel modular forms on
$T$
corresponding to a maximal order. The analogous statement for Siegel modular forms on
![]() $\operatorname{GSp}_{4}$
was proved by Saha in [Reference SahaSah13]. On
$\operatorname{GSp}_{4}$
was proved by Saha in [Reference SahaSah13]. On
![]() $\operatorname{GSp}_{4}$
, Fourier coefficients
$\operatorname{GSp}_{4}$
, Fourier coefficients
![]() $a(T)$
of level-one Siegel modular forms are parametrized by
$a(T)$
of level-one Siegel modular forms are parametrized by
![]() $2\times 2$
half-integral symmetric matrices. Applying Gauss composition, such
$2\times 2$
half-integral symmetric matrices. Applying Gauss composition, such
![]() $T$
correspond to pairs
$T$
correspond to pairs
![]() $(S,I)$
where
$(S,I)$
where
![]() $S$
is a quadratic ring and
$S$
is a quadratic ring and
![]() $I$
is an ideal class for
$I$
is an ideal class for
![]() $S$
. It is a consequence of the main results of [Reference SahaSah13] that every level-one Siegel modular form on
$S$
. It is a consequence of the main results of [Reference SahaSah13] that every level-one Siegel modular form on
![]() $\operatorname{GSp}_{4}$
has a nonvanishing Fourier coefficient
$\operatorname{GSp}_{4}$
has a nonvanishing Fourier coefficient
![]() $a(T)$
for a
$a(T)$
for a
![]() $T$
that corresponds to a pair
$T$
that corresponds to a pair
![]() $(S,I)$
with
$(S,I)$
with
![]() $S$
the maximal order in a quadratic imaginary extension of
$S$
the maximal order in a quadratic imaginary extension of
![]() $\mathbf{Q}$
. Analogously to Theorem 1.2, the need for a nonvanishing ‘maximal’ Fourier coefficient for Siegel modular forms on
$\mathbf{Q}$
. Analogously to Theorem 1.2, the need for a nonvanishing ‘maximal’ Fourier coefficient for Siegel modular forms on
![]() $\operatorname{GSp}_{4}$
arises in the integral representation of Furusawa [Reference FurusawaFur93].
$\operatorname{GSp}_{4}$
arises in the integral representation of Furusawa [Reference FurusawaFur93].
Since we obtain the functional equation of the completed Spin
![]() $L$
-function for level-one Siegel modular forms, we thus get the exact order of vanishing of
$L$
-function for level-one Siegel modular forms, we thus get the exact order of vanishing of
 $L(\unicode[STIX]{x1D70B},\text{Spin},s)$
for these
$L(\unicode[STIX]{x1D70B},\text{Spin},s)$
for these
![]() $\unicode[STIX]{x1D70B}$
at sufficiently negative integers.
$\unicode[STIX]{x1D70B}$
at sufficiently negative integers.
Corollary 1.3. Suppose that
![]() $\unicode[STIX]{x1D70B}$
is a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$
is a cuspidal automorphic representation of
 $\operatorname{GSp}_{6}(\mathbf{A})$
associated to a level-one Siegel modular form
$\operatorname{GSp}_{6}(\mathbf{A})$
associated to a level-one Siegel modular form
![]() $f$
of even weight, and that
$f$
of even weight, and that
 $a_{f}(T)\neq 0$
for a Fourier coefficient of
$a_{f}(T)\neq 0$
for a Fourier coefficient of
![]() $f$
corresponding to a maximal order in a quaternion algebra over
$f$
corresponding to a maximal order in a quaternion algebra over
![]() $\mathbf{Q}$
. Then
$\mathbf{Q}$
. Then
 $\text{ord}_{s=-j}L(\unicode[STIX]{x1D70B},\text{Spin},s)=4$
for sufficiently large integers
$\text{ord}_{s=-j}L(\unicode[STIX]{x1D70B},\text{Spin},s)=4$
for sufficiently large integers
![]() $j$
.
$j$
.
Theorem 1.2 follows from the analysis of the Rankin–Selberg integral
 $I_{B}(\unicode[STIX]{x1D719},s)$
for the Spin
$I_{B}(\unicode[STIX]{x1D719},s)$
for the Spin
![]() $L$
-function, together with the analytic properties of the normalized Eisenstein series used in the integral. Suppose that
$L$
-function, together with the analytic properties of the normalized Eisenstein series used in the integral. Suppose that
![]() $B$
is a quaternion algebra over
$B$
is a quaternion algebra over
![]() $\mathbf{Q}$
, ramified at infinity. Denote by
$\mathbf{Q}$
, ramified at infinity. Denote by
![]() $J$
the set of
$J$
the set of
![]() $3\times 3$
Hermitian matrices over
$3\times 3$
Hermitian matrices over
![]() $B$
:
$B$
:
 $J=\{h\in M_{3}(B):h^{\ast }=h\}$
, where for
$J=\{h\in M_{3}(B):h^{\ast }=h\}$
, where for
 $x\in M_{3}(B)$
,
$x\in M_{3}(B)$
,
![]() $x^{\ast }$
denotes the transpose conjugate of
$x^{\ast }$
denotes the transpose conjugate of
![]() $x$
, the conjugation being from the quaternion structure on
$x$
, the conjugation being from the quaternion structure on
![]() $B$
. Associated to
$B$
. Associated to
![]() $J$
, the Freudenthal construction produces a reductive
$J$
, the Freudenthal construction produces a reductive
![]() $\mathbf{Q}$
-group
$\mathbf{Q}$
-group
![]() $\text{G}$
of type
$\text{G}$
of type
![]() $D_{6}$
, and there is an embedding
$D_{6}$
, and there is an embedding
 $\operatorname{GSp}_{6}\rightarrow \text{G}$
. The group
$\operatorname{GSp}_{6}\rightarrow \text{G}$
. The group
![]() $\text{G}$
has a maximal parabolic
$\text{G}$
has a maximal parabolic
![]() $P$
, whose unipotent radical is abelian, and naturally isomorphic to
$P$
, whose unipotent radical is abelian, and naturally isomorphic to
![]() $J$
under addition. Suppose
$J$
under addition. Suppose
![]() $r\geqslant 0$
is an integer, and
$r\geqslant 0$
is an integer, and
![]() $B_{0}$
is a maximal order in
$B_{0}$
is a maximal order in
![]() $B$
. Associated to
$B$
. Associated to
![]() $r,B_{0}$
, and a character
$r,B_{0}$
, and a character
 $\unicode[STIX]{x1D712}_{s}:P(\mathbf{A})\rightarrow \mathbf{C}^{\times }$
, we define a normalized Eisenstein series
$\unicode[STIX]{x1D712}_{s}:P(\mathbf{A})\rightarrow \mathbf{C}^{\times }$
, we define a normalized Eisenstein series
 $E_{2r}^{\ast }(g,s)$
for
$E_{2r}^{\ast }(g,s)$
for
![]() $\text{G}$
.
$\text{G}$
.
For a cusp form
![]() $\unicode[STIX]{x1D719}$
in the space of a cuspidal representation
$\unicode[STIX]{x1D719}$
in the space of a cuspidal representation
![]() $\unicode[STIX]{x1D70B}$
associated to a Siegel modular form of weight
$\unicode[STIX]{x1D70B}$
associated to a Siegel modular form of weight
![]() $2r$
, the Rankin–Selberg integral is
$2r$
, the Rankin–Selberg integral is
 $$\begin{eqnarray}I_{2r}(\unicode[STIX]{x1D719},s)=\int _{\operatorname{GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)E_{2r}^{\ast }(g,s)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}I_{2r}(\unicode[STIX]{x1D719},s)=\int _{\operatorname{GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)E_{2r}^{\ast }(g,s)\,dg.\end{eqnarray}$$
Suppose that the maximal order
![]() $B_{0}$
corresponds to the half-integral symmetric matrix
$B_{0}$
corresponds to the half-integral symmetric matrix
![]() $T$
. When
$T$
. When
![]() $\unicode[STIX]{x1D719}$
is as in Definition 1.1, we show that
$\unicode[STIX]{x1D719}$
is as in Definition 1.1, we show that
 $I_{2r}(\unicode[STIX]{x1D719},s)$
is equal to
$I_{2r}(\unicode[STIX]{x1D719},s)$
is equal to
 $a_{f_{\unicode[STIX]{x1D719}}}(T)\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s-2)$
, up to a nonzero constant. To show this equality, we unfold the integral
$a_{f_{\unicode[STIX]{x1D719}}}(T)\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s-2)$
, up to a nonzero constant. To show this equality, we unfold the integral
 $I_{2r}(\unicode[STIX]{x1D719},s)$
, and then apply the result [Reference EvdokimovEvd84] of Evdokimov, who computed a Dirichlet series for the Spin
$I_{2r}(\unicode[STIX]{x1D719},s)$
, and then apply the result [Reference EvdokimovEvd84] of Evdokimov, who computed a Dirichlet series for the Spin
![]() $L$
-function on
$L$
-function on
![]() $\operatorname{GSp}_{6}$
. More precisely, [Reference EvdokimovEvd84, Theorem 3] is not quite a Dirichlet series for the Spin
$\operatorname{GSp}_{6}$
. More precisely, [Reference EvdokimovEvd84, Theorem 3] is not quite a Dirichlet series for the Spin
![]() $L$
-function. However, when one combines [Reference EvdokimovEvd84, Theorem 3] with Lemma 3.8 below, which involves the arithmetic invariant theory of quaternion orders, and the fact that
$L$
-function. However, when one combines [Reference EvdokimovEvd84, Theorem 3] with Lemma 3.8 below, which involves the arithmetic invariant theory of quaternion orders, and the fact that
![]() $B_{0}$
is a maximal order, one does obtain a Dirichlet series for the Spin
$B_{0}$
is a maximal order, one does obtain a Dirichlet series for the Spin
![]() $L$
-function. The integral
$L$
-function. The integral
 $I_{2r}(\unicode[STIX]{x1D719},s)$
then unfolds to exactly this Dirichlet series.
$I_{2r}(\unicode[STIX]{x1D719},s)$
then unfolds to exactly this Dirichlet series.
In § 7, we use Langlands’ theorem of the constant term and functional equation, together with Maass–Shimura differential operators, to analyze the analytic properties of the normalized Eisenstein series
 $E_{2r}^{\ast }(g,s)$
. We prove that it satisfies the functional equation
$E_{2r}^{\ast }(g,s)$
. We prove that it satisfies the functional equation
 $E_{2r}^{\ast }(g,s)=E_{2r}^{\ast }(g,5-s)$
and has at most finitely many poles, all contained in the set of integral and half-integral points in the interval
$E_{2r}^{\ast }(g,s)=E_{2r}^{\ast }(g,5-s)$
and has at most finitely many poles, all contained in the set of integral and half-integral points in the interval
![]() $[0,5]$
. Theorem 1.2 then follows.
$[0,5]$
. Theorem 1.2 then follows.
1.2 The Spin
 $L$
-function
$L$
-function
When a reductive
![]() $\mathbf{Q}$
-group has an associated Shimura variety, the minuscule cocharacter
$\mathbf{Q}$
-group has an associated Shimura variety, the minuscule cocharacter
![]() $\unicode[STIX]{x1D707}$
that is part of the Shimura datum singles out a representation of the Langlands dual group, and thus an automorphic
$\unicode[STIX]{x1D707}$
that is part of the Shimura datum singles out a representation of the Langlands dual group, and thus an automorphic
![]() $L$
-function, that is of particular importance. These
$L$
-function, that is of particular importance. These
![]() $L$
-functions are expected to control the arithmetic of the Shimura variety. On Siegel modular varieties this is the Spin
$L$
-functions are expected to control the arithmetic of the Shimura variety. On Siegel modular varieties this is the Spin
![]() $L$
-function. For Siegel modular forms on
$L$
-function. For Siegel modular forms on
![]() $\operatorname{GSp}_{4}$
, the desired analytic properties of this
$\operatorname{GSp}_{4}$
, the desired analytic properties of this
![]() $L$
-function were first worked out by Andrianov [Reference AndrianovAnd71, Reference AndrianovAnd74]. Other Rankin–Selberg integrals for spinor
$L$
-function were first worked out by Andrianov [Reference AndrianovAnd71, Reference AndrianovAnd74]. Other Rankin–Selberg integrals for spinor
![]() $L$
-functions that apply to holomorphic modular forms are the triple product of Garrett [Reference GarrettGar87] on
$L$
-functions that apply to holomorphic modular forms are the triple product of Garrett [Reference GarrettGar87] on
 $\operatorname{GL}_{2}\times \operatorname{GL}_{2}\times \operatorname{GL}_{2}$
, which was extended to
$\operatorname{GL}_{2}\times \operatorname{GL}_{2}\times \operatorname{GL}_{2}$
, which was extended to
![]() $\operatorname{GL}_{2}$
over a general étale cubic algebra by Piatetski-Shapiro and Rallis [Reference Piatetski-Shapiro and RallisPSR87], and the integral of Furusawa [Reference FurusawaFur93] for the Spin
$\operatorname{GL}_{2}$
over a general étale cubic algebra by Piatetski-Shapiro and Rallis [Reference Piatetski-Shapiro and RallisPSR87], and the integral of Furusawa [Reference FurusawaFur93] for the Spin
![]() $L$
-function on
$L$
-function on
 $\operatorname{GSp}_{4}\times \operatorname{GU}(1,1)$
. The Spin
$\operatorname{GSp}_{4}\times \operatorname{GU}(1,1)$
. The Spin
![]() $L$
-function of Siegel modular forms on
$L$
-function of Siegel modular forms on
![]() $\operatorname{GSp}_{2n}$
for
$\operatorname{GSp}_{2n}$
for
![]() $n>3$
remains poorly understood.
$n>3$
remains poorly understood.
For the Spin
![]() $L$
-function on
$L$
-function on
![]() $\operatorname{GSp}_{6}$
, there is also the integral of Bump and Ginzburg [Reference Bump and GinzburgBG92] that applies to generic cusp forms, and more recently the result [Reference Pollack and ShahPS15] of Pollack and Shah that applies to cuspidal representations that support a rank-two Fourier coefficient. The integrals in [Reference Bump and GinzburgBG92] and [Reference Pollack and ShahPS15] vanish identically for holomorphic Siegel modular forms.
$\operatorname{GSp}_{6}$
, there is also the integral of Bump and Ginzburg [Reference Bump and GinzburgBG92] that applies to generic cusp forms, and more recently the result [Reference Pollack and ShahPS15] of Pollack and Shah that applies to cuspidal representations that support a rank-two Fourier coefficient. The integrals in [Reference Bump and GinzburgBG92] and [Reference Pollack and ShahPS15] vanish identically for holomorphic Siegel modular forms.
It turns out that the integral in this paper, and the older integrals [Reference GarrettGar87, Reference Piatetski-Shapiro and RallisPSR87, Reference FurusawaFur93, Reference Bump and GinzburgBG92], and [Reference Pollack and ShahPS15] all appear to be mysteriously connected to the magic triangle of Deligne and Gross [Reference Deligne and GrossDG02], as we explain in Appendix B. This connection seems to be closely related to the so-called towers of Rankin–Selberg integrals introduced by Ginzburg and Rallis [Reference Ginzburg and RallisGR94]. Furthermore, that Freudenthal’s magic square might be connected to the Rankin–Selberg method is discussed, from a perspective different from our own, in [Reference BumpBum05]. Nevertheless, we hope the examples we discuss in the appendix will stimulate future inquiry.
1.3 Layout of paper
The contents of the paper is as follows. In § 2 we review the Freudenthal construction. In § 3, we review and slightly extend the results of [Reference Gross and LucianovicGL09] that relate ternary quadratic forms and quaternion orders. In § 4, we recall [Reference EvdokimovEvd84, Theorem 3] of Evdokimov, and combine this result with the work of § 3 to obtain a Dirichlet series for the Spin
![]() $L$
-function. We define the global Rankin–Selberg integral and unfold it in § 5. In §6 we evaluate the unfolded integral in terms of
$L$
-function. We define the global Rankin–Selberg integral and unfold it in § 5. In §6 we evaluate the unfolded integral in terms of
 $\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)$
. We give some results on the group
$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)$
. We give some results on the group
![]() $\text{G}(\mathbf{A})$
and analyze the normalized Eisenstein series
$\text{G}(\mathbf{A})$
and analyze the normalized Eisenstein series
 $E_{2r}^{\ast }(g,s)$
in §7. The group
$E_{2r}^{\ast }(g,s)$
in §7. The group
![]() $\text{G}$
is closely related to a classical group
$\text{G}$
is closely related to a classical group
 $\operatorname{GU}_{6}(B)$
. In Appendix A we make this relationship explicit. In Appendix B we briefly discuss the magic triangle of Deligne and Gross and its connection to some Rankin–Selberg integrals.
$\operatorname{GU}_{6}(B)$
. In Appendix A we make this relationship explicit. In Appendix B we briefly discuss the magic triangle of Deligne and Gross and its connection to some Rankin–Selberg integrals.
2 The Freudenthal construction
In this section we review the Freudenthal construction [Reference FreudenthalFre54], specialized to the case of interest for us. Nothing in this section is new. We follow the exposition of Bhargava and Ho [Reference Bhargava and HoBH16, §§ 5.3 and 6.4] fairly closely, with the exception of our definition of rank-one elements. The reader is also instructed to see Springer [Reference SpringerSpr06] and the references contained therein for more on the Freudenthal construction.
2.1 Three-by-three hermitian matrices
Suppose that
![]() $B$
is a quaternion algebra over the ground field
$B$
is a quaternion algebra over the ground field
![]() $F$
of characteristic zero. For
$F$
of characteristic zero. For
![]() $a\in B$
, write
$a\in B$
, write
![]() $a^{\ast }$
for the conjugate of
$a^{\ast }$
for the conjugate of
![]() $a$
,
$a$
,
 $\operatorname{tr}(a)=a+a^{\ast }$
,
$\operatorname{tr}(a)=a+a^{\ast }$
,
 $n(a)=aa^{\ast }$
, the trace and norm of
$n(a)=aa^{\ast }$
, the trace and norm of
![]() $a$
. These are considered as elements of
$a$
. These are considered as elements of
![]() $F$
. The symmetric pairing on
$F$
. The symmetric pairing on
![]() $B$
is defined by
$B$
is defined by
 $$\begin{eqnarray}(u,v)=\operatorname{tr}(uv^{\ast })=(v,u).\end{eqnarray}$$
$$\begin{eqnarray}(u,v)=\operatorname{tr}(uv^{\ast })=(v,u).\end{eqnarray}$$
We consider
![]() $3\times 3$
hermitian matrices over
$3\times 3$
hermitian matrices over
![]() $B$
. If
$B$
. If
![]() $h$
is such a matrix, then
$h$
is such a matrix, then
 $$\begin{eqnarray}h=\left(\begin{array}{@{}ccc@{}}c_{1} & a_{3} & a_{2}^{\ast }\\ a_{3}^{\ast } & c_{2} & a_{1}\\ a_{2} & a_{1}^{\ast } & c_{3}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}h=\left(\begin{array}{@{}ccc@{}}c_{1} & a_{3} & a_{2}^{\ast }\\ a_{3}^{\ast } & c_{2} & a_{1}\\ a_{2} & a_{1}^{\ast } & c_{3}\end{array}\right)\end{eqnarray}$$
where
 $c_{1},c_{2},c_{3}$
are elements of
$c_{1},c_{2},c_{3}$
are elements of
![]() $F$
and
$F$
and
 $a_{1},a_{2},a_{3}$
are elements of
$a_{1},a_{2},a_{3}$
are elements of
![]() $B$
. The set of such matrices is denoted
$B$
. The set of such matrices is denoted
![]() $H_{3}(B)$
.
$H_{3}(B)$
.
For
![]() $h$
as in (2.2), define
$h$
as in (2.2), define
 $$\begin{eqnarray}N(h):=c_{1}c_{2}c_{3}-c_{1}n(a_{1})-c_{2}n(a_{2})-c_{3}n(a_{3})+\operatorname{tr}(a_{1}a_{2}a_{3})\end{eqnarray}$$
$$\begin{eqnarray}N(h):=c_{1}c_{2}c_{3}-c_{1}n(a_{1})-c_{2}n(a_{2})-c_{3}n(a_{3})+\operatorname{tr}(a_{1}a_{2}a_{3})\end{eqnarray}$$
the norm of
![]() $h$
, and
$h$
, and
 $$\begin{eqnarray}\operatorname{tr}(h)=c_{1}+c_{2}+c_{3}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{tr}(h)=c_{1}+c_{2}+c_{3}\end{eqnarray}$$
the trace of
![]() $h$
. Also define
$h$
. Also define
 $$\begin{eqnarray}h^{\#}:=\left(\begin{array}{@{}ccc@{}}c_{2}c_{3}-n(a_{1}) & a_{2}^{\ast }a_{1}^{\ast }-c_{3}a_{3} & a_{3}a_{1}-c_{2}a_{2}^{\ast }\\ a_{1}a_{2}-c_{3}a_{3}^{\ast } & c_{1}c_{3}-n(a_{2}) & a_{3}^{\ast }a_{2}^{\ast }-c_{1}a_{1}\\ a_{1}^{\ast }a_{3}^{\ast }-c_{2}a_{2} & a_{2}a_{3}-c_{1}a_{1}^{\ast } & c_{1}c_{2}-n(a_{3})\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}h^{\#}:=\left(\begin{array}{@{}ccc@{}}c_{2}c_{3}-n(a_{1}) & a_{2}^{\ast }a_{1}^{\ast }-c_{3}a_{3} & a_{3}a_{1}-c_{2}a_{2}^{\ast }\\ a_{1}a_{2}-c_{3}a_{3}^{\ast } & c_{1}c_{3}-n(a_{2}) & a_{3}^{\ast }a_{2}^{\ast }-c_{1}a_{1}\\ a_{1}^{\ast }a_{3}^{\ast }-c_{2}a_{2} & a_{2}a_{3}-c_{1}a_{1}^{\ast } & c_{1}c_{2}-n(a_{3})\end{array}\right).\end{eqnarray}$$
One has that
 $hh^{\#}=N(h)1_{3}=h^{\#}h$
, and
$hh^{\#}=N(h)1_{3}=h^{\#}h$
, and
 $(h^{\#})^{\#}=N(h)h$
.
$(h^{\#})^{\#}=N(h)h$
.
Definition 2.1. An element
 $h\in H_{3}(B)$
is said to be of rank three if
$h\in H_{3}(B)$
is said to be of rank three if
 $N(h)\neq 0$
, of rank two if
$N(h)\neq 0$
, of rank two if
 $N(h)=0$
but
$N(h)=0$
but
![]() $h^{\#}\neq 0$
, and of rank one if
$h^{\#}\neq 0$
, and of rank one if
![]() $h^{\#}=0$
but
$h^{\#}=0$
but
![]() $h\neq 0$
.
$h\neq 0$
.
For
![]() $x,y$
$x,y$
![]() $3\times 3$
hermitian matrices over
$3\times 3$
hermitian matrices over
![]() $B$
, define
$B$
, define
 $$\begin{eqnarray}x\times y:=(x+y)^{\#}-x^{\#}-y^{\#}\end{eqnarray}$$
$$\begin{eqnarray}x\times y:=(x+y)^{\#}-x^{\#}-y^{\#}\end{eqnarray}$$
and
 $$\begin{eqnarray}\operatorname{tr}(x,y):={\textstyle \frac{1}{2}}\operatorname{tr}(xy+yx).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{tr}(x,y):={\textstyle \frac{1}{2}}\operatorname{tr}(xy+yx).\end{eqnarray}$$
Finally, denote by
 $$\begin{eqnarray}(\;,\;,\;):H_{3}(B)\times H_{3}(B)\times H_{3}(B)\rightarrow F\end{eqnarray}$$
$$\begin{eqnarray}(\;,\;,\;):H_{3}(B)\times H_{3}(B)\times H_{3}(B)\rightarrow F\end{eqnarray}$$
the unique symmetric trilinear form satisfying
 $(x,x,x)=6N(x)$
. Equivalently,
$(x,x,x)=6N(x)$
. Equivalently,
 $$\begin{eqnarray}(x,y,z)=N(x+y+z)-N(x+y)-N(x+z)-N(y+z)+N(x)+N(y)+N(z).\end{eqnarray}$$
$$\begin{eqnarray}(x,y,z)=N(x+y+z)-N(x+y)-N(x+z)-N(y+z)+N(x)+N(y)+N(z).\end{eqnarray}$$
For
 $x,y,z\in H_{3}(B)$
, one has
$x,y,z\in H_{3}(B)$
, one has
 $$\begin{eqnarray}\operatorname{tr}(x\times y,z)=(x,y,z)=\operatorname{tr}(x,y\times z).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{tr}(x\times y,z)=(x,y,z)=\operatorname{tr}(x,y\times z).\end{eqnarray}$$
The trilinear form is nondegenerate in the sense that if
 $(x,y,z)=0$
for all
$(x,y,z)=0$
for all
![]() $x,y$
, then
$x,y$
, then
![]() $z=0$
. The formula
$z=0$
. The formula
 $$\begin{eqnarray}\operatorname{tr}(x,y)=\mathop{\sum }_{1\leqslant i\leqslant 3}x_{ii}y_{ii}+\mathop{\sum }_{1\leqslant i<j\leqslant 3}(x_{ij},y_{ij})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{tr}(x,y)=\mathop{\sum }_{1\leqslant i\leqslant 3}x_{ii}y_{ii}+\mathop{\sum }_{1\leqslant i<j\leqslant 3}(x_{ij},y_{ij})\end{eqnarray}$$
shows that the bilinear form
![]() $\operatorname{tr}(\;,\;)$
is nondegenerate. Here
$\operatorname{tr}(\;,\;)$
is nondegenerate. Here
![]() $x_{ij}$
denotes the
$x_{ij}$
denotes the
![]() $i,j$
entry of
$i,j$
entry of
![]() $x$
, and
$x$
, and
![]() $(\;,\;)$
is the symmetric pairing on
$(\;,\;)$
is the symmetric pairing on
![]() $B$
defined in (2.1). For
$B$
defined in (2.1). For
 $x,y\in H_{3}(B)$
, one has the formula
$x,y\in H_{3}(B)$
, one has the formula
 $$\begin{eqnarray}N(x+y)=N(x)+\operatorname{tr}(x^{\#},y)+\operatorname{tr}(x,y^{\#})+N(y).\end{eqnarray}$$
$$\begin{eqnarray}N(x+y)=N(x)+\operatorname{tr}(x^{\#},y)+\operatorname{tr}(x,y^{\#})+N(y).\end{eqnarray}$$
2.2 The defining representation
Fix the quaternion algebra
![]() $B$
over
$B$
over
![]() $F$
. We denote by
$F$
. We denote by
![]() $W$
the vector space
$W$
the vector space
 $F\oplus H_{3}(B)\oplus H_{3}(B)\oplus F$
. Typical elements of
$F\oplus H_{3}(B)\oplus H_{3}(B)\oplus F$
. Typical elements of
![]() $W$
are denoted
$W$
are denoted
 $(a,b,c,d)$
with
$(a,b,c,d)$
with
 $a,d\in F$
,
$a,d\in F$
,
 $b,c\in H_{3}(B)$
. The space
$b,c\in H_{3}(B)$
. The space
![]() $W$
is equipped with a symplectic and quartic form. The symplectic form
$W$
is equipped with a symplectic and quartic form. The symplectic form
 $\langle \;,\;\rangle :W\times W\rightarrow F$
is defined by
$\langle \;,\;\rangle :W\times W\rightarrow F$
is defined by
 $$\begin{eqnarray}\langle (a,b,c,d),(a^{\prime },b^{\prime },c^{\prime },d^{\prime })\rangle =ad^{\prime }-\operatorname{tr}(b,c^{\prime })+\operatorname{tr}(c,b^{\prime })-da^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\langle (a,b,c,d),(a^{\prime },b^{\prime },c^{\prime },d^{\prime })\rangle =ad^{\prime }-\operatorname{tr}(b,c^{\prime })+\operatorname{tr}(c,b^{\prime })-da^{\prime }.\end{eqnarray}$$
The quartic form
 $Q:W\rightarrow F$
is defined by
$Q:W\rightarrow F$
is defined by
 $$\begin{eqnarray}Q((a,b,c,d))=(ad-\operatorname{tr}(b,c))^{2}+4aN(c)+4dN(b)-4\operatorname{tr}(b^{\#},c^{\#}).\end{eqnarray}$$
$$\begin{eqnarray}Q((a,b,c,d))=(ad-\operatorname{tr}(b,c))^{2}+4aN(c)+4dN(b)-4\operatorname{tr}(b^{\#},c^{\#}).\end{eqnarray}$$
We now define the (similitude) algebraic group
![]() $\text{G}$
.
$\text{G}$
.
Definition 2.2. Consider
![]() $\operatorname{GL}(W)$
to act on the right of
$\operatorname{GL}(W)$
to act on the right of
![]() $W$
. The group
$W$
. The group
![]() $\text{G}$
is defined to be the set of
$\text{G}$
is defined to be the set of
 $(g,\unicode[STIX]{x1D708}(g))\in \operatorname{GL}(W)\times \operatorname{GL}_{1}$
that satisfy
$(g,\unicode[STIX]{x1D708}(g))\in \operatorname{GL}(W)\times \operatorname{GL}_{1}$
that satisfy
 $\langle ug,vg\rangle =\unicode[STIX]{x1D708}(g)\langle u,v\rangle$
and
$\langle ug,vg\rangle =\unicode[STIX]{x1D708}(g)\langle u,v\rangle$
and
 $Q(wg)=\unicode[STIX]{x1D708}(g)^{2}Q(w)$
for all
$Q(wg)=\unicode[STIX]{x1D708}(g)^{2}Q(w)$
for all
 $u,v,w\in W$
. The map
$u,v,w\in W$
. The map
 $\unicode[STIX]{x1D708}:\text{G}\rightarrow \operatorname{GL}_{1}$
sending
$\unicode[STIX]{x1D708}:\text{G}\rightarrow \operatorname{GL}_{1}$
sending
 $g\mapsto \unicode[STIX]{x1D708}(g)$
is called the similitude.
$g\mapsto \unicode[STIX]{x1D708}(g)$
is called the similitude.
Typically, the Freudenthal construction defines the subgroup of
![]() $\text{G}$
with similitude 1, but we will need this similitude version. It is clear that
$\text{G}$
with similitude 1, but we will need this similitude version. It is clear that
![]() $\text{G}$
is a reductive group; knowledge of the generators of
$\text{G}$
is a reductive group; knowledge of the generators of
![]() $\text{G}$
proves that it is connected as well [Reference BrownBro69].
$\text{G}$
proves that it is connected as well [Reference BrownBro69].
We will give some explicit elements of
![]() $\text{G}$
. Most simply, we have the following maps:
$\text{G}$
. Most simply, we have the following maps:
-
– for
 $\unicode[STIX]{x1D706}\in \operatorname{GL}_{1}$
,
$\unicode[STIX]{x1D706}\in \operatorname{GL}_{1}$
,
 $(a,b,c,d)\mapsto (\unicode[STIX]{x1D706}a,\unicode[STIX]{x1D706}b,\unicode[STIX]{x1D706}c,\unicode[STIX]{x1D706}d)$
, with similitude
$(a,b,c,d)\mapsto (\unicode[STIX]{x1D706}a,\unicode[STIX]{x1D706}b,\unicode[STIX]{x1D706}c,\unicode[STIX]{x1D706}d)$
, with similitude
 $\unicode[STIX]{x1D706}^{2}$
;
$\unicode[STIX]{x1D706}^{2}$
; -
– and
 $(a,b,c,d)\mapsto (\unicode[STIX]{x1D706}^{2}a,\unicode[STIX]{x1D706}b,c,\unicode[STIX]{x1D706}^{-1}d)$
, with similitude
$(a,b,c,d)\mapsto (\unicode[STIX]{x1D706}^{2}a,\unicode[STIX]{x1D706}b,c,\unicode[STIX]{x1D706}^{-1}d)$
, with similitude
 $\unicode[STIX]{x1D706}$
;
$\unicode[STIX]{x1D706}$
; -
–
 $(a,b,c,d)\mapsto (-d,c,-b,a)$
with similitude 1.
$(a,b,c,d)\mapsto (-d,c,-b,a)$
with similitude 1.
This last map we denote by
![]() $J_{6}$
, or
$J_{6}$
, or
![]() $J$
, if no confusion seems likely. Under the map
$J$
, if no confusion seems likely. Under the map
 $\operatorname{GSp}_{6}\rightarrow \text{G}$
defined in § 5.1,
$\operatorname{GSp}_{6}\rightarrow \text{G}$
defined in § 5.1,
![]() $J_{6}$
is the image of the element
$J_{6}$
is the image of the element
![]() $(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!)$
of
$(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!)$
of
![]() $\operatorname{GSp}_{6}$
.
$\operatorname{GSp}_{6}$
.
Here are some more interesting elements of
![]() $\text{G}$
. First, for
$\text{G}$
. First, for
 $X\in H_{3}(B)$
, define
$X\in H_{3}(B)$
, define
 $n(X):W\rightarrow W$
via the formula
$n(X):W\rightarrow W$
via the formula
 $$\begin{eqnarray}(a,b,c,d)n(X)=(a,b+aX,c+b\times X+aX^{\#},d+\operatorname{tr}(c,X)+\operatorname{tr}(b,X^{\#})+aN(X)).\end{eqnarray}$$
$$\begin{eqnarray}(a,b,c,d)n(X)=(a,b+aX,c+b\times X+aX^{\#},d+\operatorname{tr}(c,X)+\operatorname{tr}(b,X^{\#})+aN(X)).\end{eqnarray}$$
Similarly, for
 $Y\in H_{3}(B)$
, define
$Y\in H_{3}(B)$
, define
 $\bar{n}(Y):W\rightarrow W$
via the formula
$\bar{n}(Y):W\rightarrow W$
via the formula
 $$\begin{eqnarray}(a,b,c,d)\bar{n}(Y)=(a+\operatorname{tr}(b,Y)+\operatorname{tr}(c,Y^{\#})+dN(Y),b+c\times Y+dY^{\#},c+dY,d).\end{eqnarray}$$
$$\begin{eqnarray}(a,b,c,d)\bar{n}(Y)=(a+\operatorname{tr}(b,Y)+\operatorname{tr}(c,Y^{\#})+dN(Y),b+c\times Y+dY^{\#},c+dY,d).\end{eqnarray}$$
The following lemma says that the
 $n(X),\bar{n}(Y)$
are elements of
$n(X),\bar{n}(Y)$
are elements of
![]() $\text{G}$
with similitude 1, that
$\text{G}$
with similitude 1, that
 $n(X_{1}+X_{2})=n(X_{1})n(X_{2})$
, and similarly for
$n(X_{1}+X_{2})=n(X_{1})n(X_{2})$
, and similarly for
![]() $\bar{n}$
. For a proof of the lemma, see [Reference SpringerSpr06, Lemma 2.3].
$\bar{n}$
. For a proof of the lemma, see [Reference SpringerSpr06, Lemma 2.3].
Lemma 2.3. The maps
 $X\mapsto (n(X),1)$
and
$X\mapsto (n(X),1)$
and
 $Y\mapsto (\bar{n}(Y),1)$
define group homomorphisms
$Y\mapsto (\bar{n}(Y),1)$
define group homomorphisms
 $H_{3}(B)\rightarrow \text{G}$
.
$H_{3}(B)\rightarrow \text{G}$
.
We define one more type of (fairly) explicit element of
![]() $\text{G}$
. Consider triples
$\text{G}$
. Consider triples
 $$\begin{eqnarray}(t,\tilde{t},\unicode[STIX]{x1D706})\in \operatorname{GL}(H_{3}(B))\times \operatorname{GL}(H_{3}(B))\times \operatorname{GL}_{1}\end{eqnarray}$$
$$\begin{eqnarray}(t,\tilde{t},\unicode[STIX]{x1D706})\in \operatorname{GL}(H_{3}(B))\times \operatorname{GL}(H_{3}(B))\times \operatorname{GL}_{1}\end{eqnarray}$$
that satisfy, for all
 $b,c\in H_{3}(B)$
:
$b,c\in H_{3}(B)$
:
-
–
 $\operatorname{tr}(t(b),\tilde{t}(c))=\operatorname{tr}(b,c)$
;
$\operatorname{tr}(t(b),\tilde{t}(c))=\operatorname{tr}(b,c)$
; -
–
 $N(t(b))=\unicode[STIX]{x1D706}N(b)$
;
$N(t(b))=\unicode[STIX]{x1D706}N(b)$
; -
–
 $N(\tilde{t}(c))=\unicode[STIX]{x1D706}^{-1}N(c)$
;
$N(\tilde{t}(c))=\unicode[STIX]{x1D706}^{-1}N(c)$
; -
–
 $t(b)^{\#}=\unicode[STIX]{x1D706}\tilde{t}(b^{\#})$
and
$t(b)^{\#}=\unicode[STIX]{x1D706}\tilde{t}(b^{\#})$
and
 $\tilde{t}(c)^{\#}=\unicode[STIX]{x1D706}^{-1}t(c^{\#})$
.
$\tilde{t}(c)^{\#}=\unicode[STIX]{x1D706}^{-1}t(c^{\#})$
.
Since the pairing
![]() $\operatorname{tr}(\;,\;)$
is nondegenerate, the first property uniquely determines
$\operatorname{tr}(\;,\;)$
is nondegenerate, the first property uniquely determines
![]() $\tilde{t}$
in terms of
$\tilde{t}$
in terms of
![]() $t$
, and then the first two properties imply the final two. If
$t$
, and then the first two properties imply the final two. If
 $m\in \operatorname{GL}_{3}(B)$
, and
$m\in \operatorname{GL}_{3}(B)$
, and
 $r\in \operatorname{GL}_{1}(F)$
, then the linear map
$r\in \operatorname{GL}_{1}(F)$
, then the linear map
 $t(b)=r^{-1}m^{\ast }bm$
satisfies
$t(b)=r^{-1}m^{\ast }bm$
satisfies
 $N(t(b))=r^{-3}N(m^{\ast }m)N(b)$
for all
$N(t(b))=r^{-3}N(m^{\ast }m)N(b)$
for all
![]() $b$
in
$b$
in
![]() $H_{3}(B)$
, and thus defines such an automorphism. For such a triple
$H_{3}(B)$
, and thus defines such an automorphism. For such a triple
![]() $(t,\tilde{t},\unicode[STIX]{x1D706})$
, one defines a map
$(t,\tilde{t},\unicode[STIX]{x1D706})$
, one defines a map
 $m(t):W\rightarrow W$
via
$m(t):W\rightarrow W$
via
 $$\begin{eqnarray}(a,b,c,d)m(t)=(\unicode[STIX]{x1D706}a,t(b),\tilde{t}(c),\unicode[STIX]{x1D706}^{-1}d).\end{eqnarray}$$
$$\begin{eqnarray}(a,b,c,d)m(t)=(\unicode[STIX]{x1D706}a,t(b),\tilde{t}(c),\unicode[STIX]{x1D706}^{-1}d).\end{eqnarray}$$
It is immediate that
![]() $m(t)$
defines an element of
$m(t)$
defines an element of
![]() $\text{G}$
with similitude 1.
$\text{G}$
with similitude 1.
We now define the rank of an element of
![]() $W$
. First, polarizing the quartic form
$W$
. First, polarizing the quartic form
![]() $Q$
, there is a unique symmetric 4-linear form on
$Q$
, there is a unique symmetric 4-linear form on
![]() $W$
that satisfies
$W$
that satisfies
 $(v,v,v,v)=Q(v)$
for all
$(v,v,v,v)=Q(v)$
for all
![]() $v$
in
$v$
in
![]() $W$
.
$W$
.
Definition 2.4. All elements of
![]() $W$
have rank less than or equal to four. An element
$W$
have rank less than or equal to four. An element
![]() $v$
of
$v$
of
![]() $W$
is of rank less than or equal to three if
$W$
is of rank less than or equal to three if
 $Q(v)=(v,v,v,v)=0$
. An element
$Q(v)=(v,v,v,v)=0$
. An element
![]() $v$
is of rank less than or equal to two if
$v$
is of rank less than or equal to two if
 $(v,v,v,w)=0$
for all
$(v,v,v,w)=0$
for all
![]() $w$
in
$w$
in
![]() $W$
. An element
$W$
. An element
![]() $v$
is of rank less than or equal to one if
$v$
is of rank less than or equal to one if
 $(v,v,w,w^{\prime })=0$
for all
$(v,v,w,w^{\prime })=0$
for all
![]() $w$
in
$w$
in
![]() $W$
and
$W$
and
![]() $w^{\prime }$
in
$w^{\prime }$
in
![]() $(Fv)^{\bot }$
. Here
$(Fv)^{\bot }$
. Here
![]() $(Fv)^{\bot }$
is the set of
$(Fv)^{\bot }$
is the set of
![]() $x\in W$
with
$x\in W$
with
 $\langle v,x\rangle =0$
. Finally,
$\langle v,x\rangle =0$
. Finally,
![]() $0$
is the unique element of rank zero. Since
$0$
is the unique element of rank zero. Since
![]() $\text{G}$
preserves the symplectic and the 4-linear form,
$\text{G}$
preserves the symplectic and the 4-linear form,
![]() $\text{G}$
preserves the rank of elements of
$\text{G}$
preserves the rank of elements of
![]() $W$
.
$W$
.
Elements of
![]() $W$
of rank one will play an important role in this paper. For example,
$W$
of rank one will play an important role in this paper. For example,
 $f=(0,0,0,1)$
is of rank one, and then applying
$f=(0,0,0,1)$
is of rank one, and then applying
![]() $\overline{n}(X)$
for
$\overline{n}(X)$
for
![]() $X$
in
$X$
in
![]() $H_{3}(B)$
, one gets
$H_{3}(B)$
, one gets
 $(N(X),X^{\#},X,1)$
is rank one. To check that
$(N(X),X^{\#},X,1)$
is rank one. To check that
![]() $f$
is rank one, the reader must simply observe (immediately) that the coefficient of
$f$
is rank one, the reader must simply observe (immediately) that the coefficient of
![]() $\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }$
in
$\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }$
in
 $Q(f+\unicode[STIX]{x1D707}w+\unicode[STIX]{x1D707}^{\prime }w^{\prime })$
is zero for general
$Q(f+\unicode[STIX]{x1D707}w+\unicode[STIX]{x1D707}^{\prime }w^{\prime })$
is zero for general
 $w=(a,b,c,d)$
and
$w=(a,b,c,d)$
and
 $w^{\prime }=(0,b^{\prime },c^{\prime },d^{\prime })$
in
$w^{\prime }=(0,b^{\prime },c^{\prime },d^{\prime })$
in
![]() $W$
.
$W$
.
It is easy to check that all the elements of rank one are in a single
![]() $\text{G}$
orbit. For example, one argument goes as follows. First, by applying operators
$\text{G}$
orbit. For example, one argument goes as follows. First, by applying operators
![]() $n(X)$
,
$n(X)$
,
![]() $J_{6}$
, and scalar multiplication, it is easy to see that every element
$J_{6}$
, and scalar multiplication, it is easy to see that every element
![]() $v$
of
$v$
of
![]() $W$
can be moved to one with
$W$
can be moved to one with
![]() $d=1$
. Then applying
$d=1$
. Then applying
![]() $\overline{n}(X)$
, every element has a
$\overline{n}(X)$
, every element has a
![]() $\text{G}$
translate of the form
$\text{G}$
translate of the form
 $v_{0}=(z,y,0,1)$
. Now, if
$v_{0}=(z,y,0,1)$
. Now, if
![]() $v$
and thus
$v$
and thus
![]() $v_{0}$
is rank one, then
$v_{0}$
is rank one, then
 $(v_{0},v_{0},w,w^{\prime })=0$
for arbitrary
$(v_{0},v_{0},w,w^{\prime })=0$
for arbitrary
 $w=(0,b,c,0)$
,
$w=(0,b,c,0)$
,
 $w^{\prime }=(0,b^{\prime },0,0)$
. The coefficient of
$w^{\prime }=(0,b^{\prime },0,0)$
. The coefficient of
![]() $2\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }$
in
$2\unicode[STIX]{x1D707}\unicode[STIX]{x1D707}^{\prime }$
in
 $Q(v_{0}+\unicode[STIX]{x1D707}w+\unicode[STIX]{x1D707}w^{\prime })$
is now easy to compute, and it is found to be
$Q(v_{0}+\unicode[STIX]{x1D707}w+\unicode[STIX]{x1D707}w^{\prime })$
is now easy to compute, and it is found to be
 $2\operatorname{tr}(y,b\times b^{\prime })-z\operatorname{tr}(b^{\prime },c)$
. Since this must be zero for all
$2\operatorname{tr}(y,b\times b^{\prime })-z\operatorname{tr}(b^{\prime },c)$
. Since this must be zero for all
![]() $b,b^{\prime },c$
, it follows that
$b,b^{\prime },c$
, it follows that
![]() $y$
and
$y$
and
![]() $z$
are zero, by the nondegeneracy of the two pairings. Hence
$z$
are zero, by the nondegeneracy of the two pairings. Hence
 $v_{0}=(0,0,0,1)=f$
.
$v_{0}=(0,0,0,1)=f$
.
If
![]() $v$
is a rank-one element, the stabilizer in
$v$
is a rank-one element, the stabilizer in
![]() $\text{G}$
of the line
$\text{G}$
of the line
![]() $Fv$
is a parabolic subgroup of
$Fv$
is a parabolic subgroup of
![]() $\text{G}$
. Indeed, consider the set of flags of the form
$\text{G}$
. Indeed, consider the set of flags of the form
 $0\subseteq \ell \subseteq W^{\prime }\subseteq W$
where
$0\subseteq \ell \subseteq W^{\prime }\subseteq W$
where
![]() $\ell$
is dimension one and
$\ell$
is dimension one and
![]() $W^{\prime }$
is codimension one. The conditions
$W^{\prime }$
is codimension one. The conditions
 $\langle v,w^{\prime }\rangle =0$
and
$\langle v,w^{\prime }\rangle =0$
and
 $(v,v,w,w^{\prime })=0$
for all
$(v,v,w,w^{\prime })=0$
for all
![]() $v\in \ell$
,
$v\in \ell$
,
 $w^{\prime }\in W^{\prime }$
and
$w^{\prime }\in W^{\prime }$
and
![]() $w\in W$
clearly form closed conditions on the Grassmanian of flags of these dimensions. Since these conditions single out the rank-one lines, and since
$w\in W$
clearly form closed conditions on the Grassmanian of flags of these dimensions. Since these conditions single out the rank-one lines, and since
![]() $\text{G}$
acts transitively on these lines, the stabilizer of a rank-one line is a parabolic subgroup.
$\text{G}$
acts transitively on these lines, the stabilizer of a rank-one line is a parabolic subgroup.
The argument above also shows that if
 $(z,y,x,1)$
is rank one, then
$(z,y,x,1)$
is rank one, then
![]() $y=x^{\#}$
and
$y=x^{\#}$
and
 $z=N(x)$
. (Just apply
$z=N(x)$
. (Just apply
![]() $\overline{n}(-x)$
to
$\overline{n}(-x)$
to
 $(z,y,x,1)$
.) In fact, the following is true.
$(z,y,x,1)$
.) In fact, the following is true.
Proposition 2.5. The element
 $(a,b,c,d)$
has rank at most one if and only if
$(a,b,c,d)$
has rank at most one if and only if
 $b^{\#}=ac,c^{\#}=db$
,
$b^{\#}=ac,c^{\#}=db$
,
![]() $bc=cb$
, and
$bc=cb$
, and
 $ad=bc$
. Here, the products
$ad=bc$
. Here, the products
![]() $bc$
and
$bc$
and
![]() $cb$
are taken in
$cb$
are taken in
![]() $M_{3}(B)$
.
$M_{3}(B)$
.
A proof of the proposition may be found in [Reference Gan and SavinGS05, Proposition 11.2].
3 Arithmetic invariant theory
In this section we review the arithmetic invariant theory of Gross and Lucianovic [Reference Gross and LucianovicGL09], and extend it slightly. The results in [Reference Gross and LucianovicGL09] relate ternary quadratic forms to orders in quaternion algebras, together with a nice basis of this order, up to isomorphism. The reader should consult Gross and Lucianovic [Reference Gross and LucianovicGL09] and Voight [Reference VoightVoi11] for more details and related results.
The relation between ternary quadratic forms and quaternion algebras has a long history, going back at least to Brandt [Reference BrandtBra28], Eichler [Reference EichlerEic52], and Brzezinksi [Reference BrzezińskiBrz83, Reference BrzezińskiBrz82]. It has been studied by many others as well, and from varying perspectives. The formulation of [Reference Gross and LucianovicGL09] turns out to be very well suited for our analysis of the Rankin–Selberg integral.
First, following [Reference Gross and LucianovicGL09], a quaternion ring is defined as follows. Suppose
![]() $R$
is a commutative ring, and
$R$
is a commutative ring, and
![]() $\unicode[STIX]{x1D6EC}$
is an associative
$\unicode[STIX]{x1D6EC}$
is an associative
![]() $R$
-algebra with unit. Then
$R$
-algebra with unit. Then
![]() $\unicode[STIX]{x1D6EC}$
is a quaternion ring over
$\unicode[STIX]{x1D6EC}$
is a quaternion ring over
![]() $R$
if the following properties are satisfied.
$R$
if the following properties are satisfied.
-
–
 $\unicode[STIX]{x1D6EC}$
is free of rank four as an
$\unicode[STIX]{x1D6EC}$
is free of rank four as an
 $R$
-module, and
$R$
-module, and
 $\unicode[STIX]{x1D6EC}/(R\cdot 1)$
is free of rank three.
$\unicode[STIX]{x1D6EC}/(R\cdot 1)$
is free of rank three. -
– There is an
 $R$
-linear anti-involution
$R$
-linear anti-involution
 $x\mapsto x^{\ast }$
on
$x\mapsto x^{\ast }$
on
 $\unicode[STIX]{x1D6EC}$
, such that
$\unicode[STIX]{x1D6EC}$
, such that
 $x^{\ast }=x$
for
$x^{\ast }=x$
for
 $x$
in
$x$
in
 $R$
, and
$R$
, and
 $\operatorname{tr}(x):=x+x^{\ast }$
,
$\operatorname{tr}(x):=x+x^{\ast }$
,
 $n(x):=xx^{\ast }$
are in
$n(x):=xx^{\ast }$
are in
 $R$
.
$R$
. -
– If
 $x\in \unicode[STIX]{x1D6EC}$
, then left multiplication by
$x\in \unicode[STIX]{x1D6EC}$
, then left multiplication by
 $x$
on
$x$
on
 $\unicode[STIX]{x1D6EC}$
has trace
$\unicode[STIX]{x1D6EC}$
has trace
 $2\operatorname{tr}(x)$
.
$2\operatorname{tr}(x)$
.
For instance then, if
![]() $x\in \unicode[STIX]{x1D6EC}$
, then
$x\in \unicode[STIX]{x1D6EC}$
, then
 $x^{2}=\operatorname{tr}(x)x-n(x)$
. Note that we always assume our quaternion rings are free; a vast generalization is considered in [Reference VoightVoi11]. The following definition and lemma from [Reference Gross and LucianovicGL09] are crucial.
$x^{2}=\operatorname{tr}(x)x-n(x)$
. Note that we always assume our quaternion rings are free; a vast generalization is considered in [Reference VoightVoi11]. The following definition and lemma from [Reference Gross and LucianovicGL09] are crucial.
Definition 3.1 [Reference Gross and LucianovicGL09].
Suppose
 $1,v_{1},v_{2},v_{3}$
form a basis of the quaternion ring
$1,v_{1},v_{2},v_{3}$
form a basis of the quaternion ring
![]() $\unicode[STIX]{x1D6EC}$
. Then
$\unicode[STIX]{x1D6EC}$
. Then
 $1,v_{1},v_{2},v_{3}$
are said to form a good basis if there exist
$1,v_{1},v_{2},v_{3}$
are said to form a good basis if there exist
![]() $a,b,c$
in
$a,b,c$
in
![]() $R$
such that the matrix
$R$
such that the matrix
 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}a & v_{3} & v_{2}^{\ast }\\ v_{3}^{\ast } & b & v_{1}\\ v_{2} & v_{1}^{\ast } & c\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccc@{}}a & v_{3} & v_{2}^{\ast }\\ v_{3}^{\ast } & b & v_{1}\\ v_{2} & v_{1}^{\ast } & c\end{array}\right)\end{eqnarray}$$
is rank one in the sense of Definition 2.1. Equivalently, the basis
 $1,v_{1},v_{2},v_{3}$
is a good basis if there exists
$1,v_{1},v_{2},v_{3}$
is a good basis if there exists
![]() $a,b,c$
in
$a,b,c$
in
![]() $R$
such that
$R$
such that
 $$\begin{eqnarray}v_{2}v_{3}=av_{1}^{\ast };\quad v_{3}v_{1}=bv_{2}^{\ast };\quad v_{1}v_{2}=cv_{3}^{\ast };\end{eqnarray}$$
$$\begin{eqnarray}v_{2}v_{3}=av_{1}^{\ast };\quad v_{3}v_{1}=bv_{2}^{\ast };\quad v_{1}v_{2}=cv_{3}^{\ast };\end{eqnarray}$$
and
 $$\begin{eqnarray}n(v_{1})=bc;\quad n(v_{2})=ca;\quad n(v_{3})=ab.\end{eqnarray}$$
$$\begin{eqnarray}n(v_{1})=bc;\quad n(v_{2})=ca;\quad n(v_{3})=ab.\end{eqnarray}$$
The formulas (3.2) and (3.3) are how good bases are defined in [Reference Gross and LucianovicGL09]. That one can equivalently define good bases in terms of the
![]() $A$
of (3.1) being rank one is suggested by [Reference LucianovicLuc03, Proposition 2.5.2]. Gross and Lucianovic prove the following lemma.
$A$
of (3.1) being rank one is suggested by [Reference LucianovicLuc03, Proposition 2.5.2]. Gross and Lucianovic prove the following lemma.
Lemma 3.2 [Reference Gross and LucianovicGL09].
If
 $1,w_{1},w_{2},w_{3}$
are a basis of
$1,w_{1},w_{2},w_{3}$
are a basis of
![]() $\unicode[STIX]{x1D6EC}$
, then there exist unique
$\unicode[STIX]{x1D6EC}$
, then there exist unique
 $x_{1},x_{2},x_{3}$
in
$x_{1},x_{2},x_{3}$
in
![]() $R$
so that
$R$
so that
 $v_{i}:=w_{i}-x_{i}$
form a good basis.
$v_{i}:=w_{i}-x_{i}$
form a good basis.
Let us very briefly sketch a proof. Consider the structure coefficients of
![]() $\unicode[STIX]{x1D6EC}$
, namely, those elements
$\unicode[STIX]{x1D6EC}$
, namely, those elements
![]() $s_{ij}^{k}$
in
$s_{ij}^{k}$
in
![]() $R$
so that
$R$
so that
 $$\begin{eqnarray}w_{i}w_{j}=s_{ij}^{0}+s_{ij}^{1}w_{1}+s_{ij}^{2}w_{2}+s_{ij}^{3}w_{3}.\end{eqnarray}$$
$$\begin{eqnarray}w_{i}w_{j}=s_{ij}^{0}+s_{ij}^{1}w_{1}+s_{ij}^{2}w_{2}+s_{ij}^{3}w_{3}.\end{eqnarray}$$
The key point is that the definition of the quaternion ring forces the matrix
 $$\begin{eqnarray}S:=\left(\begin{array}{@{}ccc@{}}s_{23}^{1} & s_{23}^{2} & s_{23}^{3}\\ s_{31}^{1} & s_{31}^{2} & s_{31}^{3}\\ s_{12}^{1} & s_{12}^{2} & s_{12}^{3}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}S:=\left(\begin{array}{@{}ccc@{}}s_{23}^{1} & s_{23}^{2} & s_{23}^{3}\\ s_{31}^{1} & s_{31}^{2} & s_{31}^{3}\\ s_{12}^{1} & s_{12}^{2} & s_{12}^{3}\end{array}\right)\end{eqnarray}$$
to be symmetric. For example, to see that
 $s_{23}^{2}=s_{31}^{1}$
, one considers the trace of left multiplication by
$s_{23}^{2}=s_{31}^{1}$
, one considers the trace of left multiplication by
![]() $w_{3}$
on
$w_{3}$
on
![]() $\unicode[STIX]{x1D6EC}$
. Using the expression for
$\unicode[STIX]{x1D6EC}$
. Using the expression for
![]() $w_{2}w_{3}$
in terms of the structure constants, and conjugating it, one can obtain that the trace is
$w_{2}w_{3}$
in terms of the structure constants, and conjugating it, one can obtain that the trace is
 $2\operatorname{tr}(w_{3})+s_{31}^{1}-s_{23}^{2}$
. Consequently,
$2\operatorname{tr}(w_{3})+s_{31}^{1}-s_{23}^{2}$
. Consequently,
 $s_{31}^{1}=s_{23}^{2}$
. One sets
$s_{31}^{1}=s_{23}^{2}$
. One sets
 $x_{1}=s_{31}^{3}=s_{12}^{2}$
,
$x_{1}=s_{31}^{3}=s_{12}^{2}$
,
 $x_{2}=s_{12}^{1}=s_{23}^{3}$
, and
$x_{2}=s_{12}^{1}=s_{23}^{3}$
, and
 $x_{3}=s_{23}^{2}=s_{31}^{1}$
. Then
$x_{3}=s_{23}^{2}=s_{31}^{1}$
. Then
 $v_{i}=w_{i}-x_{i}$
is the good basis. In fact, if
$v_{i}=w_{i}-x_{i}$
is the good basis. In fact, if
 $$\begin{eqnarray}W=\left(\begin{array}{@{}ccc@{}} & w_{3} & w_{2}^{\ast }\\ w_{3}^{\ast } & & w_{1}\\ w_{2} & w_{1}^{\ast } & \end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}W=\left(\begin{array}{@{}ccc@{}} & w_{3} & w_{2}^{\ast }\\ w_{3}^{\ast } & & w_{1}\\ w_{2} & w_{1}^{\ast } & \end{array}\right),\end{eqnarray}$$
then using the associativity of the multiplication in
![]() $\unicode[STIX]{x1D6EC}$
and that
$\unicode[STIX]{x1D6EC}$
and that
 $1,v_{1},v_{2},v_{3}$
is a basis, one can check that
$1,v_{1},v_{2},v_{3}$
is a basis, one can check that
![]() $W-S$
is rank one. The uniqueness of the
$W-S$
is rank one. The uniqueness of the
![]() $x_{i}$
is immediate. For a slightly different proof, but more details, consult [Reference Gross and LucianovicGL09].
$x_{i}$
is immediate. For a slightly different proof, but more details, consult [Reference Gross and LucianovicGL09].
Suppose now that
 $v_{1},v_{2},v_{3}$
is a good basis, and
$v_{1},v_{2},v_{3}$
is a good basis, and
![]() $A$
is the rank-one matrix in (3.1). Associated to
$A$
is the rank-one matrix in (3.1). Associated to
![]() $A$
, one can form the ternary quadratic form
$A$
, one can form the ternary quadratic form
 $$\begin{eqnarray}q_{T}(x,y,z)=ax^{2}+by^{2}+cz^{2}+dyz+ezx+fxy,\end{eqnarray}$$
$$\begin{eqnarray}q_{T}(x,y,z)=ax^{2}+by^{2}+cz^{2}+dyz+ezx+fxy,\end{eqnarray}$$
where
 $d=\operatorname{tr}(v_{1})$
,
$d=\operatorname{tr}(v_{1})$
,
 $e=\operatorname{tr}(v_{2})$
,
$e=\operatorname{tr}(v_{2})$
,
 $f=\operatorname{tr}(v_{3})$
. Equivalently, if
$f=\operatorname{tr}(v_{3})$
. Equivalently, if
![]() $2$
is not a zero-divisor in
$2$
is not a zero-divisor in
![]() $R$
, one can form the half-integral symmetric matrix
$R$
, one can form the half-integral symmetric matrix
 $$\begin{eqnarray}T=\left(\begin{array}{@{}ccc@{}}a & {\displaystyle \frac{f}{2}} & {\displaystyle \frac{e}{2}}\\ {\displaystyle \frac{f}{2}} & b & {\displaystyle \frac{d}{2}}\\ {\displaystyle \frac{e}{2}} & {\displaystyle \frac{d}{2}} & c\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}T=\left(\begin{array}{@{}ccc@{}}a & {\displaystyle \frac{f}{2}} & {\displaystyle \frac{e}{2}}\\ {\displaystyle \frac{f}{2}} & b & {\displaystyle \frac{d}{2}}\\ {\displaystyle \frac{e}{2}} & {\displaystyle \frac{d}{2}} & c\end{array}\right).\end{eqnarray}$$
The strength of the definition of good basis is that
![]() $q_{T}$
determines all the multiplication rules in the quaternion ring. For instance,
$q_{T}$
determines all the multiplication rules in the quaternion ring. For instance,
 $v_{1}^{2}=dv_{1}-bc$
,
$v_{1}^{2}=dv_{1}-bc$
,
 $v_{1}v_{2}=cv_{3}^{\ast }=cf-cv_{3}$
, and
$v_{1}v_{2}=cv_{3}^{\ast }=cf-cv_{3}$
, and
 $$\begin{eqnarray}v_{2}v_{1}=(e-v_{2})(d-v_{1})-de+ev_{1}+dv_{2}=-de+ev_{1}+dv_{2}+cv_{3}.\end{eqnarray}$$
$$\begin{eqnarray}v_{2}v_{1}=(e-v_{2})(d-v_{1})-de+ev_{1}+dv_{2}=-de+ev_{1}+dv_{2}+cv_{3}.\end{eqnarray}$$
Conversely, starting with a ternary quadratic form
 $q_{T}(x,y,z)=ax^{2}+by^{2}+cz^{2}+dyz+ezx+fxy$
on
$q_{T}(x,y,z)=ax^{2}+by^{2}+cz^{2}+dyz+ezx+fxy$
on
![]() $R^{3}$
, there is the data of a quaternion ring
$R^{3}$
, there is the data of a quaternion ring
![]() $\unicode[STIX]{x1D6EC}_{T}$
over
$\unicode[STIX]{x1D6EC}_{T}$
over
![]() $R$
, together with a good basis of
$R$
, together with a good basis of
![]() $\unicode[STIX]{x1D6EC}_{T}$
, as follows. Let us write
$\unicode[STIX]{x1D6EC}_{T}$
, as follows. Let us write
 $N=R^{3}$
, with basis
$N=R^{3}$
, with basis
 $e_{1}=(1,0,0)$
,
$e_{1}=(1,0,0)$
,
 $e_{2}=(0,1,0),e_{3}=(0,0,1)$
. One puts on
$e_{2}=(0,1,0),e_{3}=(0,0,1)$
. One puts on
![]() $N$
the quadratic form
$N$
the quadratic form
 $$\begin{eqnarray}q_{T}(xe_{1}+ye_{2}+ze_{3})=ax^{2}+by^{2}+cz^{2}+dyz+ezx+fxy.\end{eqnarray}$$
$$\begin{eqnarray}q_{T}(xe_{1}+ye_{2}+ze_{3})=ax^{2}+by^{2}+cz^{2}+dyz+ezx+fxy.\end{eqnarray}$$
Then, one can construct the even Clifford algebra
 $C^{+}((N,q_{T}))$
, defined as usual to be the even-degree part of the tensor algebra of
$C^{+}((N,q_{T}))$
, defined as usual to be the even-degree part of the tensor algebra of
![]() $N$
, modulo the ideal generated by the relations
$N$
, modulo the ideal generated by the relations
 $v^{2}=q_{T}(v)$
for
$v^{2}=q_{T}(v)$
for
![]() $v\in N$
.
$v\in N$
.
 $C^{+}((N,q_{T}))$
is a free
$C^{+}((N,q_{T}))$
is a free
![]() $R$
-module of rank four; it is the quaternion ring
$R$
-module of rank four; it is the quaternion ring
![]() $\unicode[STIX]{x1D6EC}_{T}$
. The map
$\unicode[STIX]{x1D6EC}_{T}$
. The map
 $v_{1}v_{2}\cdots v_{r}\mapsto v_{r}\cdots v_{2}v_{1}$
on the tensor algebra descends to an involution on
$v_{1}v_{2}\cdots v_{r}\mapsto v_{r}\cdots v_{2}v_{1}$
on the tensor algebra descends to an involution on
![]() $\unicode[STIX]{x1D6EC}_{T}$
. This involution is the conjugation
$\unicode[STIX]{x1D6EC}_{T}$
. This involution is the conjugation
![]() $v\mapsto v^{\ast }$
on the quaternion algebra. The preferred choice of basis of
$v\mapsto v^{\ast }$
on the quaternion algebra. The preferred choice of basis of
![]() $\unicode[STIX]{x1D6EC}_{T}$
is the element 1, together with
$\unicode[STIX]{x1D6EC}_{T}$
is the element 1, together with
 $v_{1}=e_{2}e_{3},v_{2}=e_{3}e_{1},v_{3}=e_{1}e_{2}$
. It is immediate that this is a good basis, because it is essentially the definition of the Clifford algebra
$v_{1}=e_{2}e_{3},v_{2}=e_{3}e_{1},v_{3}=e_{1}e_{2}$
. It is immediate that this is a good basis, because it is essentially the definition of the Clifford algebra
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}e_{1}\\ e_{2}\\ e_{3}\end{array}\right)\left(\begin{array}{@{}ccc@{}}e_{1} & e_{2} & e_{3}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}a & v_{3} & v_{2}^{\ast }\\ v_{3}^{\ast } & b & v_{1}\\ v_{2} & v_{1}^{\ast } & c\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}e_{1}\\ e_{2}\\ e_{3}\end{array}\right)\left(\begin{array}{@{}ccc@{}}e_{1} & e_{2} & e_{3}\end{array}\right)=\left(\begin{array}{@{}ccc@{}}a & v_{3} & v_{2}^{\ast }\\ v_{3}^{\ast } & b & v_{1}\\ v_{2} & v_{1}^{\ast } & c\end{array}\right)\end{eqnarray}$$
that the matrix on the right factorizes as on the left, and thus (heuristically, at least) is rank one.
If
 $\unicode[STIX]{x1D6EC},(v_{1},v_{2},v_{3})$
,
$\unicode[STIX]{x1D6EC},(v_{1},v_{2},v_{3})$
,
 $\unicode[STIX]{x1D6EC}^{\prime },(v_{1}^{\prime },v_{2}^{\prime },v_{3}^{\prime })$
are two quaternion rings over
$\unicode[STIX]{x1D6EC}^{\prime },(v_{1}^{\prime },v_{2}^{\prime },v_{3}^{\prime })$
are two quaternion rings over
![]() $R$
with good bases, we say a map
$R$
with good bases, we say a map
 $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}^{\prime }$
is an isomorphism of good-based quaternion rings if
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D6EC}\rightarrow \unicode[STIX]{x1D6EC}^{\prime }$
is an isomorphism of good-based quaternion rings if
![]() $\unicode[STIX]{x1D719}$
is an isomorphism of
$\unicode[STIX]{x1D719}$
is an isomorphism of
![]() $R$
-algebras, preserving the involution, and
$R$
-algebras, preserving the involution, and
 $\unicode[STIX]{x1D719}(v_{i})=v_{i}^{\prime }$
,
$\unicode[STIX]{x1D719}(v_{i})=v_{i}^{\prime }$
,
 $i=1,2,3$
. The constructions associating a ternary quadratic form
$i=1,2,3$
. The constructions associating a ternary quadratic form
![]() $q_{T}$
to a good-based quaternion ring and the even Clifford algebra to a ternary quadratic form are inverse to one another. Furthermore, there is a notion of ‘reduced discriminant’ of quaternion rings, see [Reference Gross and LucianovicGL09, p. 8], and similarly for ternary quadratic forms.
$q_{T}$
to a good-based quaternion ring and the even Clifford algebra to a ternary quadratic form are inverse to one another. Furthermore, there is a notion of ‘reduced discriminant’ of quaternion rings, see [Reference Gross and LucianovicGL09, p. 8], and similarly for ternary quadratic forms.
Proposition 3.3 (Gross and Lucianovic [Reference Gross and LucianovicGL09]).
Every quaternion ring has a good basis. The even Clifford construction induces a discriminant preserving bijection between ternary quadratic forms
![]() $q_{T}$
and isomorphism classes of good-based quaternion rings.
$q_{T}$
and isomorphism classes of good-based quaternion rings.
They furthermore give a
 $\operatorname{GL}_{3}(R)$
action on ternary quadratic forms, and on good bases, and then descend the bijection in the proposition to a bijection between
$\operatorname{GL}_{3}(R)$
action on ternary quadratic forms, and on good bases, and then descend the bijection in the proposition to a bijection between
 $\operatorname{GL}_{3}(R)$
orbits of ternary quadratic forms and isomorphism classes of quaternion rings over
$\operatorname{GL}_{3}(R)$
orbits of ternary quadratic forms and isomorphism classes of quaternion rings over
![]() $R$
.
$R$
.
Because the bijection of Proposition 3.3 preserves discriminant, one obtains the following corollary.
Corollary 3.4. Suppose the half-integral symmetric matrix
![]() $T$
corresponds to a maximal order in a quaternion algebra
$T$
corresponds to a maximal order in a quaternion algebra
![]() $B$
over
$B$
over
![]() $\mathbf{Q}$
. Denote by
$\mathbf{Q}$
. Denote by
 $D_{B}=\prod _{p\;\text{ram}}p$
the product of the primes
$D_{B}=\prod _{p\;\text{ram}}p$
the product of the primes
![]() $p$
for which
$p$
for which
 $B\otimes \mathbf{Q}_{p}$
is nonsplit. Then
$B\otimes \mathbf{Q}_{p}$
is nonsplit. Then
 $4\det (T)=\pm D_{B}$
.
$4\det (T)=\pm D_{B}$
.
We now work over
![]() $\mathbf{Z}$
. If
$\mathbf{Z}$
. If
![]() $\unicode[STIX]{x1D6EC}$
is a quaternion ring, and
$\unicode[STIX]{x1D6EC}$
is a quaternion ring, and
![]() $x\in \unicode[STIX]{x1D6EC}$
, we denote by
$x\in \unicode[STIX]{x1D6EC}$
, we denote by
![]() $\operatorname{Im}(x)$
the element of
$\operatorname{Im}(x)$
the element of
![]() $\unicode[STIX]{x1D6EC}\otimes \mathbf{Q}$
with
$\unicode[STIX]{x1D6EC}\otimes \mathbf{Q}$
with
 $x=\operatorname{tr}(x)/2+\operatorname{Im}(x)$
. The following lemma is the same as the uniqueness of the
$x=\operatorname{tr}(x)/2+\operatorname{Im}(x)$
. The following lemma is the same as the uniqueness of the
![]() $x_{i}$
so that
$x_{i}$
so that
![]() $w_{i}-x_{i}$
form a good basis.
$w_{i}-x_{i}$
form a good basis.
Lemma 3.5. Suppose
![]() $B$
a quaternion algebra over
$B$
a quaternion algebra over
![]() $\mathbf{Q}$
,
$\mathbf{Q}$
,
 $A_{1},A_{2}\in H_{3}(B)$
. Suppose furthermore that the off-diagonal elements of
$A_{1},A_{2}\in H_{3}(B)$
. Suppose furthermore that the off-diagonal elements of
![]() $A_{1}$
span the three-dimensional
$A_{1}$
span the three-dimensional
![]() $\mathbf{Q}$
vector space
$\mathbf{Q}$
vector space
 $B/(\mathbf{Q}\cdot 1)$
, and similarly for
$B/(\mathbf{Q}\cdot 1)$
, and similarly for
![]() $A_{2}$
. If
$A_{2}$
. If
![]() $A_{1},A_{2}$
are rank-one matrices with
$A_{1},A_{2}$
are rank-one matrices with
 $\operatorname{Im}(A_{1})=\operatorname{Im}(A_{2})$
, then
$\operatorname{Im}(A_{1})=\operatorname{Im}(A_{2})$
, then
 $A_{1}=A_{2}$
.
$A_{1}=A_{2}$
.
Below we will require the following definition.
Definition 3.6. Suppose
![]() $T$
is a half-integral symmetric matrix, with entries as in (3.4). Let
$T$
is a half-integral symmetric matrix, with entries as in (3.4). Let
 $\unicode[STIX]{x1D6EC}_{T},(v_{1},v_{2},v_{3})$
be the associated quaternion ring with good basis. We define
$\unicode[STIX]{x1D6EC}_{T},(v_{1},v_{2},v_{3})$
be the associated quaternion ring with good basis. We define
![]() $A(T)$
to be the matrix
$A(T)$
to be the matrix
 $$\begin{eqnarray}A(T)=\left(\begin{array}{@{}ccc@{}}a & v_{3} & v_{2}^{\ast }\\ v_{3}^{\ast } & b & v_{1}\\ v_{2} & v_{1}^{\ast } & c\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}A(T)=\left(\begin{array}{@{}ccc@{}}a & v_{3} & v_{2}^{\ast }\\ v_{3}^{\ast } & b & v_{1}\\ v_{2} & v_{1}^{\ast } & c\end{array}\right).\end{eqnarray}$$
One has that
![]() $A(T)$
is rank one in the sense of Definition 2.1.
$A(T)$
is rank one in the sense of Definition 2.1.
For further applications, one wants to understand suborders of quaternion orders, together with their good bases. Let
![]() $T$
be a half-integral symmetric matrix, and
$T$
be a half-integral symmetric matrix, and
 $\unicode[STIX]{x1D6EC}_{T},(v_{1},v_{2},v_{3})$
the associated quaternion ring with its good basis. Suppose
$\unicode[STIX]{x1D6EC}_{T},(v_{1},v_{2},v_{3})$
the associated quaternion ring with its good basis. Suppose
 $m\in M_{3}(\mathbf{Z})\cap \operatorname{GL}_{3}(\mathbf{Q})$
. Consider the three elements
$m\in M_{3}(\mathbf{Z})\cap \operatorname{GL}_{3}(\mathbf{Q})$
. Consider the three elements
 $w_{1},w_{2},w_{3}\in \unicode[STIX]{x1D6EC}_{T}$
defined by the matrix equation
$w_{1},w_{2},w_{3}\in \unicode[STIX]{x1D6EC}_{T}$
defined by the matrix equation
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}w_{1} & w_{2} & w_{3}\end{array}\right):=\left(\begin{array}{@{}ccc@{}}v_{1} & v_{2} & v_{3}\end{array}\right)m.\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}w_{1} & w_{2} & w_{3}\end{array}\right):=\left(\begin{array}{@{}ccc@{}}v_{1} & v_{2} & v_{3}\end{array}\right)m.\end{eqnarray}$$
That is,
 $w_{i}=\sum _{j}m_{ji}v_{j}$
. Now consider the lattice
$w_{i}=\sum _{j}m_{ji}v_{j}$
. Now consider the lattice
 $\unicode[STIX]{x1D6EC}_{T}(m)\subset \unicode[STIX]{x1D6EC}_{T}$
spanned by
$\unicode[STIX]{x1D6EC}_{T}(m)\subset \unicode[STIX]{x1D6EC}_{T}$
spanned by
 $1,w_{1},w_{2},w_{3}$
. It is a natural question to ask when the lattice
$1,w_{1},w_{2},w_{3}$
. It is a natural question to ask when the lattice
![]() $\unicode[STIX]{x1D6EC}_{T}(m)$
is closed under multiplication. Lemma 3.8 below answers this question.
$\unicode[STIX]{x1D6EC}_{T}(m)$
is closed under multiplication. Lemma 3.8 below answers this question.
Definition 3.7. For
 $m\in \operatorname{GL}_{3}$
, denote
$m\in \operatorname{GL}_{3}$
, denote
 $c(m)=\det (m)\text{}^{t}m^{-1}$
the cofactor matrix of
$c(m)=\det (m)\text{}^{t}m^{-1}$
the cofactor matrix of
![]() $m$
.
$m$
.
Lemma 3.8. Denote by
![]() $J_{T}$
the set of
$J_{T}$
the set of
![]() $3\times 3$
Hermitian matrices
$3\times 3$
Hermitian matrices
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}c_{1} & x_{3} & x_{2}^{\ast }\\ x_{3}^{\ast } & c_{2} & x_{1}\\ x_{2} & x_{1}^{\ast } & c_{3}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}c_{1} & x_{3} & x_{2}^{\ast }\\ x_{3}^{\ast } & c_{2} & x_{1}\\ x_{2} & x_{1}^{\ast } & c_{3}\end{array}\right)\end{eqnarray}$$
with
![]() $c_{i}\in \mathbf{Z}$
and
$c_{i}\in \mathbf{Z}$
and
 $x_{i}\in \unicode[STIX]{x1D6EC}_{T}$
. For
$x_{i}\in \unicode[STIX]{x1D6EC}_{T}$
. For
 $m\in \operatorname{GL}_{3}(\mathbf{Q})$
, denote by
$m\in \operatorname{GL}_{3}(\mathbf{Q})$
, denote by
![]() $v_{i}^{\prime }$
the off-diagonal entries of
$v_{i}^{\prime }$
the off-diagonal entries of
 $m^{-1}A(T)c(m)$
, and
$m^{-1}A(T)c(m)$
, and
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
the lattice in
$\unicode[STIX]{x1D6EC}^{\prime }$
the lattice in
![]() $\unicode[STIX]{x1D6EC}\otimes \mathbf{Q}$
spanned by
$\unicode[STIX]{x1D6EC}\otimes \mathbf{Q}$
spanned by
![]() $1$
and
$1$
and
 $v_{1}^{\prime },v_{2}^{\prime },v_{3}^{\prime }$
. Consider the following four statements:
$v_{1}^{\prime },v_{2}^{\prime },v_{3}^{\prime }$
. Consider the following four statements:
-
(i)
 $\unicode[STIX]{x1D6EC}_{T}(m)$
is closed under multiplication;
$\unicode[STIX]{x1D6EC}_{T}(m)$
is closed under multiplication; -
(ii)
 $m^{-1}Tc(m)$
is half-integral;
$m^{-1}Tc(m)$
is half-integral; -
(iii)
 $m^{-1}A(T)c(m)=:A^{\prime }$
is in
$m^{-1}A(T)c(m)=:A^{\prime }$
is in
 $J_{T}$
;
$J_{T}$
; -
(iv)
 $\unicode[STIX]{x1D6EC}^{\prime }$
is closed under multiplication.
$\unicode[STIX]{x1D6EC}^{\prime }$
is closed under multiplication.
Then, if
 $m\in M_{3}(\mathbf{Z})$
, all four statements are equivalent. If statement (iii) holds, then
$m\in M_{3}(\mathbf{Z})$
, all four statements are equivalent. If statement (iii) holds, then
 $m\in M_{3}(\mathbf{Z})$
. In the case these equivalent conditions are satisfied,
$m\in M_{3}(\mathbf{Z})$
. In the case these equivalent conditions are satisfied,
 $1,v_{1}^{\prime },v_{2}^{\prime },v_{3}^{\prime }$
is a good basis of
$1,v_{1}^{\prime },v_{2}^{\prime },v_{3}^{\prime }$
is a good basis of
![]() $\unicode[STIX]{x1D6EC}_{T}(m)$
.
$\unicode[STIX]{x1D6EC}_{T}(m)$
.
Actually, we prove the following stronger statement: statement (iii) implies statement (ii); statements (ii) and (iv) are equivalent. Suppose statement (i) holds, and denote by
![]() $A_{0}$
the rank-one matrix associated to the good basis of
$A_{0}$
the rank-one matrix associated to the good basis of
![]() $\unicode[STIX]{x1D6EC}_{T}(m)$
obtained by translating the
$\unicode[STIX]{x1D6EC}_{T}(m)$
obtained by translating the
![]() $w_{i}$
by integers. Then
$w_{i}$
by integers. Then
 $A_{0}=A^{\prime }$
, and thus
$A_{0}=A^{\prime }$
, and thus
 $\unicode[STIX]{x1D6EC}_{T}(m)=\unicode[STIX]{x1D6EC}^{\prime }$
. Hence statement (i) implies statement (ii), equivalently statement (iv), and if
$\unicode[STIX]{x1D6EC}_{T}(m)=\unicode[STIX]{x1D6EC}^{\prime }$
. Hence statement (i) implies statement (ii), equivalently statement (iv), and if
 $m\in M_{3}(\mathbf{Z})$
, then statement (i) implies statement (iii). If
$m\in M_{3}(\mathbf{Z})$
, then statement (i) implies statement (iii). If
 $m\in M_{3}(\mathbf{Z})$
, then statement (iv) implies
$m\in M_{3}(\mathbf{Z})$
, then statement (iv) implies
 $\unicode[STIX]{x1D6EC}_{T}(m)=\unicode[STIX]{x1D6EC}^{\prime }$
, and thus statement (iv) implies statement (i).
$\unicode[STIX]{x1D6EC}_{T}(m)=\unicode[STIX]{x1D6EC}^{\prime }$
, and thus statement (iv) implies statement (i).
Proof of Lemma 3.8.
Denote by
![]() $V_{3}$
the defining three-dimensional representation of
$V_{3}$
the defining three-dimensional representation of
![]() $\operatorname{GL}_{3}$
. One has the equivalence
$\operatorname{GL}_{3}$
. One has the equivalence
 $\wedge ^{2}V_{3}^{\ast }\otimes \det \simeq V_{3}$
. Suppose
$\wedge ^{2}V_{3}^{\ast }\otimes \det \simeq V_{3}$
. Suppose
 $x_{1},x_{2},x_{3}$
are indeterminates. In coordinates, this equivalence of representations of
$x_{1},x_{2},x_{3}$
are indeterminates. In coordinates, this equivalence of representations of
![]() $\operatorname{GL}_{3}$
amounts to the identity
$\operatorname{GL}_{3}$
amounts to the identity
 $$\begin{eqnarray}\det (m)m^{-1}\left(\begin{array}{@{}ccc@{}} & x_{3} & -x_{2}\\ -x_{3} & & x_{1}\\ x_{2} & -x_{1} & \end{array}\right)\text{}^{t}m^{-1}=\left(\begin{array}{@{}ccc@{}} & x_{3}^{\prime } & -x_{2}^{\prime }\\ -x_{3}^{\prime } & & x_{1}^{\prime }\\ x_{2}^{\prime } & -x_{1}^{\prime } & \end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\det (m)m^{-1}\left(\begin{array}{@{}ccc@{}} & x_{3} & -x_{2}\\ -x_{3} & & x_{1}\\ x_{2} & -x_{1} & \end{array}\right)\text{}^{t}m^{-1}=\left(\begin{array}{@{}ccc@{}} & x_{3}^{\prime } & -x_{2}^{\prime }\\ -x_{3}^{\prime } & & x_{1}^{\prime }\\ x_{2}^{\prime } & -x_{1}^{\prime } & \end{array}\right),\end{eqnarray}$$
where
 $x_{i}^{\prime }=\sum _{j}m_{ji}x_{j}$
. Thus since
$x_{i}^{\prime }=\sum _{j}m_{ji}x_{j}$
. Thus since
 $\operatorname{Im}(A(T))$
is antisymmetric,
$\operatorname{Im}(A(T))$
is antisymmetric,
 $$\begin{eqnarray}\operatorname{Im}(A^{\prime })=m^{-1}\operatorname{Im}(A(T))c(m)=\left(\begin{array}{@{}ccc@{}}0 & \operatorname{Im}(w_{3}) & -\operatorname{Im}(w_{2})\\ -\operatorname{Im}(w_{3}) & 0 & \operatorname{Im}(w_{1})\\ \operatorname{Im}(w_{2}) & -\operatorname{Im}(w_{1}) & 0\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Im}(A^{\prime })=m^{-1}\operatorname{Im}(A(T))c(m)=\left(\begin{array}{@{}ccc@{}}0 & \operatorname{Im}(w_{3}) & -\operatorname{Im}(w_{2})\\ -\operatorname{Im}(w_{3}) & 0 & \operatorname{Im}(w_{1})\\ \operatorname{Im}(w_{2}) & -\operatorname{Im}(w_{1}) & 0\end{array}\right).\end{eqnarray}$$
Now, immediately statement (iii) implies statement (ii), and statements (ii) and (iv) are equivalent because
 $m^{-1}Tc(m)$
exactly describes the multiplication rules for
$m^{-1}Tc(m)$
exactly describes the multiplication rules for
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
in
$\unicode[STIX]{x1D6EC}^{\prime }$
in
![]() $\unicode[STIX]{x1D6EC}\otimes \mathbf{Q}$
. Suppose now that statement (i) holds. Then one may change
$\unicode[STIX]{x1D6EC}\otimes \mathbf{Q}$
. Suppose now that statement (i) holds. Then one may change
 $w_{1},w_{2},w_{3}$
by integers to make them into a good basis. Hence we have
$w_{1},w_{2},w_{3}$
by integers to make them into a good basis. Hence we have
![]() $A_{0},A^{\prime }$
both rank one, and with the same imaginary parts by (3.7). Thus by Lemma 3.5,
$A_{0},A^{\prime }$
both rank one, and with the same imaginary parts by (3.7). Thus by Lemma 3.5,
 $A_{0}=A^{\prime }$
. Since by definition the off-diagonal entries of
$A_{0}=A^{\prime }$
. Since by definition the off-diagonal entries of
![]() $A_{0}$
generate
$A_{0}$
generate
![]() $\unicode[STIX]{x1D6EC}_{T}(m)$
, and the off-diagonal entries of
$\unicode[STIX]{x1D6EC}_{T}(m)$
, and the off-diagonal entries of
![]() $A^{\prime }$
generate
$A^{\prime }$
generate
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
, we get
$\unicode[STIX]{x1D6EC}^{\prime }$
, we get
 $\unicode[STIX]{x1D6EC}_{T}(m)=\unicode[STIX]{x1D6EC}^{\prime }$
. Hence statement (i) implies statement (iv) or equivalently statement (ii). If
$\unicode[STIX]{x1D6EC}_{T}(m)=\unicode[STIX]{x1D6EC}^{\prime }$
. Hence statement (i) implies statement (iv) or equivalently statement (ii). If
 $m\in M_{3}(\mathbf{Z})$
, then this
$m\in M_{3}(\mathbf{Z})$
, then this
![]() $A_{0}$
is in
$A_{0}$
is in
![]() $J_{T}$
, and hence when
$J_{T}$
, and hence when
![]() $m$
is integral, statement (i) implies statement (iii).
$m$
is integral, statement (i) implies statement (iii).
Now suppose statement (iv) holds, and
![]() $m$
is integral. We have that
$m$
is integral. We have that
 $\operatorname{Im}(w_{i})=\operatorname{Im}(v_{i}^{\prime })$
. Since we assume statement (iv), the
$\operatorname{Im}(w_{i})=\operatorname{Im}(v_{i}^{\prime })$
. Since we assume statement (iv), the
![]() $v_{i}^{\prime }$
have integral trace, and since
$v_{i}^{\prime }$
have integral trace, and since
![]() $m$
is integral, the
$m$
is integral, the
![]() $w_{i}$
have integral trace. Hence
$w_{i}$
have integral trace. Hence
 $w_{i}-v_{i}^{\prime }\in \frac{1}{2}\mathbf{Z}$
. We claim the difference is in
$w_{i}-v_{i}^{\prime }\in \frac{1}{2}\mathbf{Z}$
. We claim the difference is in
![]() $\mathbf{Z}$
. Indeed, write
$\mathbf{Z}$
. Indeed, write
 $v_{i}^{\prime }=w_{i}+\ell /2$
, with
$v_{i}^{\prime }=w_{i}+\ell /2$
, with
![]() $\ell$
an integer. Then
$\ell$
an integer. Then
 $$\begin{eqnarray}2N(v_{i}^{\prime })=2(w_{i}+\ell /2)(w_{i}^{\ast }+\ell /2)=2N(w_{i})+\ell \operatorname{tr}(w_{i})+\ell ^{2}/2.\end{eqnarray}$$
$$\begin{eqnarray}2N(v_{i}^{\prime })=2(w_{i}+\ell /2)(w_{i}^{\ast }+\ell /2)=2N(w_{i})+\ell \operatorname{tr}(w_{i})+\ell ^{2}/2.\end{eqnarray}$$
Again since
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
is closed under multiplication and
$\unicode[STIX]{x1D6EC}^{\prime }$
is closed under multiplication and
![]() $m$
is integral,
$m$
is integral,
![]() $v_{i}^{\prime }$
and
$v_{i}^{\prime }$
and
![]() $w_{i}$
have integral norm. Hence
$w_{i}$
have integral norm. Hence
![]() $\ell ^{2}/2$
is an integer, and thus
$\ell ^{2}/2$
is an integer, and thus
![]() $\ell$
is even. Consequently, if
$\ell$
is even. Consequently, if
![]() $m$
is integral, then statement (iv) implies
$m$
is integral, then statement (iv) implies
 $\unicode[STIX]{x1D6EC}^{\prime }=\unicode[STIX]{x1D6EC}_{T}(m)$
, and hence statement (iv) implies statement (i).
$\unicode[STIX]{x1D6EC}^{\prime }=\unicode[STIX]{x1D6EC}_{T}(m)$
, and hence statement (iv) implies statement (i).
Finally, suppose statement (iii) holds. Then by definition,
![]() $v_{i}^{\prime }$
is in
$v_{i}^{\prime }$
is in
![]() $\unicode[STIX]{x1D6EC}_{T}$
. On the other hand, we have
$\unicode[STIX]{x1D6EC}_{T}$
. On the other hand, we have
 $\operatorname{Im}(v_{i}^{\prime })=\sum _{j}m_{ji}\operatorname{Im}(v_{j})$
, and thus
$\operatorname{Im}(v_{i}^{\prime })=\sum _{j}m_{ji}\operatorname{Im}(v_{j})$
, and thus
 $v_{i}^{\prime }=a_{i}+\sum _{j}m_{ji}v_{j}$
for some
$v_{i}^{\prime }=a_{i}+\sum _{j}m_{ji}v_{j}$
for some
![]() $a_{i}$
in
$a_{i}$
in
![]() $\mathbf{Q}$
. Since
$\mathbf{Q}$
. Since
![]() $v_{i}^{\prime }$
is in
$v_{i}^{\prime }$
is in
![]() $\unicode[STIX]{x1D6EC}_{T}$
and
$\unicode[STIX]{x1D6EC}_{T}$
and
 $1,v_{1},v_{2},v_{3}$
are a basis on
$1,v_{1},v_{2},v_{3}$
are a basis on
![]() $\unicode[STIX]{x1D6EC}_{T}$
, it follows that the
$\unicode[STIX]{x1D6EC}_{T}$
, it follows that the
![]() $a_{i}$
and
$a_{i}$
and
![]() $m_{ji}$
are in
$m_{ji}$
are in
![]() $\mathbf{Z}$
, and thus
$\mathbf{Z}$
, and thus
 $m\in M_{3}(\mathbf{Z})$
, as desired.◻
$m\in M_{3}(\mathbf{Z})$
, as desired.◻
Remark 3.9. The equivalence of statements (i), (ii) and (iv) in Lemma 3.8 can also be deduced easily from [Reference VoightVoi, Proposition 22.4.12]. We thank John Voight for pointing this out to the author.
Remark 3.10. Lemma 3.8 suggests the following partial order on nondegenerate ternary quadratic forms. Suppose
 $q_{1}(x,y,z)$
and
$q_{1}(x,y,z)$
and
 $q_{2}(x,y,z)$
are integral ternary quadratic forms, with associated half-integral symmetric matrices
$q_{2}(x,y,z)$
are integral ternary quadratic forms, with associated half-integral symmetric matrices
![]() $T_{1}$
and
$T_{1}$
and
![]() $T_{2}$
, respectively. We say that
$T_{2}$
, respectively. We say that
![]() $q_{i}$
is nondegenerate to mean
$q_{i}$
is nondegenerate to mean
 $\det (T_{i})\neq 0$
. Define a partial order on the set of nondegenerate integral ternary quadratic forms by
$\det (T_{i})\neq 0$
. Define a partial order on the set of nondegenerate integral ternary quadratic forms by
![]() $q_{1}\leqslant q_{2}$
if there exists
$q_{1}\leqslant q_{2}$
if there exists
 $m\in M_{3}(\mathbf{Z})\cap \operatorname{GL}_{3}(\mathbf{Q})$
such that
$m\in M_{3}(\mathbf{Z})\cap \operatorname{GL}_{3}(\mathbf{Q})$
such that
 $T_{1}=m^{-1}T_{2}c(m)$
. Suppose
$T_{1}=m^{-1}T_{2}c(m)$
. Suppose
![]() $\unicode[STIX]{x1D6EC}_{i}$
is the even Clifford algebra associated to
$\unicode[STIX]{x1D6EC}_{i}$
is the even Clifford algebra associated to
 $q_{i}(x,y,z)$
. Then Lemma 3.8 implies that there is an injective ring map
$q_{i}(x,y,z)$
. Then Lemma 3.8 implies that there is an injective ring map
 $\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D6EC}_{2}$
if and only if
$\unicode[STIX]{x1D6EC}_{1}\rightarrow \unicode[STIX]{x1D6EC}_{2}$
if and only if
![]() $q_{1}\leqslant q_{2}$
.
$q_{1}\leqslant q_{2}$
.
4 A Dirichlet series for the spin
 $L$
-function
$L$
-function
In this section we combine Lemma 3.8 with a result of Evdokimov [Reference EvdokimovEvd84, Theorem 3] to give a Dirichlet series for the spin
![]() $L$
-function of level-one Siegel modular forms on
$L$
-function of level-one Siegel modular forms on
![]() $\operatorname{GSp}_{6}$
. Most of the work has already been done in [Reference EvdokimovEvd84]. Namely, [Reference EvdokimovEvd84, Theorem 3] very nearly gives a Dirichlet series for this
$\operatorname{GSp}_{6}$
. Most of the work has already been done in [Reference EvdokimovEvd84]. Namely, [Reference EvdokimovEvd84, Theorem 3] very nearly gives a Dirichlet series for this
![]() $L$
-function, except this result of Evdokimov involves an ‘error term’ that must be removed on the way to proving Theorem 1.2.Footnote
1
However, it turns out that this error term can be trivialized by applying the arithmetic invariant theory of ternary quadratic forms, in the form of Lemma 3.8, together with the fact that
$L$
-function, except this result of Evdokimov involves an ‘error term’ that must be removed on the way to proving Theorem 1.2.Footnote
1
However, it turns out that this error term can be trivialized by applying the arithmetic invariant theory of ternary quadratic forms, in the form of Lemma 3.8, together with the fact that
![]() $B_{0}$
is a maximal order. We first recall precisely [Reference EvdokimovEvd84, Theorem 3], and then apply Lemma 3.8 to obtain Corollary 4.2, which gives the desired Dirichlet series.
$B_{0}$
is a maximal order. We first recall precisely [Reference EvdokimovEvd84, Theorem 3], and then apply Lemma 3.8 to obtain Corollary 4.2, which gives the desired Dirichlet series.
To state [Reference EvdokimovEvd84, Theorem 3], we need to introduce some notation, largely following [Reference EvdokimovEvd84]. Denote by
![]() $P_{6}$
the Siegel parabolic of
$P_{6}$
the Siegel parabolic of
![]() $\operatorname{GSp}_{6}$
, i.e., the set of elements
$\operatorname{GSp}_{6}$
, i.e., the set of elements
![]() $(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!)$
in
$(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!)$
in
![]() $\operatorname{GSp}_{6}$
with
$\operatorname{GSp}_{6}$
with
![]() $C=0$
. Set
$C=0$
. Set
 $S_{p}=\{M\in \operatorname{GSp}_{6}(\mathbf{Z}[p^{-1}]):\unicode[STIX]{x1D708}(M)\in p^{\mathbf{Z}}\}$
,
$S_{p}=\{M\in \operatorname{GSp}_{6}(\mathbf{Z}[p^{-1}]):\unicode[STIX]{x1D708}(M)\in p^{\mathbf{Z}}\}$
,
 $\unicode[STIX]{x1D6E4}_{0}=\operatorname{Sp}_{6}(\mathbf{Z})\cap P_{6}(\mathbf{Q})$
, and
$\unicode[STIX]{x1D6E4}_{0}=\operatorname{Sp}_{6}(\mathbf{Z})\cap P_{6}(\mathbf{Q})$
, and
 $S_{0,p}=S_{p}\cap P_{6}(\mathbf{Q})$
. Denote by
$S_{0,p}=S_{p}\cap P_{6}(\mathbf{Q})$
. Denote by
![]() $L_{0,p}$
the double coset ring of
$L_{0,p}$
the double coset ring of
![]() $\unicode[STIX]{x1D6E4}_{0}$
in
$\unicode[STIX]{x1D6E4}_{0}$
in
![]() $S_{0,p}$
.
$S_{0,p}$
.
We define some elements of
![]() $L_{0,p}$
. Set
$L_{0,p}$
. Set
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{0}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p,p,p,1,1,1)\unicode[STIX]{x1D6E4}_{0}\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{1}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p,p,1,1,1,p)\unicode[STIX]{x1D6E4}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{0}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p,p,p,1,1,1)\unicode[STIX]{x1D6E4}_{0}\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{1}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p,p,1,1,1,p)\unicode[STIX]{x1D6E4}_{0}.\end{eqnarray}$$
Define
 $$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{2,0}^{0}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p^{2},p,p,1,p,p)\unicode[STIX]{x1D6E4}_{0}\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{3,0}^{0}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p,p,p,p,p,p)\unicode[STIX]{x1D6E4}_{0}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F1}_{2,0}^{0}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p^{2},p,p,1,p,p)\unicode[STIX]{x1D6E4}_{0}\quad \text{and}\quad \unicode[STIX]{x1D6F1}_{3,0}^{0}(p)=\unicode[STIX]{x1D6E4}_{0}\operatorname{diag}(p,p,p,p,p,p)\unicode[STIX]{x1D6E4}_{0}.\end{eqnarray}$$
For integers
 $0\leqslant r\leqslant i$
, set
$0\leqslant r\leqslant i$
, set
![]() $S_{i}^{r}$
to be the set of
$S_{i}^{r}$
to be the set of
 $A\in M_{i}(\mathbf{Z})$
with
$A\in M_{i}(\mathbf{Z})$
with
![]() $^{t}A=A$
, and
$^{t}A=A$
, and
 $\text{rank}_{\mathbf{F}_{p}}A=r$
. Define an equivalence relation on
$\text{rank}_{\mathbf{F}_{p}}A=r$
. Define an equivalence relation on
![]() $S_{i}^{r}$
by
$S_{i}^{r}$
by
![]() $A\sim A^{\prime }$
if there exists
$A\sim A^{\prime }$
if there exists
 $U\in \operatorname{GL}_{i}(\mathbf{Z})$
such that
$U\in \operatorname{GL}_{i}(\mathbf{Z})$
such that
 $A^{\prime }\equiv ^{t}UAU$
modulo
$A^{\prime }\equiv ^{t}UAU$
modulo
![]() $p$
. Now, define
$p$
. Now, define

where
 $A=(\!\begin{smallmatrix}a_{22} & a_{23}\\ a_{23} & a_{33}\end{smallmatrix}\!)$
. Similarly, define
$A=(\!\begin{smallmatrix}a_{22} & a_{23}\\ a_{23} & a_{33}\end{smallmatrix}\!)$
. Similarly, define

where
 $A=(a_{ij})$
. Set
$A=(a_{ij})$
. Set
 $\unicode[STIX]{x1D6F1}_{1}^{2}(p)=p(\unicode[STIX]{x1D6F1}_{2,0}^{1}(p)+\unicode[STIX]{x1D6F1}_{2,0}^{0}(p))$
and
$\unicode[STIX]{x1D6F1}_{1}^{2}(p)=p(\unicode[STIX]{x1D6F1}_{2,0}^{1}(p)+\unicode[STIX]{x1D6F1}_{2,0}^{0}(p))$
and
 $\unicode[STIX]{x1D6F1}_{1}^{3}(p)=p^{3}(\unicode[STIX]{x1D6F1}_{3,0}^{1}(p)+\unicode[STIX]{x1D6F1}_{3,0}^{0}(p))\unicode[STIX]{x1D6F1}_{0}(p)$
.
$\unicode[STIX]{x1D6F1}_{1}^{3}(p)=p^{3}(\unicode[STIX]{x1D6F1}_{3,0}^{1}(p)+\unicode[STIX]{x1D6F1}_{3,0}^{0}(p))\unicode[STIX]{x1D6F1}_{0}(p)$
.
Denote by
![]() ${\mathcal{F}}_{k}$
the space of holomorphic functions
${\mathcal{F}}_{k}$
the space of holomorphic functions
 $f:{\mathcal{H}}_{3}\rightarrow \mathbf{C}$
that satisfy
$f:{\mathcal{H}}_{3}\rightarrow \mathbf{C}$
that satisfy
 $f((AZ+B)D^{-1})=\det (D)^{k}f(Z)$
for all
$f((AZ+B)D^{-1})=\det (D)^{k}f(Z)$
for all
 $(\!\begin{smallmatrix}A & B\\ & D\end{smallmatrix}\!)\in P_{6}(\mathbf{Q})\cap \operatorname{Sp}_{6}(\mathbf{Z})$
. The ring
$(\!\begin{smallmatrix}A & B\\ & D\end{smallmatrix}\!)\in P_{6}(\mathbf{Q})\cap \operatorname{Sp}_{6}(\mathbf{Z})$
. The ring
![]() $L_{0,p}$
acts on
$L_{0,p}$
acts on
![]() ${\mathcal{F}}_{k}$
as follows. Suppose
${\mathcal{F}}_{k}$
as follows. Suppose
 $\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0}\subseteq S_{0,p}$
is a double coset. Then
$\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0}\subseteq S_{0,p}$
is a double coset. Then
![]() $\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0}$
has a single coset decomposition
$\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0}$
has a single coset decomposition
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0}=\bigsqcup _{i}\unicode[STIX]{x1D6E4}_{0}\left(\begin{array}{@{}cc@{}}A_{i} & B_{i}\\ & D_{i}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0}=\bigsqcup _{i}\unicode[STIX]{x1D6E4}_{0}\left(\begin{array}{@{}cc@{}}A_{i} & B_{i}\\ & D_{i}\end{array}\right),\end{eqnarray}$$
 $\unicode[STIX]{x1D708}((\!\begin{smallmatrix}A_{i} & B_{i}\\ & D_{i}\end{smallmatrix}\!))=p^{\unicode[STIX]{x1D6FF}_{i}}$
. One defines
$\unicode[STIX]{x1D708}((\!\begin{smallmatrix}A_{i} & B_{i}\\ & D_{i}\end{smallmatrix}\!))=p^{\unicode[STIX]{x1D6FF}_{i}}$
. One defines
 $$\begin{eqnarray}(f|\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0})(Z)=\mathop{\sum }_{i}p^{(3k-6)\unicode[STIX]{x1D6FF}_{i}}(\det (D_{i}))^{-k}f((A_{i}Z+B_{i})D_{i}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}(f|\unicode[STIX]{x1D6E4}_{0}h\unicode[STIX]{x1D6E4}_{0})(Z)=\mathop{\sum }_{i}p^{(3k-6)\unicode[STIX]{x1D6FF}_{i}}(\det (D_{i}))^{-k}f((A_{i}Z+B_{i})D_{i}^{-1}).\end{eqnarray}$$
Suppose
![]() $\unicode[STIX]{x1D719}$
is as in Definition 1.1, and
$\unicode[STIX]{x1D719}$
is as in Definition 1.1, and
 $f_{\unicode[STIX]{x1D719}}(Z)=\sum _{T^{\prime }>0}a(T^{\prime })e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(T^{\prime }Z)}$
is the associated level-one Siegel modular form. Let us write
$f_{\unicode[STIX]{x1D719}}(Z)=\sum _{T^{\prime }>0}a(T^{\prime })e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(T^{\prime }Z)}$
is the associated level-one Siegel modular form. Let us write
 $L_{\text{classical}}(\unicode[STIX]{x1D70B},\text{Spin},s)=L(\unicode[STIX]{x1D70B},\text{Spin},s-3r+3)$
for the classically normalized Spin
$L_{\text{classical}}(\unicode[STIX]{x1D70B},\text{Spin},s)=L(\unicode[STIX]{x1D70B},\text{Spin},s-3r+3)$
for the classically normalized Spin
![]() $L$
-function of
$L$
-function of
![]() $\unicode[STIX]{x1D70B}$
. Define
$\unicode[STIX]{x1D70B}$
. Define
 $Q_{p}^{1}(z)=1-\unicode[STIX]{x1D6F1}_{0}(p)z$
and
$Q_{p}^{1}(z)=1-\unicode[STIX]{x1D6F1}_{0}(p)z$
and
 $Q_{p}^{2}(z)=1-\unicode[STIX]{x1D6F1}_{1}(p)z+\unicode[STIX]{x1D6F1}_{1}^{2}(p)z^{2}-\unicode[STIX]{x1D6F1}_{1}^{3}(p)z^{3}$
, elements of
$Q_{p}^{2}(z)=1-\unicode[STIX]{x1D6F1}_{1}(p)z+\unicode[STIX]{x1D6F1}_{1}^{2}(p)z^{2}-\unicode[STIX]{x1D6F1}_{1}^{3}(p)z^{3}$
, elements of
![]() $L_{0,p}[z]$
, the polynomial ring over
$L_{0,p}[z]$
, the polynomial ring over
![]() $L_{0,p}$
in the indeterminate
$L_{0,p}$
in the indeterminate
![]() $z$
. For
$z$
. For
 $m\in \operatorname{GL}_{3}(\mathbf{Q})$
, define
$m\in \operatorname{GL}_{3}(\mathbf{Q})$
, define
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{T}(m)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if}~m^{-1}Tc(m)\in M_{3}(\mathbf{Z}),\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}_{T}(m)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if}~m^{-1}Tc(m)\in M_{3}(\mathbf{Z}),\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
The following theorem is essentially [Reference EvdokimovEvd84, Theorem 3].
Theorem 4.1 (Evdokimov).
Let the notations be as above. Set
![]() $M_{3}^{+}(\mathbf{Z})$
to be the elements of
$M_{3}^{+}(\mathbf{Z})$
to be the elements of
![]() $M_{3}(\mathbf{Z})$
with positive determinant. Then
$M_{3}(\mathbf{Z})$
with positive determinant. Then
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D706}\geqslant 1,m\in M_{3}^{+}(\mathbf{Z})/\!\operatorname{SL}_{3}(\mathbf{Z})}\frac{\unicode[STIX]{x1D6EF}_{T}(m)}{\unicode[STIX]{x1D706}^{s}\det (m)^{s-2r+3}}a(\unicode[STIX]{x1D706}m^{-1}Tc(m))=C_{f_{\unicode[STIX]{x1D719}}}(s,T)\frac{L_{\text{classical}}(\unicode[STIX]{x1D70B},\text{Spin},s)}{\unicode[STIX]{x1D701}_{D_{B}}(2s-6r+8)\unicode[STIX]{x1D701}(2s-6r+6)},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D706}\geqslant 1,m\in M_{3}^{+}(\mathbf{Z})/\!\operatorname{SL}_{3}(\mathbf{Z})}\frac{\unicode[STIX]{x1D6EF}_{T}(m)}{\unicode[STIX]{x1D706}^{s}\det (m)^{s-2r+3}}a(\unicode[STIX]{x1D706}m^{-1}Tc(m))=C_{f_{\unicode[STIX]{x1D719}}}(s,T)\frac{L_{\text{classical}}(\unicode[STIX]{x1D70B},\text{Spin},s)}{\unicode[STIX]{x1D701}_{D_{B}}(2s-6r+8)\unicode[STIX]{x1D701}(2s-6r+6)},\end{eqnarray}$$
where
 $$\begin{eqnarray}\unicode[STIX]{x1D701}_{D_{B}}(s)=\mathop{\prod }_{p<\infty ,p\nmid D_{B}}(1-p^{-s})^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D701}_{D_{B}}(s)=\mathop{\prod }_{p<\infty ,p\nmid D_{B}}(1-p^{-s})^{-1}\end{eqnarray}$$
and
 $C_{f_{\unicode[STIX]{x1D719}}}(s,T)$
is the
$C_{f_{\unicode[STIX]{x1D719}}}(s,T)$
is the
![]() $T$
th Fourier coefficient of
$T$
th Fourier coefficient of
 $$\begin{eqnarray}f_{\unicode[STIX]{x1D719}}\biggl|\mathop{\prod }_{p|4\det (T)}Q_{p}^{1}(p^{-s})Q_{p}^{2}(p^{-s}).\end{eqnarray}$$
$$\begin{eqnarray}f_{\unicode[STIX]{x1D719}}\biggl|\mathop{\prod }_{p|4\det (T)}Q_{p}^{1}(p^{-s})Q_{p}^{2}(p^{-s}).\end{eqnarray}$$
The function
 $C_{f_{\unicode[STIX]{x1D719}}}(s,T)$
in Theorem 4.1 is the ‘error term’ that we eluded to above. By applying Lemma 3.8, we will see that the hypothesis that
$C_{f_{\unicode[STIX]{x1D719}}}(s,T)$
in Theorem 4.1 is the ‘error term’ that we eluded to above. By applying Lemma 3.8, we will see that the hypothesis that
![]() $T$
corresponds to a maximal order implies that
$T$
corresponds to a maximal order implies that
 $C_{f_{\unicode[STIX]{x1D719}}}(s,T)=a(T)$
is independent of
$C_{f_{\unicode[STIX]{x1D719}}}(s,T)=a(T)$
is independent of
![]() $s$
. Hence under this assumption, the left-hand side of (4.1) yields a Dirichlet series for the Spin
$s$
. Hence under this assumption, the left-hand side of (4.1) yields a Dirichlet series for the Spin
![]() $L$
-function.
$L$
-function.
If
![]() ${\mathcal{O}}$
is an order in some quaternion algebra over
${\mathcal{O}}$
is an order in some quaternion algebra over
![]() $\mathbf{Q}$
ramified at infinity, then
$\mathbf{Q}$
ramified at infinity, then
 ${\mathcal{O}}=\unicode[STIX]{x1D6EC}_{T^{\prime }}$
is the even Clifford algebra associated to some half-integral, symmetric, positive-definite matrix
${\mathcal{O}}=\unicode[STIX]{x1D6EC}_{T^{\prime }}$
is the even Clifford algebra associated to some half-integral, symmetric, positive-definite matrix
![]() $T^{\prime }$
. We write
$T^{\prime }$
. We write
 $a({\mathcal{O}}):=a(T^{\prime })$
. Since
$a({\mathcal{O}}):=a(T^{\prime })$
. Since
 $a(T^{\prime })=a(k^{-1}T^{\prime }c(k))$
for
$a(T^{\prime })=a(k^{-1}T^{\prime }c(k))$
for
 $k\in \operatorname{SL}_{3}(\mathbf{Z})$
, the notation
$k\in \operatorname{SL}_{3}(\mathbf{Z})$
, the notation
![]() $a({\mathcal{O}})$
is independent of the choice of
$a({\mathcal{O}})$
is independent of the choice of
![]() $T^{\prime }$
, and thus well defined. We have the following corollary of Lemma 3.8 and Theorem 4.1.
$T^{\prime }$
, and thus well defined. We have the following corollary of Lemma 3.8 and Theorem 4.1.
Corollary 4.2. Suppose
![]() $\unicode[STIX]{x1D70B}$
is as in Definition 1.1,
$\unicode[STIX]{x1D70B}$
is as in Definition 1.1,
 $f_{\unicode[STIX]{x1D719}}(Z)=\sum _{T^{\prime }>0}a(T^{\prime })e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(T^{\prime }Z)}$
is the Fourier expansion of the associated Siegel modular form, and the even Clifford algebra
$f_{\unicode[STIX]{x1D719}}(Z)=\sum _{T^{\prime }>0}a(T^{\prime })e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(T^{\prime }Z)}$
is the Fourier expansion of the associated Siegel modular form, and the even Clifford algebra
![]() $B_{0}$
associated to
$B_{0}$
associated to
![]() $T$
is a maximal order in
$T$
is a maximal order in
 $B_{0}\otimes \mathbf{Q}$
. Then
$B_{0}\otimes \mathbf{Q}$
. Then
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D706}\geqslant 1,{\mathcal{O}}\subseteq B_{0}}\frac{a(\mathbf{Z}+\unicode[STIX]{x1D706}{\mathcal{O}})}{\unicode[STIX]{x1D706}^{s}[B_{0}:{\mathcal{O}}]^{s-2r+3}}=a(B_{0})\frac{L_{\text{classical}}(\unicode[STIX]{x1D70B},\text{Spin},s)}{\unicode[STIX]{x1D701}_{D_{B}}(2s-6r+8)\unicode[STIX]{x1D701}(2s-6r+6)},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D706}\geqslant 1,{\mathcal{O}}\subseteq B_{0}}\frac{a(\mathbf{Z}+\unicode[STIX]{x1D706}{\mathcal{O}})}{\unicode[STIX]{x1D706}^{s}[B_{0}:{\mathcal{O}}]^{s-2r+3}}=a(B_{0})\frac{L_{\text{classical}}(\unicode[STIX]{x1D70B},\text{Spin},s)}{\unicode[STIX]{x1D701}_{D_{B}}(2s-6r+8)\unicode[STIX]{x1D701}(2s-6r+6)},\end{eqnarray}$$
where
 $[B_{0}:{\mathcal{O}}]$
denotes the index of
$[B_{0}:{\mathcal{O}}]$
denotes the index of
![]() ${\mathcal{O}}$
in
${\mathcal{O}}$
in
![]() $B_{0}$
.
$B_{0}$
.
Proof. Applying Lemma 3.8, the left-hand side of (4.2) is seen to be equal to the left-hand side of (4.1).
The key point of the corollary is that, as mentioned above,
![]() $B_{0}$
being a maximal order implies
$B_{0}$
being a maximal order implies
 $C_{f_{\unicode[STIX]{x1D719}}}(s,T)=a(T)=a(B_{0})$
. To see this equality, consider the action of the operators
$C_{f_{\unicode[STIX]{x1D719}}}(s,T)=a(T)=a(B_{0})$
. To see this equality, consider the action of the operators
![]() $\unicode[STIX]{x1D6F1}_{0}(p)$
,
$\unicode[STIX]{x1D6F1}_{0}(p)$
,
![]() $\unicode[STIX]{x1D6F1}_{1}(p)$
,
$\unicode[STIX]{x1D6F1}_{1}(p)$
,
![]() $\unicode[STIX]{x1D6F1}_{1}^{2}(p)$
and
$\unicode[STIX]{x1D6F1}_{1}^{2}(p)$
and
![]() $\unicode[STIX]{x1D6F1}_{1}^{3}(p)$
on the Fourier coefficients of
$\unicode[STIX]{x1D6F1}_{1}^{3}(p)$
on the Fourier coefficients of
![]() $f_{\unicode[STIX]{x1D719}}$
. Suppose
$f_{\unicode[STIX]{x1D719}}$
. Suppose
![]() $\unicode[STIX]{x1D6F1}(p)$
is one of these operators. For a quaternion order
$\unicode[STIX]{x1D6F1}(p)$
is one of these operators. For a quaternion order
![]() ${\mathcal{O}}$
and a Siegel modular form
${\mathcal{O}}$
and a Siegel modular form
![]() $f$
, set
$f$
, set
 $a({\mathcal{O}},f|\unicode[STIX]{x1D6F1}(p))$
the
$a({\mathcal{O}},f|\unicode[STIX]{x1D6F1}(p))$
the
![]() ${\mathcal{O}}$
Fourier coefficient of
${\mathcal{O}}$
Fourier coefficient of
![]() $f|\unicode[STIX]{x1D6F1}(p)$
. Applying Lemma 3.8, one verifies that
$f|\unicode[STIX]{x1D6F1}(p)$
. Applying Lemma 3.8, one verifies that
 $a({\mathcal{O}},f|\unicode[STIX]{x1D6F1}(p))$
is a linear combination of
$a({\mathcal{O}},f|\unicode[STIX]{x1D6F1}(p))$
is a linear combination of
 $a({\mathcal{O}}^{\prime },f)$
for certain orders
$a({\mathcal{O}}^{\prime },f)$
for certain orders
![]() ${\mathcal{O}}^{\prime }\supseteq {\mathcal{O}}$
with
${\mathcal{O}}^{\prime }\supseteq {\mathcal{O}}$
with
 $[{\mathcal{O}}^{\prime }:{\mathcal{O}}]=p,p^{2}$
or
$[{\mathcal{O}}^{\prime }:{\mathcal{O}}]=p,p^{2}$
or
![]() $p^{3}$
. Since
$p^{3}$
. Since
![]() $B_{0}$
is a maximal order,
$B_{0}$
is a maximal order,
 $a(B_{0},f|\unicode[STIX]{x1D6F1}(p))=0$
, and the equality
$a(B_{0},f|\unicode[STIX]{x1D6F1}(p))=0$
, and the equality
 $C_{f_{\unicode[STIX]{x1D719}}}(s,T)=a(B_{0})$
follows.◻
$C_{f_{\unicode[STIX]{x1D719}}}(s,T)=a(B_{0})$
follows.◻
Remark 4.3. In [Reference EvdokimovEvd84, Theorem 4], Evdokimov also uses his result [Reference EvdokimovEvd84, Theorem 3] to obtain a Dirichlet series for the Spin
![]() $L$
-function, but only under the assumption that
$L$
-function, but only under the assumption that
![]() $f_{\unicode[STIX]{x1D719}}$
satisfies
$f_{\unicode[STIX]{x1D719}}$
satisfies
 $a(T^{\prime })=0$
for all
$a(T^{\prime })=0$
for all
![]() $T^{\prime }$
with
$T^{\prime }$
with
 $4\det (T^{\prime })$
strictly dividing
$4\det (T^{\prime })$
strictly dividing
 $4\det (T)$
.
$4\det (T)$
.
5 The Rankin–Selberg integral
In this section we define the map
 $\operatorname{GSp}_{6}\rightarrow \text{G}$
and the Eisenstein series on
$\operatorname{GSp}_{6}\rightarrow \text{G}$
and the Eisenstein series on
![]() $\text{G}$
. We also give the global Rankin–Selberg convolution and unfold it.
$\text{G}$
. We also give the global Rankin–Selberg convolution and unfold it.
5.1 Construction of global integral
We first embed
![]() $\operatorname{GSp}_{6}$
into
$\operatorname{GSp}_{6}$
into
![]() $\text{G}$
, preserving the similitude. Denote by
$\text{G}$
, preserving the similitude. Denote by
![]() $W_{6}$
the defining six-dimensional representation of
$W_{6}$
the defining six-dimensional representation of
![]() $\operatorname{GSp}_{6}$
, and
$\operatorname{GSp}_{6}$
, and
![]() $\langle \;,\;\rangle$
the invariant symplectic form. We let
$\langle \;,\;\rangle$
the invariant symplectic form. We let
![]() $\operatorname{GSp}_{6}$
act on
$\operatorname{GSp}_{6}$
act on
![]() $W_{6}$
on the right. In matrices,
$W_{6}$
on the right. In matrices,
![]() $\operatorname{GSp}_{6}$
is the set of
$\operatorname{GSp}_{6}$
is the set of
 $g\in \operatorname{GL}_{6}$
satisfying
$g\in \operatorname{GL}_{6}$
satisfying
 $gJ_{6}\text{}^{t}g=\unicode[STIX]{x1D708}(g)J_{6}$
, where
$gJ_{6}\text{}^{t}g=\unicode[STIX]{x1D708}(g)J_{6}$
, where
 $J_{6}=(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!)$
and the similitude
$J_{6}=(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!)$
and the similitude
 $\unicode[STIX]{x1D708}(g)\in \operatorname{GL}_{1}$
. The action of
$\unicode[STIX]{x1D708}(g)\in \operatorname{GL}_{1}$
. The action of
![]() $\operatorname{GSp}_{6}$
on
$\operatorname{GSp}_{6}$
on
![]() $W_{6}$
is then the usual right action of matrices on row vectors.
$W_{6}$
is then the usual right action of matrices on row vectors.
Pick a symplectic basis
 $e_{1},e_{2},e_{3},f_{1},f_{2},f_{3}$
of
$e_{1},e_{2},e_{3},f_{1},f_{2},f_{3}$
of
![]() $W_{6}$
; that is,
$W_{6}$
; that is,
 $\langle e_{i},f_{j}\rangle =\unicode[STIX]{x1D6FF}_{ij}$
. We fix a quaternion algebra
$\langle e_{i},f_{j}\rangle =\unicode[STIX]{x1D6FF}_{ij}$
. We fix a quaternion algebra
![]() $B$
over
$B$
over
![]() $\mathbf{Q}$
that is ramified at infinity. For such a
$\mathbf{Q}$
that is ramified at infinity. For such a
![]() $B$
, denote by
$B$
, denote by
 $W=\mathbf{Q}\,\oplus \,H_{3}(B)\oplus H_{3}(B)\oplus \mathbf{Q}$
Freudenthal’s space, as considered in § 2. Now consider the linear map
$W=\mathbf{Q}\,\oplus \,H_{3}(B)\oplus H_{3}(B)\oplus \mathbf{Q}$
Freudenthal’s space, as considered in § 2. Now consider the linear map
 $W\rightarrow (\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1})\otimes _{\mathbf{Q}}B$
defined as follows: set
$W\rightarrow (\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1})\otimes _{\mathbf{Q}}B$
defined as follows: set
 $e_{i}^{\ast }=e_{i+1}\wedge e_{i+2}$
and
$e_{i}^{\ast }=e_{i+1}\wedge e_{i+2}$
and
 $f_{i}^{\ast }=f_{i+1}\wedge f_{i+2}$
with the indices taken modulo 3. Then we map
$f_{i}^{\ast }=f_{i+1}\wedge f_{i+2}$
with the indices taken modulo 3. Then we map
 $(a,b,c,d)$
in
$(a,b,c,d)$
in
![]() $W$
to
$W$
to
 $$\begin{eqnarray}ae_{1}\wedge e_{2}\wedge e_{3}+\biggl(\mathop{\sum }_{i,j}b_{ij}e_{i}^{\ast }\wedge f_{j}\biggr)+\biggl(\mathop{\sum }_{i,j}c_{ij}f_{i}^{\ast }\wedge e_{j}\biggr)+df_{1}\wedge f_{2}\wedge f_{3}.\end{eqnarray}$$
$$\begin{eqnarray}ae_{1}\wedge e_{2}\wedge e_{3}+\biggl(\mathop{\sum }_{i,j}b_{ij}e_{i}^{\ast }\wedge f_{j}\biggr)+\biggl(\mathop{\sum }_{i,j}c_{ij}f_{i}^{\ast }\wedge e_{j}\biggr)+df_{1}\wedge f_{2}\wedge f_{3}.\end{eqnarray}$$
With this definition, and the natural action of
![]() $\operatorname{GSp}_{6}$
on
$\operatorname{GSp}_{6}$
on
 $\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1}$
,
$\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1}$
,
![]() $\operatorname{GSp}_{6}$
preserves the image of
$\operatorname{GSp}_{6}$
preserves the image of
![]() $W$
, and preserves the symplectic and quartic form on
$W$
, and preserves the symplectic and quartic form on
![]() $W$
, up to similitude. These facts are checked in the following lemma.
$W$
, up to similitude. These facts are checked in the following lemma.
Lemma 5.1. Identify
![]() $W$
with its image in
$W$
with its image in
 $(\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1})\otimes _{\mathbf{Q}}B$
. Then, the element
$(\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1})\otimes _{\mathbf{Q}}B$
. Then, the element
![]() $(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!)$
of
$(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!)$
of
![]() $\operatorname{GSp}_{6}$
acts on
$\operatorname{GSp}_{6}$
acts on
![]() $W$
as
$W$
as
![]() $n(X)$
, and the element
$n(X)$
, and the element
![]() $(\!\begin{smallmatrix}0 & 1\\ -1 & 0\end{smallmatrix}\!)$
acts on
$(\!\begin{smallmatrix}0 & 1\\ -1 & 0\end{smallmatrix}\!)$
acts on
![]() $W$
via
$W$
via
 $(a,b,c,d)\mapsto (-d,c,-b,a)$
. If
$(a,b,c,d)\mapsto (-d,c,-b,a)$
. If
 $(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)\in \operatorname{GSp}_{6}$
has similitude
$(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)\in \operatorname{GSp}_{6}$
has similitude
![]() $\unicode[STIX]{x1D708}$
, then
$\unicode[STIX]{x1D708}$
, then
 $$\begin{eqnarray}(a,b,c,d)(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)=\unicode[STIX]{x1D708}^{-1}(\det (m)a,\det (m)m^{-1}bn,\det (n)n^{-1}cm,\det (n)\,d).\end{eqnarray}$$
$$\begin{eqnarray}(a,b,c,d)(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)=\unicode[STIX]{x1D708}^{-1}(\det (m)a,\det (m)m^{-1}bn,\det (n)n^{-1}cm,\det (n)\,d).\end{eqnarray}$$
It follows that the inclusion
 $W\rightarrow (\bigwedge ^{3}W_{6}\,\otimes \,\unicode[STIX]{x1D708}^{-1})\,\otimes _{\mathbf{Q}}B$
induces an inclusion
$W\rightarrow (\bigwedge ^{3}W_{6}\,\otimes \,\unicode[STIX]{x1D708}^{-1})\,\otimes _{\mathbf{Q}}B$
induces an inclusion
 $\operatorname{GSp}_{6}\rightarrow \text{G}$
, preserving similitudes.
$\operatorname{GSp}_{6}\rightarrow \text{G}$
, preserving similitudes.
Proof. The formula for the action of
![]() $(\!\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\!)$
is immediate. We check some of the other formulas.
$(\!\begin{smallmatrix} & 1\\ -1 & \end{smallmatrix}\!)$
is immediate. We check some of the other formulas.
Consider the action of
![]() $(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)$
. One first computes that under the action of
$(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)$
. One first computes that under the action of
![]() $m$
,
$m$
,
 $e_{i}^{\ast }\mapsto \sum _{j}c(m)_{ij}e_{j}^{\ast }$
, where
$e_{i}^{\ast }\mapsto \sum _{j}c(m)_{ij}e_{j}^{\ast }$
, where
 $c(m)=\det (m)\text{}^{t}m^{-1}$
is the cofactor matrix of
$c(m)=\det (m)\text{}^{t}m^{-1}$
is the cofactor matrix of
![]() $m$
. Ignoring the twist by the similitude
$m$
. Ignoring the twist by the similitude
![]() $\unicode[STIX]{x1D708}^{-1}$
in
$\unicode[STIX]{x1D708}^{-1}$
in
 $\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1}$
, one then obtains
$\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1}$
, one then obtains
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i,j}b_{ij}e_{i}^{\ast }\wedge f_{j} & \mapsto & \displaystyle \mathop{\sum }_{i,j,t,s}b_{ij}c(m)_{it}n_{js}e_{t}^{\ast }\wedge f_{s}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{t,s}(\text{}^{t}c(m)bn)_{ts}e_{t}^{\ast }\wedge f_{s}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i,j}b_{ij}e_{i}^{\ast }\wedge f_{j} & \mapsto & \displaystyle \mathop{\sum }_{i,j,t,s}b_{ij}c(m)_{it}n_{js}e_{t}^{\ast }\wedge f_{s}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{t,s}(\text{}^{t}c(m)bn)_{ts}e_{t}^{\ast }\wedge f_{s}.\nonumber\end{eqnarray}$$
This proves the formula for the action of
![]() $(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)$
on the
$(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)$
on the
![]() $b$
values of
$b$
values of
 $(a,b,c,d)$
. The action on the
$(a,b,c,d)$
. The action on the
![]() $c$
values is similar, and the action on the
$c$
values is similar, and the action on the
![]() $a$
values and
$a$
values and
![]() $b$
values are trivial.
$b$
values are trivial.
For
![]() $X$
in
$X$
in
![]() $H_{3}(B)$
, denote by
$H_{3}(B)$
, denote by
![]() $L(X)$
the logarithm, inside
$L(X)$
the logarithm, inside
 $\text{End}(W)$
, of the element
$\text{End}(W)$
, of the element
![]() $n(X)$
of
$n(X)$
of
![]() $\operatorname{GL}(W)$
. That is, set
$\operatorname{GL}(W)$
. That is, set
 $L(X)=\sum _{m\geqslant 1}(-1)^{m-1}((n(X)-1)^{m}/m)$
. From the definition (2.5) of
$L(X)=\sum _{m\geqslant 1}(-1)^{m-1}((n(X)-1)^{m}/m)$
. From the definition (2.5) of
![]() $n(X)$
, one sees
$n(X)$
, one sees
 $(n(X)-1)^{4}=0$
, and thus the sum defining
$(n(X)-1)^{4}=0$
, and thus the sum defining
![]() $L(X)$
terminates after four terms. One gets
$L(X)$
terminates after four terms. One gets
 $$\begin{eqnarray}(a,b,c,d)L(X)=(0,aX,b\times X,\operatorname{tr}(c,X))\end{eqnarray}$$
$$\begin{eqnarray}(a,b,c,d)L(X)=(0,aX,b\times X,\operatorname{tr}(c,X))\end{eqnarray}$$
and
 $n(X)=1+L(X)+L(X)^{2}/2+L(X)^{3}/6$
.
$n(X)=1+L(X)+L(X)^{2}/2+L(X)^{3}/6$
.
Similarly, for
![]() $(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!)$
in
$(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!)$
in
![]() $\operatorname{GSp}_{6}$
, denote by
$\operatorname{GSp}_{6}$
, denote by
![]() $n_{6}(X)$
its action on
$n_{6}(X)$
its action on
![]() $W_{6}$
,
$W_{6}$
,
![]() $n^{\prime }(X)$
its action on
$n^{\prime }(X)$
its action on
 $(\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1})\otimes B$
, and
$(\bigwedge ^{3}W_{6}\otimes \unicode[STIX]{x1D708}^{-1})\otimes B$
, and
![]() $L_{6}(X)$
, respectively
$L_{6}(X)$
, respectively
![]() $L^{\prime }(X)$
, the logarithms of these actions. Since
$L^{\prime }(X)$
, the logarithms of these actions. Since
 $n_{6}(X)=1+L_{6}(X)$
, and the action of
$n_{6}(X)=1+L_{6}(X)$
, and the action of
![]() $n(X)$
on
$n(X)$
on
![]() $\bigwedge ^{3}W_{6}$
is defined by cubic polynomials in the entries of
$\bigwedge ^{3}W_{6}$
is defined by cubic polynomials in the entries of
![]() $(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!)$
, one obtains
$(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!)$
, one obtains
 $n^{\prime }(X)=1+L^{\prime }(X)+L^{\prime }(X)^{2}/2+L^{\prime }(X)^{3}/6.$
Hence to check that
$n^{\prime }(X)=1+L^{\prime }(X)+L^{\prime }(X)^{2}/2+L^{\prime }(X)^{3}/6.$
Hence to check that
![]() $n^{\prime }(X)$
restricts to
$n^{\prime }(X)$
restricts to
![]() $n(X)$
on
$n(X)$
on
![]() $W$
, it suffices to check the analogous statement for
$W$
, it suffices to check the analogous statement for
![]() $L^{\prime }(X)$
and
$L^{\prime }(X)$
and
![]() $L(X)$
.
$L(X)$
.
So, suppose
![]() $X$
is a
$X$
is a
![]() $3\times 3$
symmetric matrix. We consider the action
$3\times 3$
symmetric matrix. We consider the action
 $(0,b,0,0)L^{\prime }(X)$
. One has
$(0,b,0,0)L^{\prime }(X)$
. One has
 $$\begin{eqnarray}(e_{i}^{\ast }\wedge f_{j})L^{\prime }(X)=\mathop{\sum }_{k}X_{i+1,k}f_{k}\wedge e_{i+2}\wedge f_{j}+X_{i+2,k}e_{i+1}\wedge f_{k}\wedge f_{j},\end{eqnarray}$$
$$\begin{eqnarray}(e_{i}^{\ast }\wedge f_{j})L^{\prime }(X)=\mathop{\sum }_{k}X_{i+1,k}f_{k}\wedge e_{i+2}\wedge f_{j}+X_{i+2,k}e_{i+1}\wedge f_{k}\wedge f_{j},\end{eqnarray}$$
where
![]() $X_{a,b}$
denotes the
$X_{a,b}$
denotes the
![]() $a,b$
matrix entry of
$a,b$
matrix entry of
![]() $X$
. Hence
$X$
. Hence
 $$\begin{eqnarray}\displaystyle \biggl(\mathop{\sum }_{ij}b_{ij}e_{i}^{\ast }\wedge f_{j}\biggr)L^{\prime }(X) & = & \displaystyle \mathop{\sum }_{j,k,\ell }(b_{\ell +1,j}X_{\ell -1,k}-X_{\ell +1,k}b_{\ell -1,j})f_{j}\wedge f_{k}\wedge e_{\ell }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}V_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}f_{\unicode[STIX]{x1D6FC}}^{\ast }\wedge e_{\unicode[STIX]{x1D6FD}}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl(\mathop{\sum }_{ij}b_{ij}e_{i}^{\ast }\wedge f_{j}\biggr)L^{\prime }(X) & = & \displaystyle \mathop{\sum }_{j,k,\ell }(b_{\ell +1,j}X_{\ell -1,k}-X_{\ell +1,k}b_{\ell -1,j})f_{j}\wedge f_{k}\wedge e_{\ell }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}V_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}f_{\unicode[STIX]{x1D6FC}}^{\ast }\wedge e_{\unicode[STIX]{x1D6FD}}\end{eqnarray}$$
for some element
![]() $V$
of
$V$
of
![]() $M_{3}(B)$
. For a general element
$M_{3}(B)$
. For a general element
![]() $Y$
of
$Y$
of
![]() $M_{3}(B)$
, denote by
$M_{3}(B)$
, denote by
 $c_{i}(Y),a_{i}(Y),a_{i}(Y)^{\prime }$
the coordinates of
$c_{i}(Y),a_{i}(Y),a_{i}(Y)^{\prime }$
the coordinates of
![]() $Y$
:
$Y$
:
 $$\begin{eqnarray}Y=\left(\begin{array}{@{}ccc@{}}c_{1}(Y) & a_{3}(Y) & a_{2}(Y)^{\prime }\\ a_{3}(Y)^{\prime } & c_{2}(Y) & a_{1}(Y)\\ a_{2}(Y) & a_{1}(Y)^{\prime } & c_{3}(Y)\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}Y=\left(\begin{array}{@{}ccc@{}}c_{1}(Y) & a_{3}(Y) & a_{2}(Y)^{\prime }\\ a_{3}(Y)^{\prime } & c_{2}(Y) & a_{1}(Y)\\ a_{2}(Y) & a_{1}(Y)^{\prime } & c_{3}(Y)\end{array}\right).\end{eqnarray}$$
Then (5.1) yields
 $$\begin{eqnarray}\begin{array}{@{}rcl@{}}c_{t}(V)\ & =\ & c_{t-1}(X)c_{t+1}(b)+c_{t+1}(X)c_{t-1}(b)-(a_{t}(X),a_{t}(b)),\\ a_{t}(V)\ & =\ & a_{t+1}^{\prime }(b)a_{t-1}^{\prime }(X)+a_{t+1}^{\prime }(X)a_{t-1}^{\prime }(b)-(c_{t}(X)a_{t}(b)+c_{t}(b)a_{t}(X)),\\ a_{t}^{\prime }(V)\ & =\ & a_{t+1}(b)a_{t-1}(X)+a_{t+1}(X)a_{t-1}(b)-(c_{t}(X)a_{t}^{\prime }(b)+c_{t}(b)a_{t}^{\prime }(X)).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}c_{t}(V)\ & =\ & c_{t-1}(X)c_{t+1}(b)+c_{t+1}(X)c_{t-1}(b)-(a_{t}(X),a_{t}(b)),\\ a_{t}(V)\ & =\ & a_{t+1}^{\prime }(b)a_{t-1}^{\prime }(X)+a_{t+1}^{\prime }(X)a_{t-1}^{\prime }(b)-(c_{t}(X)a_{t}(b)+c_{t}(b)a_{t}(X)),\\ a_{t}^{\prime }(V)\ & =\ & a_{t+1}(b)a_{t-1}(X)+a_{t+1}(X)a_{t-1}(b)-(c_{t}(X)a_{t}^{\prime }(b)+c_{t}(b)a_{t}^{\prime }(X)).\end{array}\end{eqnarray}$$
The indices in (5.2) are taken modulo 3. Linearizing (2.3) for the map
![]() $\#$
yields exactly the formulas (5.2), and thus
$\#$
yields exactly the formulas (5.2), and thus
 $V=b\times X$
. Hence
$V=b\times X$
. Hence
 $(0,b,0,0)L^{\prime }(X)=(0,0,b\times X,0)$
.
$(0,b,0,0)L^{\prime }(X)=(0,0,b\times X,0)$
.
The formulas
 $(a,0,0,0)L^{\prime }(X)=(0,aX,0,0)$
and
$(a,0,0,0)L^{\prime }(X)=(0,aX,0,0)$
and
 $(0,0,c,d)L^{\prime }(X)=(0,0,0,\operatorname{tr}(c,X))$
are much easier to establish. Hence
$(0,0,c,d)L^{\prime }(X)=(0,0,0,\operatorname{tr}(c,X))$
are much easier to establish. Hence
![]() $L^{\prime }(X)$
preserves
$L^{\prime }(X)$
preserves
![]() $W$
, and restricts to the action of
$W$
, and restricts to the action of
![]() $L(X)$
. This completes the proof of the lemma.◻
$L(X)$
. This completes the proof of the lemma.◻
We need to define an integral structure on
![]() $W$
. To do this, first we fix a maximal order
$W$
. To do this, first we fix a maximal order
![]() $B_{0}$
in
$B_{0}$
in
![]() $B$
. Then
$B$
. Then
 $$\begin{eqnarray}W(\mathbf{Z}):=W(\mathbf{Q})\cap \{(\wedge ^{3}W_{6}(\mathbf{Z})\otimes \unicode[STIX]{x1D708}^{-1})\otimes _{\boldsymbol{ Z}}B_{0}\},\end{eqnarray}$$
$$\begin{eqnarray}W(\mathbf{Z}):=W(\mathbf{Q})\cap \{(\wedge ^{3}W_{6}(\mathbf{Z})\otimes \unicode[STIX]{x1D708}^{-1})\otimes _{\boldsymbol{ Z}}B_{0}\},\end{eqnarray}$$
and for a finite prime
![]() $p$
,
$p$
,
 $W(\mathbf{Z}_{p}):=W(\mathbf{Z})\otimes \mathbf{Z}_{p}$
. Define
$W(\mathbf{Z}_{p}):=W(\mathbf{Z})\otimes \mathbf{Z}_{p}$
. Define
![]() $J_{0}$
to be the lattice in
$J_{0}$
to be the lattice in
![]() $H_{3}(B)$
consisting of those
$H_{3}(B)$
consisting of those
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}c_{1} & x_{3} & x_{2}^{\ast }\\ x_{3}^{\ast } & c_{2} & x_{1}\\ x_{2} & x_{1}^{\ast } & c_{3}\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}c_{1} & x_{3} & x_{2}^{\ast }\\ x_{3}^{\ast } & c_{2} & x_{1}\\ x_{2} & x_{1}^{\ast } & c_{3}\end{array}\right)\end{eqnarray}$$
with
![]() $c_{i}\in \mathbf{Z}$
and
$c_{i}\in \mathbf{Z}$
and
![]() $x_{i}\in B_{0}$
. Then
$x_{i}\in B_{0}$
. Then
 $(a,b,c,d)\in W(\mathbf{Q})$
is in
$(a,b,c,d)\in W(\mathbf{Q})$
is in
![]() $W(\mathbf{Z})$
if and only if
$W(\mathbf{Z})$
if and only if
 $a,d\in \mathbf{Z}$
and
$a,d\in \mathbf{Z}$
and
 $b,c\in J_{0}$
. It is clear from (5.3) that
$b,c\in J_{0}$
. It is clear from (5.3) that
 $\operatorname{GSp}_{6}(\mathbf{Z}_{p})$
stabilizes
$\operatorname{GSp}_{6}(\mathbf{Z}_{p})$
stabilizes
![]() $W(\mathbf{Z}_{p})$
for all finite primes
$W(\mathbf{Z}_{p})$
for all finite primes
![]() $p$
.
$p$
.
We now define the Eisenstein series on
![]() $\text{G}$
. Recall the rank-one element
$\text{G}$
. Recall the rank-one element
 $f=(0,0,0,1)$
of
$f=(0,0,0,1)$
of
![]() $W$
. Denote by
$W$
. Denote by
![]() $P$
the parabolic subgroup of
$P$
the parabolic subgroup of
![]() $\text{G}$
stabilizing the line
$\text{G}$
stabilizing the line
![]() $\mathbf{Q}f$
. The Eisenstein series will be associated to a character of
$\mathbf{Q}f$
. The Eisenstein series will be associated to a character of
![]() $P$
. To define this Eisenstein series, we select a particular Schwartz–Bruhat function
$P$
. To define this Eisenstein series, we select a particular Schwartz–Bruhat function
 $\unicode[STIX]{x1D6F7}=\prod _{v}\unicode[STIX]{x1D6F7}_{v}$
on
$\unicode[STIX]{x1D6F7}=\prod _{v}\unicode[STIX]{x1D6F7}_{v}$
on
![]() $W(\mathbf{A})$
. At finite primes,
$W(\mathbf{A})$
. At finite primes,
![]() $\unicode[STIX]{x1D6F7}_{p}$
is the characteristic function of
$\unicode[STIX]{x1D6F7}_{p}$
is the characteristic function of
![]() $W(\mathbf{Z}_{p})$
. In § 6.2 will define a Schwartz function
$W(\mathbf{Z}_{p})$
. In § 6.2 will define a Schwartz function
![]() $\unicode[STIX]{x1D6F7}_{\infty ,2r}$
on
$\unicode[STIX]{x1D6F7}_{\infty ,2r}$
on
![]() $W(\mathbf{R})$
that is appropriate for cusp forms
$W(\mathbf{R})$
that is appropriate for cusp forms
![]() $\unicode[STIX]{x1D719}$
that correspond to a Siegel modular form of weight
$\unicode[STIX]{x1D719}$
that correspond to a Siegel modular form of weight
![]() $2r$
. The Schwartz function
$2r$
. The Schwartz function
![]() $\unicode[STIX]{x1D6F7}_{\infty ,2r}$
will be a Gaussian times a polynomial of degree
$\unicode[STIX]{x1D6F7}_{\infty ,2r}$
will be a Gaussian times a polynomial of degree
![]() $2r$
. We set
$2r$
. We set
 $$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}}(g,s)=|\unicode[STIX]{x1D708}(g)|^{s}\int _{\operatorname{GL}_{1}(\mathbf{A})}\unicode[STIX]{x1D6F7}(tfg)|t|^{2s}\,dt,\end{eqnarray}$$
$$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}}(g,s)=|\unicode[STIX]{x1D708}(g)|^{s}\int _{\operatorname{GL}_{1}(\mathbf{A})}\unicode[STIX]{x1D6F7}(tfg)|t|^{2s}\,dt,\end{eqnarray}$$
and
 $$\begin{eqnarray}E^{\unicode[STIX]{x1D6F7}}(g,s)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \!\text{G}(\mathbf{Q})}f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g,s).\end{eqnarray}$$
$$\begin{eqnarray}E^{\unicode[STIX]{x1D6F7}}(g,s)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \!\text{G}(\mathbf{Q})}f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g,s).\end{eqnarray}$$
This is not yet the normalized Eisenstein series. Assume
![]() $\unicode[STIX]{x1D6F7}_{\infty ,2r}$
is chosen as in § 6.2, and denote by
$\unicode[STIX]{x1D6F7}_{\infty ,2r}$
is chosen as in § 6.2, and denote by
 $D_{B}=\prod _{p<\infty ,\text{ramified}}p$
the product of the finite primes ramified in
$D_{B}=\prod _{p<\infty ,\text{ramified}}p$
the product of the finite primes ramified in
![]() $B$
. Then the normalized Eisenstein series is
$B$
. Then the normalized Eisenstein series is
 $$\begin{eqnarray}\displaystyle E_{2r}^{\ast }(g,s) & = & \displaystyle \unicode[STIX]{x1D70B}^{-(s+r)}D_{B}^{s}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-8)\biggl(\mathop{\prod }_{p<\infty ~\text{split}}\unicode[STIX]{x1D701}_{p}(2s-2)\unicode[STIX]{x1D701}_{p}(2s-4)\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{p<\infty ~\text{ramified}}\unicode[STIX]{x1D701}_{p}(2s-4)\biggr)E^{\unicode[STIX]{x1D6F7}}(g,s).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{2r}^{\ast }(g,s) & = & \displaystyle \unicode[STIX]{x1D70B}^{-(s+r)}D_{B}^{s}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-8)\biggl(\mathop{\prod }_{p<\infty ~\text{split}}\unicode[STIX]{x1D701}_{p}(2s-2)\unicode[STIX]{x1D701}_{p}(2s-4)\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{p<\infty ~\text{ramified}}\unicode[STIX]{x1D701}_{p}(2s-4)\biggr)E^{\unicode[STIX]{x1D6F7}}(g,s).\nonumber\end{eqnarray}$$
Here, as usual,
 $\unicode[STIX]{x1D6E4}_{\mathbf{R}}(s)=\unicode[STIX]{x1D70B}^{-s/2}\unicode[STIX]{x1D6E4}(s/2)$
. The following theorem is proved in § 7.
$\unicode[STIX]{x1D6E4}_{\mathbf{R}}(s)=\unicode[STIX]{x1D70B}^{-s/2}\unicode[STIX]{x1D6E4}(s/2)$
. The following theorem is proved in § 7.
Theorem 5.2. The Eisenstein series
 $E_{2r}^{\ast }(g,s)$
has finitely many poles, all contained in the set
$E_{2r}^{\ast }(g,s)$
has finitely many poles, all contained in the set
 $\frac{1}{2}\mathbf{Z}\cap [0,5]$
, and satisfies the functional equation
$\frac{1}{2}\mathbf{Z}\cap [0,5]$
, and satisfies the functional equation
 $E_{2r}^{\ast }(g,s)=E_{2r}^{\ast }(g,5-s)$
.
$E_{2r}^{\ast }(g,s)=E_{2r}^{\ast }(g,5-s)$
.
For a cusp form
![]() $\unicode[STIX]{x1D719}$
associated to a level-one, holomorphic Siegel modular form of weight
$\unicode[STIX]{x1D719}$
associated to a level-one, holomorphic Siegel modular form of weight
![]() $2r$
, the global integral is
$2r$
, the global integral is
 $$\begin{eqnarray}I_{2r}^{\ast }(\unicode[STIX]{x1D719},s)=\int _{\operatorname{ GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)E_{2r}^{\ast }(g,s)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}I_{2r}^{\ast }(\unicode[STIX]{x1D719},s)=\int _{\operatorname{ GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)E_{2r}^{\ast }(g,s)\,dg.\end{eqnarray}$$
By Theorem 5.2,
 $I_{2r}^{\ast }(\unicode[STIX]{x1D719},s)=I_{2r}^{\ast }(\unicode[STIX]{x1D719},5-s)$
.
$I_{2r}^{\ast }(\unicode[STIX]{x1D719},s)=I_{2r}^{\ast }(\unicode[STIX]{x1D719},5-s)$
.
Remark 5.3. This is the first place where defining the group
![]() $\text{G}$
in terms of the Freudenthal construction gives one a substantial technical advantage. Namely, because we have defined
$\text{G}$
in terms of the Freudenthal construction gives one a substantial technical advantage. Namely, because we have defined
![]() $\text{G}$
in terms of the representation
$\text{G}$
in terms of the representation
![]() $W$
, we were able to construct the Eisenstein section
$W$
, we were able to construct the Eisenstein section
![]() $f^{\unicode[STIX]{x1D6F7}}$
in terms of a characteristic function on
$f^{\unicode[STIX]{x1D6F7}}$
in terms of a characteristic function on
![]() $W$
. We will see in § 6 that this definition plays a significant role in easing the computation.
$W$
. We will see in § 6 that this definition plays a significant role in easing the computation.
5.2 Unfolding
To unfold this integral, we rely on the following lemma.
Lemma 5.4. Every rank-one element of
![]() $W$
has a
$W$
has a
 $\operatorname{GSp}_{6}(\mathbf{Q})$
translate with
$\operatorname{GSp}_{6}(\mathbf{Q})$
translate with
![]() $d=1$
.
$d=1$
.
Proof. Suppose our rank-one element
![]() $v$
is
$v$
is
 $(a,b,c,d)$
. If either
$(a,b,c,d)$
. If either
![]() $a$
or
$a$
or
![]() $d$
is nonzero, we are done. So, suppose
$d$
is nonzero, we are done. So, suppose
 $v=(0,b,c,0)$
. Then
$v=(0,b,c,0)$
. Then
 $(0,b,c,0)n(X)=(0,b,c+b\times X,\operatorname{tr}(c,X)+\operatorname{tr}(b,X^{\sharp }))$
. Since
$(0,b,c,0)n(X)=(0,b,c+b\times X,\operatorname{tr}(c,X)+\operatorname{tr}(b,X^{\sharp }))$
. Since
![]() $v$
is rank one, by Proposition 2.5,
$v$
is rank one, by Proposition 2.5,
 $b^{\sharp }=c^{\sharp }=0$
. From the formula (2.3) for
$b^{\sharp }=c^{\sharp }=0$
. From the formula (2.3) for
![]() $\sharp$
, since
$\sharp$
, since
![]() $B$
is not split, we cannot have both
$B$
is not split, we cannot have both
![]() $c$
purely imaginary and
$c$
purely imaginary and
![]() $c^{\sharp }=0$
, unless
$c^{\sharp }=0$
, unless
![]() $c=0$
. The same for
$c=0$
. The same for
![]() $b$
. Without loss of generality, assume
$b$
. Without loss of generality, assume
![]() $c\neq 0$
. Since
$c\neq 0$
. Since
![]() $c$
is not purely imaginary, there exists
$c$
is not purely imaginary, there exists
 $X\in H_{3}(\mathbf{Q})$
with
$X\in H_{3}(\mathbf{Q})$
with
 $\operatorname{tr}(c,X)\neq 0$
. Hence
$\operatorname{tr}(c,X)\neq 0$
. Hence
 $\unicode[STIX]{x1D706}\operatorname{tr}(c,X)+\unicode[STIX]{x1D706}^{2}\operatorname{tr}(b,X^{\sharp })$
is not zero for some
$\unicode[STIX]{x1D706}\operatorname{tr}(c,X)+\unicode[STIX]{x1D706}^{2}\operatorname{tr}(b,X^{\sharp })$
is not zero for some
![]() $\unicode[STIX]{x1D706}$
in
$\unicode[STIX]{x1D706}$
in
![]() $\mathbf{Q}$
, proving the lemma.◻
$\mathbf{Q}$
, proving the lemma.◻
To do the unfolding, we need to understand the double coset space
 $P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})/\!\operatorname{GSp}_{6}(\mathbf{Q})$
, or equivalently, the
$P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})/\!\operatorname{GSp}_{6}(\mathbf{Q})$
, or equivalently, the
 $\operatorname{GSp}_{6}(\mathbf{Q})$
orbits on the rank-one lines. Recall that
$\operatorname{GSp}_{6}(\mathbf{Q})$
orbits on the rank-one lines. Recall that
![]() $T$
denotes a half-integral symmetric
$T$
denotes a half-integral symmetric
![]() $3\times 3$
matrix that corresponds to the order
$3\times 3$
matrix that corresponds to the order
![]() $B_{0}$
, and set
$B_{0}$
, and set
![]() $A(T)$
to be the rank-one matrix in
$A(T)$
to be the rank-one matrix in
![]() $H_{3}(B)$
from Lemma 3.8. Define
$H_{3}(B)$
from Lemma 3.8. Define
 $f_{{\mathcal{O}}}=(0,0,A(T),0)$
in
$f_{{\mathcal{O}}}=(0,0,A(T),0)$
in
![]() $W$
. By Proposition 2.5,
$W$
. By Proposition 2.5,
![]() $f_{{\mathcal{O}}}$
is rank one. If
$f_{{\mathcal{O}}}$
is rank one. If
![]() $v$
is a rank-one element of
$v$
is a rank-one element of
![]() $W(\mathbf{Q})$
, an orbit
$W(\mathbf{Q})$
, an orbit
 $\mathbf{Q}v\operatorname{GSp}_{6}(\mathbf{Q})$
is said to be negligible if the stabilizer of
$\mathbf{Q}v\operatorname{GSp}_{6}(\mathbf{Q})$
is said to be negligible if the stabilizer of
![]() $\mathbf{Q}v$
in
$\mathbf{Q}v$
in
 $\operatorname{GSp}_{6}(\mathbf{Q})$
contains the unipotent radical of a parabolic subgroup of
$\operatorname{GSp}_{6}(\mathbf{Q})$
contains the unipotent radical of a parabolic subgroup of
![]() $\operatorname{GSp}_{6}$
.
$\operatorname{GSp}_{6}$
.
Proposition 5.5. The line
![]() $\mathbf{Q}f_{{\mathcal{O}}}$
represents the unique open orbit in
$\mathbf{Q}f_{{\mathcal{O}}}$
represents the unique open orbit in
 $P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})/\!\operatorname{GSp}_{6}(\mathbf{Q})$
. There are an infinite number of other orbits, but they are all negligible. The stabilizer of the line
$P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})/\!\operatorname{GSp}_{6}(\mathbf{Q})$
. There are an infinite number of other orbits, but they are all negligible. The stabilizer of the line
![]() $\mathbf{Q}f_{{\mathcal{O}}}$
is the set of elements of
$\mathbf{Q}f_{{\mathcal{O}}}$
is the set of elements of
![]() $\operatorname{GSp}_{6}$
of the form
$\operatorname{GSp}_{6}$
of the form
 $g=(\!\begin{smallmatrix}\unicode[STIX]{x1D706}_{1} & \\ & \unicode[STIX]{x1D706}_{2}\end{smallmatrix}\!)(\!\begin{smallmatrix}1 & U\\ & 1\end{smallmatrix}\!)$
with
$g=(\!\begin{smallmatrix}\unicode[STIX]{x1D706}_{1} & \\ & \unicode[STIX]{x1D706}_{2}\end{smallmatrix}\!)(\!\begin{smallmatrix}1 & U\\ & 1\end{smallmatrix}\!)$
with
![]() $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
in
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}$
in
 $\operatorname{GL}_{1}(\mathbf{Q})$
and
$\operatorname{GL}_{1}(\mathbf{Q})$
and
 $\operatorname{tr}(TU)=0$
.
$\operatorname{tr}(TU)=0$
.
Remark 5.6. This is another spot where defining the group
![]() $\text{G}$
in terms of the Freudenthal construction gives one a serious technical advantage. Here, since
$\text{G}$
in terms of the Freudenthal construction gives one a serious technical advantage. Here, since
 $P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})$
parametrizes the rank-one lines in
$P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})$
parametrizes the rank-one lines in
![]() $W(\mathbf{Q})$
, the use of
$W(\mathbf{Q})$
, the use of
![]() $W$
allows one to see the action of
$W$
allows one to see the action of
 $\operatorname{GSp}_{6}(\mathbf{Q})$
on the coset space
$\operatorname{GSp}_{6}(\mathbf{Q})$
on the coset space
 $P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})$
as a linear action. This linearization makes the double coset computation simple.
$P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})$
as a linear action. This linearization makes the double coset computation simple.
Before giving the proof, define
 $J_{6}=e_{1}\bigwedge f_{1}+e_{2}\bigwedge f_{2}+e_{3}\bigwedge f_{3}$
. Note that if
$J_{6}=e_{1}\bigwedge f_{1}+e_{2}\bigwedge f_{2}+e_{3}\bigwedge f_{3}$
. Note that if
 $a_{1},a_{2},a_{3}$
in
$a_{1},a_{2},a_{3}$
in
![]() $B$
are purely imaginary, and
$B$
are purely imaginary, and
 $c_{1},c_{2},c_{3}$
are in
$c_{1},c_{2},c_{3}$
are in
![]() $\mathbf{Q}$
, then
$\mathbf{Q}$
, then
 $$\begin{eqnarray}(a_{1}f_{1}+a_{2}f_{2}+a_{3}f_{3})\wedge J_{6}+c_{1}e_{1}\wedge f_{2}\wedge f_{3}+c_{2}f_{1}\wedge e_{2}\wedge f_{3}+c_{3}f_{1}\wedge f_{2}\wedge e_{3}\end{eqnarray}$$
$$\begin{eqnarray}(a_{1}f_{1}+a_{2}f_{2}+a_{3}f_{3})\wedge J_{6}+c_{1}e_{1}\wedge f_{2}\wedge f_{3}+c_{2}f_{1}\wedge e_{2}\wedge f_{3}+c_{3}f_{1}\wedge f_{2}\wedge e_{3}\end{eqnarray}$$
is the element
 $$\begin{eqnarray}\left(0,0,\left(\begin{array}{@{}ccc@{}}c_{1} & a_{3} & -a_{2}\\ -a_{3} & c_{2} & a_{1}\\ a_{2} & -a_{1} & c_{3}\end{array}\right),0\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(0,0,\left(\begin{array}{@{}ccc@{}}c_{1} & a_{3} & -a_{2}\\ -a_{3} & c_{2} & a_{1}\\ a_{2} & -a_{1} & c_{3}\end{array}\right),0\right)\end{eqnarray}$$
of
![]() $W$
.
$W$
.
Proof of Proposition 5.5.
Suppose we are given a rank-one element
 $v=(a,b,c,d)$
of
$v=(a,b,c,d)$
of
![]() $W(\mathbf{Q})$
. We will first use the action of
$W(\mathbf{Q})$
. We will first use the action of
 $\operatorname{GSp}_{6}(\mathbf{Q})$
to put it into a standard form. By Lemma 5.4, we may assume
$\operatorname{GSp}_{6}(\mathbf{Q})$
to put it into a standard form. By Lemma 5.4, we may assume
![]() $d=1$
. Then our element is of the form
$d=1$
. Then our element is of the form
 $(N(c),c^{\#},c,1)$
. Now use the transformations
$(N(c),c^{\#},c,1)$
. Now use the transformations
![]() $\overline{n}(Y)$
to make
$\overline{n}(Y)$
to make
![]() $c$
purely imaginary.
$c$
purely imaginary.
Denote by
![]() $M_{P,6}$
the Levi subgroup of the Siegel parabolic on
$M_{P,6}$
the Levi subgroup of the Siegel parabolic on
![]() $\operatorname{GSp}_{6}$
, i.e., the elements of
$\operatorname{GSp}_{6}$
, i.e., the elements of
![]() $\operatorname{GSp}_{6}$
of the form
$\operatorname{GSp}_{6}$
of the form
![]() $(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)$
. By formula (5.5),
$(\!\begin{smallmatrix}m & \\ & n\end{smallmatrix}\!)$
. By formula (5.5),
![]() $M_{P,6}$
acts on the space of such
$M_{P,6}$
acts on the space of such
![]() $c$
values as
$c$
values as
 $B^{\operatorname{tr}=0}\otimes _{\mathbf{Q}}\,\text{span}\{f_{1},f_{2},f_{3}\}$
. That is,
$B^{\operatorname{tr}=0}\otimes _{\mathbf{Q}}\,\text{span}\{f_{1},f_{2},f_{3}\}$
. That is,
![]() $M_{P,6}$
acts on these
$M_{P,6}$
acts on these
![]() $c$
values via its usual action on
$c$
values via its usual action on
 $\text{span}\{f_{1},f_{2},f_{3}\}\subseteq W_{6}$
, linearly extended to
$\text{span}\{f_{1},f_{2},f_{3}\}\subseteq W_{6}$
, linearly extended to
 $B^{\operatorname{tr}=0}\otimes _{\mathbf{Q}}\,\text{span}\{f_{1},f_{2},f_{3}\}$
. Pick a basis
$B^{\operatorname{tr}=0}\otimes _{\mathbf{Q}}\,\text{span}\{f_{1},f_{2},f_{3}\}$
. Pick a basis
![]() $i,j,k$
of
$i,j,k$
of
![]() $B^{\operatorname{tr}=0}$
, and suppose
$B^{\operatorname{tr}=0}$
, and suppose
 $c=i\otimes v_{1}+j\otimes v_{2}+k\otimes v_{3}$
. We have four different cases, depending on whether
$c=i\otimes v_{1}+j\otimes v_{2}+k\otimes v_{3}$
. We have four different cases, depending on whether
 $\text{dim}\,\text{span}\{v_{1},v_{2},v_{3}\}$
is 0, 1, 2 or 3. (Note that this dimension is not a
$\text{dim}\,\text{span}\{v_{1},v_{2},v_{3}\}$
is 0, 1, 2 or 3. (Note that this dimension is not a
![]() $\operatorname{GSp}_{6}$
invariant of the orbit, just an
$\operatorname{GSp}_{6}$
invariant of the orbit, just an
![]() $M_{P,6}$
invariant.) If the dimension is 0, i.e,
$M_{P,6}$
invariant.) If the dimension is 0, i.e,
![]() $c=0$
, then we are in the orbit of
$c=0$
, then we are in the orbit of
![]() $f$
, which is negligible. There are an infinite number of orbits with
$f$
, which is negligible. There are an infinite number of orbits with
 $\text{dim}\,\text{span}\{v_{1},v_{2},v_{3}\}=1$
. Given such an orbit, we can use
$\text{dim}\,\text{span}\{v_{1},v_{2},v_{3}\}=1$
. Given such an orbit, we can use
![]() $M_{P,6}$
to move
$M_{P,6}$
to move
![]() $c$
to
$c$
to
![]() $h\otimes f_{1}$
with
$h\otimes f_{1}$
with
 $h\in B^{\operatorname{tr}=0}$
. Then this orbit is stabilized by
$h\in B^{\operatorname{tr}=0}$
. Then this orbit is stabilized by
![]() $U_{Q}(f_{1})$
, the unipotent radical of the parabolic subgroup of
$U_{Q}(f_{1})$
, the unipotent radical of the parabolic subgroup of
![]() $\operatorname{GSp}_{6}$
stabilizing the line
$\operatorname{GSp}_{6}$
stabilizing the line
 $\mathbf{Q}f_{1}\subseteq W_{6}$
. Thus, this orbit is also negligible. We will show that there is a unique orbit with
$\mathbf{Q}f_{1}\subseteq W_{6}$
. Thus, this orbit is also negligible. We will show that there is a unique orbit with
 $\dim =3$
, and that this orbit is represented by
$\dim =3$
, and that this orbit is represented by
![]() $f_{{\mathcal{O}}}$
. Furthermore, we will see that the orbit corresponding to
$f_{{\mathcal{O}}}$
. Furthermore, we will see that the orbit corresponding to
 $\dim =2$
is the same as the
$\dim =2$
is the same as the
 $\dim =3$
orbit.
$\dim =3$
orbit.
First, for
 $\dim =3$
, use
$\dim =3$
, use
![]() $M_{P,6}$
to move
$M_{P,6}$
to move
![]() $c$
to
$c$
to
 $i\otimes f_{1}+j\otimes f_{2}+k\otimes f_{3}$
, proving that there is one such orbit.
$i\otimes f_{1}+j\otimes f_{2}+k\otimes f_{3}$
, proving that there is one such orbit.
Now we consider a
 $\dim =2$
orbit. Here we have
$\dim =2$
orbit. Here we have
 $c=i\otimes v_{1}+j\otimes v_{2}+k\otimes v_{3}$
with one of the
$c=i\otimes v_{1}+j\otimes v_{2}+k\otimes v_{3}$
with one of the
![]() $v_{i}$
in the span of the other two. Thus we may use
$v_{i}$
in the span of the other two. Thus we may use
![]() $M_{P,6}$
to move this orbit to one with
$M_{P,6}$
to move this orbit to one with
 $c=h_{1}\otimes f_{1}+h_{2}\otimes f_{2}$
, with
$c=h_{1}\otimes f_{1}+h_{2}\otimes f_{2}$
, with
![]() $h_{1},h_{2}$
in
$h_{1},h_{2}$
in
![]() $B^{\operatorname{tr}=0}$
. If
$B^{\operatorname{tr}=0}$
. If
 $\dim \text{span}\{h_{1},h_{2}\}=1$
, then we are really in the
$\dim \text{span}\{h_{1},h_{2}\}=1$
, then we are really in the
 $\dim =1$
case. Thus we have that
$\dim =1$
case. Thus we have that
![]() $h_{1},h_{2}$
are linearly independent.
$h_{1},h_{2}$
are linearly independent.
Now
 $$\begin{eqnarray}c=\left(\begin{array}{@{}ccc@{}}0 & 0 & -h_{2}\\ 0 & 0 & h_{1}\\ h_{2} & -h_{1} & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}c=\left(\begin{array}{@{}ccc@{}}0 & 0 & -h_{2}\\ 0 & 0 & h_{1}\\ h_{2} & -h_{1} & 0\end{array}\right),\end{eqnarray}$$
from which we obtain
 $$\begin{eqnarray}c^{\sharp }=\left(\begin{array}{@{}ccc@{}}-n(h_{1}) & h_{2}h_{1} & 0\\ h_{1}h_{2} & -n(h_{2}) & 0\\ 0 & 0 & 0\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}c^{\sharp }=\left(\begin{array}{@{}ccc@{}}-n(h_{1}) & h_{2}h_{1} & 0\\ h_{1}h_{2} & -n(h_{2}) & 0\\ 0 & 0 & 0\end{array}\right)\end{eqnarray}$$
and
 $N(c)=0$
. Hence we have that
$N(c)=0$
. Hence we have that
 $v=(N(c),c^{\#},c,1)$
is
$v=(N(c),c^{\#},c,1)$
is
 $$\begin{eqnarray}-n(h_{1})e_{1}^{\ast }\wedge f_{1}-n(h_{2})e_{2}^{\ast }\wedge f_{2}+h_{1}h_{2}e_{2}^{\ast }\wedge f_{1}+h_{2}h_{1}e_{1}^{\ast }\wedge f_{2}+(h_{1}f_{1}+h_{2}f_{2})\wedge J_{6}+f_{1}\wedge f_{2}\wedge f_{3}.\end{eqnarray}$$
$$\begin{eqnarray}-n(h_{1})e_{1}^{\ast }\wedge f_{1}-n(h_{2})e_{2}^{\ast }\wedge f_{2}+h_{1}h_{2}e_{2}^{\ast }\wedge f_{1}+h_{2}h_{1}e_{1}^{\ast }\wedge f_{2}+(h_{1}f_{1}+h_{2}f_{2})\wedge J_{6}+f_{1}\wedge f_{2}\wedge f_{3}.\end{eqnarray}$$
Now apply to
![]() $v$
the element of
$v$
the element of
![]() $\operatorname{GSp}_{6}$
that takes
$\operatorname{GSp}_{6}$
that takes
 $e_{3}\mapsto f_{3}$
,
$e_{3}\mapsto f_{3}$
,
 $f_{3}\mapsto -e_{3}$
and is the identity on
$f_{3}\mapsto -e_{3}$
and is the identity on
 $e_{1},e_{2},f_{1},f_{2}$
. One obtains the element
$e_{1},e_{2},f_{1},f_{2}$
. One obtains the element
 $v^{\prime }=(0,0,h,0)$
, with
$v^{\prime }=(0,0,h,0)$
, with
 $$\begin{eqnarray}h=\left(\begin{array}{@{}ccc@{}}-n(h_{2}) & -h_{2}h_{1} & -h_{2}\\ -h_{1}h_{2} & -n(h_{1}) & h_{1}\\ h_{2} & -h_{1} & -1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}h=\left(\begin{array}{@{}ccc@{}}-n(h_{2}) & -h_{2}h_{1} & -h_{2}\\ -h_{1}h_{2} & -n(h_{1}) & h_{1}\\ h_{2} & -h_{1} & -1\end{array}\right).\end{eqnarray}$$
Since
![]() $B$
is not split,
$B$
is not split,
![]() $h_{1}h_{2}$
is not in the span of
$h_{1}h_{2}$
is not in the span of
 $1,h_{1},h_{2}$
. Take
$1,h_{1},h_{2}$
. Take
![]() $h_{3}$
in
$h_{3}$
in
![]() $B^{\operatorname{tr}=0}$
with
$B^{\operatorname{tr}=0}$
with
 $h_{1}h_{2}-h_{3}$
in
$h_{1}h_{2}-h_{3}$
in
![]() $\mathbf{Q}$
. Then
$\mathbf{Q}$
. Then
 $\operatorname{Im}(h)=(h_{1}f_{1}+h_{2}f_{2}+h_{3}f_{3})\bigwedge J_{6}$
. Since
$\operatorname{Im}(h)=(h_{1}f_{1}+h_{2}f_{2}+h_{3}f_{3})\bigwedge J_{6}$
. Since
 $$\begin{eqnarray}h_{1}\otimes f_{1}+h_{2}\otimes f_{2}+h_{3}\otimes f_{3}=i\otimes v_{1}+j\otimes v_{2}+k\otimes v_{3}\end{eqnarray}$$
$$\begin{eqnarray}h_{1}\otimes f_{1}+h_{2}\otimes f_{2}+h_{3}\otimes f_{3}=i\otimes v_{1}+j\otimes v_{2}+k\otimes v_{3}\end{eqnarray}$$
for some
 $v_{1},v_{2},v_{3}$
spanning
$v_{1},v_{2},v_{3}$
spanning
 $\langle f_{1},f_{2},f_{3}\rangle$
, the
$\langle f_{1},f_{2},f_{3}\rangle$
, the
 $\dim =2$
orbit is the same as the
$\dim =2$
orbit is the same as the
 $\dim =3$
orbit.
$\dim =3$
orbit.
The element
![]() $f_{{\mathcal{O}}}$
clearly represents the
$f_{{\mathcal{O}}}$
clearly represents the
 $\dim =3$
orbit. To compute the stabilizer, note that by (5.5) we immediately see that if
$\dim =3$
orbit. To compute the stabilizer, note that by (5.5) we immediately see that if
 $f_{{\mathcal{O}}}g=f_{{\mathcal{O}}}$
, then
$f_{{\mathcal{O}}}g=f_{{\mathcal{O}}}$
, then
 $f_{1}g=f_{1},f_{2}g=f_{2},f_{3}g=f_{3}$
. Hence an element of the stabilizer must be of the form
$f_{1}g=f_{1},f_{2}g=f_{2},f_{3}g=f_{3}$
. Hence an element of the stabilizer must be of the form
 $g=(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & 1\end{smallmatrix}\!)(\!\begin{smallmatrix}1 & U\\ & 1\end{smallmatrix}\!)$
. Applying this element to
$g=(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & 1\end{smallmatrix}\!)(\!\begin{smallmatrix}1 & U\\ & 1\end{smallmatrix}\!)$
. Applying this element to
![]() $f_{{\mathcal{O}}}$
, we find it stabilizes
$f_{{\mathcal{O}}}$
, we find it stabilizes
![]() $f_{{\mathcal{O}}}$
if and only if
$f_{{\mathcal{O}}}$
if and only if
 $\operatorname{tr}(TU)=0$
, completing the proof.◻
$\operatorname{tr}(TU)=0$
, completing the proof.◻
Recall the partially normalized Eisenstein series
 $E^{\unicode[STIX]{x1D6F7}}(g,s)$
from above, and set
$E^{\unicode[STIX]{x1D6F7}}(g,s)$
from above, and set
 $$\begin{eqnarray}I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{\operatorname{GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)E^{\unicode[STIX]{x1D6F7}}(g,s)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{\operatorname{GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)E^{\unicode[STIX]{x1D6F7}}(g,s)\,dg.\end{eqnarray}$$
We will consider the integral
 $I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
for now, and add back in the other normalizing factors later.
$I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
for now, and add back in the other normalizing factors later.
Write
![]() $U_{P}$
for the unipotent radical of the Siegel parabolic of
$U_{P}$
for the unipotent radical of the Siegel parabolic of
![]() $\operatorname{GSp}_{6}$
. The group
$\operatorname{GSp}_{6}$
. The group
![]() $U_{P}$
consists of the matrices
$U_{P}$
consists of the matrices
![]() $(\!\begin{smallmatrix}1 & u\\ & 1\end{smallmatrix}\!)$
with
$(\!\begin{smallmatrix}1 & u\\ & 1\end{smallmatrix}\!)$
with
![]() $u=^{t}u$
. Define
$u=^{t}u$
. Define
 $U_{0}\subseteq U_{P}$
to be the elements with
$U_{0}\subseteq U_{P}$
to be the elements with
 $\operatorname{tr}(Tu)=0$
. Write
$\operatorname{tr}(Tu)=0$
. Write
 $\unicode[STIX]{x1D713}:\mathbf{Q}\backslash \mathbf{A}\rightarrow \mathbf{C}^{\times }$
for the usual additive character of conductor 1 satisfying
$\unicode[STIX]{x1D713}:\mathbf{Q}\backslash \mathbf{A}\rightarrow \mathbf{C}^{\times }$
for the usual additive character of conductor 1 satisfying
 $\unicode[STIX]{x1D713}_{\infty }(x)=e^{2\unicode[STIX]{x1D70B}ix}$
for
$\unicode[STIX]{x1D713}_{\infty }(x)=e^{2\unicode[STIX]{x1D70B}ix}$
for
![]() $x\in \mathbf{R}$
. Define
$x\in \mathbf{R}$
. Define
 $\unicode[STIX]{x1D712}:U_{P}(\mathbf{Q})\backslash U_{P}(\mathbf{A})\rightarrow \mathbf{C}^{\times }$
via
$\unicode[STIX]{x1D712}:U_{P}(\mathbf{Q})\backslash U_{P}(\mathbf{A})\rightarrow \mathbf{C}^{\times }$
via
 $\unicode[STIX]{x1D712}((\!\begin{smallmatrix}1 & h\\ & 1\end{smallmatrix}\!))=\unicode[STIX]{x1D713}(\operatorname{tr}(Th))$
, and set
$\unicode[STIX]{x1D712}((\!\begin{smallmatrix}1 & h\\ & 1\end{smallmatrix}\!))=\unicode[STIX]{x1D713}(\operatorname{tr}(Th))$
, and set
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)=\int _{U_{P}(\mathbf{Q})\backslash U_{P}(\mathbf{A})}\unicode[STIX]{x1D712}^{-1}(u)\unicode[STIX]{x1D719}(ug)\,du.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)=\int _{U_{P}(\mathbf{Q})\backslash U_{P}(\mathbf{A})}\unicode[STIX]{x1D712}^{-1}(u)\unicode[STIX]{x1D719}(ug)\,du.\end{eqnarray}$$
Theorem 5.7. The global integrals
 $I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s),I_{2r}^{\ast }(\unicode[STIX]{x1D719},s)$
converge absolutely for all
$I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s),I_{2r}^{\ast }(\unicode[STIX]{x1D719},s)$
converge absolutely for all
![]() $s$
for which the Eisenstein series
$s$
for which the Eisenstein series
 $E^{\unicode[STIX]{x1D6F7}}(g,s)$
, respectively,
$E^{\unicode[STIX]{x1D6F7}}(g,s)$
, respectively,
 $E_{2r}^{\ast }(g,s)$
is finite, and thus define a meromorphic function of
$E_{2r}^{\ast }(g,s)$
is finite, and thus define a meromorphic function of
![]() $s$
. For
$s$
. For
![]() $\text{Re}(s)$
sufficiently large, the integral
$\text{Re}(s)$
sufficiently large, the integral
 $I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
unfolds as
$I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
unfolds as
 $$\begin{eqnarray}\displaystyle I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s) & = & \displaystyle \int _{U_{0}(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)|\unicode[STIX]{x1D708}(g)|^{s}\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}g)\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{P}(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)|\unicode[STIX]{x1D708}(g)|^{s}\biggl(\int _{U_{0}(\mathbf{A})\backslash U_{P}(\mathbf{A})}\unicode[STIX]{x1D712}(u)\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}ug)\,du\biggr)\,dg.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s) & = & \displaystyle \int _{U_{0}(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)|\unicode[STIX]{x1D708}(g)|^{s}\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}g)\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{P}(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)|\unicode[STIX]{x1D708}(g)|^{s}\biggl(\int _{U_{0}(\mathbf{A})\backslash U_{P}(\mathbf{A})}\unicode[STIX]{x1D712}(u)\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}ug)\,du\biggr)\,dg.\nonumber\end{eqnarray}$$
Proof. The Eisenstein series
 $E^{\unicode[STIX]{x1D6F7}}(g,s)$
is a function of moderate growth wherever it is finite. Since the cusp form
$E^{\unicode[STIX]{x1D6F7}}(g,s)$
is a function of moderate growth wherever it is finite. Since the cusp form
![]() $\unicode[STIX]{x1D719}$
decreases rapidly on Siegel sets, the integral
$\unicode[STIX]{x1D719}$
decreases rapidly on Siegel sets, the integral
 $I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
converges absolutely for all
$I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
converges absolutely for all
![]() $s$
for which the Eisenstein series is finite.
$s$
for which the Eisenstein series is finite.
Suppose now
 $\text{Re}(s)\gg 0$
, and denote by
$\text{Re}(s)\gg 0$
, and denote by
![]() ${\mathcal{F}}$
a fundamental domain for
${\mathcal{F}}$
a fundamental domain for
 $\operatorname{GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \operatorname{GSp}_{6}(\mathbf{A})$
. Similar to the above, but easier,
$\operatorname{GSp}_{6}(\mathbf{Q})Z(\mathbf{A})\backslash \operatorname{GSp}_{6}(\mathbf{A})$
. Similar to the above, but easier,
 $\sum _{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})}|f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g,s)|$
converges to a function of moderate growth since
$\sum _{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})}|f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g,s)|$
converges to a function of moderate growth since
 $\text{Re}(s)\gg 0$
. Then again since
$\text{Re}(s)\gg 0$
. Then again since
![]() $\unicode[STIX]{x1D719}$
decreases rapidly on Siegel sets, the sum
$\unicode[STIX]{x1D719}$
decreases rapidly on Siegel sets, the sum
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})}\int _{{\mathcal{F}}}|f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g,s)|\,|\unicode[STIX]{x1D719}(g)|\,dg\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})}\int _{{\mathcal{F}}}|f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g,s)|\,|\unicode[STIX]{x1D719}(g)|\,dg\end{eqnarray}$$
is finite. Hence even though there are an infinite number of
 $\operatorname{GSp}_{6}(\mathbf{Q})$
orbits on
$\operatorname{GSp}_{6}(\mathbf{Q})$
orbits on
 $P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})$
, we may analyze them, and check the vanishing of the associated integrals, one by one.
$P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})$
, we may analyze them, and check the vanishing of the associated integrals, one by one.
By Proposition 5.5, we have
 $$\begin{eqnarray}I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{\operatorname{GL}_{1}(\mathbf{Q})U_{0}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}_{0}g,s)\,dg\end{eqnarray}$$
$$\begin{eqnarray}I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{\operatorname{GL}_{1}(\mathbf{Q})U_{0}(\mathbf{Q})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}(g)f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}_{0}g,s)\,dg\end{eqnarray}$$
where the
 $\operatorname{GL}_{1}(\mathbf{Q})$
is the set of elements of
$\operatorname{GL}_{1}(\mathbf{Q})$
is the set of elements of
 $\operatorname{GSp}_{6}(\mathbf{Q})$
of the form
$\operatorname{GSp}_{6}(\mathbf{Q})$
of the form
![]() $(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & 1\end{smallmatrix}\!)$
, with
$(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & 1\end{smallmatrix}\!)$
, with
![]() $\unicode[STIX]{x1D706}\in \mathbf{Q}^{\times }$
, and
$\unicode[STIX]{x1D706}\in \mathbf{Q}^{\times }$
, and
 $\unicode[STIX]{x1D6FE}_{0}\in \text{G}(\mathbf{Q})$
satisfies
$\unicode[STIX]{x1D6FE}_{0}\in \text{G}(\mathbf{Q})$
satisfies
 $(0,0,0,1)\unicode[STIX]{x1D6FE}_{0}=f_{{\mathcal{O}}}$
. Indeed, this is the term from the open orbit, and the negligible orbits contribute zero by the cuspidality of
$(0,0,0,1)\unicode[STIX]{x1D6FE}_{0}=f_{{\mathcal{O}}}$
. Indeed, this is the term from the open orbit, and the negligible orbits contribute zero by the cuspidality of
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
Now we integrate
![]() $\unicode[STIX]{x1D719}$
over
$\unicode[STIX]{x1D719}$
over
 $U_{0}(\mathbf{Q})\backslash U_{0}(\mathbf{A})$
and Fourier expand:
$U_{0}(\mathbf{Q})\backslash U_{0}(\mathbf{A})$
and Fourier expand:
 $$\begin{eqnarray}\int _{U_{0}(\mathbf{Q})\backslash U_{0}(\mathbf{A})}\unicode[STIX]{x1D719}(ug)\,du=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{1}(\mathbf{Q})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FE}g).\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{0}(\mathbf{Q})\backslash U_{0}(\mathbf{A})}\unicode[STIX]{x1D719}(ug)\,du=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{1}(\mathbf{Q})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D6FE}g).\end{eqnarray}$$
Placing this Fourier expansion into (5.7) we get
 $$\begin{eqnarray}I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{U_{0}(\mathbf{A})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}_{0}g,s)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{U_{0}(\mathbf{A})Z(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}_{0}g,s)\,dg.\end{eqnarray}$$
Integrating
 $$\begin{eqnarray}\int _{U_{0}(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}|\unicode[STIX]{x1D708}(g)|^{s}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}g)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{0}(\mathbf{A})\backslash \!\operatorname{GSp}_{6}(\mathbf{A})}|\unicode[STIX]{x1D708}(g)|^{s}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}g)\,dg\end{eqnarray}$$
over
![]() $Z(\mathbf{A})$
one obtains (5.8), giving the theorem.◻
$Z(\mathbf{A})$
one obtains (5.8), giving the theorem.◻
Remark 5.8. In Theorem 5.7, we could have chosen to unfold the global integral
 $I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
to any Fourier coefficient
$I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)$
to any Fourier coefficient
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}^{\prime }}(g)$
, where
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}^{\prime }}(g)$
, where
 $\unicode[STIX]{x1D712}^{\prime }((\!\begin{smallmatrix}1 & h\\ & 1\end{smallmatrix}\!))=\unicode[STIX]{x1D713}(\operatorname{tr}(T^{\prime }h))$
and the quaternion algebra associated to
$\unicode[STIX]{x1D712}^{\prime }((\!\begin{smallmatrix}1 & h\\ & 1\end{smallmatrix}\!))=\unicode[STIX]{x1D713}(\operatorname{tr}(T^{\prime }h))$
and the quaternion algebra associated to
![]() $T^{\prime }$
is
$T^{\prime }$
is
![]() $B$
. Using
$B$
. Using
![]() $T^{\prime }$
instead of
$T^{\prime }$
instead of
![]() $T$
would have no effect on the results or proofs in § 5.2. However, using
$T$
would have no effect on the results or proofs in § 5.2. However, using
![]() $T$
that corresponds to the maximal order
$T$
that corresponds to the maximal order
![]() $B_{0}$
did make a difference in Corollary 4.2, and will also make a difference in Proposition 6.1 below.
$B_{0}$
did make a difference in Corollary 4.2, and will also make a difference in Proposition 6.1 below.
6 Evaluation of the integral
In this section we relate the unfolded Rankin–Selberg integral to the Spin
![]() $L$
-function.
$L$
-function.
6.1 The finite places
Our first task is to compute the unipotent integral
 $\int _{U_{0}\backslash U_{P}}\unicode[STIX]{x1D712}(u)\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}ug)\,du$
. For an element
$\int _{U_{0}\backslash U_{P}}\unicode[STIX]{x1D712}(u)\unicode[STIX]{x1D6F7}(f_{{\mathcal{O}}}ug)\,du$
. For an element
 $m\in \operatorname{GL}_{3}$
, and an element
$m\in \operatorname{GL}_{3}$
, and an element
 $\unicode[STIX]{x1D706}\in \operatorname{GL}_{1}$
, we set
$\unicode[STIX]{x1D706}\in \operatorname{GL}_{1}$
, we set

an element of
![]() $\operatorname{GSp}_{6}$
. For
$\operatorname{GSp}_{6}$
. For
 $(\unicode[STIX]{x1D706},m)\in \operatorname{GL}_{1}(\mathbf{A}_{f})\times \operatorname{GL}_{3}(\mathbf{A}_{f})$
, we define
$(\unicode[STIX]{x1D706},m)\in \operatorname{GL}_{1}(\mathbf{A}_{f})\times \operatorname{GL}_{3}(\mathbf{A}_{f})$
, we define
 $$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m):=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if}~\unicode[STIX]{x1D706}\in \widehat{\mathbf{Z}},m\in M_{3}(\widehat{\mathbf{Z}}),\text{and}~m^{-1}Tc(m)\in M_{3}(\widehat{\mathbf{Z}}),\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m):=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if}~\unicode[STIX]{x1D706}\in \widehat{\mathbf{Z}},m\in M_{3}(\widehat{\mathbf{Z}}),\text{and}~m^{-1}Tc(m)\in M_{3}(\widehat{\mathbf{Z}}),\\ 0\quad & \text{otherwise}.\end{array}\right.\end{eqnarray}$$
Proposition 6.1. The integral
 $$\begin{eqnarray}\int _{U_{0}(\mathbf{A}_{f})\backslash U_{P}(\mathbf{A}_{f})}\unicode[STIX]{x1D712}(u)\unicode[STIX]{x1D6F7}_{f}(f_{{\mathcal{O}}}u(\unicode[STIX]{x1D706},m))\,du=|\unicode[STIX]{x1D706}|_{f}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m).\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{0}(\mathbf{A}_{f})\backslash U_{P}(\mathbf{A}_{f})}\unicode[STIX]{x1D712}(u)\unicode[STIX]{x1D6F7}_{f}(f_{{\mathcal{O}}}u(\unicode[STIX]{x1D706},m))\,du=|\unicode[STIX]{x1D706}|_{f}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m).\end{eqnarray}$$
Proof. Recall the lattice
![]() $J_{0}$
in
$J_{0}$
in
![]() $H_{3}(B)$
defined in (5.4), and set
$H_{3}(B)$
defined in (5.4), and set
 $J_{0}(\widehat{\mathbf{Z}})=J_{0}\otimes _{\mathbf{Z}}\widehat{\mathbf{Z}}$
. Suppose
$J_{0}(\widehat{\mathbf{Z}})=J_{0}\otimes _{\mathbf{Z}}\widehat{\mathbf{Z}}$
. Suppose
 $h=(\unicode[STIX]{x1D706},m)$
. One computes
$h=(\unicode[STIX]{x1D706},m)$
. One computes
 $$\begin{eqnarray}f_{{\mathcal{O}}}n(u)h=\biggl(0,0,m^{-1}A(T)c(m),\frac{\operatorname{tr}(Tu)}{\unicode[STIX]{x1D706}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}f_{{\mathcal{O}}}n(u)h=\biggl(0,0,m^{-1}A(T)c(m),\frac{\operatorname{tr}(Tu)}{\unicode[STIX]{x1D706}}\biggr).\end{eqnarray}$$
Hence for the integral (6.1) to be nonzero, one needs
 $m^{-1}A(T)c(m)$
to be in
$m^{-1}A(T)c(m)$
to be in
![]() $J_{0}(\widehat{\mathbf{Z}})$
and the integral
$J_{0}(\widehat{\mathbf{Z}})$
and the integral
 $$\begin{eqnarray}\int _{U_{0}(\mathbf{A}_{f})\backslash U_{P}(\mathbf{A}_{f})}\unicode[STIX]{x1D713}(\operatorname{tr}(Tu))\operatorname{char}\biggl(\frac{\operatorname{tr}(Tu)}{\unicode[STIX]{x1D706}}\in \widehat{\mathbf{Z}}\biggr)\,du\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{0}(\mathbf{A}_{f})\backslash U_{P}(\mathbf{A}_{f})}\unicode[STIX]{x1D713}(\operatorname{tr}(Tu))\operatorname{char}\biggl(\frac{\operatorname{tr}(Tu)}{\unicode[STIX]{x1D706}}\in \widehat{\mathbf{Z}}\biggr)\,du\end{eqnarray}$$
to be nonzero. By Lemma 3.8,
 $m^{-1}A(T)c(m)$
is in
$m^{-1}A(T)c(m)$
is in
![]() $J_{0}(\widehat{\mathbf{Z}})$
if and only if
$J_{0}(\widehat{\mathbf{Z}})$
if and only if
 $m\in M_{3}(\widehat{\mathbf{Z}})$
and
$m\in M_{3}(\widehat{\mathbf{Z}})$
and
 $m^{-1}Tc(m)\in M_{3}(\widehat{\mathbf{Z}})$
. The integral (6.3) is zero when
$m^{-1}Tc(m)\in M_{3}(\widehat{\mathbf{Z}})$
. The integral (6.3) is zero when
![]() $\unicode[STIX]{x1D706}\notin \widehat{\mathbf{Z}}$
, and is
$\unicode[STIX]{x1D706}\notin \widehat{\mathbf{Z}}$
, and is
![]() $|\unicode[STIX]{x1D706}|_{f}$
when
$|\unicode[STIX]{x1D706}|_{f}$
when
![]() $\unicode[STIX]{x1D706}\in \widehat{\mathbf{Z}}$
. The proposition follows.◻
$\unicode[STIX]{x1D706}\in \widehat{\mathbf{Z}}$
. The proposition follows.◻
The global integral we must compute is
 $$\begin{eqnarray}\displaystyle I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s) & = & \displaystyle \int _{U_{0}(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}|\unicode[STIX]{x1D708}(g_{\infty })|_{\infty }^{s}\unicode[STIX]{x1D6F7}_{\infty }(f_{{\mathcal{O}}}g_{\infty })\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{U_{0}(\mathbf{A}_{f})\backslash \!\operatorname{GSp}_{6}(\mathbf{A}_{f})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{f}g_{\infty })|\unicode[STIX]{x1D708}(g_{f})|_{f}^{s}\unicode[STIX]{x1D6F7}_{f}(f_{{\mathcal{O}}}g_{f})\,dg_{f}\biggr)\,dg_{\infty }\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{0}(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}|\unicode[STIX]{x1D708}(g_{\infty })|_{\infty }^{s}\unicode[STIX]{x1D6F7}_{\infty }(f_{{\mathcal{O}}}g_{\infty })I_{f}(\unicode[STIX]{x1D719},s,g_{\infty })\,dg_{\infty }\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s) & = & \displaystyle \int _{U_{0}(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}|\unicode[STIX]{x1D708}(g_{\infty })|_{\infty }^{s}\unicode[STIX]{x1D6F7}_{\infty }(f_{{\mathcal{O}}}g_{\infty })\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{U_{0}(\mathbf{A}_{f})\backslash \!\operatorname{GSp}_{6}(\mathbf{A}_{f})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{f}g_{\infty })|\unicode[STIX]{x1D708}(g_{f})|_{f}^{s}\unicode[STIX]{x1D6F7}_{f}(f_{{\mathcal{O}}}g_{f})\,dg_{f}\biggr)\,dg_{\infty }\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{0}(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}|\unicode[STIX]{x1D708}(g_{\infty })|_{\infty }^{s}\unicode[STIX]{x1D6F7}_{\infty }(f_{{\mathcal{O}}}g_{\infty })I_{f}(\unicode[STIX]{x1D719},s,g_{\infty })\,dg_{\infty }\nonumber\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle I_{f}(\unicode[STIX]{x1D719},s,g_{\infty }) & = & \displaystyle \int _{U_{0}(\mathbf{A}_{f})\backslash \!\operatorname{GSp}_{6}(\mathbf{A}_{f})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{f}g_{\infty })|\unicode[STIX]{x1D708}(g_{f})|_{f}^{s}\unicode[STIX]{x1D6F7}_{f}(f_{{\mathcal{O}}}g_{f})\,dg_{f}\nonumber\\ \displaystyle & = & \displaystyle \int _{(\operatorname{GL}_{1}\times \operatorname{GL}_{3})(\mathbf{A}_{f})}\unicode[STIX]{x1D6FF}_{P}^{-1}(h)|\text{det}(m)|_{f}^{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D70B}(h)g_{\infty })|\unicode[STIX]{x1D708}(h)|_{f}^{s+1}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m)\,dh.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{f}(\unicode[STIX]{x1D719},s,g_{\infty }) & = & \displaystyle \int _{U_{0}(\mathbf{A}_{f})\backslash \!\operatorname{GSp}_{6}(\mathbf{A}_{f})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{f}g_{\infty })|\unicode[STIX]{x1D708}(g_{f})|_{f}^{s}\unicode[STIX]{x1D6F7}_{f}(f_{{\mathcal{O}}}g_{f})\,dg_{f}\nonumber\\ \displaystyle & = & \displaystyle \int _{(\operatorname{GL}_{1}\times \operatorname{GL}_{3})(\mathbf{A}_{f})}\unicode[STIX]{x1D6FF}_{P}^{-1}(h)|\text{det}(m)|_{f}^{-1}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D70B}(h)g_{\infty })|\unicode[STIX]{x1D708}(h)|_{f}^{s+1}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m)\,dh.\end{eqnarray}$$
Here
 $h=(\unicode[STIX]{x1D706},m)$
,
$h=(\unicode[STIX]{x1D706},m)$
,
![]() $\unicode[STIX]{x1D6FF}_{P}$
denotes the modulus character of the Siegel parabolic in
$\unicode[STIX]{x1D6FF}_{P}$
denotes the modulus character of the Siegel parabolic in
![]() $\operatorname{GSp}_{6}$
, and we have applied Proposition 6.1, the Iwasawa decomposition, and the fact that
$\operatorname{GSp}_{6}$
, and we have applied Proposition 6.1, the Iwasawa decomposition, and the fact that
 $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D708}(h)\det (m)^{-1}$
.
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D708}(h)\det (m)^{-1}$
.
Translating between the classical and adelic language, the Dirichlet series of Corollary 4.2 exactly evaluates the integral (6.4), as we check in the following proposition.
Proposition 6.2. Assume
![]() $\unicode[STIX]{x1D719}$
is as in Definition 1.1. Then
$\unicode[STIX]{x1D719}$
is as in Definition 1.1. Then
 $$\begin{eqnarray}I_{f}(\unicode[STIX]{x1D719},s,g_{\infty })=\frac{L(\unicode[STIX]{x1D70B},\text{Spin},s-2)}{\unicode[STIX]{x1D701}(2s-4)\unicode[STIX]{x1D701}_{D_{B}}(2s-2)}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{\infty }).\end{eqnarray}$$
$$\begin{eqnarray}I_{f}(\unicode[STIX]{x1D719},s,g_{\infty })=\frac{L(\unicode[STIX]{x1D70B},\text{Spin},s-2)}{\unicode[STIX]{x1D701}(2s-4)\unicode[STIX]{x1D701}_{D_{B}}(2s-2)}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{\infty }).\end{eqnarray}$$
Proof. If
 $\unicode[STIX]{x1D708}(g_{\infty })>0$
, one has
$\unicode[STIX]{x1D708}(g_{\infty })>0$
, one has
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{\infty })=a_{f}(T)\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{\infty })=a_{f}(T)\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)},\end{eqnarray}$$
while
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{\infty })=0$
if
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g_{\infty })=0$
if
 $\unicode[STIX]{x1D708}(g_{\infty })<0$
. Suppose
$\unicode[STIX]{x1D708}(g_{\infty })<0$
. Suppose
 $h=(\unicode[STIX]{x1D706},m)\in M_{P,6}(\mathbf{A}_{f})$
. Then
$h=(\unicode[STIX]{x1D706},m)\in M_{P,6}(\mathbf{A}_{f})$
. Then
 $h=h_{\mathbf{Q}}h_{\infty }^{-1}k$
for some
$h=h_{\mathbf{Q}}h_{\infty }^{-1}k$
for some
 $h\in M_{P,6}(\mathbf{Q})$
and
$h\in M_{P,6}(\mathbf{Q})$
and
 $k\in M_{P,6}(\mathbf{Z}_{p})$
, where
$k\in M_{P,6}(\mathbf{Z}_{p})$
, where
 $h_{\infty }=(h_{\mathbf{Q}})_{\infty }$
is the component of
$h_{\infty }=(h_{\mathbf{Q}})_{\infty }$
is the component of
![]() $h_{\mathbf{Q}}$
at the archimedean place. Hence
$h_{\mathbf{Q}}$
at the archimedean place. Hence
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(hg_{\infty })=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(h_{\mathbf{Q}}h_{\infty }^{-1}g_{\infty })=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}\cdot h_{\mathbf{Q}}}(h_{\infty }^{-1}g_{\infty })$
, where
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(hg_{\infty })=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(h_{\mathbf{Q}}h_{\infty }^{-1}g_{\infty })=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}\cdot h_{\mathbf{Q}}}(h_{\infty }^{-1}g_{\infty })$
, where
![]() $\unicode[STIX]{x1D712}\cdot h_{\mathbf{Q}}$
is the Fourier coefficient (5.6) except with
$\unicode[STIX]{x1D712}\cdot h_{\mathbf{Q}}$
is the Fourier coefficient (5.6) except with
![]() $T$
replaced by
$T$
replaced by
 $\unicode[STIX]{x1D706}m^{-1}Tc(m)$
. Thus,
$\unicode[STIX]{x1D706}m^{-1}Tc(m)$
. Thus,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(hg_{\infty }) & = & \displaystyle a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\unicode[STIX]{x1D708}(h_{\infty }^{-1}g_{\infty })^{-r}j(h_{\infty }^{-1}g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}((\unicode[STIX]{x1D706}m^{-1}Tc(m))(h_{\infty }^{-1}g_{\infty })\cdot i)}\nonumber\\ \displaystyle & = & \displaystyle a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\unicode[STIX]{x1D706}^{-3r}\det (m)^{-r}(\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(hg_{\infty }) & = & \displaystyle a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\unicode[STIX]{x1D708}(h_{\infty }^{-1}g_{\infty })^{-r}j(h_{\infty }^{-1}g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}((\unicode[STIX]{x1D706}m^{-1}Tc(m))(h_{\infty }^{-1}g_{\infty })\cdot i)}\nonumber\\ \displaystyle & = & \displaystyle a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\unicode[STIX]{x1D706}^{-3r}\det (m)^{-r}(\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)}).\nonumber\end{eqnarray}$$
Hence if
 $h\in (h_{\mathbf{Q}})_{f}M_{P,6}(\mathbf{Z}_{p})$
, with
$h\in (h_{\mathbf{Q}})_{f}M_{P,6}(\mathbf{Z}_{p})$
, with
 $h_{\mathbf{Q}}=(\unicode[STIX]{x1D706},m)$
, then the integrand in (6.4) is equal to
$h_{\mathbf{Q}}=(\unicode[STIX]{x1D706},m)$
, then the integrand in (6.4) is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D706}^{6}\det (m)^{2})\det (m)(a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\unicode[STIX]{x1D706}^{-3r}\det (m)^{-r})(\unicode[STIX]{x1D706}\det (m))^{-s-1}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m)\nonumber\\ \displaystyle & & \displaystyle \qquad \times (\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}^{-(s+3r-5)}\det (m)^{-(s+r-2)}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m)a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\times (\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D706}^{6}\det (m)^{2})\det (m)(a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\unicode[STIX]{x1D706}^{-3r}\det (m)^{-r})(\unicode[STIX]{x1D706}\det (m))^{-s-1}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m)\nonumber\\ \displaystyle & & \displaystyle \qquad \times (\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D706}^{-(s+3r-5)}\det (m)^{-(s+r-2)}\unicode[STIX]{x1D6EF}(\unicode[STIX]{x1D706},m)a_{f}(\unicode[STIX]{x1D706}m^{-1}Tc(m))\times (\unicode[STIX]{x1D708}(g_{\infty })^{-r}j(g_{\infty },i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg_{\infty }\cdot i)}).\nonumber\end{eqnarray}$$
Applying Corollary 4.2 and (6.5) again gives the proposition. ◻
6.2 The infinite place
Suppose
![]() $\unicode[STIX]{x1D719}$
is a cusp form corresponding to a level-one, holomorphic Siegel modular form of weight
$\unicode[STIX]{x1D719}$
is a cusp form corresponding to a level-one, holomorphic Siegel modular form of weight
![]() $2r$
, as in Definition 1.1. We now compute the normalized archimedean integral
$2r$
, as in Definition 1.1. We now compute the normalized archimedean integral
 $$\begin{eqnarray}I_{\infty ,2r}^{\ast }(\unicode[STIX]{x1D719},s)=\unicode[STIX]{x1D70B}^{-(s+r)}D_{B}^{s}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-8)I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s),\end{eqnarray}$$
$$\begin{eqnarray}I_{\infty ,2r}^{\ast }(\unicode[STIX]{x1D719},s)=\unicode[STIX]{x1D70B}^{-(s+r)}D_{B}^{s}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-8)I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s),\end{eqnarray}$$
where
 $$\begin{eqnarray}I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{U_{0}(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)|\unicode[STIX]{x1D708}(g)|^{s}\unicode[STIX]{x1D6F7}_{\infty ,2r}(f_{{\mathcal{O}}}g)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=\int _{U_{0}(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)|\unicode[STIX]{x1D708}(g)|^{s}\unicode[STIX]{x1D6F7}_{\infty ,2r}(f_{{\mathcal{O}}}g)\,dg.\end{eqnarray}$$
We prove the following theorem.
Theorem 6.3. Suppose
![]() $\unicode[STIX]{x1D719}$
is as in Definition 1.1, and that
$\unicode[STIX]{x1D719}$
is as in Definition 1.1, and that
![]() $\unicode[STIX]{x1D719}$
corresponds to the level-one Siegel modular form
$\unicode[STIX]{x1D719}$
corresponds to the level-one Siegel modular form
![]() $f$
. Then
$f$
. Then
 $I_{\infty ,2r}^{\ast }(\unicode[STIX]{x1D719},s)$
equals
$I_{\infty ,2r}^{\ast }(\unicode[STIX]{x1D719},s)$
equals
 $$\begin{eqnarray}a_{f}(T)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-4)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-3)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-2)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+3r-5)\end{eqnarray}$$
$$\begin{eqnarray}a_{f}(T)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-4)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-3)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-2)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+3r-5)\end{eqnarray}$$
up to a nonzero constant.
Our first task is to define the Schwartz function
![]() $\unicode[STIX]{x1D6F7}_{\infty ,2r}$
on
$\unicode[STIX]{x1D6F7}_{\infty ,2r}$
on
![]() $W(\mathbf{R})$
. To do this, we digress slightly and discuss the Hermitian symmetric space
$W(\mathbf{R})$
. To do this, we digress slightly and discuss the Hermitian symmetric space
![]() ${\mathcal{H}}$
associated to
${\mathcal{H}}$
associated to
![]() $\text{G}(\mathbf{R})$
.
$\text{G}(\mathbf{R})$
.
6.2.1 The Hermitian symmetric space for
 $\text{G}(\mathbf{R})$
$\text{G}(\mathbf{R})$
We assume
 $B_{\mathbf{R}}=B\otimes \mathbf{R}$
is the Hamilton quaternions. Set
$B_{\mathbf{R}}=B\otimes \mathbf{R}$
is the Hamilton quaternions. Set
 $B_{\mathbf{C}}=B_{\mathbf{R}}\otimes _{\mathbf{R}}\mathbf{C}$
, with the involution on
$B_{\mathbf{C}}=B_{\mathbf{R}}\otimes _{\mathbf{R}}\mathbf{C}$
, with the involution on
![]() $B_{\mathbf{C}}$
the one from
$B_{\mathbf{C}}$
the one from
![]() $B_{\mathbf{R}}$
, extended
$B_{\mathbf{R}}$
, extended
![]() $\mathbf{C}$
-linearly to
$\mathbf{C}$
-linearly to
![]() $B_{\mathbf{C}}$
. Associated to
$B_{\mathbf{C}}$
. Associated to
![]() $B_{\mathbf{C}}$
, we have the space
$B_{\mathbf{C}}$
, we have the space
 $H_{3}(B_{\mathbf{C}})$
of
$H_{3}(B_{\mathbf{C}})$
of
![]() $3\times 3$
Hermitian matrices over
$3\times 3$
Hermitian matrices over
![]() $B_{\mathbf{C}}$
. Elements of
$B_{\mathbf{C}}$
. Elements of
 $H_{3}(B_{\mathbf{C}})$
are formal expressions
$H_{3}(B_{\mathbf{C}})$
are formal expressions
 $Z=X+iY$
, with
$Z=X+iY$
, with
![]() $X,Y$
in
$X,Y$
in
 $H_{3}(B_{\mathbf{R}})$
. Note that the
$H_{3}(B_{\mathbf{R}})$
. Note that the
![]() $i$
in this expression is not the
$i$
in this expression is not the
![]() $i$
in
$i$
in
![]() $B_{\mathbf{R}}$
; this
$B_{\mathbf{R}}$
; this
![]() $i$
is in the center of
$i$
is in the center of
![]() $B_{\mathbf{C}}$
. The Hermitian symmetric space
$B_{\mathbf{C}}$
. The Hermitian symmetric space
![]() ${\mathcal{H}}$
is the set of
${\mathcal{H}}$
is the set of
 $Z=X+iY$
in
$Z=X+iY$
in
 $H_{3}(B_{\mathbf{C}})$
with
$H_{3}(B_{\mathbf{C}})$
with
![]() $Y$
positive definite.
$Y$
positive definite.
Denote by
![]() $\text{G}^{+}(\mathbf{R})$
the subgroup of
$\text{G}^{+}(\mathbf{R})$
the subgroup of
![]() $\text{G}(\mathbf{R})$
that is the connected component of the identity. We explain the action of
$\text{G}(\mathbf{R})$
that is the connected component of the identity. We explain the action of
![]() $\text{G}^{+}(\mathbf{R})$
on
$\text{G}^{+}(\mathbf{R})$
on
![]() ${\mathcal{H}}$
. First, note that we have an inclusion
${\mathcal{H}}$
. First, note that we have an inclusion
 $\text{G}(\mathbf{R})\rightarrow \text{G}(\mathbf{C})$
, and
$\text{G}(\mathbf{R})\rightarrow \text{G}(\mathbf{C})$
, and
![]() $\text{G}(\mathbf{C})$
acts on
$\text{G}(\mathbf{C})$
acts on
 $W(\mathbf{C})=W(\mathbf{R})\otimes _{\mathbf{R}}\mathbf{C}$
. Set
$W(\mathbf{C})=W(\mathbf{R})\otimes _{\mathbf{R}}\mathbf{C}$
. Set
 $e=(1,0,0,0)$
, a rank-one element of
$e=(1,0,0,0)$
, a rank-one element of
![]() $W$
. Identify
$W$
. Identify
![]() $Z\in {\mathcal{H}}$
with the rank-one element
$Z\in {\mathcal{H}}$
with the rank-one element
 $$\begin{eqnarray}r(Z)=en(-Z)=(1,-Z,Z^{\sharp },-N(Z)).\end{eqnarray}$$
$$\begin{eqnarray}r(Z)=en(-Z)=(1,-Z,Z^{\sharp },-N(Z)).\end{eqnarray}$$
Consider the projective space
 $\mathbf{P}(W(\mathbf{C})^{rk=1})$
of rank-one
$\mathbf{P}(W(\mathbf{C})^{rk=1})$
of rank-one
![]() $\mathbf{C}$
-lines in
$\mathbf{C}$
-lines in
![]() $W(\mathbf{C})$
. Then
$W(\mathbf{C})$
. Then
![]() $\text{G}(\mathbf{R})$
acts on this space on the left via
$\text{G}(\mathbf{R})$
acts on this space on the left via
 $g\cdot v=vg^{-1}$
. We will see momentarily that
$g\cdot v=vg^{-1}$
. We will see momentarily that
![]() $\text{G}^{+}(\mathbf{R})$
preserves the image of
$\text{G}^{+}(\mathbf{R})$
preserves the image of
![]() ${\mathcal{H}}$
inside
${\mathcal{H}}$
inside
 $\mathbf{P}(W(\mathbf{C})^{rk=1})$
, and acts on it transitively. In fact, the factor of automorphy
$\mathbf{P}(W(\mathbf{C})^{rk=1})$
, and acts on it transitively. In fact, the factor of automorphy
 $$\begin{eqnarray}j_{\text{G}(\mathbf{R})}(g,Z):\text{G}^{+}(\mathbf{R})\times {\mathcal{H}}\rightarrow \mathbf{C}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}j_{\text{G}(\mathbf{R})}(g,Z):\text{G}^{+}(\mathbf{R})\times {\mathcal{H}}\rightarrow \mathbf{C}^{\times }\end{eqnarray}$$
and the action of
![]() $\text{G}^{+}(\mathbf{R})$
on
$\text{G}^{+}(\mathbf{R})$
on
![]() ${\mathcal{H}}$
are simultaneously defined by the equality
${\mathcal{H}}$
are simultaneously defined by the equality
 $$\begin{eqnarray}r(Z)g^{-1}=j_{\text{G}(\mathbf{R})}(g,Z)r(gZ).\end{eqnarray}$$
$$\begin{eqnarray}r(Z)g^{-1}=j_{\text{G}(\mathbf{R})}(g,Z)r(gZ).\end{eqnarray}$$
We summarize what we need in a proposition. Recall the rank-one element
 $f=(0,0,0,1)$
.
$f=(0,0,0,1)$
.
Proposition 6.4. Suppose
![]() $Z\in {\mathcal{H}}$
, and
$Z\in {\mathcal{H}}$
, and
 $g\in \text{G}^{+}(\mathbf{R})$
. Then the complex number
$g\in \text{G}^{+}(\mathbf{R})$
. Then the complex number
 $j_{\text{G}(\mathbf{R})}(g,Z)=\langle r(Z)g^{-1},f\rangle$
is nonzero, and thus
$j_{\text{G}(\mathbf{R})}(g,Z)=\langle r(Z)g^{-1},f\rangle$
is nonzero, and thus
 $$\begin{eqnarray}r(Z)g^{-1}=j_{\text{G}(\mathbf{R})}(g,Z)r(gZ)\end{eqnarray}$$
$$\begin{eqnarray}r(Z)g^{-1}=j_{\text{G}(\mathbf{R})}(g,Z)r(gZ)\end{eqnarray}$$
for some
![]() $gZ$
in
$gZ$
in
 $H_{3}(B_{\mathbf{C}})$
. The element
$H_{3}(B_{\mathbf{C}})$
. The element
![]() $gZ$
is in
$gZ$
is in
![]() ${\mathcal{H}}$
, and thus this equality defines an action of
${\mathcal{H}}$
, and thus this equality defines an action of
![]() $\text{G}^{+}(\mathbf{R})$
on
$\text{G}^{+}(\mathbf{R})$
on
![]() ${\mathcal{H}}$
. Under the natural embedding
${\mathcal{H}}$
. Under the natural embedding
 ${\mathcal{H}}_{3}\rightarrow {\mathcal{H}}$
, the two actions of
${\mathcal{H}}_{3}\rightarrow {\mathcal{H}}$
, the two actions of
 $\operatorname{GSp}_{6}^{+}(\mathbf{R})$
are the same. Furthermore,
$\operatorname{GSp}_{6}^{+}(\mathbf{R})$
are the same. Furthermore,
 $j_{\operatorname{GSp}_{6}}(g,Z)=j_{\text{G}(\mathbf{R})}(g,Z)$
when
$j_{\operatorname{GSp}_{6}}(g,Z)=j_{\text{G}(\mathbf{R})}(g,Z)$
when
 $g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
and
$g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
and
![]() $Z\in {\mathcal{H}}_{3}$
.
$Z\in {\mathcal{H}}_{3}$
.
Proof. We sketch the proof. First, a minimal parabolic subgroup
![]() $P_{0}$
of
$P_{0}$
of
![]() $\text{G}$
is discussed in § 7.1. One can check that the subgroup
$\text{G}$
is discussed in § 7.1. One can check that the subgroup
![]() $P_{0}^{+}(\mathbf{R})$
of
$P_{0}^{+}(\mathbf{R})$
of
![]() $\text{G}^{+}(\mathbf{R})$
has
$\text{G}^{+}(\mathbf{R})$
has
 $j_{\text{G}(\mathbf{R})}(P_{0}^{+}(\mathbf{R}),{\mathcal{H}})\neq 0$
and acts transitively on
$j_{\text{G}(\mathbf{R})}(P_{0}^{+}(\mathbf{R}),{\mathcal{H}})\neq 0$
and acts transitively on
![]() ${\mathcal{H}}$
. Now suppose
${\mathcal{H}}$
. Now suppose
 $g\in \text{G}^{+}(\mathbf{R})$
,
$g\in \text{G}^{+}(\mathbf{R})$
,
![]() $Z\in {\mathcal{H}}$
, and
$Z\in {\mathcal{H}}$
, and
 $p\in P_{0}^{+}(\mathbf{R})$
satisfies
$p\in P_{0}^{+}(\mathbf{R})$
satisfies
 $p\cdot i=Z$
. Then
$p\cdot i=Z$
. Then
 $$\begin{eqnarray}\langle r(Z)g^{-1},f\rangle =j_{\text{G}(\mathbf{R})}(p,i)^{-1}\langle r(i)p^{-1}g^{-1},f\rangle =\unicode[STIX]{x1D708}(gp)^{-1}j_{\text{G}(\mathbf{R})}(p,i)^{-1}\langle r(i),fgp\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\langle r(Z)g^{-1},f\rangle =j_{\text{G}(\mathbf{R})}(p,i)^{-1}\langle r(i)p^{-1}g^{-1},f\rangle =\unicode[STIX]{x1D708}(gp)^{-1}j_{\text{G}(\mathbf{R})}(p,i)^{-1}\langle r(i),fgp\rangle .\end{eqnarray}$$
This last quantity is then nonzero by Lemma 6.5 below. Hence
 $r(Z)g^{-1}=j_{\text{G}(\mathbf{R})}(g,Z)r(gZ)$
for some
$r(Z)g^{-1}=j_{\text{G}(\mathbf{R})}(g,Z)r(gZ)$
for some
![]() $gZ$
in
$gZ$
in
 $H_{3}(B_{\mathbf{C}})$
. Next, one verifies the equality
$H_{3}(B_{\mathbf{C}})$
. Next, one verifies the equality
 $N(\operatorname{Im}(W))=(1/8i)\langle \overline{r(W)},r(W)\rangle$
for any
$N(\operatorname{Im}(W))=(1/8i)\langle \overline{r(W)},r(W)\rangle$
for any
 $W\in H_{3}(B_{\mathbf{C}})$
. One deduces from this equality that
$W\in H_{3}(B_{\mathbf{C}})$
. One deduces from this equality that
 $N(\operatorname{Im}(gZ))>0$
. Then that
$N(\operatorname{Im}(gZ))>0$
. Then that
 $gZ\in {\mathcal{H}}$
follows from a continuity argument.
$gZ\in {\mathcal{H}}$
follows from a continuity argument.
To check that the actions and factors of automorphy agree for
 $g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
and
$g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
and
![]() $Z\in {\mathcal{H}}_{3}$
, it suffices to check this on generators
$Z\in {\mathcal{H}}_{3}$
, it suffices to check this on generators
 $n(X),J_{6}$
and
$n(X),J_{6}$
and
 $M_{P,6}^{+}(\mathbf{R})$
, which may be done easily.◻
$M_{P,6}^{+}(\mathbf{R})$
, which may be done easily.◻
Before defining
![]() $\unicode[STIX]{x1D6F7}_{\infty ,2r}$
, we need an additional lemma. Recall the element
$\unicode[STIX]{x1D6F7}_{\infty ,2r}$
, we need an additional lemma. Recall the element
![]() $J$
of
$J$
of
![]() $\text{G}(\mathbf{Q})$
that sends
$\text{G}(\mathbf{Q})$
that sends
 $(a,b,c,d)\mapsto (-d,c,-b,a)$
.
$(a,b,c,d)\mapsto (-d,c,-b,a)$
.
Lemma 6.5. If
 $v=(a,b,c,d)$
, define
$v=(a,b,c,d)$
, define
 $\Vert v\Vert ^{2}=\langle v,vJ\rangle$
. Then
$\Vert v\Vert ^{2}=\langle v,vJ\rangle$
. Then
 $\Vert v\Vert ^{2}=a^{2}+\operatorname{tr}(b,b)+\operatorname{tr}(c,c)+d^{2}$
, and hence if
$\Vert v\Vert ^{2}=a^{2}+\operatorname{tr}(b,b)+\operatorname{tr}(c,c)+d^{2}$
, and hence if
 $v\in W(\mathbf{R})$
,
$v\in W(\mathbf{R})$
,
 $\Vert v\Vert ^{2}\geqslant 0$
and is only
$\Vert v\Vert ^{2}\geqslant 0$
and is only
![]() $0$
when
$0$
when
![]() $v=0$
. If furthermore
$v=0$
. If furthermore
![]() $v$
is of rank one, then
$v$
is of rank one, then
 $|\langle r(i),v\rangle |^{2}=\Vert v\Vert ^{2}$
.
$|\langle r(i),v\rangle |^{2}=\Vert v\Vert ^{2}$
.
Proof. The formula for
![]() $\Vert v\Vert ^{2}$
is trivial. Suppose
$\Vert v\Vert ^{2}$
is trivial. Suppose
![]() $v$
is rank one. We have
$v$
is rank one. We have
 $\langle r(i),v\rangle =(d-\operatorname{tr}(b))+i(\operatorname{tr}(c)-a)$
. Hence
$\langle r(i),v\rangle =(d-\operatorname{tr}(b))+i(\operatorname{tr}(c)-a)$
. Hence
 $$\begin{eqnarray}\displaystyle |\langle r(i),v\rangle |^{2} & = & \displaystyle (d-\operatorname{tr}(b))^{2}+(a-\operatorname{tr}(c))^{2}\nonumber\\ \displaystyle & = & \displaystyle d^{2}-2\,d\operatorname{tr}(b)+\operatorname{tr}(b)^{2}+a^{2}-2a\operatorname{tr}(c)+\operatorname{tr}(c)^{2}\nonumber\\ \displaystyle & = & \displaystyle a^{2}+(\operatorname{tr}(b)^{2}-2\operatorname{tr}(b^{\sharp }))+(\operatorname{tr}(c)^{2}-2\operatorname{tr}(c^{\sharp }))+d^{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |\langle r(i),v\rangle |^{2} & = & \displaystyle (d-\operatorname{tr}(b))^{2}+(a-\operatorname{tr}(c))^{2}\nonumber\\ \displaystyle & = & \displaystyle d^{2}-2\,d\operatorname{tr}(b)+\operatorname{tr}(b)^{2}+a^{2}-2a\operatorname{tr}(c)+\operatorname{tr}(c)^{2}\nonumber\\ \displaystyle & = & \displaystyle a^{2}+(\operatorname{tr}(b)^{2}-2\operatorname{tr}(b^{\sharp }))+(\operatorname{tr}(c)^{2}-2\operatorname{tr}(c^{\sharp }))+d^{2},\nonumber\end{eqnarray}$$
where in the last equality, since
![]() $v$
is rank one,
$v$
is rank one,
![]() $db=c^{\sharp }$
and
$db=c^{\sharp }$
and
![]() $ac=b^{\sharp }$
. For general
$ac=b^{\sharp }$
. For general
![]() $W$
one has the equality
$W$
one has the equality
 $\operatorname{tr}(W)^{2}-2\operatorname{tr}(W^{\sharp })=\operatorname{tr}(W,W)$
. The lemma follows.◻
$\operatorname{tr}(W)^{2}-2\operatorname{tr}(W^{\sharp })=\operatorname{tr}(W,W)$
. The lemma follows.◻
6.2.2 Archimedean calculation
Define
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\infty ,2r}(v)=e^{-\Vert v\Vert ^{2}}\langle r(i),v\rangle ^{2r}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\infty ,2r}(v)=e^{-\Vert v\Vert ^{2}}\langle r(i),v\rangle ^{2r}.\end{eqnarray}$$
This is obviously a Schwartz function on
![]() $W(\mathbf{R})$
. Note that we have
$W(\mathbf{R})$
. Note that we have
 $\langle r(i),vgk\rangle =j(k,i)\langle r(i),vg\rangle$
for
$\langle r(i),vgk\rangle =j(k,i)\langle r(i),vg\rangle$
for
![]() $k$
in
$k$
in
![]() $K_{\infty ,\operatorname{Sp}_{6}}$
. Our assumption on
$K_{\infty ,\operatorname{Sp}_{6}}$
. Our assumption on
![]() $\unicode[STIX]{x1D719}$
gives
$\unicode[STIX]{x1D719}$
gives
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)=a_{f}(T)\unicode[STIX]{x1D708}(g)^{-r}j(g,i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg\cdot i)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)=a_{f}(T)\unicode[STIX]{x1D708}(g)^{-r}j(g,i)^{-2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Tg\cdot i)}\end{eqnarray}$$
if
 $g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
, and
$g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
, and
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)=0$
if
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)=0$
if
 $\unicode[STIX]{x1D708}(g)<0$
. (The modular form associated to
$\unicode[STIX]{x1D708}(g)<0$
. (The modular form associated to
![]() $\unicode[STIX]{x1D719}$
has negative definite Fourier coefficients when restricted to the lower half-space,
$\unicode[STIX]{x1D719}$
has negative definite Fourier coefficients when restricted to the lower half-space,
![]() ${\mathcal{H}}_{3}^{-}$
.) Furthermore, for
${\mathcal{H}}_{3}^{-}$
.) Furthermore, for
 $g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
, one has the identity
$g\in \operatorname{GSp}_{6}^{+}(\mathbf{R})$
, one has the identity
 $$\begin{eqnarray}\unicode[STIX]{x1D708}(g)^{-1}j(g,i)^{-1}\langle r(i),f_{{\mathcal{O}}}g\rangle =\operatorname{tr}(T(g\cdot i)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(g)^{-1}j(g,i)^{-1}\langle r(i),f_{{\mathcal{O}}}g\rangle =\operatorname{tr}(T(g\cdot i)).\end{eqnarray}$$
Note that the left-hand side of (6.8), as a function of
![]() $g$
, is right
$g$
, is right
 $Z(\mathbf{R})K_{\infty ,\operatorname{Sp}_{6}}$
-invariant. Hence to prove the equality, it suffices to take
$Z(\mathbf{R})K_{\infty ,\operatorname{Sp}_{6}}$
-invariant. Hence to prove the equality, it suffices to take
![]() $g$
in the Siegel parabolic of
$g$
in the Siegel parabolic of
![]() $\operatorname{GSp}_{6}$
, and then (6.8) follows from (6.2).
$\operatorname{GSp}_{6}$
, and then (6.8) follows from (6.2).
Now, putting (6.7) into (6.6) and integrating over the center
![]() $Z(\mathbf{R})$
, we obtain
$Z(\mathbf{R})$
, we obtain
 $$\begin{eqnarray}\displaystyle I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s) & = & \displaystyle \unicode[STIX]{x1D6E4}(s+r)\int _{U^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}\frac{|\unicode[STIX]{x1D708}(g)|^{s}\langle r(i),f_{{\mathcal{O}}}g\rangle ^{2r}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)}{|\langle r(i),f_{{\mathcal{O}}}g\rangle |^{2s+2r}}\,dg\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E4}(s+r)\int _{U^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}^{+}(\mathbf{R})}a(T)\frac{|\unicode[STIX]{x1D708}(g)|^{s+r}\operatorname{tr}(TZ)^{2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(TZ)}}{|\langle r(i),f_{{\mathcal{O}}}g\rangle |^{2s+2r}}\,dg,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s) & = & \displaystyle \unicode[STIX]{x1D6E4}(s+r)\int _{U^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}(\mathbf{R})}\frac{|\unicode[STIX]{x1D708}(g)|^{s}\langle r(i),f_{{\mathcal{O}}}g\rangle ^{2r}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D712}}(g)}{|\langle r(i),f_{{\mathcal{O}}}g\rangle |^{2s+2r}}\,dg\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E4}(s+r)\int _{U^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}^{+}(\mathbf{R})}a(T)\frac{|\unicode[STIX]{x1D708}(g)|^{s+r}\operatorname{tr}(TZ)^{2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(TZ)}}{|\langle r(i),f_{{\mathcal{O}}}g\rangle |^{2s+2r}}\,dg,\nonumber\end{eqnarray}$$
where
 $Z=g\cdot i=X+iY$
. One has
$Z=g\cdot i=X+iY$
. One has
 $$\begin{eqnarray}\frac{|\unicode[STIX]{x1D708}(g)|^{s+r}}{|\langle r(i),f_{{\mathcal{O}}}g\rangle |^{2s+2r}}=\frac{|\unicode[STIX]{x1D708}(g)^{-1}j(g,i)^{-2}|^{s+r}}{|\operatorname{tr}(TZ)|^{2s+2r}}=\frac{N(Y)^{s+r}}{|\operatorname{tr}(TZ)|^{2s+2r}}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{|\unicode[STIX]{x1D708}(g)|^{s+r}}{|\langle r(i),f_{{\mathcal{O}}}g\rangle |^{2s+2r}}=\frac{|\unicode[STIX]{x1D708}(g)^{-1}j(g,i)^{-2}|^{s+r}}{|\operatorname{tr}(TZ)|^{2s+2r}}=\frac{N(Y)^{s+r}}{|\operatorname{tr}(TZ)|^{2s+2r}}.\end{eqnarray}$$
Hence,
 $I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=a(T)\unicode[STIX]{x1D6E4}(s+r)N(T)^{-(s+r)}J(s)$
, with
$I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=a(T)\unicode[STIX]{x1D6E4}(s+r)N(T)^{-(s+r)}J(s)$
, with
 $$\begin{eqnarray}\displaystyle J(s) & = & \displaystyle \int _{U^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}^{+}(\mathbf{R})}\frac{N(TY)^{s+r}\operatorname{tr}(TZ)^{2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(TZ)}}{|\operatorname{tr}(TZ)|^{2s+2r}}\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{1}^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}^{+}(\mathbf{R})}\frac{N(Y)^{s+r}\operatorname{tr}(Z)^{2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Z)}}{|\operatorname{tr}(Z)|^{2s+2r}}\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J(s) & = & \displaystyle \int _{U^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}^{+}(\mathbf{R})}\frac{N(TY)^{s+r}\operatorname{tr}(TZ)^{2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(TZ)}}{|\operatorname{tr}(TZ)|^{2s+2r}}\,dg\nonumber\\ \displaystyle & = & \displaystyle \int _{U_{1}^{0}(\mathbf{R})Z(\mathbf{R})\backslash \!\operatorname{GSp}_{6}^{+}(\mathbf{R})}\frac{N(Y)^{s+r}\operatorname{tr}(Z)^{2r}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Z)}}{|\operatorname{tr}(Z)|^{2s+2r}}\,dg,\end{eqnarray}$$
where
 $U_{1}^{0}=\{(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!):\operatorname{tr}(X)=0\}$
. The change of variables implicit in equality (6.9) is
$U_{1}^{0}=\{(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!):\operatorname{tr}(X)=0\}$
. The change of variables implicit in equality (6.9) is
 $g=m_{T}^{-1}g^{\prime }$
, where
$g=m_{T}^{-1}g^{\prime }$
, where
 $m_{T}=(\!\begin{smallmatrix}T^{1/2} & \\ & T^{-1/2}\end{smallmatrix}\!)$
and
$m_{T}=(\!\begin{smallmatrix}T^{1/2} & \\ & T^{-1/2}\end{smallmatrix}\!)$
and
![]() $T^{1/2}$
a positive-definite symmetric square root of
$T^{1/2}$
a positive-definite symmetric square root of
![]() $T$
.
$T$
.
We now explain how to compute the integral
![]() $J(s)$
. As the global integral representation is an analogue of Garrett’s triple product [Reference GarrettGar87], we follow the archimedean calculation of [Reference GarrettGar87]. We compute up to nonzero constants. First, we have that
$J(s)$
. As the global integral representation is an analogue of Garrett’s triple product [Reference GarrettGar87], we follow the archimedean calculation of [Reference GarrettGar87]. We compute up to nonzero constants. First, we have that
 $$\begin{eqnarray}J(s)=\int _{Z(\mathbf{R})\backslash M_{P,6}^{+}(\mathbf{R})}N(Y)^{s+r-2}e^{-2\unicode[STIX]{x1D70B}\operatorname{tr}(Y)}\int _{\mathbf{R}}\frac{(x+i\operatorname{tr}(Y))^{2r}}{|x+i\operatorname{tr}(Y)|^{2s+2r}}e^{2\unicode[STIX]{x1D70B}ix}\,dx\,d^{\ast }Y.\end{eqnarray}$$
$$\begin{eqnarray}J(s)=\int _{Z(\mathbf{R})\backslash M_{P,6}^{+}(\mathbf{R})}N(Y)^{s+r-2}e^{-2\unicode[STIX]{x1D70B}\operatorname{tr}(Y)}\int _{\mathbf{R}}\frac{(x+i\operatorname{tr}(Y))^{2r}}{|x+i\operatorname{tr}(Y)|^{2s+2r}}e^{2\unicode[STIX]{x1D70B}ix}\,dx\,d^{\ast }Y.\end{eqnarray}$$
Here
![]() $d^{\ast }Y$
is the
$d^{\ast }Y$
is the
 $M_{P,6}^{+}(\mathbf{R})$
invariant measure on
$M_{P,6}^{+}(\mathbf{R})$
invariant measure on
![]() $Y$
, and we have used that
$Y$
, and we have used that
 $\unicode[STIX]{x1D6FF}_{P}(g)=\det (Y)^{2}$
for
$\unicode[STIX]{x1D6FF}_{P}(g)=\det (Y)^{2}$
for
 $g\in M_{P,6}^{+}(\mathbf{R})$
. Making a variable change, the inner integral becomes
$g\in M_{P,6}^{+}(\mathbf{R})$
. Making a variable change, the inner integral becomes
 $$\begin{eqnarray}\operatorname{tr}(Y)^{1-2s}\int _{\mathbf{R}}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Y)x}\,dx,\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{tr}(Y)^{1-2s}\int _{\mathbf{R}}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}e^{2\unicode[STIX]{x1D70B}i\operatorname{tr}(Y)x}\,dx,\end{eqnarray}$$
using that
![]() $\operatorname{tr}(Y)$
is positive. We now introduce a
$\operatorname{tr}(Y)$
is positive. We now introduce a
![]() $\unicode[STIX]{x1D6E4}$
-integral, and change the order of integration to obtain
$\unicode[STIX]{x1D6E4}$
-integral, and change the order of integration to obtain
 $$\begin{eqnarray}\displaystyle (2\unicode[STIX]{x1D70B})^{1-2s}\unicode[STIX]{x1D6E4}(2s-1)J(s) & = & \displaystyle \int _{\mathbf{R}}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}\int _{Y}N(Y)^{s+r-2}e^{2\unicode[STIX]{x1D70B}i(x+i)\operatorname{tr}(Y)}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{t\geqslant 0}e^{-2\unicode[STIX]{x1D70B}t\operatorname{tr}(Y)}t^{2s-1}\,\frac{dt}{t}\biggr)\,d^{\ast }Y\,dx.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (2\unicode[STIX]{x1D70B})^{1-2s}\unicode[STIX]{x1D6E4}(2s-1)J(s) & = & \displaystyle \int _{\mathbf{R}}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}\int _{Y}N(Y)^{s+r-2}e^{2\unicode[STIX]{x1D70B}i(x+i)\operatorname{tr}(Y)}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{t\geqslant 0}e^{-2\unicode[STIX]{x1D70B}t\operatorname{tr}(Y)}t^{2s-1}\,\frac{dt}{t}\biggr)\,d^{\ast }Y\,dx.\nonumber\end{eqnarray}$$
Define a logarithm on
![]() $\mathbf{C}$
by removing the nonpositive reals, and use this logarithm to define
$\mathbf{C}$
by removing the nonpositive reals, and use this logarithm to define
![]() $z^{s}$
for such a
$z^{s}$
for such a
![]() $z$
. Then switching the order of integration we obtain
$z$
. Then switching the order of integration we obtain
 $$\begin{eqnarray}\displaystyle (2\unicode[STIX]{x1D70B})^{1-2s}\unicode[STIX]{x1D6E4}(2s-1)J(s) & = & \displaystyle \int _{\mathbf{R}}\int _{t\geqslant 0}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}(1+t-ix)^{-3(s+r-2)}t^{2s-1}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{Y}N(Y^{\prime })^{s+r-2}e^{-2\unicode[STIX]{x1D70B}\operatorname{tr}(Y^{\prime })}\,d^{\ast }(Y^{\prime })\biggr)\,\frac{dt}{t}\,dx,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (2\unicode[STIX]{x1D70B})^{1-2s}\unicode[STIX]{x1D6E4}(2s-1)J(s) & = & \displaystyle \int _{\mathbf{R}}\int _{t\geqslant 0}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}(1+t-ix)^{-3(s+r-2)}t^{2s-1}\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\int _{Y}N(Y^{\prime })^{s+r-2}e^{-2\unicode[STIX]{x1D70B}\operatorname{tr}(Y^{\prime })}\,d^{\ast }(Y^{\prime })\biggr)\,\frac{dt}{t}\,dx,\nonumber\end{eqnarray}$$
where
 $Y^{\prime }=(1+t-ix)Y$
. The integral over
$Y^{\prime }=(1+t-ix)Y$
. The integral over
![]() $Y$
is the so-called Siegel integral, and it is a nonzero constant times
$Y$
is the so-called Siegel integral, and it is a nonzero constant times
 $$\begin{eqnarray}2^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6).\end{eqnarray}$$
$$\begin{eqnarray}2^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6).\end{eqnarray}$$
See, for instance, [Reference Faraut and KorányiFK94, Theorem VII.1.1] for this fact.
We are thus left to evaluate the integral
 $$\begin{eqnarray}K(s,r)=\int _{\mathbf{R}}\int _{t\geqslant 0}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}(1+t-ix)^{-3(s+r-2)}t^{2s-1}\frac{dt}{t}\,dx,\end{eqnarray}$$
$$\begin{eqnarray}K(s,r)=\int _{\mathbf{R}}\int _{t\geqslant 0}\frac{(x+i)^{2r}}{|x+i|^{2s+2r}}(1+t-ix)^{-3(s+r-2)}t^{2s-1}\frac{dt}{t}\,dx,\end{eqnarray}$$
which may be done exactly as in [Reference GarrettGar87, Proof of Proposition 5.1]. Up to a nonzero constant, one obtains
 $$\begin{eqnarray}K(s,r)=2^{-(3s+3r-6)}\frac{\unicode[STIX]{x1D6E4}(s+3r-5)\unicode[STIX]{x1D6E4}(2s-1)}{\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(2s+2r-5)}.\end{eqnarray}$$
$$\begin{eqnarray}K(s,r)=2^{-(3s+3r-6)}\frac{\unicode[STIX]{x1D6E4}(s+3r-5)\unicode[STIX]{x1D6E4}(2s-1)}{\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(2s+2r-5)}.\end{eqnarray}$$
Thus, again up to nonzero constants,
 $$\begin{eqnarray}J(s)=(2\unicode[STIX]{x1D70B})^{2s-1}4^{-(3s+3r-6)}\frac{\unicode[STIX]{x1D6E4}(s+3r-5)}{\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(2s+2r-5)}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6).\end{eqnarray}$$
$$\begin{eqnarray}J(s)=(2\unicode[STIX]{x1D70B})^{2s-1}4^{-(3s+3r-6)}\frac{\unicode[STIX]{x1D6E4}(s+3r-5)}{\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(2s+2r-5)}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6).\end{eqnarray}$$
Via the duplication formula
 $\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)=\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s+2r-5)$
,
$\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)=\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s+2r-5)$
,
![]() $J(s)$
simplifies to
$J(s)$
simplifies to
 $$\begin{eqnarray}4^{-(3s+3r-6)}\frac{\unicode[STIX]{x1D6E4}(s+3r-5)}{\unicode[STIX]{x1D6E4}(s+r)}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6),\end{eqnarray}$$
$$\begin{eqnarray}4^{-(3s+3r-6)}\frac{\unicode[STIX]{x1D6E4}(s+3r-5)}{\unicode[STIX]{x1D6E4}(s+r)}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6),\end{eqnarray}$$
again up to nonzero constants. Hence
 $I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=a(T)D_{B}^{-s}4^{-(2s+2r-6)}\unicode[STIX]{x1D6E4}(s+3r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6)$
, since
$I_{\infty ,2r}^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D719},s)=a(T)D_{B}^{-s}4^{-(2s+2r-6)}\unicode[STIX]{x1D6E4}(s+3r-5)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-6)$
, since
 $D_{B}=4N(T)$
by Corollary 3.4. Thus, up to a nonzero constant,
$D_{B}=4N(T)$
by Corollary 3.4. Thus, up to a nonzero constant,
 $$\begin{eqnarray}I_{\infty ,2r}^{\ast }(\unicode[STIX]{x1D719},s)=a(T)\unicode[STIX]{x1D6E4}_{\boldsymbol{ C}}(s+r-4)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-3)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-2)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+3r-5),\end{eqnarray}$$
$$\begin{eqnarray}I_{\infty ,2r}^{\ast }(\unicode[STIX]{x1D719},s)=a(T)\unicode[STIX]{x1D6E4}_{\boldsymbol{ C}}(s+r-4)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-3)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+r-2)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s+3r-5),\end{eqnarray}$$
completing the proof of Theorem 6.3.
7 The group
 $\text{G}(\mathbf{A})$
and its Siegel Eisenstein series
$\text{G}(\mathbf{A})$
and its Siegel Eisenstein series
The purpose of this section is to prove Theorem 5.2, where
![]() $\unicode[STIX]{x1D6F7}_{2r,\infty }$
is defined in (6.7). We will prove this theorem by first proving it for
$\unicode[STIX]{x1D6F7}_{2r,\infty }$
is defined in (6.7). We will prove this theorem by first proving it for
 $E_{0}^{\ast }(g,s)$
, the Eisenstein series that is spherical at all places. Then we will define essentially a Maass–Shimura differential operator
$E_{0}^{\ast }(g,s)$
, the Eisenstein series that is spherical at all places. Then we will define essentially a Maass–Shimura differential operator
![]() ${\mathcal{D}}$
, and show that
${\mathcal{D}}$
, and show that
 ${\mathcal{D}}E_{2r}^{\ast }(g,s)=E_{2r+2}^{\ast }(g,s)$
. With this identity, Theorem 5.2 for
${\mathcal{D}}E_{2r}^{\ast }(g,s)=E_{2r+2}^{\ast }(g,s)$
. With this identity, Theorem 5.2 for
![]() $r\geqslant 0$
implies the same statement for
$r\geqslant 0$
implies the same statement for
![]() $r+1$
. Here,
$r+1$
. Here,
![]() ${\mathcal{D}}$
is an element of the universal enveloping algebra of the Lie algebra of
${\mathcal{D}}$
is an element of the universal enveloping algebra of the Lie algebra of
![]() $\text{G}(\mathbf{R})$
. To analyze
$\text{G}(\mathbf{R})$
. To analyze
 $E_{0}^{\ast }(g,s)$
, we apply Langlands’ theorem of the constant term and his functional equation [Reference LanglandsLan76]. In order to do the requisite intertwining operator calculations needed to apply these theorems of Langlands, we need some basic results about
$E_{0}^{\ast }(g,s)$
, we apply Langlands’ theorem of the constant term and his functional equation [Reference LanglandsLan76]. In order to do the requisite intertwining operator calculations needed to apply these theorems of Langlands, we need some basic results about
![]() $\text{G}(\mathbf{A})$
, such as a description of the minimal parabolic subgroup and Iwasawa decomposition. We begin with a summary of these results on
$\text{G}(\mathbf{A})$
, such as a description of the minimal parabolic subgroup and Iwasawa decomposition. We begin with a summary of these results on
![]() $\text{G}(\mathbf{A})$
.
$\text{G}(\mathbf{A})$
.
7.1 Minimal parabolic and Iwasawa decomposition
Suppose
![]() $F$
is a field of characteristic zero,
$F$
is a field of characteristic zero,
![]() $B$
is a quaternion algebra over
$B$
is a quaternion algebra over
![]() $F$
,
$F$
,
 $J=H_{3}(B)$
, and
$J=H_{3}(B)$
, and
![]() $\text{G}$
is the reductive
$\text{G}$
is the reductive
![]() $F$
-group that preserves the symplectic and quartic form on
$F$
-group that preserves the symplectic and quartic form on
 $W=F\oplus J\oplus J\oplus F$
, up to similitude. We describe a parabolic subgroup
$W=F\oplus J\oplus J\oplus F$
, up to similitude. We describe a parabolic subgroup
![]() $P_{0}$
of
$P_{0}$
of
![]() $\text{G}$
, which is minimal when
$\text{G}$
, which is minimal when
![]() $B$
is a division algebra, and the corresponding Iwasawa decomposition.
$B$
is a division algebra, and the corresponding Iwasawa decomposition.
For an element
![]() $x$
of
$x$
of
![]() $W$
, denote by
$W$
, denote by
 $a(x),b(x),c(x),d(x)$
the elements of
$a(x),b(x),c(x),d(x)$
the elements of
 $F,J,J,F$
respectively so that
$F,J,J,F$
respectively so that
 $x=(a(x),b(x),c(x),d(x)).$
If
$x=(a(x),b(x),c(x),d(x)).$
If
![]() $b$
is in
$b$
is in
 $H_{3}(B)\subseteq M_{3}(B)$
, we denote
$H_{3}(B)\subseteq M_{3}(B)$
, we denote
![]() $b_{ij}$
the element of
$b_{ij}$
the element of
![]() $B$
in the
$B$
in the
![]() $i,j$
position of
$i,j$
position of
![]() $b$
. We denote by
$b$
. We denote by
![]() $e_{ij}$
the element of
$e_{ij}$
the element of
![]() $M_{3}(B)$
that is
$M_{3}(B)$
that is
![]() $1$
at the
$1$
at the
![]() $i,j$
position and zero elsewhere.
$i,j$
position and zero elsewhere.
Denote by
![]() $S_{4}$
the subspace of
$S_{4}$
the subspace of
![]() $W$
consisting of
$W$
consisting of
 $(a,b,c,d)$
with
$(a,b,c,d)$
with
![]() $a=0$
,
$a=0$
,
![]() $b_{ij}=0$
unless
$b_{ij}=0$
unless
![]() $i,j=1$
,
$i,j=1$
,
 $c_{1k}=c_{j1}=0$
for all
$c_{1k}=c_{j1}=0$
for all
![]() $j,k$
. Then
$j,k$
. Then
![]() $S_{4}$
is an eight-dimensional isotropic subspace of
$S_{4}$
is an eight-dimensional isotropic subspace of
![]() $W$
. Furthermore, every element
$W$
. Furthermore, every element
![]() $s\in S_{4}$
has rank at most two. Inside of
$s\in S_{4}$
has rank at most two. Inside of
![]() $S_{4}$
we consider the two-dimensional subspace
$S_{4}$
we consider the two-dimensional subspace
![]() $S_{2}$
spanned by
$S_{2}$
spanned by
 $(0,0,e_{33},0)$
and
$(0,0,e_{33},0)$
and
 $(0,0,0,1)$
. Then every element of
$(0,0,0,1)$
. Then every element of
![]() $S_{2}$
has rank at most one. Finally, inside of
$S_{2}$
has rank at most one. Finally, inside of
![]() $S_{2}$
we consider the line
$S_{2}$
we consider the line
 $S_{1}=F(0,0,0,1)$
. (The reasoning for the numbering will become apparent shortly.) Set
$S_{1}=F(0,0,0,1)$
. (The reasoning for the numbering will become apparent shortly.) Set
![]() ${\mathcal{F}}_{0}$
to be the flag
${\mathcal{F}}_{0}$
to be the flag
 $S_{4}\supseteq S_{2}\supseteq S_{1}$
, and define
$S_{4}\supseteq S_{2}\supseteq S_{1}$
, and define
![]() $P_{0}$
to be the subgroup of
$P_{0}$
to be the subgroup of
![]() $\text{G}$
stabilizing
$\text{G}$
stabilizing
![]() ${\mathcal{F}}_{0}$
. Now, define
${\mathcal{F}}_{0}$
. Now, define
![]() $S_{3}$
to be the seven-dimensional space in
$S_{3}$
to be the seven-dimensional space in
![]() $S_{4}$
consisting of the
$S_{4}$
consisting of the
 $x=(0,b,c,d)$
with
$x=(0,b,c,d)$
with
![]() $b=0$
, i.e.,
$b=0$
, i.e.,
 $S_{3}=S_{4}\cap (0,0,\ast ,\ast )$
. It can be shown that since
$S_{3}=S_{4}\cap (0,0,\ast ,\ast )$
. It can be shown that since
![]() $P_{0}$
stabilizes
$P_{0}$
stabilizes
 $(0,0,0,\ast )$
, it automatically stabilizes
$(0,0,0,\ast )$
, it automatically stabilizes
 $(0,0,\ast ,\ast )$
, and thus
$(0,0,\ast ,\ast )$
, and thus
![]() $P_{0}$
stabilizes
$P_{0}$
stabilizes
![]() $S_{3}$
.
$S_{3}$
.
Proposition 7.1. The subgroup
![]() $P_{0}$
is a parabolic subgroup of
$P_{0}$
is a parabolic subgroup of
![]() $\text{G}$
. Denote by
$\text{G}$
. Denote by
![]() $T$
the diagonal maximal torus in
$T$
the diagonal maximal torus in
![]() $\operatorname{GSp}_{6}$
, considered inside of
$\operatorname{GSp}_{6}$
, considered inside of
![]() $\text{G}$
. If
$\text{G}$
. If
![]() $B$
is not split over
$B$
is not split over
![]() $F$
, then
$F$
, then
![]() $T$
is a maximal split torus of
$T$
is a maximal split torus of
![]() $\text{G}$
,
$\text{G}$
,
![]() $P_{0}$
is a minimal parabolic subgroup, and
$P_{0}$
is a minimal parabolic subgroup, and
![]() $\text{G}$
has rational root type
$\text{G}$
has rational root type
![]() $C_{3}$
.
$C_{3}$
.
Now suppose
![]() $F=\mathbf{Q}$
, and
$F=\mathbf{Q}$
, and
![]() $B_{\mathbf{R}}$
is a division algebra. We describe the associated Iwasawa decomposition of
$B_{\mathbf{R}}$
is a division algebra. We describe the associated Iwasawa decomposition of
![]() $\text{G}(\mathbf{A})$
. Define
$\text{G}(\mathbf{A})$
. Define
![]() $K_{p}$
to be the subgroup of
$K_{p}$
to be the subgroup of
![]() $\text{G}(\mathbf{Q}_{p})$
that acts invertibly on the lattice
$\text{G}(\mathbf{Q}_{p})$
that acts invertibly on the lattice
![]() $W(\mathbf{Z}_{p})$
. Define
$W(\mathbf{Z}_{p})$
. Define
![]() $K_{\infty }$
to be the subgroup of
$K_{\infty }$
to be the subgroup of
 $\text{G}^{1,+}(\mathbf{R})$
that commutes with
$\text{G}^{1,+}(\mathbf{R})$
that commutes with
![]() $J$
. Here
$J$
. Here
![]() $\text{G}^{1}$
denotes the elements of
$\text{G}^{1}$
denotes the elements of
![]() $\text{G}$
with similitude equal to 1. Because
$\text{G}$
with similitude equal to 1. Because
 $(v,w):=\langle v,wJ\rangle$
is an inner product on
$(v,w):=\langle v,wJ\rangle$
is an inner product on
![]() $W(\mathbf{R})$
,
$W(\mathbf{R})$
,
![]() $K_{\infty }$
is compact.
$K_{\infty }$
is compact.
Proposition 7.2. The subgroup
![]() $K_{\infty }$
is the stabilizer of
$K_{\infty }$
is the stabilizer of
![]() $i$
for the
$i$
for the
 $\text{G}^{1,+}(\mathbf{R})$
action on the Hermitian symmetric space
$\text{G}^{1,+}(\mathbf{R})$
action on the Hermitian symmetric space
![]() ${\mathcal{H}}$
. For all places
${\mathcal{H}}$
. For all places
![]() $v$
of
$v$
of
![]() $\mathbf{Q}$
, one has the decomposition
$\mathbf{Q}$
, one has the decomposition
 $\text{G}(\mathbf{Q}_{v})=P_{0}(\mathbf{Q}_{v})K_{v}$
.
$\text{G}(\mathbf{Q}_{v})=P_{0}(\mathbf{Q}_{v})K_{v}$
.
We omit the proofs of Propositions 7.1 and 7.2, as they appear to be well known.
7.2 The spherical Eisenstein series
We are now ready to analyze the spherical normalized Eisenstein series. Recall we denote by
![]() $P$
the parabolic subgroup of
$P$
the parabolic subgroup of
![]() $\text{G}$
that is the stabilizer of the line spanned by
$\text{G}$
that is the stabilizer of the line spanned by
 $f=(0,0,0,1)$
. If
$f=(0,0,0,1)$
. If
![]() $p\in P$
, then
$p\in P$
, then
![]() $p$
acts on this line as multiplication by some
$p$
acts on this line as multiplication by some
![]() $d$
in
$d$
in
![]() $\operatorname{GL}_{1}$
, and acts on the one-dimensional space
$\operatorname{GL}_{1}$
, and acts on the one-dimensional space
 $W/(f)^{\bot }$
as multiplication by some
$W/(f)^{\bot }$
as multiplication by some
![]() $a$
in
$a$
in
![]() $\operatorname{GL}_{1}$
. Define a character
$\operatorname{GL}_{1}$
. Define a character
 $\unicode[STIX]{x1D712}_{s}:P(\mathbf{A})\rightarrow \mathbf{C}^{\times }$
as
$\unicode[STIX]{x1D712}_{s}:P(\mathbf{A})\rightarrow \mathbf{C}^{\times }$
as
 $\unicode[STIX]{x1D712}_{s}(p)=|a/d|^{s}$
. For every place
$\unicode[STIX]{x1D712}_{s}(p)=|a/d|^{s}$
. For every place
![]() $v$
of
$v$
of
![]() $\mathbf{Q}$
, set
$\mathbf{Q}$
, set
![]() $f_{v}(g,s)$
to be the unique element in
$f_{v}(g,s)$
to be the unique element in
 $\text{Ind}_{P(\mathbf{Q}_{v})}^{\text{G}(\mathbf{Q}_{v})}(\unicode[STIX]{x1D712}_{s})$
that is
$\text{Ind}_{P(\mathbf{Q}_{v})}^{\text{G}(\mathbf{Q}_{v})}(\unicode[STIX]{x1D712}_{s})$
that is
![]() $1$
on
$1$
on
![]() $K_{v}$
. The unnormalized spherical Eisenstein series is
$K_{v}$
. The unnormalized spherical Eisenstein series is
 $$\begin{eqnarray}E_{0}(g,s)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})}f(\unicode[STIX]{x1D6FE}g,s),\end{eqnarray}$$
$$\begin{eqnarray}E_{0}(g,s)=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash \text{G}(\mathbf{Q})}f(\unicode[STIX]{x1D6FE}g,s),\end{eqnarray}$$
where
 $f(g,s)=\prod _{\text{all}~v}f_{v}(g_{v},s)$
and the sum converges for
$f(g,s)=\prod _{\text{all}~v}f_{v}(g_{v},s)$
and the sum converges for
 $\text{Re}(s)\gg 0$
. The normalized Eisenstein series
$\text{Re}(s)\gg 0$
. The normalized Eisenstein series
 $E_{0}^{\ast }(g,s)$
is
$E_{0}^{\ast }(g,s)$
is
 $$\begin{eqnarray}\displaystyle E_{0}^{\ast }(g,s) & = & \displaystyle D_{B}^{s}\biggl(\mathop{\prod }_{v<\infty ~\text{split}}\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-2)\unicode[STIX]{x1D701}_{v}(2s-4)\biggr)\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-4)\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{0}^{\ast }(g,s) & = & \displaystyle D_{B}^{s}\biggl(\mathop{\prod }_{v<\infty ~\text{split}}\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-2)\unicode[STIX]{x1D701}_{v}(2s-4)\biggr)\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-4)\biggr)\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-8)E_{0}(g,s).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \times \,\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-8)E_{0}(g,s).\end{eqnarray}$$
Here
 $D_{B}=\prod _{p<\infty ~\text{ramified}}p$
is the product of the finite primes
$D_{B}=\prod _{p<\infty ~\text{ramified}}p$
is the product of the finite primes
![]() $p$
for which
$p$
for which
 $B\otimes \mathbf{Q}_{p}$
is not split. By the theory of Langlands,
$B\otimes \mathbf{Q}_{p}$
is not split. By the theory of Langlands,
![]() $E_{0}^{\ast }$
has meromorphic continuation in
$E_{0}^{\ast }$
has meromorphic continuation in
![]() $s$
and is a function of moderate growth where it is finite. The purpose of this section is to describe the proof of the following theorem.
$s$
and is a function of moderate growth where it is finite. The purpose of this section is to describe the proof of the following theorem.
Theorem 7.3. The Eisenstein series
 $E_{0}^{\ast }(g,s)$
has at most finitely many poles, all contained in the set of integer and half-integer points in the interval
$E_{0}^{\ast }(g,s)$
has at most finitely many poles, all contained in the set of integer and half-integer points in the interval
![]() $[0,5]$
, and satisfies the functional equation
$[0,5]$
, and satisfies the functional equation
 $E_{0}^{\ast }(g,s)=E_{0}^{\ast }(g,5-s)$
.
$E_{0}^{\ast }(g,s)=E_{0}^{\ast }(g,5-s)$
.
The proof will be an application of Langlands’ theory of the constant term, and the Langlands’ functional equation. We begin with the computation of intertwining operators on
 $\operatorname{GL}_{2}(B)$
.
$\operatorname{GL}_{2}(B)$
.
For a finite prime
![]() $p$
, set
$p$
, set
 $K_{p}^{B}\subseteq \operatorname{GL}_{2}(B_{p})$
to be the subgroup acting invertibly on the lattice
$K_{p}^{B}\subseteq \operatorname{GL}_{2}(B_{p})$
to be the subgroup acting invertibly on the lattice
 $B_{0}(\mathbf{Z}_{p})\oplus B_{0}(\mathbf{Z}_{p})$
. Define
$B_{0}(\mathbf{Z}_{p})\oplus B_{0}(\mathbf{Z}_{p})$
. Define
![]() $K_{\infty }^{B}$
to be the subgroup of
$K_{\infty }^{B}$
to be the subgroup of
 $\operatorname{GL}_{2}(B_{\infty })$
consisting of those
$\operatorname{GL}_{2}(B_{\infty })$
consisting of those
 $m\in \operatorname{GL}_{2}(B_{\infty })$
with
$m\in \operatorname{GL}_{2}(B_{\infty })$
with
 $mm^{\ast }=1$
. Consider the function
$mm^{\ast }=1$
. Consider the function
 $f_{v}^{B}(g,s_{1},s_{2}):\operatorname{GL}_{2}(B_{v})\rightarrow \mathbf{C}$
defined by
$f_{v}^{B}(g,s_{1},s_{2}):\operatorname{GL}_{2}(B_{v})\rightarrow \mathbf{C}$
defined by
 $$\begin{eqnarray}f_{v}^{B}((\!\begin{smallmatrix}b_{1} & \ast \\ & b_{2}\end{smallmatrix}\!),s_{1},s_{2})=|n(b_{1})|^{s_{1}+1}|n(b_{2})|^{s_{2}-1}\end{eqnarray}$$
$$\begin{eqnarray}f_{v}^{B}((\!\begin{smallmatrix}b_{1} & \ast \\ & b_{2}\end{smallmatrix}\!),s_{1},s_{2})=|n(b_{1})|^{s_{1}+1}|n(b_{2})|^{s_{2}-1}\end{eqnarray}$$
and
 $f_{v}^{B}(K_{v},s_{1},s_{2})=1$
.
$f_{v}^{B}(K_{v},s_{1},s_{2})=1$
.
Definition 7.4. If
![]() $v<\infty$
, and
$v<\infty$
, and
![]() $B_{v}$
is split, define
$B_{v}$
is split, define
 $\unicode[STIX]{x1D701}_{B_{v}}(s)=\unicode[STIX]{x1D701}_{v}(s)\unicode[STIX]{x1D701}_{v}(s-1)$
. If
$\unicode[STIX]{x1D701}_{B_{v}}(s)=\unicode[STIX]{x1D701}_{v}(s)\unicode[STIX]{x1D701}_{v}(s-1)$
. If
![]() $v<\infty$
and
$v<\infty$
and
![]() $B_{v}$
is ramified, define
$B_{v}$
is ramified, define
 $\unicode[STIX]{x1D701}_{B_{v}}(s)=\unicode[STIX]{x1D701}_{v}(s)$
. If
$\unicode[STIX]{x1D701}_{B_{v}}(s)=\unicode[STIX]{x1D701}_{v}(s)$
. If
![]() $B_{\infty }$
is ramified (as we assume throughout this section), define
$B_{\infty }$
is ramified (as we assume throughout this section), define
 $\unicode[STIX]{x1D701}_{B_{\infty }}(s)=D_{B}^{s/2}\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s)$
.
$\unicode[STIX]{x1D701}_{B_{\infty }}(s)=D_{B}^{s/2}\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s)$
.
Lemma 7.5. For
![]() $x$
in
$x$
in
![]() $B$
, define
$B$
, define
 $\overline{n}(x)\in \operatorname{GL}_{2}(B)$
to be the matrix
$\overline{n}(x)\in \operatorname{GL}_{2}(B)$
to be the matrix
![]() $(\!\begin{smallmatrix}1 & \\ x & 1\end{smallmatrix}\!)$
. Suppose the measure on
$(\!\begin{smallmatrix}1 & \\ x & 1\end{smallmatrix}\!)$
. Suppose the measure on
![]() $B(\mathbf{A})$
is normalized so that
$B(\mathbf{A})$
is normalized so that
 $B(\mathbf{Q})\backslash B(\mathbf{A})$
has measure one, and
$B(\mathbf{Q})\backslash B(\mathbf{A})$
has measure one, and
![]() $B_{0}(\mathbf{Z}_{p})$
has measure one for all finite primes, both split and ramified. Then, if
$B_{0}(\mathbf{Z}_{p})$
has measure one for all finite primes, both split and ramified. Then, if
 $\text{Re}(s_{1}-s_{2})\gg 0$
,
$\text{Re}(s_{1}-s_{2})\gg 0$
,
 $$\begin{eqnarray}\int _{B_{v}}f_{v}^{B}(\overline{n}(x),s_{1},s_{2})\,dx=\frac{\unicode[STIX]{x1D701}_{B_{v}}(s_{1}-s_{2})}{\unicode[STIX]{x1D701}_{B_{v}}(s_{1}-s_{2}+2)}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{B_{v}}f_{v}^{B}(\overline{n}(x),s_{1},s_{2})\,dx=\frac{\unicode[STIX]{x1D701}_{B_{v}}(s_{1}-s_{2})}{\unicode[STIX]{x1D701}_{B_{v}}(s_{1}-s_{2}+2)}.\end{eqnarray}$$
Proof. Write
![]() $e,f$
for the basis of
$e,f$
for the basis of
![]() $B^{2}$
. For a finite prime
$B^{2}$
. For a finite prime
![]() $v$
, define
$v$
, define
![]() $\unicode[STIX]{x1D6F7}_{v}$
on
$\unicode[STIX]{x1D6F7}_{v}$
on
![]() $B_{v}^{2}$
to be the characteristic function of
$B_{v}^{2}$
to be the characteristic function of
 $B_{0}(\mathbf{Z}_{v})^{2}$
. Define
$B_{0}(\mathbf{Z}_{v})^{2}$
. Define
 $\unicode[STIX]{x1D6F7}_{\infty }(b_{1}e+b_{2}f)=e^{-2\unicode[STIX]{x1D70B}(n(b_{1})+n(b_{2}))}$
. Note that, for all
$\unicode[STIX]{x1D6F7}_{\infty }(b_{1}e+b_{2}f)=e^{-2\unicode[STIX]{x1D70B}(n(b_{1})+n(b_{2}))}$
. Note that, for all
![]() $v$
,
$v$
,
 $\unicode[STIX]{x1D6F7}_{v}(b_{1}e+b_{2}f)=\unicode[STIX]{x1D6F7}_{v}(b_{1}e)\unicode[STIX]{x1D6F7}_{v}(b_{2}f)$
, and that
$\unicode[STIX]{x1D6F7}_{v}(b_{1}e+b_{2}f)=\unicode[STIX]{x1D6F7}_{v}(b_{1}e)\unicode[STIX]{x1D6F7}_{v}(b_{2}f)$
, and that
 $\unicode[STIX]{x1D6F7}_{v}(wK_{v})=\unicode[STIX]{x1D6F7}_{v}(w)$
for all
$\unicode[STIX]{x1D6F7}_{v}(wK_{v})=\unicode[STIX]{x1D6F7}_{v}(w)$
for all
![]() $w$
in
$w$
in
![]() $B_{v}^{2}$
. Set
$B_{v}^{2}$
. Set
 $s=s_{1}-s_{2}$
. Consider
$s=s_{1}-s_{2}$
. Consider
 $$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}}(g,s_{1},s_{2})=|\text{det}(gg^{\ast })|^{s_{1}+1}\int _{B_{v}^{\times }}\unicode[STIX]{x1D6F7}_{v}(yfg)|n(y)|^{s+2}\,dy.\end{eqnarray}$$
$$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}}(g,s_{1},s_{2})=|\text{det}(gg^{\ast })|^{s_{1}+1}\int _{B_{v}^{\times }}\unicode[STIX]{x1D6F7}_{v}(yfg)|n(y)|^{s+2}\,dy.\end{eqnarray}$$
Then, the transformation properties of
 $f^{\unicode[STIX]{x1D6F7}}(g,s_{1},s_{2})$
implies the identity
$f^{\unicode[STIX]{x1D6F7}}(g,s_{1},s_{2})$
implies the identity
 $$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}}(g,s_{1},s_{2})=f^{\unicode[STIX]{x1D6F7}}(1,s_{1},s_{2})f_{v}^{B}(g,s_{1},s_{2}).\end{eqnarray}$$
$$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}}(g,s_{1},s_{2})=f^{\unicode[STIX]{x1D6F7}}(1,s_{1},s_{2})f_{v}^{B}(g,s_{1},s_{2}).\end{eqnarray}$$
We compute
 $$\begin{eqnarray}\displaystyle \int _{B_{v}}f^{\unicode[STIX]{x1D6F7}}(\overline{n}(x),s_{1},s_{2})\,dx & = & \displaystyle \int _{B_{v}^{\times }}\int _{B_{v}}\unicode[STIX]{x1D6F7}(y(xe+f))|n(y)|^{s+2}\,dx\,dy\nonumber\\ \displaystyle & = & \displaystyle \int _{B_{v}^{\times }}|n(y)|^{s+2}\unicode[STIX]{x1D6F7}_{v}(yf)\int _{B_{v}}\unicode[STIX]{x1D6F7}_{v}(yxe)\,dx\,dy\nonumber\\ \displaystyle & = & \displaystyle \biggl(\int _{B_{v}^{\times }}|n(y)|^{s}\unicode[STIX]{x1D6F7}_{v}(yf)\,dy\biggr)\biggl(\int _{B_{v}}\unicode[STIX]{x1D6F7}_{v}(xe)\,dx\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{B_{v}}f^{\unicode[STIX]{x1D6F7}}(\overline{n}(x),s_{1},s_{2})\,dx & = & \displaystyle \int _{B_{v}^{\times }}\int _{B_{v}}\unicode[STIX]{x1D6F7}(y(xe+f))|n(y)|^{s+2}\,dx\,dy\nonumber\\ \displaystyle & = & \displaystyle \int _{B_{v}^{\times }}|n(y)|^{s+2}\unicode[STIX]{x1D6F7}_{v}(yf)\int _{B_{v}}\unicode[STIX]{x1D6F7}_{v}(yxe)\,dx\,dy\nonumber\\ \displaystyle & = & \displaystyle \biggl(\int _{B_{v}^{\times }}|n(y)|^{s}\unicode[STIX]{x1D6F7}_{v}(yf)\,dy\biggr)\biggl(\int _{B_{v}}\unicode[STIX]{x1D6F7}_{v}(xe)\,dx\biggr).\nonumber\end{eqnarray}$$
Hence
 $$\begin{eqnarray}\int _{B_{v}}f_{v}^{B}(\overline{n}(x),s_{1},s_{2})\,dx=\frac{(\int _{B_{v}^{\times }}|n(y)|^{s}\unicode[STIX]{x1D6F7}_{v}(yf)\,dy)(\int _{B_{v}}\unicode[STIX]{x1D6F7}_{v}(xe)\,dx)}{(\int _{B_{v}^{\times }}|n(y)|^{s+2}\unicode[STIX]{x1D6F7}_{v}(yf)\,dy)}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{B_{v}}f_{v}^{B}(\overline{n}(x),s_{1},s_{2})\,dx=\frac{(\int _{B_{v}^{\times }}|n(y)|^{s}\unicode[STIX]{x1D6F7}_{v}(yf)\,dy)(\int _{B_{v}}\unicode[STIX]{x1D6F7}_{v}(xe)\,dx)}{(\int _{B_{v}^{\times }}|n(y)|^{s+2}\unicode[STIX]{x1D6F7}_{v}(yf)\,dy)}.\end{eqnarray}$$
When
![]() $v<\infty$
, the first integral in the numerator of this fraction gives
$v<\infty$
, the first integral in the numerator of this fraction gives
![]() $\unicode[STIX]{x1D701}_{B_{v}(s)}$
and the second integral gives 1. When
$\unicode[STIX]{x1D701}_{B_{v}(s)}$
and the second integral gives 1. When
![]() $v=\infty$
, the first integral in the numerator gives
$v=\infty$
, the first integral in the numerator gives
![]() $\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s)$
, up to a nonzero constant. Via Lemma 7.6, the second integral gives
$\unicode[STIX]{x1D6E4}_{\mathbf{C}}(s)$
, up to a nonzero constant. Via Lemma 7.6, the second integral gives
![]() $D_{B}^{-1}$
. The lemma follows.◻
$D_{B}^{-1}$
. The lemma follows.◻
Since
![]() $B_{\mathbf{R}}$
is the Hamilton quaternions, we have
$B_{\mathbf{R}}$
is the Hamilton quaternions, we have
 $B_{\mathbf{R}}=\mathbf{R}\oplus \mathbf{R}i\oplus \mathbf{R}j\oplus \mathbf{R}k$
with
$B_{\mathbf{R}}=\mathbf{R}\oplus \mathbf{R}i\oplus \mathbf{R}j\oplus \mathbf{R}k$
with
 $i^{2}=j^{2}=k^{2}=-1$
, and
$i^{2}=j^{2}=k^{2}=-1$
, and
![]() $ij=k$
.
$ij=k$
.
Lemma 7.6. Suppose
![]() $\unicode[STIX]{x1D707}_{\text{std}}$
is the measure on
$\unicode[STIX]{x1D707}_{\text{std}}$
is the measure on
![]() $B_{\mathbf{R}}$
that gives the box spanned by
$B_{\mathbf{R}}$
that gives the box spanned by
![]() $1,i,j,k$
measure one, and
$1,i,j,k$
measure one, and
![]() $\unicode[STIX]{x1D707}_{\text{norm}}$
is the measure determined by the statement of Lemma 7.5. Then
$\unicode[STIX]{x1D707}_{\text{norm}}$
is the measure determined by the statement of Lemma 7.5. Then
 $\unicode[STIX]{x1D707}_{\text{norm}}=4D_{B}^{-1}\unicode[STIX]{x1D707}_{\text{std}}$
.
$\unicode[STIX]{x1D707}_{\text{norm}}=4D_{B}^{-1}\unicode[STIX]{x1D707}_{\text{std}}$
.
Proof. The normalized measure is characterized by
 $\unicode[STIX]{x1D707}_{\text{norm}}(B_{0}\backslash B_{\mathbf{R}})=1$
. Suppose
$\unicode[STIX]{x1D707}_{\text{norm}}(B_{0}\backslash B_{\mathbf{R}})=1$
. Suppose
![]() $B_{0}$
corresponds to the half-integral symmetric matrix
$B_{0}$
corresponds to the half-integral symmetric matrix
![]() $T$
. Then the covolume of
$T$
. Then the covolume of
![]() $B_{0}$
in
$B_{0}$
in
![]() $B_{\mathbf{R}}$
in
$B_{\mathbf{R}}$
in
![]() $\unicode[STIX]{x1D707}_{\text{std}}$
is
$\unicode[STIX]{x1D707}_{\text{std}}$
is
![]() $\det (T)$
. Hence
$\det (T)$
. Hence
 $\unicode[STIX]{x1D707}_{\text{norm}}=\det (T)^{-1}\unicode[STIX]{x1D707}_{\text{std}}$
. Since
$\unicode[STIX]{x1D707}_{\text{norm}}=\det (T)^{-1}\unicode[STIX]{x1D707}_{\text{std}}$
. Since
 $D_{B}=4\det (T)$
by Corollary 3.4, we are done.◻
$D_{B}=4\det (T)$
by Corollary 3.4, we are done.◻
Denote by
 $M_{0}\subseteq P_{0}$
the centralizer of the maximal split torus
$M_{0}\subseteq P_{0}$
the centralizer of the maximal split torus
![]() $T$
defined in Proposition 7.1. We now describe some characters on
$T$
defined in Proposition 7.1. We now describe some characters on
![]() $M_{0}(\mathbf{A})$
. First, the weight spaces for the action of
$M_{0}(\mathbf{A})$
. First, the weight spaces for the action of
![]() $T$
on
$T$
on
![]() $W$
are exactly the coordinate spaces, i.e., the
$W$
are exactly the coordinate spaces, i.e., the
 $a(v),b_{ij}(v),c_{ij}(v),d(v)$
, with
$a(v),b_{ij}(v),c_{ij}(v),d(v)$
, with
![]() $i\leqslant j$
. Since
$i\leqslant j$
. Since
![]() $T$
acts on these spaces with distinct weights,
$T$
acts on these spaces with distinct weights,
![]() $M_{0}$
is exactly the subgroup of
$M_{0}$
is exactly the subgroup of
![]() $\text{G}$
preserving the coordinate spaces.
$\text{G}$
preserving the coordinate spaces.
Consistent with the notation in (2.2), we write
 $a_{i}(b(v))=b_{i+1,i-1}(v)$
and
$a_{i}(b(v))=b_{i+1,i-1}(v)$
and
 $c_{i}(b(v))=b_{i,i}(v)$
, with the indices in the set
$c_{i}(b(v))=b_{i,i}(v)$
, with the indices in the set
 $\{1,2,3\}$
and taken modulo 3. If
$\{1,2,3\}$
and taken modulo 3. If
 $m\in M_{0}$
, one can verify easily that
$m\in M_{0}$
, one can verify easily that
![]() $m$
preserves the norm on the coordinate spaces
$m$
preserves the norm on the coordinate spaces
 $a_{i}(b(v))$
, up to scaling. For
$a_{i}(b(v))$
, up to scaling. For
 $m\in M_{0}$
, define
$m\in M_{0}$
, define
![]() $m_{i}$
to be the endomorphism of
$m_{i}$
to be the endomorphism of
 $B=a_{i}(\{b(v):v\in W\})$
so that
$B=a_{i}(\{b(v):v\in W\})$
so that
 $a_{i}(b(vm))=\unicode[STIX]{x1D708}(m)(a_{i}(b(v)))m_{i}$
for all
$a_{i}(b(vm))=\unicode[STIX]{x1D708}(m)(a_{i}(b(v)))m_{i}$
for all
![]() $v$
in
$v$
in
![]() $W$
. (In fact, one can show that
$W$
. (In fact, one can show that
![]() $\unicode[STIX]{x1D708}$
and the
$\unicode[STIX]{x1D708}$
and the
![]() $m_{i}$
determine
$m_{i}$
determine
![]() $m$
.) Since
$m$
.) Since
![]() $m_{i}$
preserves the norm on
$m_{i}$
preserves the norm on
![]() $B$
up to scaling, define
$B$
up to scaling, define
![]() $|m_{i}|$
by the equality
$|m_{i}|$
by the equality
 $|n(bm_{i})|=|m_{i}|\,|n(b)|$
,
$|n(bm_{i})|=|m_{i}|\,|n(b)|$
,
![]() $b\in B$
. Similarly, define
$b\in B$
. Similarly, define
![]() $x_{i}(m)$
by the equality
$x_{i}(m)$
by the equality
 $c_{i}(b(vm))=\unicode[STIX]{x1D708}(m)x_{i}(m)c_{i}(b(v))$
. One immediately sees
$c_{i}(b(vm))=\unicode[STIX]{x1D708}(m)x_{i}(m)c_{i}(b(v))$
. One immediately sees
 $|m_{1}|=|x_{2}x_{3}|$
,
$|m_{1}|=|x_{2}x_{3}|$
,
 $|m_{2}|=|x_{1}x_{3}|$
,
$|m_{2}|=|x_{1}x_{3}|$
,
 $|m_{3}|=|x_{1}x_{2}|$
.
$|m_{3}|=|x_{1}x_{2}|$
.
Recall the elements
 $e=(1,0,0,0)$
and
$e=(1,0,0,0)$
and
 $f=(0,0,0,1)$
of
$f=(0,0,0,1)$
of
![]() $W$
. Since
$W$
. Since
![]() $M_{0}$
preserves the quartic form
$M_{0}$
preserves the quartic form
![]() $Q$
up to similitude squared,
$Q$
up to similitude squared,
 $fm=(\unicode[STIX]{x1D708}(m)x_{1}x_{2}x_{3})^{-1}f$
. Since
$fm=(\unicode[STIX]{x1D708}(m)x_{1}x_{2}x_{3})^{-1}f$
. Since
![]() $M_{0}$
preserves the symplectic form up to similitude,
$M_{0}$
preserves the symplectic form up to similitude,
 $em=\unicode[STIX]{x1D708}(m)^{2}x_{1}x_{2}x_{3}e$
. Thus
$em=\unicode[STIX]{x1D708}(m)^{2}x_{1}x_{2}x_{3}e$
. Thus
 $\unicode[STIX]{x1D712}_{s}(m)=|\unicode[STIX]{x1D708}(m)|^{3s}|m_{1}|^{s}|m_{2}|^{s}|m_{3}|^{s}$
. One has the formula
$\unicode[STIX]{x1D712}_{s}(m)=|\unicode[STIX]{x1D708}(m)|^{3s}|m_{1}|^{s}|m_{2}|^{s}|m_{3}|^{s}$
. One has the formula
 $\unicode[STIX]{x1D6FF}_{P_{0}}(m)=|\unicode[STIX]{x1D708}(m)|^{15}|m_{1}|^{9}|m_{2}|^{5}|m_{3}|$
. Set
$\unicode[STIX]{x1D6FF}_{P_{0}}(m)=|\unicode[STIX]{x1D708}(m)|^{15}|m_{1}|^{9}|m_{2}|^{5}|m_{3}|$
. Set
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{s}(m)=|\unicode[STIX]{x1D708}(m)|^{3s-15/2}|m_{1}|^{s-9/2}|m_{2}|^{s-5/2}|m_{3}|^{s-1/2},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{s}(m)=|\unicode[STIX]{x1D708}(m)|^{3s-15/2}|m_{1}|^{s-9/2}|m_{2}|^{s-5/2}|m_{3}|^{s-1/2},\end{eqnarray}$$
so that
 $\unicode[STIX]{x1D712}_{s}(m)=\unicode[STIX]{x1D706}_{s}(m)\unicode[STIX]{x1D6FF}_{P_{0}}^{1/2}(m)$
.
$\unicode[STIX]{x1D712}_{s}(m)=\unicode[STIX]{x1D706}_{s}(m)\unicode[STIX]{x1D6FF}_{P_{0}}^{1/2}(m)$
.
To understand the analytic properties of
 $E_{0}^{\ast }(g,s)$
, it suffices to restrict to
$E_{0}^{\ast }(g,s)$
, it suffices to restrict to
![]() $\text{G}^{1}$
, so from now on we drop the similitudes
$\text{G}^{1}$
, so from now on we drop the similitudes
![]() $\unicode[STIX]{x1D708}$
. From Proposition 7.1,
$\unicode[STIX]{x1D708}$
. From Proposition 7.1,
![]() $\text{G}$
is of type
$\text{G}$
is of type
![]() $C_{3}$
; let us write
$C_{3}$
; let us write
 $\pm u_{i}\pm u_{j},$
$\pm u_{i}\pm u_{j},$
![]() $i\neq j$
,
$i\neq j$
,
![]() $\pm 2u_{i}$
for its root system determined by the unipotent radical of
$\pm 2u_{i}$
for its root system determined by the unipotent radical of
![]() $P_{0}$
. Before proceeding to the intertwining operator calculations, we state one more preliminary fact. Consider the space of characters
$P_{0}$
. Before proceeding to the intertwining operator calculations, we state one more preliminary fact. Consider the space of characters
 $\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
of
$\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
of
![]() $M_{0}(\mathbf{A})$
that factor through the maps
$M_{0}(\mathbf{A})$
that factor through the maps
![]() $|m_{i}|$
; i.e., this is the space of characters consisting exactly of the maps
$|m_{i}|$
; i.e., this is the space of characters consisting exactly of the maps
 $$\begin{eqnarray}m\mapsto |m_{1}|^{s_{1}}|m_{2}|^{s_{2}}|m_{3}|^{s_{3}}\end{eqnarray}$$
$$\begin{eqnarray}m\mapsto |m_{1}|^{s_{1}}|m_{2}|^{s_{2}}|m_{3}|^{s_{3}}\end{eqnarray}$$
for
 $s_{1},s_{2},s_{3}\in \mathbf{C}$
. We write
$s_{1},s_{2},s_{3}\in \mathbf{C}$
. We write
 $s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
for this character. Denote by
$s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
for this character. Denote by
 $\text{W}_{\text{Sp}_{6}}=(\pm 1)^{3}\rtimes S_{3}$
the Weyl group of
$\text{W}_{\text{Sp}_{6}}=(\pm 1)^{3}\rtimes S_{3}$
the Weyl group of
![]() $\operatorname{Sp}_{6}$
, embedded in
$\operatorname{Sp}_{6}$
, embedded in
![]() $\text{G}$
. We identify
$\text{G}$
. We identify
![]() $\text{W}_{\text{Sp}_{6}}$
with the subset of
$\text{W}_{\text{Sp}_{6}}$
with the subset of
![]() $\operatorname{Sp}_{6}$
that preserves the set
$\operatorname{Sp}_{6}$
that preserves the set
 $\{\pm e_{1},\pm e_{2},\pm e_{3},\pm f_{1},\pm f_{2},\pm f_{3}\}$
. Using the action of
$\{\pm e_{1},\pm e_{2},\pm e_{3},\pm f_{1},\pm f_{2},\pm f_{3}\}$
. Using the action of
![]() $\text{W}_{\text{Sp}_{6}}$
on
$\text{W}_{\text{Sp}_{6}}$
on
 $\bigwedge ^{3}(W_{6})$
, one checks easily that
$\bigwedge ^{3}(W_{6})$
, one checks easily that
![]() $\text{W}_{\text{Sp}_{6}}$
preserves
$\text{W}_{\text{Sp}_{6}}$
preserves
 $\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
and acts on it in the usual way; e.g., the transposition (12) in
$\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
and acts on it in the usual way; e.g., the transposition (12) in
![]() $S_{3}$
takes
$S_{3}$
takes
 $s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
to
$s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
to
 $s_{2}u_{1}+s_{1}u_{2}+s_{3}u_{3}$
and the inversion
$s_{2}u_{1}+s_{1}u_{2}+s_{3}u_{3}$
and the inversion
 $(-1,1,1)$
in
$(-1,1,1)$
in
![]() $(\pm 1)^{3}$
takes this character to
$(\pm 1)^{3}$
takes this character to
 $-s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
.
$-s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
.
Restricting characters in
 $\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
to
$\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
to
![]() $T(\mathbf{A})$
and dividing by two gives an identification
$T(\mathbf{A})$
and dividing by two gives an identification
 $$\begin{eqnarray}\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}\rightarrow X_{un}^{\ast }(T(\mathbf{A}))\simeq X^{\ast }(T)\otimes _{\boldsymbol{ Z}}\mathbf{C},\end{eqnarray}$$
$$\begin{eqnarray}\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}\rightarrow X_{un}^{\ast }(T(\mathbf{A}))\simeq X^{\ast }(T)\otimes _{\boldsymbol{ Z}}\mathbf{C},\end{eqnarray}$$
where
 $X_{un}^{\ast }(T(\mathbf{A}))$
denotes the characters on
$X_{un}^{\ast }(T(\mathbf{A}))$
denotes the characters on
![]() $T(\mathbf{A})$
that factor through
$T(\mathbf{A})$
that factor through
![]() $|\cdot |$
. Thus, if
$|\cdot |$
. Thus, if
![]() $\unicode[STIX]{x1D6FC}^{\vee }$
is a coroot for
$\unicode[STIX]{x1D6FC}^{\vee }$
is a coroot for
![]() $\operatorname{Sp}_{6}$
, and
$\operatorname{Sp}_{6}$
, and
![]() $\unicode[STIX]{x1D707}$
is a character of
$\unicode[STIX]{x1D707}$
is a character of
![]() $M_{0}(\mathbf{A})$
in
$M_{0}(\mathbf{A})$
in
 $\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
, we may write
$\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
, we may write
![]() $\langle \unicode[STIX]{x1D6FC}^{\vee },\unicode[STIX]{x1D707}\rangle$
. For example, for the character
$\langle \unicode[STIX]{x1D6FC}^{\vee },\unicode[STIX]{x1D707}\rangle$
. For example, for the character
 $\unicode[STIX]{x1D707}=s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
, and
$\unicode[STIX]{x1D707}=s_{1}u_{1}+s_{2}u_{2}+s_{3}u_{3}$
, and
 $\unicode[STIX]{x1D6FC}^{\vee }=(u_{1}+u_{2})^{\vee }$
,
$\unicode[STIX]{x1D6FC}^{\vee }=(u_{1}+u_{2})^{\vee }$
,
 $\langle \unicode[STIX]{x1D6FC}^{\vee },\unicode[STIX]{x1D707}\rangle =s_{1}+s_{2}$
.
$\langle \unicode[STIX]{x1D6FC}^{\vee },\unicode[STIX]{x1D707}\rangle =s_{1}+s_{2}$
.
Now we describe the constant term and functional equation computations. For the functional equation, set
 $w_{8}\in \text{W}_{\text{Sp}_{6}}$
to be the element represented by
$w_{8}\in \text{W}_{\text{Sp}_{6}}$
to be the element represented by

so that
 $w_{8}(e_{i})=f_{4-i}$
and
$w_{8}(e_{i})=f_{4-i}$
and
 $w_{8}(f_{i})=-e_{4-i}$
. Then for the spherical section
$w_{8}(f_{i})=-e_{4-i}$
. Then for the spherical section
![]() $f(g,s)$
in
$f(g,s)$
in
 $\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D712}_{s})$
, define
$\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D712}_{s})$
, define
 $$\begin{eqnarray}M(f)(g,s)=\int _{U_{P}(\mathbf{A})\cong H_{3}(B)(\mathbf{A})}f(w_{8}^{-1}n(X)g,s)\,dX\end{eqnarray}$$
$$\begin{eqnarray}M(f)(g,s)=\int _{U_{P}(\mathbf{A})\cong H_{3}(B)(\mathbf{A})}f(w_{8}^{-1}n(X)g,s)\,dX\end{eqnarray}$$
for
![]() $\text{Re}(s)$
sufficiently large. The measure is normalized so that every closed connected subgroup
$\text{Re}(s)$
sufficiently large. The measure is normalized so that every closed connected subgroup
![]() $N$
of
$N$
of
![]() $U_{0}$
has
$U_{0}$
has
 $N(\mathbf{Q})\backslash N(\mathbf{A})$
given measure one. Then
$N(\mathbf{Q})\backslash N(\mathbf{A})$
given measure one. Then
![]() $M(f)$
is a spherical section in
$M(f)$
is a spherical section in
 $\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D712}_{5-s})$
. Indeed,
$\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D712}_{5-s})$
. Indeed,
![]() $w_{8}$
is the Weyl group element taking
$w_{8}$
is the Weyl group element taking
 $u_{1}\mapsto -u_{3}$
,
$u_{1}\mapsto -u_{3}$
,
 $u_{2}\mapsto -u_{2}$
,
$u_{2}\mapsto -u_{2}$
,
 $u_{3}\mapsto -u_{1}$
, and thus that
$u_{3}\mapsto -u_{1}$
, and thus that
![]() $M(f)$
is in
$M(f)$
is in
 $\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D712}_{5-s})$
follows immediately from the computation of
$\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D712}_{5-s})$
follows immediately from the computation of
![]() $\unicode[STIX]{x1D6FF}_{P_{0}}$
above. That
$\unicode[STIX]{x1D6FF}_{P_{0}}$
above. That
![]() $M(f)$
is spherical of course follows from the Iwasawa decomposition. Hence
$M(f)$
is spherical of course follows from the Iwasawa decomposition. Hence
![]() $M(f_{s})$
is equal to
$M(f_{s})$
is equal to
 $c(s)f(g,5-s)$
for some function
$c(s)f(g,5-s)$
for some function
![]() $c(s)$
. Langlands’ functional equation of the Eisenstein series is
$c(s)$
. Langlands’ functional equation of the Eisenstein series is
 $E_{0}^{\ast }(g,f_{s})=E_{0}^{\ast }(g,M(f_{s}))$
. We will determine
$E_{0}^{\ast }(g,f_{s})=E_{0}^{\ast }(g,M(f_{s}))$
. We will determine
![]() $c(s)$
shortly, and then use this to check the functional equation stated in Theorem 7.3.
$c(s)$
shortly, and then use this to check the functional equation stated in Theorem 7.3.
Now for the constant term of the Eisenstein series. We must compute
 $$\begin{eqnarray}E_{0}^{\ast ,P_{0}}(g,s):=\int _{U_{0}(\mathbf{Q})\backslash U_{0}(\mathbf{A})}E_{0}^{\ast }(ug,s)\,du.\end{eqnarray}$$
$$\begin{eqnarray}E_{0}^{\ast ,P_{0}}(g,s):=\int _{U_{0}(\mathbf{Q})\backslash U_{0}(\mathbf{A})}E_{0}^{\ast }(ug,s)\,du.\end{eqnarray}$$
Langlands’ theory of the constant term says that the Eisenstein series has analytic continuation to the same region as that of the constant term. For a character
![]() $\unicode[STIX]{x1D712}$
in
$\unicode[STIX]{x1D712}$
in
 $\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
, denote by
$\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
, denote by
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D712}}^{\text{G}}$
the unique spherical element of
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D712}}^{\text{G}}$
the unique spherical element of
 $\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D6FF}_{P_{0}}^{1/2}\unicode[STIX]{x1D712})$
. For
$\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D6FF}_{P_{0}}^{1/2}\unicode[STIX]{x1D712})$
. For
 $w\in \text{W}_{\text{Sp}_{6}}$
, set
$w\in \text{W}_{\text{Sp}_{6}}$
, set
 $$\begin{eqnarray}A(w,\unicode[STIX]{x1D712})(g):=\int _{N_{w}(\mathbf{A})}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D712}}^{\text{G}}(w^{-1}ng)\,dn\end{eqnarray}$$
$$\begin{eqnarray}A(w,\unicode[STIX]{x1D712})(g):=\int _{N_{w}(\mathbf{A})}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D712}}^{\text{G}}(w^{-1}ng)\,dn\end{eqnarray}$$
when it is absolutely convergent. Here
![]() $N_{w}$
is the group
$N_{w}$
is the group
 $\prod _{\unicode[STIX]{x1D6FC}>0,w^{-1}(\unicode[STIX]{x1D6FC})<0}U_{\unicode[STIX]{x1D6FC}}$
, and
$\prod _{\unicode[STIX]{x1D6FC}>0,w^{-1}(\unicode[STIX]{x1D6FC})<0}U_{\unicode[STIX]{x1D6FC}}$
, and
![]() $U_{\unicode[STIX]{x1D6FC}}$
is the root group in
$U_{\unicode[STIX]{x1D6FC}}$
is the root group in
![]() $\text{G}$
corresponding to the root
$\text{G}$
corresponding to the root
![]() $\unicode[STIX]{x1D6FC}$
. Then
$\unicode[STIX]{x1D6FC}$
. Then
 $A(w,\unicode[STIX]{x1D712})(g)$
is in
$A(w,\unicode[STIX]{x1D712})(g)$
is in
 $\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D6FF}_{P_{0}}^{1/2}w(\unicode[STIX]{x1D712}))$
, and is equal to
$\text{Ind}_{P_{0}(\mathbf{A})}^{\text{G}(\mathbf{A})}(\unicode[STIX]{x1D6FF}_{P_{0}}^{1/2}w(\unicode[STIX]{x1D712}))$
, and is equal to
 $c_{w}(\unicode[STIX]{x1D712})\unicode[STIX]{x1D6F7}_{w(\unicode[STIX]{x1D712})}^{\text{G}}$
for a certain factorizable function
$c_{w}(\unicode[STIX]{x1D712})\unicode[STIX]{x1D6F7}_{w(\unicode[STIX]{x1D712})}^{\text{G}}$
for a certain factorizable function
 $c_{w}=\prod _{v}c_{w}^{v}$
on
$c_{w}=\prod _{v}c_{w}^{v}$
on
 $\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
. By the usual argument [Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, (5.6)], one has
$\text{Char}(M_{0}(\mathbf{A}))^{|\cdot |}$
. By the usual argument [Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, (5.6)], one has
 $$\begin{eqnarray}E_{0}^{P_{0}}(g,s)=\mathop{\sum }_{w\in \unicode[STIX]{x1D6FA}}c_{w}(\unicode[STIX]{x1D706}_{s})\unicode[STIX]{x1D6F7}_{w(\unicode[STIX]{x1D706}_{s})}^{\text{G}}(g),\end{eqnarray}$$
$$\begin{eqnarray}E_{0}^{P_{0}}(g,s)=\mathop{\sum }_{w\in \unicode[STIX]{x1D6FA}}c_{w}(\unicode[STIX]{x1D706}_{s})\unicode[STIX]{x1D6F7}_{w(\unicode[STIX]{x1D706}_{s})}^{\text{G}}(g),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FA}$
is a set of representatives in
$\unicode[STIX]{x1D6FA}$
is a set of representatives in
![]() $\text{W}_{\text{Sp}_{6}}$
for the double coset
$\text{W}_{\text{Sp}_{6}}$
for the double coset
 $P_{0}(\mathbf{Q})\backslash \text{G}(\mathbf{Q})/P(\mathbf{Q})$
.
$P_{0}(\mathbf{Q})\backslash \text{G}(\mathbf{Q})/P(\mathbf{Q})$
.
This double coset has eight elements. The eight Weyl group elements
![]() $w_{i}\in \unicode[STIX]{x1D6FA}$
can be obtained from [Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, Lemma 5.1]. They are indexed by the sets
$w_{i}\in \unicode[STIX]{x1D6FA}$
can be obtained from [Reference Gelbart, Piatetski-Shapiro and RallisGPSR87, Lemma 5.1]. They are indexed by the sets
![]() $S_{i}$
of negative roots
$S_{i}$
of negative roots
![]() $\unicode[STIX]{x1D6FD}$
for which
$\unicode[STIX]{x1D6FD}$
for which
![]() $w_{i}(\unicode[STIX]{x1D6FD})$
is positive. The sets are:
$w_{i}(\unicode[STIX]{x1D6FD})$
is positive. The sets are:
-
(i)
 $S_{1}=\varnothing$
;
$S_{1}=\varnothing$
;
 $c_{1}^{v}(s)=1$
;
$c_{1}^{v}(s)=1$
; -
(ii)
 $S_{2}=\{-2u_{3}\}$
;
$S_{2}=\{-2u_{3}\}$
;
 $c_{2}^{v}(s)=\unicode[STIX]{x1D701}_{v}(2s-1)/\unicode[STIX]{x1D701}_{v}(2s)$
;
$c_{2}^{v}(s)=\unicode[STIX]{x1D701}_{v}(2s-1)/\unicode[STIX]{x1D701}_{v}(2s)$
; -
(iii)
 $S_{3}=S_{2}\cup \{-(u_{2}+u_{3})\}$
;
$S_{3}=S_{2}\cup \{-(u_{2}+u_{3})\}$
;
 $c_{3}^{v}(s)=c_{2}^{v}(s)(\unicode[STIX]{x1D701}_{B_{v}}(2s-3)/\unicode[STIX]{x1D701}_{B_{v}}(2s-1))$
;
$c_{3}^{v}(s)=c_{2}^{v}(s)(\unicode[STIX]{x1D701}_{B_{v}}(2s-3)/\unicode[STIX]{x1D701}_{B_{v}}(2s-1))$
; -
(iv)
 $S_{4}=S_{3}\cup \{-2u_{2}\}$
;
$S_{4}=S_{3}\cup \{-2u_{2}\}$
;
 $c_{4}^{v}(s)=c_{3}^{v}(s)(\unicode[STIX]{x1D701}_{v}(2s-5)/\unicode[STIX]{x1D701}_{v}(2s-4))$
;
$c_{4}^{v}(s)=c_{3}^{v}(s)(\unicode[STIX]{x1D701}_{v}(2s-5)/\unicode[STIX]{x1D701}_{v}(2s-4))$
; -
(v)
 $S_{5}=S_{3}\cup \{-(u_{1}+u_{3})\}$
;
$S_{5}=S_{3}\cup \{-(u_{1}+u_{3})\}$
;
 $c_{5}^{v}(s)=c_{3}^{v}(s)(\unicode[STIX]{x1D701}_{B_{v}}(2s-5)/\unicode[STIX]{x1D701}_{B_{v}}(2s-3))$
;
$c_{5}^{v}(s)=c_{3}^{v}(s)(\unicode[STIX]{x1D701}_{B_{v}}(2s-5)/\unicode[STIX]{x1D701}_{B_{v}}(2s-3))$
; -
(vi)
 $S_{6}=S_{5}\cup \{-2u_{2}\}$
;
$S_{6}=S_{5}\cup \{-2u_{2}\}$
;
 $c_{6}^{v}(s)=c_{5}^{v}(s)(\unicode[STIX]{x1D701}_{v}(2s-5)/\unicode[STIX]{x1D701}_{v}(2s-4))$
;
$c_{6}^{v}(s)=c_{5}^{v}(s)(\unicode[STIX]{x1D701}_{v}(2s-5)/\unicode[STIX]{x1D701}_{v}(2s-4))$
; -
(vii)
 $S_{7}=S_{6}\cup \{-(u_{1}+u_{2})\}$
;
$S_{7}=S_{6}\cup \{-(u_{1}+u_{2})\}$
;
 $c_{7}^{v}(s)=c_{6}^{v}(s)(\unicode[STIX]{x1D701}_{B_{v}}(2s-7)/\unicode[STIX]{x1D701}_{B_{v}}(2s-5))$
;
$c_{7}^{v}(s)=c_{6}^{v}(s)(\unicode[STIX]{x1D701}_{B_{v}}(2s-7)/\unicode[STIX]{x1D701}_{B_{v}}(2s-5))$
; -
(viii)
 $S_{8}=S_{7}\cup \{-2u_{1}\}=\overline{U_{P}}$
;
$S_{8}=S_{7}\cup \{-2u_{1}\}=\overline{U_{P}}$
;
 $c_{v}(s)=c_{8}^{v}(s)=c_{7}^{v}(s)(\unicode[STIX]{x1D701}_{v}(2s-9)/\unicode[STIX]{x1D701}_{v}(2s-8))$
.
$c_{v}(s)=c_{8}^{v}(s)=c_{7}^{v}(s)(\unicode[STIX]{x1D701}_{v}(2s-9)/\unicode[STIX]{x1D701}_{v}(2s-8))$
.
We have also listed the functions
 $c_{i}^{v}(s):=c_{w_{i}}^{v}(\unicode[STIX]{x1D706}_{s})$
. Here, for
$c_{i}^{v}(s):=c_{w_{i}}^{v}(\unicode[STIX]{x1D706}_{s})$
. Here, for
![]() $v=\infty$
,
$v=\infty$
,
![]() $\unicode[STIX]{x1D701}_{v}(s)$
means
$\unicode[STIX]{x1D701}_{v}(s)$
means
![]() $\unicode[STIX]{x1D6E4}_{\mathbf{R}}(s)$
. The computation of the functions
$\unicode[STIX]{x1D6E4}_{\mathbf{R}}(s)$
. The computation of the functions
![]() $c_{i}(s)$
proceeds by the usual Gindikin–Karpelevich argument of factorization of intertwining operators and reduction to rational rank one. Recall that if the length of
$c_{i}(s)$
proceeds by the usual Gindikin–Karpelevich argument of factorization of intertwining operators and reduction to rational rank one. Recall that if the length of
 $w\in \text{W}_{\text{Sp}_{6}}$
is
$w\in \text{W}_{\text{Sp}_{6}}$
is
![]() $r$
, and
$r$
, and
 $w=s_{1}s_{2}\cdots s_{r}$
is an expression of
$w=s_{1}s_{2}\cdots s_{r}$
is an expression of
![]() $w$
as a product of
$w$
as a product of
![]() $r$
reflections,
$r$
reflections,
![]() $s_{i}$
the reflection in the simple root
$s_{i}$
the reflection in the simple root
![]() $\unicode[STIX]{x1D6FC}_{i}$
, then
$\unicode[STIX]{x1D6FC}_{i}$
, then
 $$\begin{eqnarray}c(w,\unicode[STIX]{x1D712})=\mathop{\prod }_{k=1}^{r}\biggl(\int _{U_{\unicode[STIX]{x1D6FC}_{k}}(\mathbf{A})}\unicode[STIX]{x1D6F7}_{s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D712})}^{\text{G}}(s_{k}^{-1}n)\,dn\biggr).\end{eqnarray}$$
$$\begin{eqnarray}c(w,\unicode[STIX]{x1D712})=\mathop{\prod }_{k=1}^{r}\biggl(\int _{U_{\unicode[STIX]{x1D6FC}_{k}}(\mathbf{A})}\unicode[STIX]{x1D6F7}_{s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D712})}^{\text{G}}(s_{k}^{-1}n)\,dn\biggr).\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D6FC}$
is a short simple root, then the root groups
$\unicode[STIX]{x1D6FC}$
is a short simple root, then the root groups
![]() $U_{\unicode[STIX]{x1D6FC}}$
and
$U_{\unicode[STIX]{x1D6FC}}$
and
![]() $U_{-\unicode[STIX]{x1D6FC}}$
sit inside a
$U_{-\unicode[STIX]{x1D6FC}}$
sit inside a
 $\operatorname{GL}_{2}(B)/\unicode[STIX]{x1D707}_{2}$
in
$\operatorname{GL}_{2}(B)/\unicode[STIX]{x1D707}_{2}$
in
![]() $\text{G}$
, that acts on
$\text{G}$
, that acts on
![]() $W$
via the maps
$W$
via the maps
![]() $m(t)$
of § 2. Now, one checks that if
$m(t)$
of § 2. Now, one checks that if
![]() $K_{v}^{B}$
is the compact subgroup of
$K_{v}^{B}$
is the compact subgroup of
 $\operatorname{GL}_{2}(B_{v})$
defined above Lemma 7.5, then
$\operatorname{GL}_{2}(B_{v})$
defined above Lemma 7.5, then
![]() $K_{v}^{B}/\unicode[STIX]{x1D707}_{2}$
sits inside
$K_{v}^{B}/\unicode[STIX]{x1D707}_{2}$
sits inside
![]() $K_{v}$
, for both of these short simple roots, and for all places
$K_{v}$
, for both of these short simple roots, and for all places
![]() $v$
of
$v$
of
![]() $\mathbf{Q}$
. It thus follows from Lemma 7.5 that if
$\mathbf{Q}$
. It thus follows from Lemma 7.5 that if
![]() $\unicode[STIX]{x1D6FC}_{k}$
is a short simple root,
$\unicode[STIX]{x1D6FC}_{k}$
is a short simple root,
 $$\begin{eqnarray}\int _{U_{\unicode[STIX]{x1D6FC}_{k}}(\mathbf{Q}_{v})}\unicode[STIX]{x1D6F7}_{s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D706}_{s})}^{\text{G}}(s_{k}^{-1}n)\,dn=\frac{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FC}_{k}^{\vee },s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D706}_{s})\rangle )}{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FC}_{k}^{\vee },s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D712})\rangle +2)}=\frac{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle )}{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle +2)}\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{\unicode[STIX]{x1D6FC}_{k}}(\mathbf{Q}_{v})}\unicode[STIX]{x1D6F7}_{s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D706}_{s})}^{\text{G}}(s_{k}^{-1}n)\,dn=\frac{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FC}_{k}^{\vee },s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D706}_{s})\rangle )}{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FC}_{k}^{\vee },s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D712})\rangle +2)}=\frac{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle )}{\unicode[STIX]{x1D701}_{B_{v}}(\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle +2)}\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FD}_{k}=s_{r}\cdots s_{k+1}(\unicode[STIX]{x1D6FC}_{k})$
.
$\unicode[STIX]{x1D6FD}_{k}=s_{r}\cdots s_{k+1}(\unicode[STIX]{x1D6FC}_{k})$
.
If
![]() $\unicode[STIX]{x1D6FC}_{k}$
is long root, the analogous formula is
$\unicode[STIX]{x1D6FC}_{k}$
is long root, the analogous formula is
 $$\begin{eqnarray}\int _{U_{\unicode[STIX]{x1D6FC}_{k}}(\mathbf{Q}_{v})}\unicode[STIX]{x1D6F7}_{s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D706}_{s})}^{\text{G}}(s_{k}^{-1}n)\,dn=\frac{\unicode[STIX]{x1D701}_{v}(2\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle )}{\unicode[STIX]{x1D701}_{v}(2\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle +1)}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{\unicode[STIX]{x1D6FC}_{k}}(\mathbf{Q}_{v})}\unicode[STIX]{x1D6F7}_{s_{k+1}\cdots s_{r}(\unicode[STIX]{x1D706}_{s})}^{\text{G}}(s_{k}^{-1}n)\,dn=\frac{\unicode[STIX]{x1D701}_{v}(2\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle )}{\unicode[STIX]{x1D701}_{v}(2\langle \unicode[STIX]{x1D6FD}_{k}^{\vee },\unicode[STIX]{x1D706}_{s}\rangle +1)}.\end{eqnarray}$$
This formula is even easier to establish, because the long root subgroups sit inside
![]() $\operatorname{Sp}_{6}$
, so the computation may done in an
$\operatorname{Sp}_{6}$
, so the computation may done in an
![]() $\operatorname{SL}_{2}$
sitting inside
$\operatorname{SL}_{2}$
sitting inside
![]() $\operatorname{Sp}_{6}$
.
$\operatorname{Sp}_{6}$
.
For
 $w=s_{1}\cdots s_{r}$
, the roots
$w=s_{1}\cdots s_{r}$
, the roots
![]() $-\unicode[STIX]{x1D6FD}_{k}$
are exactly the negative roots
$-\unicode[STIX]{x1D6FD}_{k}$
are exactly the negative roots
![]() $\unicode[STIX]{x1D6FD}$
for which
$\unicode[STIX]{x1D6FD}$
for which
 $w(\unicode[STIX]{x1D6FD})>0$
. The computation of the
$w(\unicode[STIX]{x1D6FD})>0$
. The computation of the
![]() $c_{i}^{v}(s)$
above now follows. Putting in the normalization from (7.1), one now checks without much effort that the constant term of the normalized Eisenstein series
$c_{i}^{v}(s)$
above now follows. Putting in the normalization from (7.1), one now checks without much effort that the constant term of the normalized Eisenstein series
 $E_{0}^{\ast }(g,s)$
has at worst finitely many poles, and they all occur at the integral and half-integral points in the interval
$E_{0}^{\ast }(g,s)$
has at worst finitely many poles, and they all occur at the integral and half-integral points in the interval
![]() $[0,5]$
. This completes the proof of the statement about the poles of
$[0,5]$
. This completes the proof of the statement about the poles of
 $E_{0}^{\ast }(g,s)$
.
$E_{0}^{\ast }(g,s)$
.
Now for the functional equation. Recall
 $M(f_{s})=c(s)f_{5-s}$
. Then
$M(f_{s})=c(s)f_{5-s}$
. Then
 $c(s)=c_{8}(s)$
is determined above. For
$c(s)=c_{8}(s)$
is determined above. For
![]() $v<\infty$
split, one finds
$v<\infty$
split, one finds
 $$\begin{eqnarray}c_{v}(s)=\frac{\unicode[STIX]{x1D701}_{v}(2s-5)\unicode[STIX]{x1D701}_{v}(2s-7)\unicode[STIX]{x1D701}_{v}(2s-9)}{\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-2)\unicode[STIX]{x1D701}_{v}(2s-4)}.\end{eqnarray}$$
$$\begin{eqnarray}c_{v}(s)=\frac{\unicode[STIX]{x1D701}_{v}(2s-5)\unicode[STIX]{x1D701}_{v}(2s-7)\unicode[STIX]{x1D701}_{v}(2s-9)}{\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-2)\unicode[STIX]{x1D701}_{v}(2s-4)}.\end{eqnarray}$$
For
![]() $v<\infty$
ramified, one gets
$v<\infty$
ramified, one gets
 $$\begin{eqnarray}c_{v}(s)=\frac{\unicode[STIX]{x1D701}_{v}(2s-5)\unicode[STIX]{x1D701}_{v}(2s-7)\unicode[STIX]{x1D701}_{v}(2s-9)}{\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-4)\unicode[STIX]{x1D701}_{v}(2s-8)}.\end{eqnarray}$$
$$\begin{eqnarray}c_{v}(s)=\frac{\unicode[STIX]{x1D701}_{v}(2s-5)\unicode[STIX]{x1D701}_{v}(2s-7)\unicode[STIX]{x1D701}_{v}(2s-9)}{\unicode[STIX]{x1D701}_{v}(2s)\unicode[STIX]{x1D701}_{v}(2s-4)\unicode[STIX]{x1D701}_{v}(2s-8)}.\end{eqnarray}$$
Using the duplication formula
 $\unicode[STIX]{x1D6E4}_{\mathbf{R}}(z)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(z+1)=\unicode[STIX]{x1D6E4}_{\mathbf{C}}(z)$
, one obtains
$\unicode[STIX]{x1D6E4}_{\mathbf{R}}(z)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(z+1)=\unicode[STIX]{x1D6E4}_{\mathbf{C}}(z)$
, one obtains
 $$\begin{eqnarray}c_{\infty }(s)=D_{B}^{-3}\frac{\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s-5)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s-7)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s-9)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)^{2}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-4)^{2}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-8)^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}c_{\infty }(s)=D_{B}^{-3}\frac{\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s-5)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s-7)\unicode[STIX]{x1D6E4}_{\mathbf{C}}(2s-9)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)^{2}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-4)^{2}\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-8)^{2}}.\end{eqnarray}$$
Now, we have
 $$\begin{eqnarray}E_{0}^{\ast }(g,s)=D_{B}^{s}\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-2)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-4)\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\frac{1}{\unicode[STIX]{x1D701}_{v}(2s-2)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-8)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-2)}E_{0}(g,s)\end{eqnarray}$$
$$\begin{eqnarray}E_{0}^{\ast }(g,s)=D_{B}^{s}\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-2)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-4)\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\frac{1}{\unicode[STIX]{x1D701}_{v}(2s-2)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-8)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-2)}E_{0}(g,s)\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(s)=\prod _{v}\unicode[STIX]{x1D701}_{v}(s)$
denotes the completed Riemann zeta function. Thus, since
$\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(s)=\prod _{v}\unicode[STIX]{x1D701}_{v}(s)$
denotes the completed Riemann zeta function. Thus, since
 $\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(s)=\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(1-s)$
,
$\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(s)=\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(1-s)$
,
 $$\begin{eqnarray}\displaystyle E_{0}^{\ast }(g,5-s) & = & \displaystyle D_{B}^{5-s}\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-9)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-7)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-5)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\frac{1}{\unicode[STIX]{x1D701}_{v}(8-2s)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2-2s)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(8-2s)}E_{0}(g,5-s).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{0}^{\ast }(g,5-s) & = & \displaystyle D_{B}^{5-s}\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-9)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-7)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-5)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\frac{1}{\unicode[STIX]{x1D701}_{v}(8-2s)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2-2s)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(8-2s)}E_{0}(g,5-s).\nonumber\end{eqnarray}$$
The intertwining operator gives
 $$\begin{eqnarray}\displaystyle E_{0}^{\ast }(g,s) & = & \displaystyle D_{B}^{s-3}\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-9)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-7)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-5)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\frac{1}{\unicode[STIX]{x1D701}_{v}(2s-8)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-6)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)}E_{0}(g,5-s).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{0}^{\ast }(g,s) & = & \displaystyle D_{B}^{s-3}\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-9)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-7)\unicode[STIX]{x1D6EC}_{\mathbf{Q}}(2s-5)\nonumber\\ \displaystyle & & \displaystyle \times \,\biggl(\mathop{\prod }_{v<\infty ~\text{ramified}}\frac{1}{\unicode[STIX]{x1D701}_{v}(2s-8)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-6)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)}E_{0}(g,5-s).\nonumber\end{eqnarray}$$
Thus
 $$\begin{eqnarray}\frac{E_{0}^{\ast }(g,5-s)}{E_{0}^{\ast }(g,s)}=D_{B}^{8-2s}\biggl(\mathop{\prod }_{v<\infty ~\text{ram}}\frac{\unicode[STIX]{x1D701}_{v}(2s-8)}{\unicode[STIX]{x1D701}_{v}(8-2s)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2-2s)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-6)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(8-2s)}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{E_{0}^{\ast }(g,5-s)}{E_{0}^{\ast }(g,s)}=D_{B}^{8-2s}\biggl(\mathop{\prod }_{v<\infty ~\text{ram}}\frac{\unicode[STIX]{x1D701}_{v}(2s-8)}{\unicode[STIX]{x1D701}_{v}(8-2s)}\biggr)\frac{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2-2s)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s)}{\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s-6)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(8-2s)}.\end{eqnarray}$$
But
 $\unicode[STIX]{x1D701}_{v}(s)/\unicode[STIX]{x1D701}_{v}(-s)=-p^{s}$
, and
$\unicode[STIX]{x1D701}_{v}(s)/\unicode[STIX]{x1D701}_{v}(-s)=-p^{s}$
, and
 $\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2z)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2-2z)=1/(\sin (\unicode[STIX]{x1D70B}z))$
. Thus the above fraction is
$\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2z)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2-2z)=1/(\sin (\unicode[STIX]{x1D70B}z))$
. Thus the above fraction is
 $$\begin{eqnarray}D_{B}^{8-2s}\biggl(\mathop{\prod }_{v<\infty ~\text{ram}}-p^{2s-8}\biggr)\frac{\sin (\unicode[STIX]{x1D70B}(s-3))}{\sin (\unicode[STIX]{x1D70B}s)}=1\end{eqnarray}$$
$$\begin{eqnarray}D_{B}^{8-2s}\biggl(\mathop{\prod }_{v<\infty ~\text{ram}}-p^{2s-8}\biggr)\frac{\sin (\unicode[STIX]{x1D70B}(s-3))}{\sin (\unicode[STIX]{x1D70B}s)}=1\end{eqnarray}$$
since
![]() $B$
is ramified at an even number of places. This completes the proof of Theorem 7.3.
$B$
is ramified at an even number of places. This completes the proof of Theorem 7.3.
7.3 Differential operators
In this section we analyze the normalized Eisenstein series
 $E_{2r}^{\ast }(g,s)$
that is used in the Rankin–Selberg integral for a Siegel modular form on
$E_{2r}^{\ast }(g,s)$
that is used in the Rankin–Selberg integral for a Siegel modular form on
![]() $\operatorname{GSp}_{6}$
of even weight
$\operatorname{GSp}_{6}$
of even weight
![]() $2r$
. In all that follows,
$2r$
. In all that follows,
![]() $r\geqslant 0$
is an integer. This Eisenstein series is defined as follows. At finite places
$r\geqslant 0$
is an integer. This Eisenstein series is defined as follows. At finite places
![]() $p<\infty$
, define
$p<\infty$
, define
![]() $f_{p}^{\ast }(g,s)$
the normalized section as above, so that
$f_{p}^{\ast }(g,s)$
the normalized section as above, so that
 $f_{p}^{\ast }(K_{p},s)=\unicode[STIX]{x1D701}_{p}(2s)\unicode[STIX]{x1D701}_{p}(2s-4)$
if
$f_{p}^{\ast }(K_{p},s)=\unicode[STIX]{x1D701}_{p}(2s)\unicode[STIX]{x1D701}_{p}(2s-4)$
if
![]() $p$
is ramified for
$p$
is ramified for
![]() $B$
, and
$B$
, and
 $f_{p}^{\ast }(K_{p},s)=\unicode[STIX]{x1D701}_{p}(2s)\unicode[STIX]{x1D701}_{p}(2s-2)\unicode[STIX]{x1D701}_{p}(2s-4)$
if
$f_{p}^{\ast }(K_{p},s)=\unicode[STIX]{x1D701}_{p}(2s)\unicode[STIX]{x1D701}_{p}(2s-2)\unicode[STIX]{x1D701}_{p}(2s-4)$
if
![]() $p$
is split for
$p$
is split for
![]() $B$
. At infinity, the normalized section is defined as follows. Define
$B$
. At infinity, the normalized section is defined as follows. Define
![]() $f_{\infty ,2r}$
to be the unique element of
$f_{\infty ,2r}$
to be the unique element of
 $\text{Ind}_{P(\mathbf{R})}^{\text{G}(\mathbf{R})}(\unicode[STIX]{x1D712}_{s})$
that satisfies
$\text{Ind}_{P(\mathbf{R})}^{\text{G}(\mathbf{R})}(\unicode[STIX]{x1D712}_{s})$
that satisfies
 $f_{\infty ,2r}(k,s)=j(k,i)^{2r}$
for all
$f_{\infty ,2r}(k,s)=j(k,i)^{2r}$
for all
 $k\in K_{\infty }$
. Then the normalized section
$k\in K_{\infty }$
. Then the normalized section
 $$\begin{eqnarray}f_{\infty ,2r}^{\ast }(g,s)=\unicode[STIX]{x1D6E4}_{\boldsymbol{ R}}(2s+2r)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-8)f_{\infty ,2r}(g,s).\end{eqnarray}$$
$$\begin{eqnarray}f_{\infty ,2r}^{\ast }(g,s)=\unicode[STIX]{x1D6E4}_{\boldsymbol{ R}}(2s+2r)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-4)\unicode[STIX]{x1D6E4}_{\mathbf{R}}(2s+2r-8)f_{\infty ,2r}(g,s).\end{eqnarray}$$
Finally,
 $$\begin{eqnarray}E_{2r}^{\ast }(g,s)=D_{B}^{s}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash G(\mathbf{Q})}f_{2r}^{\ast }(\unicode[STIX]{x1D6FE}g,s),\end{eqnarray}$$
$$\begin{eqnarray}E_{2r}^{\ast }(g,s)=D_{B}^{s}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in P(\mathbf{Q})\backslash G(\mathbf{Q})}f_{2r}^{\ast }(\unicode[STIX]{x1D6FE}g,s),\end{eqnarray}$$
where
 $f_{2r}^{\ast }(g,s)=f_{\infty ,2r}^{\ast }(g,s)\prod _{v<\infty }f_{v}^{\ast }(g,s)$
. Thus when
$f_{2r}^{\ast }(g,s)=f_{\infty ,2r}^{\ast }(g,s)\prod _{v<\infty }f_{v}^{\ast }(g,s)$
. Thus when
![]() $r=0$
, we recover the spherical normalized Eisenstein series.
$r=0$
, we recover the spherical normalized Eisenstein series.
We will use (essentially) the Maass–Shimura differential operators [Reference MaassMaa71, § 19], [Reference ShimuraShi81] to obtain the desired analytic properties of
 $E_{2r}^{\ast }(g,s)$
from
$E_{2r}^{\ast }(g,s)$
from
 $E_{0}^{\ast }(g,s)$
, as stated in the following theorem.
$E_{0}^{\ast }(g,s)$
, as stated in the following theorem.
Theorem 7.7. There is an element
![]() ${\mathcal{D}}$
of
${\mathcal{D}}$
of
 ${\mathcal{U}}(\mathfrak{g})\otimes \mathbf{C}$
, the complexified universal enveloping algebra of the Lie algebra of
${\mathcal{U}}(\mathfrak{g})\otimes \mathbf{C}$
, the complexified universal enveloping algebra of the Lie algebra of
![]() $\text{G}(\mathbf{R})$
, such that
$\text{G}(\mathbf{R})$
, such that
 ${\mathcal{D}}E_{2r}^{\ast }(g,s)=E_{2r+2}^{\ast }(g,s)$
. Consequently,
${\mathcal{D}}E_{2r}^{\ast }(g,s)=E_{2r+2}^{\ast }(g,s)$
. Consequently,
 $E_{2r}^{\ast }(g,s)=E_{2r}^{\ast }(g,5-s)$
and
$E_{2r}^{\ast }(g,s)=E_{2r}^{\ast }(g,5-s)$
and
 $E_{2r}^{\ast }(g,s)$
has at worst prescribed poles at the integral and half-integral points in the interval
$E_{2r}^{\ast }(g,s)$
has at worst prescribed poles at the integral and half-integral points in the interval
![]() $[0,5]$
.
$[0,5]$
.
The proof will work as follows. First, recall that
 $j(g,i)=\langle r(i)g^{-1},f\rangle$
, so that
$j(g,i)=\langle r(i)g^{-1},f\rangle$
, so that
 $j(tg,i)=t^{-1}j(g,i)$
if
$j(tg,i)=t^{-1}j(g,i)$
if
 $t\in \operatorname{GL}_{1}$
denotes, by slight abuse of notation, the element of
$t\in \operatorname{GL}_{1}$
denotes, by slight abuse of notation, the element of
![]() $\text{G}$
that acts as multiplication by the scalar
$\text{G}$
that acts as multiplication by the scalar
![]() $t$
on
$t$
on
![]() $W$
. Define
$W$
. Define
 $J(g,i)=\unicode[STIX]{x1D708}(g)j(g,i)=\langle r(i),fg\rangle$
, and for
$J(g,i)=\unicode[STIX]{x1D708}(g)j(g,i)=\langle r(i),fg\rangle$
, and for
 $v\in W(\mathbf{R})$
, recall that
$v\in W(\mathbf{R})$
, recall that
 $\unicode[STIX]{x1D6F7}_{\infty ,2r}(v)=e^{-\Vert v\Vert ^{2}}\langle r(i),v\rangle ^{2r}$
. Then
$\unicode[STIX]{x1D6F7}_{\infty ,2r}(v)=e^{-\Vert v\Vert ^{2}}\langle r(i),v\rangle ^{2r}$
. Then
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\infty ,2r}(fg)=e^{-|J(g,i)|^{2}}J(g,i)^{2r}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\infty ,2r}(fg)=e^{-|J(g,i)|^{2}}J(g,i)^{2r}.\end{eqnarray}$$
One has
 $$\begin{eqnarray}f_{\infty ,2r}^{\ast }(g,s)=\unicode[STIX]{x1D70B}^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}(s+r-2)\unicode[STIX]{x1D6E4}(s+r-4)|\unicode[STIX]{x1D708}(g)|^{s}\int _{\operatorname{GL}_{1}(\mathbf{R})}\unicode[STIX]{x1D6F7}_{2r}(tfg)|t|^{2s}\,dt.\end{eqnarray}$$
$$\begin{eqnarray}f_{\infty ,2r}^{\ast }(g,s)=\unicode[STIX]{x1D70B}^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}(s+r-2)\unicode[STIX]{x1D6E4}(s+r-4)|\unicode[STIX]{x1D708}(g)|^{s}\int _{\operatorname{GL}_{1}(\mathbf{R})}\unicode[STIX]{x1D6F7}_{2r}(tfg)|t|^{2s}\,dt.\end{eqnarray}$$
Indeed, the function of
![]() $g$
on the right-hand side of (7.4) is in the correct induction space, has the correct transformation with respect to
$g$
on the right-hand side of (7.4) is in the correct induction space, has the correct transformation with respect to
![]() $K_{\infty }$
, and at
$K_{\infty }$
, and at
![]() $g=1$
is
$g=1$
is
 $\unicode[STIX]{x1D70B}^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(s+r-2)\unicode[STIX]{x1D6E4}(s+r-4)$
since the inner integral at
$\unicode[STIX]{x1D70B}^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(s+r-2)\unicode[STIX]{x1D6E4}(s+r-4)$
since the inner integral at
![]() $g=1$
is
$g=1$
is
 $\unicode[STIX]{x1D6E4}(s+r)$
. Hence this
$\unicode[STIX]{x1D6E4}(s+r)$
. Hence this
![]() $f_{\infty ,2r}^{\ast }$
agrees with normalized section used in the body of the paper. In different notation,
$f_{\infty ,2r}^{\ast }$
agrees with normalized section used in the body of the paper. In different notation,
 $$\begin{eqnarray}f_{\infty ,2r}^{\ast }(g,s)=\unicode[STIX]{x1D70B}^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(s+r-2)\unicode[STIX]{x1D6E4}(s+r-4)|\unicode[STIX]{x1D708}(g)|^{s}\frac{J(g,i)^{2r}}{|J(g,i)|^{2s+2r}}.\end{eqnarray}$$
$$\begin{eqnarray}f_{\infty ,2r}^{\ast }(g,s)=\unicode[STIX]{x1D70B}^{-(3s+3r-6)}\unicode[STIX]{x1D6E4}(s+r)\unicode[STIX]{x1D6E4}(s+r-2)\unicode[STIX]{x1D6E4}(s+r-4)|\unicode[STIX]{x1D708}(g)|^{s}\frac{J(g,i)^{2r}}{|J(g,i)|^{2s+2r}}.\end{eqnarray}$$
To compute the action of
![]() ${\mathcal{D}}$
on
${\mathcal{D}}$
on
 $f_{\infty ,2r}^{\ast }(g,s)$
and thus
$f_{\infty ,2r}^{\ast }(g,s)$
and thus
 $E_{2r}^{\ast }(g,s)$
, we compute it on the function of
$E_{2r}^{\ast }(g,s)$
, we compute it on the function of
![]() $g$
$g$
 $g\mapsto \unicode[STIX]{x1D6F7}_{\infty ,2r}(fg)$
. We will find
$g\mapsto \unicode[STIX]{x1D6F7}_{\infty ,2r}(fg)$
. We will find
 $$\begin{eqnarray}{\mathcal{D}}\unicode[STIX]{x1D6F7}_{\infty ,2r}(fg)=\unicode[STIX]{x1D70B}^{-3}e^{-|J(g,i)|^{2}}\{|J(g,i)|^{4}-9|J(g,i)|^{2}+15\}J(g,i)^{2r+2}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}\unicode[STIX]{x1D6F7}_{\infty ,2r}(fg)=\unicode[STIX]{x1D70B}^{-3}e^{-|J(g,i)|^{2}}\{|J(g,i)|^{4}-9|J(g,i)|^{2}+15\}J(g,i)^{2r+2}.\end{eqnarray}$$
Now since
 $$\begin{eqnarray}\int _{\operatorname{GL}_{1}(\mathbf{R})}e^{-t^{2}|J(g,i)|^{2}}|J(g,i)|^{2v}J(g,i)^{2r+2}|t|^{2s+2r+2+2v}\,dt=\unicode[STIX]{x1D6E4}(s+r+1+v)\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}},\end{eqnarray}$$
$$\begin{eqnarray}\int _{\operatorname{GL}_{1}(\mathbf{R})}e^{-t^{2}|J(g,i)|^{2}}|J(g,i)|^{2v}J(g,i)^{2r+2}|t|^{2s+2r+2+2v}\,dt=\unicode[STIX]{x1D6E4}(s+r+1+v)\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}},\end{eqnarray}$$
(7.5) implies
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\operatorname{GL}_{1}(\mathbf{R})}{\mathcal{D}}\unicode[STIX]{x1D6F7}_{\infty ,2r}(tg)|t|^{2s}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70B}^{-3}\{\unicode[STIX]{x1D6E4}(s+r+3)-9\unicode[STIX]{x1D6E4}(s+r+2)+15\unicode[STIX]{x1D6E4}(s+r+1)\}\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70B}^{-3}\{(s+r+2)(s+r+1)-9(s+r+1)+15\}\unicode[STIX]{x1D6E4}(s+r+1)\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70B}^{-3}(s+r-2)(s+r-4)\unicode[STIX]{x1D6E4}(s+r+1)\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\operatorname{GL}_{1}(\mathbf{R})}{\mathcal{D}}\unicode[STIX]{x1D6F7}_{\infty ,2r}(tg)|t|^{2s}\,dt\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70B}^{-3}\{\unicode[STIX]{x1D6E4}(s+r+3)-9\unicode[STIX]{x1D6E4}(s+r+2)+15\unicode[STIX]{x1D6E4}(s+r+1)\}\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70B}^{-3}\{(s+r+2)(s+r+1)-9(s+r+1)+15\}\unicode[STIX]{x1D6E4}(s+r+1)\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D70B}^{-3}(s+r-2)(s+r-4)\unicode[STIX]{x1D6E4}(s+r+1)\frac{J(g,i)^{2r+2}}{|J(g,i)|^{2s+2r+2}}.\nonumber\end{eqnarray}$$
Thus Theorem 7.7 follows as soon as we establish (7.5).
Let us now define
![]() ${\mathcal{D}}$
and prove the identity (7.5). Set
${\mathcal{D}}$
and prove the identity (7.5). Set
 $h=n(i)\overline{n}(i/2)\in \text{G}(\mathbf{C})$
. Then
$h=n(i)\overline{n}(i/2)\in \text{G}(\mathbf{C})$
. Then
 $r(i)h=e$
and
$r(i)h=e$
and
 $r(-i)h=-8if$
. Denote by
$r(-i)h=-8if$
. Denote by
![]() $\overline{\mathfrak{u}_{P}}(\mathbf{R})$
the Lie algebra of the unipotent subgroup of
$\overline{\mathfrak{u}_{P}}(\mathbf{R})$
the Lie algebra of the unipotent subgroup of
![]() $\text{G}(\mathbf{R})$
consisting of the
$\text{G}(\mathbf{R})$
consisting of the
![]() $\overline{n}(X)$
, for
$\overline{n}(X)$
, for
 $X\in J_{\mathbf{R}}$
, with
$X\in J_{\mathbf{R}}$
, with
 $J=H_{3}(B)$
. We will define
$J=H_{3}(B)$
. We will define
![]() ${\mathcal{D}}_{0}$
in
${\mathcal{D}}_{0}$
in
 ${\mathcal{U}}(\overline{\mathfrak{u}_{P}}(\mathbf{R}))\simeq \operatorname{Sym}(J_{\mathbf{R}})$
, the universal enveloping algebra of
${\mathcal{U}}(\overline{\mathfrak{u}_{P}}(\mathbf{R}))\simeq \operatorname{Sym}(J_{\mathbf{R}})$
, the universal enveloping algebra of
![]() $\overline{\mathfrak{u}_{P}}(\mathbf{R})$
, and then
$\overline{\mathfrak{u}_{P}}(\mathbf{R})$
, and then
![]() ${\mathcal{D}}$
will be given by
${\mathcal{D}}$
will be given by
 $(2\unicode[STIX]{x1D70B}i)^{-3}h{\mathcal{D}}_{0}h^{-1}$
. Here we identify
$(2\unicode[STIX]{x1D70B}i)^{-3}h{\mathcal{D}}_{0}h^{-1}$
. Here we identify
![]() $J$
with
$J$
with
![]() $\overline{\mathfrak{u}_{P}}$
via the logarithm
$\overline{\mathfrak{u}_{P}}$
via the logarithm
![]() $\overline{L}$
of the map
$\overline{L}$
of the map
![]() $\overline{n}$
. One has
$\overline{n}$
. One has
 $$\begin{eqnarray}(a,b,c,d)\overline{L}(X)=(\operatorname{tr}(b,X),c\times X,dX,0).\end{eqnarray}$$
$$\begin{eqnarray}(a,b,c,d)\overline{L}(X)=(\operatorname{tr}(b,X),c\times X,dX,0).\end{eqnarray}$$
To define
![]() ${\mathcal{D}}_{0}$
, we first rewrite the formula for the norm of an element of
${\mathcal{D}}_{0}$
, we first rewrite the formula for the norm of an element of
![]() $J$
in coordinates. For
$J$
in coordinates. For
![]() $a\in B_{\mathbf{R}}$
, denote by
$a\in B_{\mathbf{R}}$
, denote by
 $a(1),a(i),a(j),a(k)$
the real numbers defined by the equality
$a(1),a(i),a(j),a(k)$
the real numbers defined by the equality
 $a=a(1)+a(i)i+a(j)j+a(k)k$
. If
$a=a(1)+a(i)i+a(j)j+a(k)k$
. If
 $$\begin{eqnarray}x=\left(\begin{array}{@{}ccc@{}}c_{1} & a_{3} & a_{2}^{\ast }\\ a_{3}^{\ast } & c_{2} & a_{1}\\ a_{2} & a_{1}^{\ast } & c_{3}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}x=\left(\begin{array}{@{}ccc@{}}c_{1} & a_{3} & a_{2}^{\ast }\\ a_{3}^{\ast } & c_{2} & a_{1}\\ a_{2} & a_{1}^{\ast } & c_{3}\end{array}\right),\end{eqnarray}$$
then
 $$\begin{eqnarray}\displaystyle N(x) & = & \displaystyle c_{1}c_{2}c_{3}-\biggl(\mathop{\sum }_{i=1,2,3}\mathop{\sum }_{u\in \{1,i,j,k\}}c_{i}a_{i}(u)^{2}\biggr)+2a_{1}(1)a_{2}(1)a_{3}(1)\nonumber\\ \displaystyle & & \displaystyle -\,2\biggl(\mathop{\sum }_{i=1,2,3}\mathop{\sum }_{u\in \{i,j,k\}}a_{i}(1)a_{i+1}(u)a_{i+2}(u)\biggr)-2\det (a_{j}(u)).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N(x) & = & \displaystyle c_{1}c_{2}c_{3}-\biggl(\mathop{\sum }_{i=1,2,3}\mathop{\sum }_{u\in \{1,i,j,k\}}c_{i}a_{i}(u)^{2}\biggr)+2a_{1}(1)a_{2}(1)a_{3}(1)\nonumber\\ \displaystyle & & \displaystyle -\,2\biggl(\mathop{\sum }_{i=1,2,3}\mathop{\sum }_{u\in \{i,j,k\}}a_{i}(1)a_{i+1}(u)a_{i+2}(u)\biggr)-2\det (a_{j}(u)).\end{eqnarray}$$
Here
 $$\begin{eqnarray}(a_{j}(u))=\left(\begin{array}{@{}ccc@{}}a_{1}(i) & a_{2}(i) & a_{3}(i)\\ a_{1}(j) & a_{2}(j) & a_{3}(j)\\ a_{1}(k) & a_{2}(k) & a_{3}(k)\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}(a_{j}(u))=\left(\begin{array}{@{}ccc@{}}a_{1}(i) & a_{2}(i) & a_{3}(i)\\ a_{1}(j) & a_{2}(j) & a_{3}(j)\\ a_{1}(k) & a_{2}(k) & a_{3}(k)\end{array}\right).\end{eqnarray}$$
View the coordinates
 $c_{i},a_{j}(u)$
on the right-hand side of (7.6) as elements of
$c_{i},a_{j}(u)$
on the right-hand side of (7.6) as elements of
![]() $J^{\vee }$
, the dual of
$J^{\vee }$
, the dual of
![]() $J$
, so that the expression becomes an element of
$J$
, so that the expression becomes an element of
 $\operatorname{Sym}^{3}(J^{\vee })$
. The trace form
$\operatorname{Sym}^{3}(J^{\vee })$
. The trace form
![]() $\operatorname{tr}(\;,\;)$
gives an identification
$\operatorname{tr}(\;,\;)$
gives an identification
![]() $J\simeq J^{\vee }$
, and thus the norm gives us an element
$J\simeq J^{\vee }$
, and thus the norm gives us an element
![]() ${\mathcal{D}}_{0}$
of
${\mathcal{D}}_{0}$
of
 $\operatorname{Sym}^{3}(J)\subseteq {\mathcal{U}}(\overline{\mathfrak{u}_{P}})\subseteq {\mathcal{U}}(\mathfrak{g})$
. This is the differential operator
$\operatorname{Sym}^{3}(J)\subseteq {\mathcal{U}}(\overline{\mathfrak{u}_{P}})\subseteq {\mathcal{U}}(\mathfrak{g})$
. This is the differential operator
![]() ${\mathcal{D}}_{0}$
defined above. More explicitly, recall that
${\mathcal{D}}_{0}$
defined above. More explicitly, recall that
![]() $e_{ij}$
denotes the element of
$e_{ij}$
denotes the element of
![]() $M_{3}(B)$
with a
$M_{3}(B)$
with a
![]() $1$
at position
$1$
at position
![]() $i,j$
and zeroes elsewhere. Define
$i,j$
and zeroes elsewhere. Define
 $v_{1}(u)=ue_{23}+u^{\ast }e_{32}$
, and similarly for
$v_{1}(u)=ue_{23}+u^{\ast }e_{32}$
, and similarly for
![]() $v_{2}(u)$
,
$v_{2}(u)$
,
![]() $v_{3}(u)$
. Then under the identification of
$v_{3}(u)$
. Then under the identification of
![]() $J^{\vee }$
with
$J^{\vee }$
with
![]() $J$
,
$J$
,
![]() $c_{i}$
becomes
$c_{i}$
becomes
![]() $e_{ii}$
and
$e_{ii}$
and
![]() $a_{i}(u)$
becomes
$a_{i}(u)$
becomes
![]() $v_{i}(u)/2$
. Hence
$v_{i}(u)/2$
. Hence
 $$\begin{eqnarray}\displaystyle {\mathcal{D}}_{0} & = & \displaystyle e_{11}e_{22}e_{33}-\frac{1}{4}\biggl(\mathop{\sum }_{1\leqslant i\leqslant 3,u\in \{1,i,j,k\}}e_{ii}v_{i}(u)^{2}\biggr)+\frac{1}{4}v_{1}(1)v_{2}(1)v_{3}(1)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4}\biggl(\mathop{\sum }_{1\leqslant i\leqslant 3,u\in \{i,j,k\}}v_{i}(1)v_{i+1}(u)v_{i+2}(u)\biggr)-\frac{1}{4}\det (v_{j}(u)).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{D}}_{0} & = & \displaystyle e_{11}e_{22}e_{33}-\frac{1}{4}\biggl(\mathop{\sum }_{1\leqslant i\leqslant 3,u\in \{1,i,j,k\}}e_{ii}v_{i}(u)^{2}\biggr)+\frac{1}{4}v_{1}(1)v_{2}(1)v_{3}(1)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{1}{4}\biggl(\mathop{\sum }_{1\leqslant i\leqslant 3,u\in \{i,j,k\}}v_{i}(1)v_{i+1}(u)v_{i+2}(u)\biggr)-\frac{1}{4}\det (v_{j}(u)).\end{eqnarray}$$
Now
![]() ${\mathcal{D}}$
is a product of terms of the form
${\mathcal{D}}$
is a product of terms of the form
 $D(x):=h\overline{L}(-x)h^{-1}$
, for
$D(x):=h\overline{L}(-x)h^{-1}$
, for
![]() $x\in J$
. Let us compute the action of such a term on
$x\in J$
. Let us compute the action of such a term on
 $\langle r(i),fg\rangle$
and
$\langle r(i),fg\rangle$
and
 $\langle r(-i),fg\rangle$
.
$\langle r(-i),fg\rangle$
.
Lemma 7.8.
 $D(x)\langle r(i),fg\rangle =0$
.
$D(x)\langle r(i),fg\rangle =0$
.
 $D(x)\langle r(-i),fg\rangle =-8i\langle (0,0,x,0),fgh\rangle$
.
$D(x)\langle r(-i),fg\rangle =-8i\langle (0,0,x,0),fgh\rangle$
.
Proof. We have
 $$\begin{eqnarray}\langle r(i),fghe^{t\overline{L}(-x)}h^{-1}\rangle =\langle ee^{t\overline{L}(x)},fgh\rangle =\langle e,fgh\rangle\end{eqnarray}$$
$$\begin{eqnarray}\langle r(i),fghe^{t\overline{L}(-x)}h^{-1}\rangle =\langle ee^{t\overline{L}(x)},fgh\rangle =\langle e,fgh\rangle\end{eqnarray}$$
is independent of
![]() $t$
, proving the first claim. Similarly,
$t$
, proving the first claim. Similarly,
 $$\begin{eqnarray}\langle r(-i),fghe^{t\overline{L}(-x)}h^{-1}\rangle =-8i\langle fe^{t\overline{L}(x)},fgh\rangle =-8i\langle f,fgh\rangle -8it\langle (0,0,x,0),fgh\rangle +O(t^{2})\end{eqnarray}$$
$$\begin{eqnarray}\langle r(-i),fghe^{t\overline{L}(-x)}h^{-1}\rangle =-8i\langle fe^{t\overline{L}(x)},fgh\rangle =-8i\langle f,fgh\rangle -8it\langle (0,0,x,0),fgh\rangle +O(t^{2})\end{eqnarray}$$
proving the second statement. ◻
We now compute
 $D(z)D(y)D(x)e^{-|J(g,i)|^{2}}$
. First, since
$D(z)D(y)D(x)e^{-|J(g,i)|^{2}}$
. First, since
 $|J(g,i)|^{2}=\langle r(i),fg\rangle \langle r(-i),fg\rangle$
,
$|J(g,i)|^{2}=\langle r(i),fg\rangle \langle r(-i),fg\rangle$
,
 $$\begin{eqnarray}D(x)e^{-|J(g,i)|^{2}}=e^{-|J(g,i)|^{2}}J(g,i)(8i\langle (0,0,x,0),fgh\rangle )=e^{-|J(g,i)|^{2}}\langle (0,0,x,0),v\rangle\end{eqnarray}$$
$$\begin{eqnarray}D(x)e^{-|J(g,i)|^{2}}=e^{-|J(g,i)|^{2}}J(g,i)(8i\langle (0,0,x,0),fgh\rangle )=e^{-|J(g,i)|^{2}}\langle (0,0,x,0),v\rangle\end{eqnarray}$$
where
 $v=8iJ(g,i)fgh$
. Now, we have
$v=8iJ(g,i)fgh$
. Now, we have
 $D(y)\langle (0,0,x,0),fgh\rangle =\langle (0,x\times y,0,0),fgh\rangle$
. Continuing, we thus get
$D(y)\langle (0,0,x,0),fgh\rangle =\langle (0,x\times y,0,0),fgh\rangle$
. Continuing, we thus get
 $$\begin{eqnarray}D(y)D(x)e^{-|J(g,i)|^{2}}=e^{-|J(g,i)|^{2}}\{\langle (0,0,y,0),v\rangle \langle (0,0,x,0),v\rangle +\langle (0,x\times y,0,0),v\rangle \}.\end{eqnarray}$$
$$\begin{eqnarray}D(y)D(x)e^{-|J(g,i)|^{2}}=e^{-|J(g,i)|^{2}}\{\langle (0,0,y,0),v\rangle \langle (0,0,x,0),v\rangle +\langle (0,x\times y,0,0),v\rangle \}.\end{eqnarray}$$
Finally,
 $$\begin{eqnarray}D(z)D(y)D(x)e^{-|J(g,i)|^{2}}=e^{-|J(g,i)|^{2}}(D_{1}(x,y,z)(v)+D_{2}(x,y,z)(v)+D_{3}(x,y,z)(v)),\end{eqnarray}$$
$$\begin{eqnarray}D(z)D(y)D(x)e^{-|J(g,i)|^{2}}=e^{-|J(g,i)|^{2}}(D_{1}(x,y,z)(v)+D_{2}(x,y,z)(v)+D_{3}(x,y,z)(v)),\end{eqnarray}$$
where, for
 $x,y,z\in J$
and
$x,y,z\in J$
and
![]() $w\in W$
,
$w\in W$
,
 $$\begin{eqnarray}\displaystyle D_{1}(x,y,z)(w) & = & \displaystyle \langle (0,0,x,0),w\rangle \langle (0,0,y,0),w\rangle \langle (0,0,z,0),w\rangle ,\nonumber\\ \displaystyle D_{2}(x,y,z)(w) & = & \displaystyle \langle (0,0,x,0),w\rangle \langle (0,y\times z,0,0),w\rangle +\langle (0,0,y,0),w\rangle \langle (0,z\times x,0,0),w\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle (0,0,z,0),w\rangle \langle (0,x\times y,0,0),w\rangle ,\nonumber\\ \displaystyle D_{3}(x,y,z)(w) & = & \displaystyle \langle (\operatorname{tr}(z,x\times y),0,0,0),w\rangle .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{1}(x,y,z)(w) & = & \displaystyle \langle (0,0,x,0),w\rangle \langle (0,0,y,0),w\rangle \langle (0,0,z,0),w\rangle ,\nonumber\\ \displaystyle D_{2}(x,y,z)(w) & = & \displaystyle \langle (0,0,x,0),w\rangle \langle (0,y\times z,0,0),w\rangle +\langle (0,0,y,0),w\rangle \langle (0,z\times x,0,0),w\rangle \nonumber\\ \displaystyle & & \displaystyle +\,\langle (0,0,z,0),w\rangle \langle (0,x\times y,0,0),w\rangle ,\nonumber\\ \displaystyle D_{3}(x,y,z)(w) & = & \displaystyle \langle (\operatorname{tr}(z,x\times y),0,0,0),w\rangle .\nonumber\end{eqnarray}$$
Proposition 7.9. Write
 ${\mathcal{D}}_{0}=\sum \unicode[STIX]{x1D6FC}\,xyz$
,
${\mathcal{D}}_{0}=\sum \unicode[STIX]{x1D6FC}\,xyz$
,
![]() $\unicode[STIX]{x1D6FC}\in \mathbf{R}$
,
$\unicode[STIX]{x1D6FC}\in \mathbf{R}$
,
 $x,y,z\in J$
, as abstract expression for the right-hand side of (7.7). Suppose
$x,y,z\in J$
, as abstract expression for the right-hand side of (7.7). Suppose
 $w=(a,b,c,d)$
. Then
$w=(a,b,c,d)$
. Then
 $$\begin{eqnarray}\sum \unicode[STIX]{x1D6FC}D_{1}(x,y,z)(w)=\det (b);\quad \sum \unicode[STIX]{x1D6FC}D_{2}(x,y,z)(w)=-3\operatorname{tr}(b,c);\quad \sum \unicode[STIX]{x1D6FC}D_{3}(x,y,z)(w)=15d.\end{eqnarray}$$
$$\begin{eqnarray}\sum \unicode[STIX]{x1D6FC}D_{1}(x,y,z)(w)=\det (b);\quad \sum \unicode[STIX]{x1D6FC}D_{2}(x,y,z)(w)=-3\operatorname{tr}(b,c);\quad \sum \unicode[STIX]{x1D6FC}D_{3}(x,y,z)(w)=15d.\end{eqnarray}$$
Proof. This is a straightforward but tedious calculation, so we omit it. ◻
Recall that
 $v=8iJ(g,i)fgh=:(a,b,c,d)$
. We obtain
$v=8iJ(g,i)fgh=:(a,b,c,d)$
. We obtain
 $$\begin{eqnarray}(8i)^{-1}h(-{\mathcal{D}}_{0})h^{-1}e^{-|J(g,i)|^{2}}=(8i)^{-1}e^{-|J(g,i)|^{2}}(\det (b)-3\operatorname{tr}(b,c)+15d).\end{eqnarray}$$
$$\begin{eqnarray}(8i)^{-1}h(-{\mathcal{D}}_{0})h^{-1}e^{-|J(g,i)|^{2}}=(8i)^{-1}e^{-|J(g,i)|^{2}}(\det (b)-3\operatorname{tr}(b,c)+15d).\end{eqnarray}$$
But now,
 $$\begin{eqnarray}a=\langle -f,v\rangle =J(g,i)\langle r(-i),fg\rangle =|J(g,i)|^{2}\end{eqnarray}$$
$$\begin{eqnarray}a=\langle -f,v\rangle =J(g,i)\langle r(-i),fg\rangle =|J(g,i)|^{2}\end{eqnarray}$$
and
 $$\begin{eqnarray}d=\langle e,v\rangle =8iJ(g,i)\langle r(i),fg\rangle =8iJ(g,i)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}d=\langle e,v\rangle =8iJ(g,i)\langle r(i),fg\rangle =8iJ(g,i)^{2}.\end{eqnarray}$$
Since
 $v=(a,b,c,d)$
is rank one,
$v=(a,b,c,d)$
is rank one,
 $\det (b)=a^{2}d$
and
$\det (b)=a^{2}d$
and
 $\operatorname{tr}(b,c)=3ad$
. Thus
$\operatorname{tr}(b,c)=3ad$
. Thus
 $$\begin{eqnarray}\det (b)-3\operatorname{tr}(b,c)+15d=8i\{|J(g,i)|^{4}J(g,i)^{2}-9|J(g,i)|^{2}J(g,i)^{2}+15J(g,i)^{2}\}.\end{eqnarray}$$
$$\begin{eqnarray}\det (b)-3\operatorname{tr}(b,c)+15d=8i\{|J(g,i)|^{4}J(g,i)^{2}-9|J(g,i)|^{2}J(g,i)^{2}+15J(g,i)^{2}\}.\end{eqnarray}$$
Hence
 $$\begin{eqnarray}(2\unicode[STIX]{x1D70B}i)^{-3}h{\mathcal{D}}_{0}h^{-1}e^{-|J(g,i)|^{2}}=\unicode[STIX]{x1D70B}^{-3}\{|J(g,i)|^{4}-9|J(g,i)|^{2}+15\}J(g,i)^{2}e^{-|J(g,i)|^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}(2\unicode[STIX]{x1D70B}i)^{-3}h{\mathcal{D}}_{0}h^{-1}e^{-|J(g,i)|^{2}}=\unicode[STIX]{x1D70B}^{-3}\{|J(g,i)|^{4}-9|J(g,i)|^{2}+15\}J(g,i)^{2}e^{-|J(g,i)|^{2}}.\end{eqnarray}$$
Since all the differential operators act trivially on the
![]() $J(g,i)$
, we get
$J(g,i)$
, we get
 $$\begin{eqnarray}{\mathcal{D}}(J(g,i)^{2r}e^{-|J(g,i)|^{2}})=\unicode[STIX]{x1D70B}^{-3}\{|J(g,i)|^{4}-9|J(g,i)|^{2}+15\}J(g,i)^{2r+2}e^{-|J(g,i)|^{2}},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}(J(g,i)^{2r}e^{-|J(g,i)|^{2}})=\unicode[STIX]{x1D70B}^{-3}\{|J(g,i)|^{4}-9|J(g,i)|^{2}+15\}J(g,i)^{2r+2}e^{-|J(g,i)|^{2}},\end{eqnarray}$$
Acknowledgements
It is a pleasure to thank Shrenik Shah for his collaboration on [Reference Pollack and ShahPS15], without which this work might never have come to fruition. We are grateful to Benedict Gross, Mark Lucianovic, Ila Varma, and Akshay Venkatesh for enlightening conversations. We also thank Siegfried Böcherer, Gordan Savin and John Voight for their very helpful comments on an earlier version of this manuscript.
Appendix A Relation with
 $\operatorname{GU}_{6}(B)$
$\operatorname{GU}_{6}(B)$
As above, we assume our ground field
![]() $F$
is of characteristic zero, and
$F$
is of characteristic zero, and
![]() $B$
denotes a quaternion algebra over
$B$
denotes a quaternion algebra over
![]() $F$
. To emphasize the relationship to the quaternion algebra
$F$
. To emphasize the relationship to the quaternion algebra
![]() $B$
, we write
$B$
, we write
 $\text{G}_{B}=\text{G}$
for the group of linear automorphisms of
$\text{G}_{B}=\text{G}$
for the group of linear automorphisms of
 $W_{B}=F\oplus H_{3}(B)\oplus H_{3}(B)\oplus F$
that preserve the symplectic and quartic form, up to similitude. Set
$W_{B}=F\oplus H_{3}(B)\oplus H_{3}(B)\oplus F$
that preserve the symplectic and quartic form, up to similitude. Set
![]() $J_{6}$
, as usual, to be the matrix
$J_{6}$
, as usual, to be the matrix
![]() $(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!)$
. Define
$(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!)$
. Define
 $\operatorname{GU}_{6}(B)$
to be the pairs
$\operatorname{GU}_{6}(B)$
to be the pairs
 $(g,\unicode[STIX]{x1D708})\in \operatorname{GL}_{6}(B)\times \operatorname{GL}_{1}$
that satisfy
$(g,\unicode[STIX]{x1D708})\in \operatorname{GL}_{6}(B)\times \operatorname{GL}_{1}$
that satisfy
 $gJ_{6}g^{\ast }=\unicode[STIX]{x1D708}(g)J_{6}$
. The group
$gJ_{6}g^{\ast }=\unicode[STIX]{x1D708}(g)J_{6}$
. The group
![]() $\text{G}_{B}$
is closely related to
$\text{G}_{B}$
is closely related to
 $\operatorname{GU}_{6}(B)$
. In this section, we work out an explicit relationship. The results of this section are not needed in the proof of Theorem 1.2; we have included this section only to help orient the reader.
$\operatorname{GU}_{6}(B)$
. In this section, we work out an explicit relationship. The results of this section are not needed in the proof of Theorem 1.2; we have included this section only to help orient the reader.
The explicit relationship between
![]() $\text{G}_{B}$
and
$\text{G}_{B}$
and
 $\operatorname{GU}_{6}(B)$
takes the following form. We define a reductive
$\operatorname{GU}_{6}(B)$
takes the following form. We define a reductive
![]() $F$
-group
$F$
-group
![]() $\widetilde{G}$
, that satisfies the following two properties.
$\widetilde{G}$
, that satisfies the following two properties.
-
– There are natural, explicit maps
 $\widetilde{G}\rightarrow \text{G}_{B}$
and
$\widetilde{G}\rightarrow \text{G}_{B}$
and
 $\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
, that are surjective on
$\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
, that are surjective on
 $\overline{F}$
points, where
$\overline{F}$
points, where
 $\overline{F}$
is an algebraic closure of
$\overline{F}$
is an algebraic closure of
 $F$
.
$F$
. -
– The kernels of the two maps from
 $\widetilde{G}$
are (distinct)
$\widetilde{G}$
are (distinct)
 $\unicode[STIX]{x1D707}_{2}$
values in the center of
$\unicode[STIX]{x1D707}_{2}$
values in the center of
 $\widetilde{G}$
.
$\widetilde{G}$
.
To define
![]() $\widetilde{G}$
, we proceed as follows. First, we make an octonion algebra
$\widetilde{G}$
, we proceed as follows. First, we make an octonion algebra
![]() $\unicode[STIX]{x1D6E9}$
out of
$\unicode[STIX]{x1D6E9}$
out of
![]() $B$
using the Cayley–Dickson construction. Denote by
$B$
using the Cayley–Dickson construction. Denote by
 $W_{\unicode[STIX]{x1D6E9}}=F\oplus H_{3}(\unicode[STIX]{x1D6E9})\oplus H_{3}(\unicode[STIX]{x1D6E9})\oplus F$
the Freudenthal space made out of the cubic Jordan algebra of Hermitian
$W_{\unicode[STIX]{x1D6E9}}=F\oplus H_{3}(\unicode[STIX]{x1D6E9})\oplus H_{3}(\unicode[STIX]{x1D6E9})\oplus F$
the Freudenthal space made out of the cubic Jordan algebra of Hermitian
![]() $3\times 3$
matrices over
$3\times 3$
matrices over
![]() $\unicode[STIX]{x1D6E9}$
. Next, we define a decomposition
$\unicode[STIX]{x1D6E9}$
. Next, we define a decomposition
 $W_{\unicode[STIX]{x1D6E9}}=W_{B}\oplus W_{6}\otimes B$
. This decomposition induces an action of
$W_{\unicode[STIX]{x1D6E9}}=W_{B}\oplus W_{6}\otimes B$
. This decomposition induces an action of
 $\text{G}_{B}\times \operatorname{GU}_{6}(B)$
on
$\text{G}_{B}\times \operatorname{GU}_{6}(B)$
on
![]() $W_{\unicode[STIX]{x1D6E9}}$
, with
$W_{\unicode[STIX]{x1D6E9}}$
, with
![]() $\text{G}_{B}$
acting via its defining representation on
$\text{G}_{B}$
acting via its defining representation on
![]() $W_{B}$
and as the identity on
$W_{B}$
and as the identity on
 $W_{6}\otimes B$
, and vice versa for
$W_{6}\otimes B$
, and vice versa for
 $\operatorname{GU}_{6}(B)$
. We define
$\operatorname{GU}_{6}(B)$
. We define
![]() $\widetilde{G}$
to be the set of pairs
$\widetilde{G}$
to be the set of pairs
 $(g,h)\in \text{G}_{B}\times \operatorname{GU}_{6}(B)$
that preserve the symplectic and quartic form on
$(g,h)\in \text{G}_{B}\times \operatorname{GU}_{6}(B)$
that preserve the symplectic and quartic form on
![]() $W_{\unicode[STIX]{x1D6E9}}$
, up to similitude. The natural maps
$W_{\unicode[STIX]{x1D6E9}}$
, up to similitude. The natural maps
 $\widetilde{G}\rightarrow \text{G}_{B}$
and
$\widetilde{G}\rightarrow \text{G}_{B}$
and
 $\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
are then the projections.
$\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
are then the projections.
A.1 The Cayley–Dickson construction
Fix a
 $\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{1}(F)$
. Then the octonion algebra
$\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{1}(F)$
. Then the octonion algebra
![]() $\unicode[STIX]{x1D6E9}$
is defined to be the pairs
$\unicode[STIX]{x1D6E9}$
is defined to be the pairs
![]() $(x,y)$
,
$(x,y)$
,
![]() $x,y$
in
$x,y$
in
![]() $B$
, with addition defined component-wise, and multiplication as
$B$
, with addition defined component-wise, and multiplication as
 $$\begin{eqnarray}(x_{1},y_{1})(x_{2},y_{2})=(x_{1}x_{2}+\unicode[STIX]{x1D6FE}y_{2}^{\ast }y_{1},y_{2}x_{1}+y_{1}x_{2}^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}(x_{1},y_{1})(x_{2},y_{2})=(x_{1}x_{2}+\unicode[STIX]{x1D6FE}y_{2}^{\ast }y_{1},y_{2}x_{1}+y_{1}x_{2}^{\ast }).\end{eqnarray}$$
The conjugation on
![]() $\unicode[STIX]{x1D6E9}$
is
$\unicode[STIX]{x1D6E9}$
is
 $(x,y)^{\ast }=(x^{\ast },-y)$
. If
$(x,y)^{\ast }=(x^{\ast },-y)$
. If
 $z=(x,y)$
is in
$z=(x,y)$
is in
![]() $\unicode[STIX]{x1D6E9}$
, then
$\unicode[STIX]{x1D6E9}$
, then
 $\operatorname{tr}(z):=z+z^{\ast }=\operatorname{tr}(x)$
and
$\operatorname{tr}(z):=z+z^{\ast }=\operatorname{tr}(x)$
and
 $n(z)=zz^{\ast }=n(x)-\unicode[STIX]{x1D6FE}n(y)$
. The choice
$n(z)=zz^{\ast }=n(x)-\unicode[STIX]{x1D6FE}n(y)$
. The choice
![]() $\unicode[STIX]{x1D6FE}=-1$
is usually made to define the positive-definite octonion algebra.
$\unicode[STIX]{x1D6FE}=-1$
is usually made to define the positive-definite octonion algebra.
Recall that the multiplication in
![]() $\unicode[STIX]{x1D6E9}$
is not associative, but that one does have the identity
$\unicode[STIX]{x1D6E9}$
is not associative, but that one does have the identity
 $\operatorname{tr}((z_{1}z_{2})z_{3})=\operatorname{tr}(z_{1}(z_{2}z_{3}))$
for
$\operatorname{tr}((z_{1}z_{2})z_{3})=\operatorname{tr}(z_{1}(z_{2}z_{3}))$
for
 $z_{1},z_{2},z_{3}\in \unicode[STIX]{x1D6E9}$
.
$z_{1},z_{2},z_{3}\in \unicode[STIX]{x1D6E9}$
.
A.2 The space
 $W_{\unicode[STIX]{x1D6E9}}$
$W_{\unicode[STIX]{x1D6E9}}$
The map
![]() $B\rightarrow \unicode[STIX]{x1D6E9}$
,
$B\rightarrow \unicode[STIX]{x1D6E9}$
,
 $b\mapsto (b,0)$
, induces an obvious inclusion
$b\mapsto (b,0)$
, induces an obvious inclusion
 $W_{B}\rightarrow W_{\unicode[STIX]{x1D6E9}}$
. We define
$W_{B}\rightarrow W_{\unicode[STIX]{x1D6E9}}$
. We define
 $\unicode[STIX]{x1D704}:W_{6}\otimes B\rightarrow W_{\unicode[STIX]{x1D6E9}}$
as follows. Suppose
$\unicode[STIX]{x1D704}:W_{6}\otimes B\rightarrow W_{\unicode[STIX]{x1D6E9}}$
as follows. Suppose
 $w\in W_{6}\otimes B$
is
$w\in W_{6}\otimes B$
is
 $b_{1}e_{1}+b_{2}e_{2}+b_{3}e_{3}+c_{1}f_{1}+c_{2}f_{2}+c_{3}f_{3}$
, with
$b_{1}e_{1}+b_{2}e_{2}+b_{3}e_{3}+c_{1}f_{1}+c_{2}f_{2}+c_{3}f_{3}$
, with
 $b_{i},c_{j}\in B$
. Then
$b_{i},c_{j}\in B$
. Then
![]() $\unicode[STIX]{x1D704}(w)$
is defined to be
$\unicode[STIX]{x1D704}(w)$
is defined to be
 $(0,B,C,0)\in W_{\unicode[STIX]{x1D6E9}}$
, with
$(0,B,C,0)\in W_{\unicode[STIX]{x1D6E9}}$
, with
 $$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}} & (0,-b_{3}) & (0,b_{2})\\ (0,b_{3}) & & (0,-b_{1})\\ (0,-b_{2}) & (0,b_{1}) & \end{array}\right)\quad \text{and}\quad C=\left(\begin{array}{@{}ccc@{}} & (0,c_{3}) & (0,-c_{2})\\ (0,-c_{3}) & & (0,c_{1})\\ (0,c_{2}) & (0,-c_{1}) & \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}B=\left(\begin{array}{@{}ccc@{}} & (0,-b_{3}) & (0,b_{2})\\ (0,b_{3}) & & (0,-b_{1})\\ (0,-b_{2}) & (0,b_{1}) & \end{array}\right)\quad \text{and}\quad C=\left(\begin{array}{@{}ccc@{}} & (0,c_{3}) & (0,-c_{2})\\ (0,-c_{3}) & & (0,c_{1})\\ (0,c_{2}) & (0,-c_{1}) & \end{array}\right).\end{eqnarray}$$
(The difference in minus signs is intentional.) It is clear that
 $W_{\unicode[STIX]{x1D6E9}}=W_{B}\oplus \unicode[STIX]{x1D704}(W_{6}\otimes B)$
.
$W_{\unicode[STIX]{x1D6E9}}=W_{B}\oplus \unicode[STIX]{x1D704}(W_{6}\otimes B)$
.
We now list some useful formulas. Denote by
![]() $\langle \;,\;\rangle _{B}$
the
$\langle \;,\;\rangle _{B}$
the
![]() $B$
-valued symplectic-Hermitian form on
$B$
-valued symplectic-Hermitian form on
 $W_{6}\otimes B$
preserved by
$W_{6}\otimes B$
preserved by
 $\operatorname{GU}_{6}(B)$
. That is, if
$\operatorname{GU}_{6}(B)$
. That is, if
 $w=\sum _{i}b_{i}e_{i}+\sum _{i}c_{i}f_{i}$
, and
$w=\sum _{i}b_{i}e_{i}+\sum _{i}c_{i}f_{i}$
, and
 $w^{\prime }=\sum _{i}b_{i}^{\prime }e_{i}+\sum _{i}c_{i}^{\prime }f_{i}$
, then
$w^{\prime }=\sum _{i}b_{i}^{\prime }e_{i}+\sum _{i}c_{i}^{\prime }f_{i}$
, then
 $\langle w,w^{\prime }\rangle _{B}=\sum _{i}b_{i}(c_{i}^{\prime })^{\ast }-\sum _{i}c_{i}(b_{i}^{\prime })^{\ast }$
.
$\langle w,w^{\prime }\rangle _{B}=\sum _{i}b_{i}(c_{i}^{\prime })^{\ast }-\sum _{i}c_{i}(b_{i}^{\prime })^{\ast }$
.
-
– With
 $B,C$
as in (A.1),
$B,C$
as in (A.1),
 $\operatorname{tr}(B,C)=\unicode[STIX]{x1D6FE}((b_{1},c_{1})+(b_{2},c_{2})+(b_{3},c_{3}))$
.
$\operatorname{tr}(B,C)=\unicode[STIX]{x1D6FE}((b_{1},c_{1})+(b_{2},c_{2})+(b_{3},c_{3}))$
. -
– The symplectic form on
 $W_{\unicode[STIX]{x1D6E9}}$
restricts to the form
$W_{\unicode[STIX]{x1D6E9}}$
restricts to the form
 $(-\unicode[STIX]{x1D6FE})\langle \;,\;\rangle \otimes (\;,\;)$
on
$(-\unicode[STIX]{x1D6FE})\langle \;,\;\rangle \otimes (\;,\;)$
on
 $W_{6}\otimes B$
. That is, if
$W_{6}\otimes B$
. That is, if
 $w=\sum _{i}b_{i}e_{i}+\sum _{i}c_{i}f_{i}$
, and
$w=\sum _{i}b_{i}e_{i}+\sum _{i}c_{i}f_{i}$
, and
 $w^{\prime }=\sum _{i}b_{i}^{\prime }e_{i}+\sum _{i}c_{i}^{\prime }f_{i}$
, then (A.2)
$w^{\prime }=\sum _{i}b_{i}^{\prime }e_{i}+\sum _{i}c_{i}^{\prime }f_{i}$
, then (A.2) $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D704}(w),\unicode[STIX]{x1D704}(w^{\prime })\rangle & = & \displaystyle -\unicode[STIX]{x1D6FE}\biggl(\mathop{\sum }_{i}(b_{i},c_{i}^{\prime })-\mathop{\sum }_{i}(c_{i},b_{i}^{\prime })\biggr)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FE}\operatorname{tr}(\langle w,w^{\prime }\rangle _{B}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D704}(w),\unicode[STIX]{x1D704}(w^{\prime })\rangle & = & \displaystyle -\unicode[STIX]{x1D6FE}\biggl(\mathop{\sum }_{i}(b_{i},c_{i}^{\prime })-\mathop{\sum }_{i}(c_{i},b_{i}^{\prime })\biggr)\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FE}\operatorname{tr}(\langle w,w^{\prime }\rangle _{B}).\end{eqnarray}$$
-
– If
then $$\begin{eqnarray}Y=\left(\begin{array}{@{}ccc@{}} & (0,y_{3}) & (0,-y_{2})\\ (0,-y_{3}) & & (0,y_{1})\\ (0,y_{2}) & (0,-y_{1}) & \end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}Y=\left(\begin{array}{@{}ccc@{}} & (0,y_{3}) & (0,-y_{2})\\ (0,-y_{3}) & & (0,y_{1})\\ (0,y_{2}) & (0,-y_{1}) & \end{array}\right),\end{eqnarray}$$
 $$\begin{eqnarray}Y^{\#}=\unicode[STIX]{x1D6FE}\left(\begin{array}{@{}c@{}}y_{1}^{\ast }\\ y_{2}^{\ast }\\ y_{3}^{\ast }\end{array}\right)\left(\begin{array}{@{}ccc@{}}y_{1} & y_{2} & y_{3}\end{array}\right)=\unicode[STIX]{x1D6FE}\left(\begin{array}{@{}ccc@{}}n(y_{1}) & y_{1}^{\ast }y_{2} & y_{1}^{\ast }y_{3}\\ y_{2}^{\ast }y_{1} & n(y_{2}) & y_{2}^{\ast }y_{3}\\ y_{3}^{\ast }y_{1} & y_{3}^{\ast }y_{2} & n(y_{3})\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}Y^{\#}=\unicode[STIX]{x1D6FE}\left(\begin{array}{@{}c@{}}y_{1}^{\ast }\\ y_{2}^{\ast }\\ y_{3}^{\ast }\end{array}\right)\left(\begin{array}{@{}ccc@{}}y_{1} & y_{2} & y_{3}\end{array}\right)=\unicode[STIX]{x1D6FE}\left(\begin{array}{@{}ccc@{}}n(y_{1}) & y_{1}^{\ast }y_{2} & y_{1}^{\ast }y_{3}\\ y_{2}^{\ast }y_{1} & n(y_{2}) & y_{2}^{\ast }y_{3}\\ y_{3}^{\ast }y_{1} & y_{3}^{\ast }y_{2} & n(y_{3})\end{array}\right).\end{eqnarray}$$
-
– We have
 $Q(\unicode[STIX]{x1D704}(w))=-\unicode[STIX]{x1D6FE}^{2}N(\langle w,w\rangle _{B})$
. Indeed, suppose
$Q(\unicode[STIX]{x1D704}(w))=-\unicode[STIX]{x1D6FE}^{2}N(\langle w,w\rangle _{B})$
. Indeed, suppose
 $w=(0,B,C,0)$
, with
$w=(0,B,C,0)$
, with
 $B,C$
as in (A.1). Define
$B,C$
as in (A.1). Define
 $v_{b}=(b_{1},b_{2},b_{3})$
and define
$v_{b}=(b_{1},b_{2},b_{3})$
and define
 $v_{c}$
similarly. Then
$v_{c}$
similarly. Then  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}^{-2}Q(\unicode[STIX]{x1D704}(w)) & = & \displaystyle \unicode[STIX]{x1D6FE}^{-2}\operatorname{tr}(B,C)^{2}-4\unicode[STIX]{x1D6FE}^{-2}\operatorname{tr}(B^{\#},C^{\#})\nonumber\\ \displaystyle & = & \displaystyle \biggl(\mathop{\sum }_{i}(b_{i},c_{i})\biggr)^{2}-4\operatorname{tr}(v_{b}^{\ast }v_{b},v_{c}^{\ast }v_{c})\nonumber\\ \displaystyle & = & \displaystyle \operatorname{tr}(v_{b}v_{c}^{\ast })^{2}-4n(v_{b}v_{c}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle -n(v_{b}v_{c}^{\ast }-v_{c}v_{b}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle -n(\langle w,w\rangle _{B}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}^{-2}Q(\unicode[STIX]{x1D704}(w)) & = & \displaystyle \unicode[STIX]{x1D6FE}^{-2}\operatorname{tr}(B,C)^{2}-4\unicode[STIX]{x1D6FE}^{-2}\operatorname{tr}(B^{\#},C^{\#})\nonumber\\ \displaystyle & = & \displaystyle \biggl(\mathop{\sum }_{i}(b_{i},c_{i})\biggr)^{2}-4\operatorname{tr}(v_{b}^{\ast }v_{b},v_{c}^{\ast }v_{c})\nonumber\\ \displaystyle & = & \displaystyle \operatorname{tr}(v_{b}v_{c}^{\ast })^{2}-4n(v_{b}v_{c}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle -n(v_{b}v_{c}^{\ast }-v_{c}v_{b}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle -n(\langle w,w\rangle _{B}).\nonumber\end{eqnarray}$$
-
– For
 $b=(b_{1},b_{2},b_{3})$
and
$b=(b_{1},b_{2},b_{3})$
and
 $c=(c_{1},c_{2},c_{3})$
in
$c=(c_{1},c_{2},c_{3})$
in
 $B^{3}$
, let us write
$B^{3}$
, let us write
 $\unicode[STIX]{x1D704}_{e}(b)=B$
,
$\unicode[STIX]{x1D704}_{e}(b)=B$
,
 $\unicode[STIX]{x1D704}_{f}(c)=C$
, with
$\unicode[STIX]{x1D704}_{f}(c)=C$
, with
 $B,C$
as in (A.1). Then if
$B,C$
as in (A.1). Then if
 $X,Y$
in
$X,Y$
in
 $J=H_{3}(B)$
, (A.3)
$J=H_{3}(B)$
, (A.3) $$\begin{eqnarray}X\times \unicode[STIX]{x1D704}_{e}(b)=\unicode[STIX]{x1D704}_{f}(bX)\quad \text{and}\quad Y\times \unicode[STIX]{x1D704}_{f}(c)=\unicode[STIX]{x1D704}_{e}(cY).\end{eqnarray}$$
$$\begin{eqnarray}X\times \unicode[STIX]{x1D704}_{e}(b)=\unicode[STIX]{x1D704}_{f}(bX)\quad \text{and}\quad Y\times \unicode[STIX]{x1D704}_{f}(c)=\unicode[STIX]{x1D704}_{e}(cY).\end{eqnarray}$$
-
– Suppose
 $v\in W_{B}$
,
$v\in W_{B}$
,
 $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D704}(W_{6}\otimes B)$
. Then
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D704}(W_{6}\otimes B)$
. Then
 $(v,v,v,\unicode[STIX]{x1D6FF})=0$
and
$(v,v,v,\unicode[STIX]{x1D6FF})=0$
and
 $(v,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF})=0$
. Suppose
$(v,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF})=0$
. Suppose
 $v=(a,b,c,d)$
and
$v=(a,b,c,d)$
and
 $\unicode[STIX]{x1D6FF}=(0,B,C,0)$
. Then
$\unicode[STIX]{x1D6FF}=(0,B,C,0)$
. Then
 $(v,v,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF})$
is proportional to (by a nonzero constant) (A.4)
$(v,v,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF})$
is proportional to (by a nonzero constant) (A.4) $$\begin{eqnarray}\operatorname{tr}(B,C)(ad-\operatorname{tr}(b,c))+\operatorname{tr}(b\times B,c\times C)+2\operatorname{tr}(B^{\#},c^{\#}-db)+2\operatorname{tr}(C^{\#},b^{\#}-ac).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{tr}(B,C)(ad-\operatorname{tr}(b,c))+\operatorname{tr}(b\times B,c\times C)+2\operatorname{tr}(B^{\#},c^{\#}-db)+2\operatorname{tr}(C^{\#},b^{\#}-ac).\end{eqnarray}$$
A.3 The group
 $\widetilde{G}$
$\widetilde{G}$
We now have enough formulae to easily prove the facts about
![]() $\widetilde{G}$
claimed above. First note that, by (A.2),
$\widetilde{G}$
claimed above. First note that, by (A.2),
 $(g,h)\in \text{G}_{B}\times \operatorname{GU}_{6}(B)$
preserves the symplectic form on
$(g,h)\in \text{G}_{B}\times \operatorname{GU}_{6}(B)$
preserves the symplectic form on
![]() $W_{\unicode[STIX]{x1D6E9}}$
if and only if
$W_{\unicode[STIX]{x1D6E9}}$
if and only if
 $\unicode[STIX]{x1D708}(g)=\unicode[STIX]{x1D708}(h)$
.
$\unicode[STIX]{x1D708}(g)=\unicode[STIX]{x1D708}(h)$
.
Now we construct some explicit elements in
![]() $\widetilde{G}$
. First, if
$\widetilde{G}$
. First, if
 $X\in H_{3}(B)$
, then one computes
$X\in H_{3}(B)$
, then one computes
 $n_{\unicode[STIX]{x1D6E9}}(X)=(n_{B}(X),(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!))$
, and thus
$n_{\unicode[STIX]{x1D6E9}}(X)=(n_{B}(X),(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!))$
, and thus
![]() $n_{\unicode[STIX]{x1D6E9}}(X)$
is an element of
$n_{\unicode[STIX]{x1D6E9}}(X)$
is an element of
![]() $\widetilde{G}$
. The equality
$\widetilde{G}$
. The equality
 $n_{\unicode[STIX]{x1D6E9}}(X)=(n_{B}(X),(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!))$
follows from (A.3). Next, one verifies immediately that the following are all elements of
$n_{\unicode[STIX]{x1D6E9}}(X)=(n_{B}(X),(\!\begin{smallmatrix}1 & X\\ & 1\end{smallmatrix}\!))$
follows from (A.3). Next, one verifies immediately that the following are all elements of
![]() $\widetilde{G}$
.
$\widetilde{G}$
.
-
–
 $J_{\unicode[STIX]{x1D6E9}}=(J_{B},(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!))$
. Here
$J_{\unicode[STIX]{x1D6E9}}=(J_{B},(\!\begin{smallmatrix} & 1_{3}\\ -1_{3} & \end{smallmatrix}\!))$
. Here
 $J_{B},J_{\unicode[STIX]{x1D6E9}}$
act on
$J_{B},J_{\unicode[STIX]{x1D6E9}}$
act on
 $W_{B}$
, respectively
$W_{B}$
, respectively
 $W_{\unicode[STIX]{x1D6E9}}$
, as
$W_{\unicode[STIX]{x1D6E9}}$
, as
 $(a,b,c,d)\mapsto (-d,c,-b,a)$
.
$(a,b,c,d)\mapsto (-d,c,-b,a)$
. -
–
 $m_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})=(m_{B}(\unicode[STIX]{x1D706}),(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & 1\end{smallmatrix}\!))$
. Here
$m_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})=(m_{B}(\unicode[STIX]{x1D706}),(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & 1\end{smallmatrix}\!))$
. Here
 $m_{B}(\unicode[STIX]{x1D706}),m_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})$
act on
$m_{B}(\unicode[STIX]{x1D706}),m_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})$
act on
 $W_{B}$
, respectively
$W_{B}$
, respectively
 $W_{\unicode[STIX]{x1D6E9}}$
, as
$W_{\unicode[STIX]{x1D6E9}}$
, as
 $(a,b,c,d)\mapsto (\unicode[STIX]{x1D706}^{2}a,\unicode[STIX]{x1D706}b,c,\unicode[STIX]{x1D706}^{-1}d)$
.
$(a,b,c,d)\mapsto (\unicode[STIX]{x1D706}^{2}a,\unicode[STIX]{x1D706}b,c,\unicode[STIX]{x1D706}^{-1}d)$
. -
–
 $z_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})=(z_{B}(\unicode[STIX]{x1D706}),(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & \unicode[STIX]{x1D706}\end{smallmatrix}\!))$
. Here
$z_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})=(z_{B}(\unicode[STIX]{x1D706}),(\!\begin{smallmatrix}\unicode[STIX]{x1D706} & \\ & \unicode[STIX]{x1D706}\end{smallmatrix}\!))$
. Here
 $z_{B}(\unicode[STIX]{x1D706}),z_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})$
act on
$z_{B}(\unicode[STIX]{x1D706}),z_{\unicode[STIX]{x1D6E9}}(\unicode[STIX]{x1D706})$
act on
 $W_{B}$
, respectively
$W_{B}$
, respectively
 $W_{\unicode[STIX]{x1D6E9}}$
, as
$W_{\unicode[STIX]{x1D6E9}}$
, as
 $(a,b,c,d)\mapsto \unicode[STIX]{x1D706}(a,b,c,d)$
.
$(a,b,c,d)\mapsto \unicode[STIX]{x1D706}(a,b,c,d)$
.
Now suppose
 $m\in \operatorname{GL}_{3}(B)$
, and
$m\in \operatorname{GL}_{3}(B)$
, and
 $N(m^{\ast }m)$
is a square in
$N(m^{\ast }m)$
is a square in
![]() $F^{\times }$
, say
$F^{\times }$
, say
 $N(m^{\ast }m)=\unicode[STIX]{x1D6FF}^{2}$
. Associated to such a pair
$N(m^{\ast }m)=\unicode[STIX]{x1D6FF}^{2}$
. Associated to such a pair
![]() $(m,\unicode[STIX]{x1D6FF})$
, we construct an element
$(m,\unicode[STIX]{x1D6FF})$
, we construct an element
 $(M(m,\unicode[STIX]{x1D6FF}),(\!\begin{smallmatrix}m & \\ & \text{}^{\ast }m^{-1}\end{smallmatrix}\!))$
in
$(M(m,\unicode[STIX]{x1D6FF}),(\!\begin{smallmatrix}m & \\ & \text{}^{\ast }m^{-1}\end{smallmatrix}\!))$
in
![]() $\widetilde{G}$
. To do this, define
$\widetilde{G}$
. To do this, define
 $M(m,\unicode[STIX]{x1D6FF})$
by
$M(m,\unicode[STIX]{x1D6FF})$
by
 $$\begin{eqnarray}(a,b,c,d)M(m,\unicode[STIX]{x1D6FF})=(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D6FF}m^{-1}b\text{}^{\ast }m^{-1},\unicode[STIX]{x1D6FF}^{-1}m^{\ast }cm,\unicode[STIX]{x1D6FF}^{-1}d).\end{eqnarray}$$
$$\begin{eqnarray}(a,b,c,d)M(m,\unicode[STIX]{x1D6FF})=(\unicode[STIX]{x1D6FF}a,\unicode[STIX]{x1D6FF}m^{-1}b\text{}^{\ast }m^{-1},\unicode[STIX]{x1D6FF}^{-1}m^{\ast }cm,\unicode[STIX]{x1D6FF}^{-1}d).\end{eqnarray}$$
If
 $b\in H_{3}(B)$
, then
$b\in H_{3}(B)$
, then
 $N(\unicode[STIX]{x1D6FF}m^{-1}b\text{}^{\ast }m^{-1})=\unicode[STIX]{x1D6FF}^{3}N(m^{\ast }m)^{-1}N(b)=\unicode[STIX]{x1D6FF}N(b)$
, and hence
$N(\unicode[STIX]{x1D6FF}m^{-1}b\text{}^{\ast }m^{-1})=\unicode[STIX]{x1D6FF}^{3}N(m^{\ast }m)^{-1}N(b)=\unicode[STIX]{x1D6FF}N(b)$
, and hence
 $M(m,\unicode[STIX]{x1D6FF})$
defines an element of
$M(m,\unicode[STIX]{x1D6FF})$
defines an element of
![]() $\text{G}_{B}^{1}$
. To check that
$\text{G}_{B}^{1}$
. To check that
 $(M(m,\unicode[STIX]{x1D6FF}),(\!\begin{smallmatrix}m & \\ & \text{}^{\ast }m^{-1}\end{smallmatrix}\!))$
defines an element of
$(M(m,\unicode[STIX]{x1D6FF}),(\!\begin{smallmatrix}m & \\ & \text{}^{\ast }m^{-1}\end{smallmatrix}\!))$
defines an element of
![]() $\widetilde{G}$
, we must see that the map
$\widetilde{G}$
, we must see that the map
 $$\begin{eqnarray}X+\unicode[STIX]{x1D704}_{f}(c)\mapsto \unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm+\unicode[STIX]{x1D704}_{f}(c\text{}^{\ast }m^{-1})\end{eqnarray}$$
$$\begin{eqnarray}X+\unicode[STIX]{x1D704}_{f}(c)\mapsto \unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm+\unicode[STIX]{x1D704}_{f}(c\text{}^{\ast }m^{-1})\end{eqnarray}$$
on
![]() $H_{3}(\unicode[STIX]{x1D6E9})$
multiples the norm by
$H_{3}(\unicode[STIX]{x1D6E9})$
multiples the norm by
![]() $\unicode[STIX]{x1D6FF}^{-1}$
. But indeed,
$\unicode[STIX]{x1D6FF}^{-1}$
. But indeed,
 $N(X+\unicode[STIX]{x1D704}_{f}(c))=N(X)+\operatorname{tr}(X,\unicode[STIX]{x1D704}_{f}(c)^{\#})$
, and then
$N(X+\unicode[STIX]{x1D704}_{f}(c))=N(X)+\operatorname{tr}(X,\unicode[STIX]{x1D704}_{f}(c)^{\#})$
, and then
 $$\begin{eqnarray}\displaystyle N(\unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm+\unicode[STIX]{x1D704}_{f}(c\text{}^{\ast }m^{-1})) & = & \displaystyle N(\unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm)+\operatorname{tr}(\unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm,\unicode[STIX]{x1D704}_{f}(c\text{}^{\ast }m^{-1})^{\#})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}^{-1}N(X)+\unicode[STIX]{x1D6FF}^{-1}\operatorname{tr}(m^{\ast }Xm,m^{-1}v_{c}^{\ast }v_{c}\text{}^{\ast }m^{-1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}^{-1}N(X)+\unicode[STIX]{x1D6FF}^{-1}\operatorname{tr}(X,v_{c}^{\ast }v_{c})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}^{-1}N(X+\unicode[STIX]{x1D704}_{f}(c)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N(\unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm+\unicode[STIX]{x1D704}_{f}(c\text{}^{\ast }m^{-1})) & = & \displaystyle N(\unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm)+\operatorname{tr}(\unicode[STIX]{x1D6FF}^{-1}m^{\ast }Xm,\unicode[STIX]{x1D704}_{f}(c\text{}^{\ast }m^{-1})^{\#})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}^{-1}N(X)+\unicode[STIX]{x1D6FF}^{-1}\operatorname{tr}(m^{\ast }Xm,m^{-1}v_{c}^{\ast }v_{c}\text{}^{\ast }m^{-1})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}^{-1}N(X)+\unicode[STIX]{x1D6FF}^{-1}\operatorname{tr}(X,v_{c}^{\ast }v_{c})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6FF}^{-1}N(X+\unicode[STIX]{x1D704}_{f}(c)).\nonumber\end{eqnarray}$$
The explicit constructions now prove that
 $\widetilde{G}\rightarrow \text{G}_{B}$
and
$\widetilde{G}\rightarrow \text{G}_{B}$
and
 $\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
are surjections on
$\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
are surjections on
![]() $\overline{F}$
-points.
$\overline{F}$
-points.
Let us now prove that the kernels of the maps
 $\widetilde{G}\rightarrow \text{G}_{B}$
and
$\widetilde{G}\rightarrow \text{G}_{B}$
and
 $\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
are each
$\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
are each
![]() $\unicode[STIX]{x1D707}_{2}$
. First, one checks easily that
$\unicode[STIX]{x1D707}_{2}$
. First, one checks easily that
 $\unicode[STIX]{x1D707}_{2}\times \unicode[STIX]{x1D707}_{2}\subseteq \widetilde{G}$
via
$\unicode[STIX]{x1D707}_{2}\times \unicode[STIX]{x1D707}_{2}\subseteq \widetilde{G}$
via
 $(\pm 1,\pm 1)$
, with the elements
$(\pm 1,\pm 1)$
, with the elements
![]() $\pm 1$
acting by scalar multiplication on
$\pm 1$
acting by scalar multiplication on
![]() $W_{B}$
and
$W_{B}$
and
 $W_{6}\otimes B$
. Hence a
$W_{6}\otimes B$
. Hence a
![]() $\unicode[STIX]{x1D707}_{2}$
is contained in the each of the kernels. Now for the converse.
$\unicode[STIX]{x1D707}_{2}$
is contained in the each of the kernels. Now for the converse.
First consider the map
 $\widetilde{G}\rightarrow \text{G}_{B}$
, and suppose
$\widetilde{G}\rightarrow \text{G}_{B}$
, and suppose
![]() $(1,h)$
is in the kernel. Then
$(1,h)$
is in the kernel. Then
 $\unicode[STIX]{x1D708}(h)=1$
, and the element
$\unicode[STIX]{x1D708}(h)=1$
, and the element
![]() $(1,h)$
of
$(1,h)$
of
![]() $\text{G}_{\unicode[STIX]{x1D6E9}}$
fixes
$\text{G}_{\unicode[STIX]{x1D6E9}}$
fixes
 $(1,0,0,0)$
and
$(1,0,0,0)$
and
 $(0,0,0,1)$
. It follows that it preserves the spaces
$(0,0,0,1)$
. It follows that it preserves the spaces
 $(0,\ast ,0,0)$
and
$(0,\ast ,0,0)$
and
 $(0,0,\ast ,0)$
, and thus
$(0,0,\ast ,0)$
, and thus
 $h=(\!\begin{smallmatrix}m & \\ & \text{}^{\ast }m^{-1}\end{smallmatrix}\!)$
for some
$h=(\!\begin{smallmatrix}m & \\ & \text{}^{\ast }m^{-1}\end{smallmatrix}\!)$
for some
 $m\in \operatorname{GL}_{3}(B)$
. Furthermore, we must have that
$m\in \operatorname{GL}_{3}(B)$
. Furthermore, we must have that
 $N(X+\unicode[STIX]{x1D704}_{e}(b))=N(X+\unicode[STIX]{x1D704}_{e}(bm))$
for all
$N(X+\unicode[STIX]{x1D704}_{e}(b))=N(X+\unicode[STIX]{x1D704}_{e}(bm))$
for all
![]() $X$
in
$X$
in
![]() $H_{3}(B)$
and
$H_{3}(B)$
and
![]() $b\in B^{3}$
, and thus
$b\in B^{3}$
, and thus
 $$\begin{eqnarray}\operatorname{tr}(X,\unicode[STIX]{x1D704}_{e}(bm)^{\#})=\operatorname{tr}(X,m^{\ast }v_{b}^{\ast }v_{b}m)=\operatorname{tr}(mXm^{\ast },v_{b}^{\ast }v_{b})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{tr}(X,\unicode[STIX]{x1D704}_{e}(bm)^{\#})=\operatorname{tr}(X,m^{\ast }v_{b}^{\ast }v_{b}m)=\operatorname{tr}(mXm^{\ast },v_{b}^{\ast }v_{b})\end{eqnarray}$$
is preserved for all
![]() $b,X$
. Since the rank-one elements of the form
$b,X$
. Since the rank-one elements of the form
![]() $v_{b}^{\ast }v_{b}$
span
$v_{b}^{\ast }v_{b}$
span
![]() $H_{3}(B)$
, we have
$H_{3}(B)$
, we have
 $mXm^{\ast }=X$
for all
$mXm^{\ast }=X$
for all
 $X\in H_{3}(B)$
, and thus
$X\in H_{3}(B)$
, and thus
 $m=\pm 1$
, as desired.
$m=\pm 1$
, as desired.
Now consider the map
 $\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
, and suppose
$\widetilde{G}\rightarrow \operatorname{GU}_{6}(B)$
, and suppose
![]() $(g,1)$
is in the kernel. Again we have
$(g,1)$
is in the kernel. Again we have
 $\unicode[STIX]{x1D708}(g)=1$
. We will show
$\unicode[STIX]{x1D708}(g)=1$
. We will show
![]() $g=\pm 1$
by considering the fact that
$g=\pm 1$
by considering the fact that
![]() $(g,1)$
preserves
$(g,1)$
preserves
 $(v,v,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF})$
. By taking
$(v,v,\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6FF})$
. By taking
![]() $C=0$
and letting
$C=0$
and letting
![]() $B$
vary in (A.4), we see
$B$
vary in (A.4), we see
![]() $g$
fixes the quantity
$g$
fixes the quantity
 $c^{\#}-db$
, since the rank-one elements
$c^{\#}-db$
, since the rank-one elements
 $B^{\#}=v_{b}^{\ast }v_{b}$
span
$B^{\#}=v_{b}^{\ast }v_{b}$
span
![]() $H_{3}(B)$
. Similarly, by taking
$H_{3}(B)$
. Similarly, by taking
![]() $B=0$
in (A.4), we see
$B=0$
in (A.4), we see
![]() $g$
fixes the quantity
$g$
fixes the quantity
 $b^{\#}-ac$
.
$b^{\#}-ac$
.
Set
 $f=(0,0,0,1)$
, and suppose
$f=(0,0,0,1)$
, and suppose
 $fg=(A,B,C,D)$
,
$fg=(A,B,C,D)$
,
 $(a,b,c,d)g=(a^{\prime },b^{\prime },c^{\prime },d^{\prime })$
. Then for any
$(a,b,c,d)g=(a^{\prime },b^{\prime },c^{\prime },d^{\prime })$
. Then for any
![]() $\unicode[STIX]{x1D706}\in F$
we get
$\unicode[STIX]{x1D706}\in F$
we get
 $$\begin{eqnarray}\displaystyle b^{\#}-ac & = & \displaystyle (b^{\prime }+\unicode[STIX]{x1D706}B)^{\#}-(a^{\prime }+\unicode[STIX]{x1D706}A)(c^{\prime }+\unicode[STIX]{x1D706}C)\nonumber\\ \displaystyle & = & \displaystyle (b^{\prime })^{\#}-a^{\prime }c^{\prime }+\unicode[STIX]{x1D706}(b^{\prime }\times B-a^{\prime }C-Ac^{\prime }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b^{\#}-ac & = & \displaystyle (b^{\prime }+\unicode[STIX]{x1D706}B)^{\#}-(a^{\prime }+\unicode[STIX]{x1D706}A)(c^{\prime }+\unicode[STIX]{x1D706}C)\nonumber\\ \displaystyle & = & \displaystyle (b^{\prime })^{\#}-a^{\prime }c^{\prime }+\unicode[STIX]{x1D706}(b^{\prime }\times B-a^{\prime }C-Ac^{\prime }),\nonumber\end{eqnarray}$$
and thus
 $b^{\prime }\times B-a^{\prime }C-Ac^{\prime }=0$
. By varying
$b^{\prime }\times B-a^{\prime }C-Ac^{\prime }=0$
. By varying
 $(a,b,c,d)$
, we can make
$(a,b,c,d)$
, we can make
![]() $a^{\prime },b^{\prime },c^{\prime }$
arbitrary. It follows that
$a^{\prime },b^{\prime },c^{\prime }$
arbitrary. It follows that
 $A=B=C=0$
. Similarly, since
$A=B=C=0$
. Similarly, since
![]() $g$
fixes
$g$
fixes
 $c^{\#}-db$
,
$c^{\#}-db$
,
![]() $g$
preserves the line
$g$
preserves the line
 $F(1,0,0,0)$
. Hence,
$F(1,0,0,0)$
. Hence,
 $(1,0,0,0)g=\unicode[STIX]{x1D706}(1,0,0,0)$
, and
$(1,0,0,0)g=\unicode[STIX]{x1D706}(1,0,0,0)$
, and
 $(0,0,0,1)g=\unicode[STIX]{x1D706}^{-1}(0,0,0,1)$
for some
$(0,0,0,1)g=\unicode[STIX]{x1D706}^{-1}(0,0,0,1)$
for some
![]() $\unicode[STIX]{x1D706}\in F^{\times }$
. It follows that
$\unicode[STIX]{x1D706}\in F^{\times }$
. It follows that
![]() $g$
preserves the spaces
$g$
preserves the spaces
 $(0,\ast ,0,0)$
and
$(0,\ast ,0,0)$
and
 $(0,0,\ast ,0)$
in
$(0,0,\ast ,0)$
in
![]() $W_{\unicode[STIX]{x1D6E9}}$
as well, and scales the norm on
$W_{\unicode[STIX]{x1D6E9}}$
as well, and scales the norm on
 $H_{3}(\unicode[STIX]{x1D6E9})=(0,\ast ,0,0)$
by
$H_{3}(\unicode[STIX]{x1D6E9})=(0,\ast ,0,0)$
by
![]() $\unicode[STIX]{x1D706}$
. Write
$\unicode[STIX]{x1D706}$
. Write
 $X\mapsto t(X)$
for the action on
$X\mapsto t(X)$
for the action on
![]() $g$
on
$g$
on
 $H_{3}(B)=(0,\ast ,0,0)$
in
$H_{3}(B)=(0,\ast ,0,0)$
in
![]() $W_{B}$
. Then we have
$W_{B}$
. Then we have
 $\operatorname{tr}(t(X),v_{b}^{\ast }v_{b})=\unicode[STIX]{x1D706}\operatorname{tr}(X,v_{b}^{\ast }v_{b})$
for all
$\operatorname{tr}(t(X),v_{b}^{\ast }v_{b})=\unicode[STIX]{x1D706}\operatorname{tr}(X,v_{b}^{\ast }v_{b})$
for all
 $X\in H_{3}(B)$
,
$X\in H_{3}(B)$
,
![]() $b\in B^{3}$
. Hence
$b\in B^{3}$
. Hence
 $t(X)=\unicode[STIX]{x1D706}X$
. But since
$t(X)=\unicode[STIX]{x1D706}X$
. But since
![]() $t$
also scales the norm by
$t$
also scales the norm by
![]() $\unicode[STIX]{x1D706}$
, we get
$\unicode[STIX]{x1D706}$
, we get
![]() $\unicode[STIX]{x1D706}^{3}=\unicode[STIX]{x1D706}$
, and hence
$\unicode[STIX]{x1D706}^{3}=\unicode[STIX]{x1D706}$
, and hence
![]() $\unicode[STIX]{x1D706}=\pm 1$
, as desired. This completes the proof of the facts about
$\unicode[STIX]{x1D706}=\pm 1$
, as desired. This completes the proof of the facts about
![]() $\widetilde{G}$
.
$\widetilde{G}$
.
Appendix B The magic triangle of Deligne and Gross
In this section we very briefly describe the magic triangle of Deligne and Gross [Reference Deligne and GrossDG02], and its mysterious apparent connection to some Rankin–Selberg integrals. This possible connection appears to be closely related to the so-called towers of Rankin–Selberg integrals introduced by Ginzburg and Rallis [Reference Ginzburg and RallisGR94]. That there may be a connection between the Freudenthal magic square and Rankin–Selberg integrals is discussed, from a different point of view, in Bump’s survey article [Reference BumpBum05].
The magic triangle is an extension of the Freudenthal magic square. Roughly speaking, each row of the triangle contains a sequence of groups
 $H_{1}\subseteq H_{2}\subseteq H_{3}\subseteq \cdots \,$
, each group included in the next. And the groups in the same row all share similar properties. The final row of the triangle is the exceptional series of Deligne [Reference DeligneDel96, Reference Deligne and de ManDdM96]:
$H_{1}\subseteq H_{2}\subseteq H_{3}\subseteq \cdots \,$
, each group included in the next. And the groups in the same row all share similar properties. The final row of the triangle is the exceptional series of Deligne [Reference DeligneDel96, Reference Deligne and de ManDdM96]:
 $$\begin{eqnarray}A_{1}\subset A_{2}\subset G_{2}\subset D_{4}\subset F_{4}\subset E_{6}\subset E_{7}\subset E_{8}.\end{eqnarray}$$
$$\begin{eqnarray}A_{1}\subset A_{2}\subset G_{2}\subset D_{4}\subset F_{4}\subset E_{6}\subset E_{7}\subset E_{8}.\end{eqnarray}$$
The penultimate row of the triangle is the one most relevant for this paper:
 $$\begin{eqnarray}\mathbf{G}_{m}\subset A_{1}\subset A_{1}^{3}\subset C_{3}\subset A_{5}\subset D_{6}\subset E_{7}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{G}_{m}\subset A_{1}\subset A_{1}^{3}\subset C_{3}\subset A_{5}\subset D_{6}\subset E_{7}.\end{eqnarray}$$
Each group in the triangle has a preferred representation. Many of the groups also have a preferred parabolic subgroup, obtained by taking the stabilizer of a highest line in the preferred representation. In row (B.1), the preferred representation is the adjoint representation, and the preferred parabolic subgroup is a Heisenberg parabolic. In row (B.2), the preferred representation is given by Freudenthal’s space
 $F\oplus J\oplus J\oplus F$
, where
$F\oplus J\oplus J\oplus F$
, where
![]() $J$
is a certain cubic Jordan algebra that corresponds to the group in question. The preferred parabolic subgroup is the stabilizer of a rank-one line in this space, which is a Siegel parabolic. So, the group
$J$
is a certain cubic Jordan algebra that corresponds to the group in question. The preferred parabolic subgroup is the stabilizer of a rank-one line in this space, which is a Siegel parabolic. So, the group
![]() $D_{6}$
in row (B.2) is the group
$D_{6}$
in row (B.2) is the group
![]() $\text{G}$
from the main body of the paper, its preferred representation being
$\text{G}$
from the main body of the paper, its preferred representation being
![]() $W$
and the preferred parabolic subgroup being the Siegel parabolic
$W$
and the preferred parabolic subgroup being the Siegel parabolic
![]() $P$
, the parabolic used to define the Eisenstein series in the integral representation.
$P$
, the parabolic used to define the Eisenstein series in the integral representation.
One can find many Rankin–Selberg integrals by applying the following procedure. Take two groups
 $H_{i}\subset H_{j}$
or
$H_{i}\subset H_{j}$
or
 $H_{j}\subset H_{i}$
in the same row. Take a cusp form
$H_{j}\subset H_{i}$
in the same row. Take a cusp form
![]() $\unicode[STIX]{x1D719}_{i}$
on
$\unicode[STIX]{x1D719}_{i}$
on
![]() $H_{i}(\mathbf{A})$
, and an Eisenstein series
$H_{i}(\mathbf{A})$
, and an Eisenstein series
 $E_{j}(g,s)$
corresponding to the preferred parabolic subgroup on
$E_{j}(g,s)$
corresponding to the preferred parabolic subgroup on
![]() $H_{j}(\mathbf{A})$
. Then one gets a global Rankin–Selberg convolution
$H_{j}(\mathbf{A})$
. Then one gets a global Rankin–Selberg convolution
 $$\begin{eqnarray}\int _{H_{i}(\mathbf{Q})\backslash H_{i}(\mathbf{A})}\unicode[STIX]{x1D719}_{i}(g)E_{j}(g,s)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{i}(\mathbf{Q})\backslash H_{i}(\mathbf{A})}\unicode[STIX]{x1D719}_{i}(g)E_{j}(g,s)\,dg\end{eqnarray}$$
if
 $H_{i}\subset H_{j}$
or
$H_{i}\subset H_{j}$
or
 $$\begin{eqnarray}\int _{H_{j}(\mathbf{Q})\backslash H_{j}(\mathbf{A})}\unicode[STIX]{x1D719}_{i}(g)E_{j}(g,s)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{H_{j}(\mathbf{Q})\backslash H_{j}(\mathbf{A})}\unicode[STIX]{x1D719}_{i}(g)E_{j}(g,s)\,dg\end{eqnarray}$$
if
 $H_{j}\subset H_{i}$
. Sometimes one must add in some additional unipotent integration to make the Rankin–Selberg convolution produce an
$H_{j}\subset H_{i}$
. Sometimes one must add in some additional unipotent integration to make the Rankin–Selberg convolution produce an
![]() $L$
-function. Of course, considering the inclusion
$L$
-function. Of course, considering the inclusion
 $C_{3}\subset D_{6}$
yields the integral in this paper, whereas the inclusion
$C_{3}\subset D_{6}$
yields the integral in this paper, whereas the inclusion
 $A_{1}^{3}\subset C_{3}$
yields the integral of [Reference Pollack and ShahPS15], if one puts the cusp form on
$A_{1}^{3}\subset C_{3}$
yields the integral of [Reference Pollack and ShahPS15], if one puts the cusp form on
![]() $C_{3}$
and the Eisenstein series on
$C_{3}$
and the Eisenstein series on
![]() $A_{1}^{3}$
. If one instead puts the cusp form on
$A_{1}^{3}$
. If one instead puts the cusp form on
![]() $A_{1}^{3}$
and the Eisenstein series on
$A_{1}^{3}$
and the Eisenstein series on
![]() $C_{3}$
, one gets the triple product
$C_{3}$
, one gets the triple product
![]() $L$
-function of Garrett [Reference GarrettGar87] and Piatetski-Shapiro and Rallis [Reference Piatetski-Shapiro and RallisPSR87]. The inclusion
$L$
-function of Garrett [Reference GarrettGar87] and Piatetski-Shapiro and Rallis [Reference Piatetski-Shapiro and RallisPSR87]. The inclusion
 $A_{1}\subset C_{3}$
yields the Whittaker integral of Bump and Ginzburg [Reference Bump and GinzburgBG92] for the Spin
$A_{1}\subset C_{3}$
yields the Whittaker integral of Bump and Ginzburg [Reference Bump and GinzburgBG92] for the Spin
![]() $L$
-function on
$L$
-function on
![]() $\operatorname{GSp}_{6}$
, except now one must add a unipotent group to the
$\operatorname{GSp}_{6}$
, except now one must add a unipotent group to the
![]() $A_{1}$
here.
$A_{1}$
here.
The integral of Furusawa for the degree-eight
![]() $L$
-function on
$L$
-function on
 $\operatorname{GSp}_{4}\times \operatorname{GU}(1,1)$
is not technically present in the row (B.2), but one can add it there, as follows. The groups, their preferred representations, and their preferred parabolic subgroups in this row all come from the Freudenthal construction. The Freudenthal construction can be made for a general cubic Jordan algebra
$\operatorname{GSp}_{4}\times \operatorname{GU}(1,1)$
is not technically present in the row (B.2), but one can add it there, as follows. The groups, their preferred representations, and their preferred parabolic subgroups in this row all come from the Freudenthal construction. The Freudenthal construction can be made for a general cubic Jordan algebra
![]() $J$
. For example, taking
$J$
. For example, taking
![]() $J$
to be
$J$
to be
![]() $H_{3}(B)$
yields the group
$H_{3}(B)$
yields the group
![]() $\text{G}$
of type
$\text{G}$
of type
![]() $D_{6}$
, whereas taking
$D_{6}$
, whereas taking
![]() $J$
to be
$J$
to be
 $\operatorname{Sym}_{3}(\mathbf{Q})$
, the
$\operatorname{Sym}_{3}(\mathbf{Q})$
, the
![]() $3\times 3$
symmetric matrices over
$3\times 3$
symmetric matrices over
![]() $\mathbf{Q}$
, yields the group
$\mathbf{Q}$
, yields the group
![]() $\operatorname{GSp}_{6}$
. If
$\operatorname{GSp}_{6}$
. If
![]() $E$
is a quadratic imaginary extension of
$E$
is a quadratic imaginary extension of
![]() $\mathbf{Q}$
, taking
$\mathbf{Q}$
, taking
 $J=H_{3}(E)$
, the
$J=H_{3}(E)$
, the
![]() $3\times 3$
Hermitian matrices over
$3\times 3$
Hermitian matrices over
![]() $E$
, yields the group
$E$
, yields the group
![]() $A_{5}$
from (B.2), which is essentially
$A_{5}$
from (B.2), which is essentially
 $\operatorname{GU}(3,3)$
. If one now takes
$\operatorname{GU}(3,3)$
. If one now takes
 $J=\mathbf{Q}\oplus \operatorname{Sym}_{2}(\mathbf{Q})$
, then the Freudenthal construction produces a group
$J=\mathbf{Q}\oplus \operatorname{Sym}_{2}(\mathbf{Q})$
, then the Freudenthal construction produces a group
![]() $H_{J}$
closely related to
$H_{J}$
closely related to
 $\operatorname{GU}(1,1)\times \operatorname{GSp}_{4}$
. Thus, one can think of the inclusion
$\operatorname{GU}(1,1)\times \operatorname{GSp}_{4}$
. Thus, one can think of the inclusion
 $H_{J}\subset \operatorname{GU}(3,3)$
as sitting in the row (B.2) as well, and this gives the integral of Furusawa.
$H_{J}\subset \operatorname{GU}(3,3)$
as sitting in the row (B.2) as well, and this gives the integral of Furusawa.
Amazingly, at least in the row (B.2), the magic triangle also helps to predict the
![]() $L$
-function realized by the integrals (B.3) and (B.4). The groups in row (B.2) appear as Levi subgroups of the preferred parabolic subgroup of a corresponding group from row (B.1). In the case of
$L$
-function realized by the integrals (B.3) and (B.4). The groups in row (B.2) appear as Levi subgroups of the preferred parabolic subgroup of a corresponding group from row (B.1). In the case of
![]() $C_{3}$
, the inclusion is into the Levi subgroup of the Heisenberg parabolic subgroup of the group
$C_{3}$
, the inclusion is into the Levi subgroup of the Heisenberg parabolic subgroup of the group
![]() $F_{4}$
from the exceptional series. The Spin
$F_{4}$
from the exceptional series. The Spin
![]() $L$
-function on
$L$
-function on
![]() $C_{3}$
appears in the constant term of a cuspidal Eisenstein series for this parabolic on
$C_{3}$
appears in the constant term of a cuspidal Eisenstein series for this parabolic on
![]() $F_{4}$
.
$F_{4}$
.
While we have mentioned some Rankin–Selberg integrals that seem to be connected to the row (B.2), one can find more Rankin–Selberg integrals in the literature that appear to be connected to this row, and to the other rows of the triangle. We also mention that the magic triangle appears both in the literature on dual pairs and the minimal representations of exceptional groups, see Rumelhart [Reference RumelhartRum97], and in recent works on arithmetic invariant theory, see Bhargava and Ho [Reference Bhargava and HoBH16].