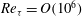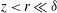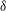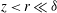1. Introduction
High-Reynolds-number wall turbulence is a commonly observed phenomenon and plays a central role in many engineering, environmental and geophysical flows. A robust feature of these flows, and one that is relied upon extensively for modelling purposes, is the logarithmic region (Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011; Jiménez Reference Jiménez2012), where the logarithmic law of the wall applies for the streamwise mean velocity. More recently, however, there is growing evidence also for logarithmic behaviour in the variance of both the streamwise (Hultmark Reference Hultmark2012; Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013) and spanwise (Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2013; Sillero, Jiménez & Moser Reference Sillero, Jiménez and Moser2013; Talluru et al. Reference Talluru, Baidya, Hutchins and Marusic2014) velocity fluctuations, and these observations are as predicted by the attached-eddy hypothesis of Townsend (Reference Townsend1976). Townsend’s hypothesis has become the basis of a physical model for wall turbulence (Perry & Chong Reference Perry and Chong1982; Perry, Henbest & Chong Reference Perry, Henbest and Chong1986; Perry & Marusic Reference Perry and Marusic1995; Marusic Reference Marusic2001), where the flow field in the logarithmic region is modelled by a hierarchy of spatially self-similar eddies, whose dimensions scale with their distance from the wall. Recently, Woodcock & Marusic (Reference Woodcock and Marusic2015) revisited the attached-eddy model and applied an extended form of Campbell’s theorem to derive expressions for the functional forms of all moments of the velocities, including cross-correlations. In this way, they were able to verify the earlier results of Townsend (Reference Townsend1976) and Perry & Chong (Reference Perry and Chong1982) for the mean flow and the variances, and the recent findings of Meneveau & Marusic (Reference Meneveau and Marusic2013) that all even-ordered moments of the streamwise velocity also exhibit a logarithmic dependence on the distance from the wall, once the Reynolds number is sufficiently high.
The distribution of energy across spatial scales prevalent in the logarithmic region is also of particular interest. This aspect has been studied extensively using both the one-dimensional power spectrum and the second-order structure function for the streamwise velocity. The
![]() $k^{-1}$
spectral law (where
$k^{-1}$
spectral law (where
![]() $k$
represents the streamwise wavenumber) has been predicted in the one-dimensional power spectrum of the streamwise velocity,
$k$
represents the streamwise wavenumber) has been predicted in the one-dimensional power spectrum of the streamwise velocity,
![]() ${\it\phi}_{uu}(k)$
, by various physical arguments (Högström, Hunt & Smedman Reference Högström, Hunt and Smedman2002; Davidson & Krogstad Reference Davidson and Krogstad2009, and others) and has been directly linked by Perry et al. (Reference Perry, Henbest and Chong1986) to the logarithmic formulation for the streamwise velocity variance by scaling arguments based on the attached-eddy hypothesis. While experimental support for a
${\it\phi}_{uu}(k)$
, by various physical arguments (Högström, Hunt & Smedman Reference Högström, Hunt and Smedman2002; Davidson & Krogstad Reference Davidson and Krogstad2009, and others) and has been directly linked by Perry et al. (Reference Perry, Henbest and Chong1986) to the logarithmic formulation for the streamwise velocity variance by scaling arguments based on the attached-eddy hypothesis. While experimental support for a
![]() $k^{-1}$
spectral law at sufficiently high Reynolds numbers has been reported by Nickels et al. (Reference Nickels, Marusic, Hafez and Chong2005), in general definitive experimental evidence has been elusive (Morrison et al.
Reference Morrison, McKeon, Jiang and Smits2004; Zhao & Smits Reference Zhao and Smits2007). Concurrently, increased support for a
$k^{-1}$
spectral law at sufficiently high Reynolds numbers has been reported by Nickels et al. (Reference Nickels, Marusic, Hafez and Chong2005), in general definitive experimental evidence has been elusive (Morrison et al.
Reference Morrison, McKeon, Jiang and Smits2004; Zhao & Smits Reference Zhao and Smits2007). Concurrently, increased support for a
![]() $k^{-1}$
spectral law has also been presented from recent numerical work as higher Reynolds numbers become realisable in simulations (Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2013; Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). Davidson, Nickels & Krogstad (Reference Davidson, Nickels and Krogstad2006b
) considered this issue in detail and concluded that the one-dimensional spectrum of streamwise velocity is not the ideal parameter to investigate scaling behaviour in the logarithmic region, due to measurement aliasing and other challenges, and proposed that structure functions provided a diagnostic that could be interpreted more clearly. Further, structure functions computed at higher orders provide additional statistical information, which is not available in a spectral space that only describes second-order statistics.
$k^{-1}$
spectral law has also been presented from recent numerical work as higher Reynolds numbers become realisable in simulations (Pirozzoli & Bernardini Reference Pirozzoli and Bernardini2013; Bernardini, Pirozzoli & Orlandi Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015). Davidson, Nickels & Krogstad (Reference Davidson, Nickels and Krogstad2006b
) considered this issue in detail and concluded that the one-dimensional spectrum of streamwise velocity is not the ideal parameter to investigate scaling behaviour in the logarithmic region, due to measurement aliasing and other challenges, and proposed that structure functions provided a diagnostic that could be interpreted more clearly. Further, structure functions computed at higher orders provide additional statistical information, which is not available in a spectral space that only describes second-order statistics.
Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) showed that the analogous counterpart to the
![]() $k^{-1}$
spectral law was a
$k^{-1}$
spectral law was a
![]() $\ln (r/z)$
law for the second-order structure function, where
$\ln (r/z)$
law for the second-order structure function, where
![]() $r$
is the spatial separation in the streamwise direction and
$r$
is the spatial separation in the streamwise direction and
![]() $z$
is the distance from the wall. Experimental evidence for a
$z$
is the distance from the wall. Experimental evidence for a
![]() $\ln (r/z)$
law for the second-order structure function was presented by Davidson and coworkers (Davidson, Krogstad & Nickels Reference Davidson, Krogstad and Nickels2006a
; Davidson et al.
Reference Davidson, Nickels and Krogstad2006b
; Davidson & Krogstad Reference Davidson and Krogstad2009). Their work shows that the
$\ln (r/z)$
law for the second-order structure function was presented by Davidson and coworkers (Davidson, Krogstad & Nickels Reference Davidson, Krogstad and Nickels2006a
; Davidson et al.
Reference Davidson, Nickels and Krogstad2006b
; Davidson & Krogstad Reference Davidson and Krogstad2009). Their work shows that the
![]() $\ln (r/z)$
law extends from the largest length scales that bound the Kolmogorov inertial subrange from above,
$\ln (r/z)$
law extends from the largest length scales that bound the Kolmogorov inertial subrange from above,
![]() $r\approx z$
(see Tennekes & Lumley Reference Tennekes and Lumley1972), up to the large scale contribution range associated with eddies that scale in the order of
$r\approx z$
(see Tennekes & Lumley Reference Tennekes and Lumley1972), up to the large scale contribution range associated with eddies that scale in the order of
![]() ${\it\delta}$
(boundary layer thickness). More recent studies using structure functions have shown universality in scaling behaviour using data from both smooth and rough boundary layers (Davidson & Krogstad Reference Davidson and Krogstad2014), closely following the expected behaviour based on models and outer layer similarity described in Perry & Li (Reference Perry and Li1990) and Schultz & Flack (Reference Schultz and Flack2005).
${\it\delta}$
(boundary layer thickness). More recent studies using structure functions have shown universality in scaling behaviour using data from both smooth and rough boundary layers (Davidson & Krogstad Reference Davidson and Krogstad2014), closely following the expected behaviour based on models and outer layer similarity described in Perry & Li (Reference Perry and Li1990) and Schultz & Flack (Reference Schultz and Flack2005).
At sufficiently high Reynolds numbers, one also expects an inertial subrange residing at scales that are larger than the dissipative range but smaller than those associated with the
![]() $k^{-1}$
spectral or
$k^{-1}$
spectral or
![]() $\ln (r/z)$
law. In this range, turbulence is expected to be locally isotropic, as described by Kolmogorov (Reference Kolmogorov1941), with
$\ln (r/z)$
law. In this range, turbulence is expected to be locally isotropic, as described by Kolmogorov (Reference Kolmogorov1941), with
![]() $k^{-5/3}$
and
$k^{-5/3}$
and
![]() $(r/z)^{2/3}$
scalings for the spectrum and second-order structure function respectively. The notion of universality provided great impetus for the study of small scales, which has led to a wide array of studies (reviewed by Sreenivasan & Antonia Reference Sreenivasan and Antonia1997) that extended the seminal work of Kolmogorov (Reference Kolmogorov1941). Of particular interest are the scaling exponents of the power-law behaviour observed in structure functions within the inertial subrange (Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1987; She & Leveque Reference She and Leveque1994). Subsequently, the influence of intermittency in small-scale turbulence has also gained attention in a range of studies, including wall-bounded turbulence (Benzi et al.
Reference Benzi, Amati, Casciola, Toschi and Piva1999; Toschi et al.
Reference Toschi, Amati, Succi, Benzi and Piva1999; Poggi, Porporato & Ridolfi Reference Poggi, Porporato and Ridolfi2003; Jacob et al.
Reference Jacob, Biferale, Iuso and Casciola2004, and others) and homogeneous shear flows (Gualtieri et al.
Reference Gualtieri, Casciola, Benzi, Amati and Piva2002; Casciola et al.
Reference Casciola, Gualtieri, Benzi and Piva2003, Reference Casciola, Gualtieri, Jacob and Piva2005), where focus is placed on improving intermittency models. Several of these studies have shown the benefits of using the
$(r/z)^{2/3}$
scalings for the spectrum and second-order structure function respectively. The notion of universality provided great impetus for the study of small scales, which has led to a wide array of studies (reviewed by Sreenivasan & Antonia Reference Sreenivasan and Antonia1997) that extended the seminal work of Kolmogorov (Reference Kolmogorov1941). Of particular interest are the scaling exponents of the power-law behaviour observed in structure functions within the inertial subrange (Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Meneveau & Sreenivasan Reference Meneveau and Sreenivasan1987; She & Leveque Reference She and Leveque1994). Subsequently, the influence of intermittency in small-scale turbulence has also gained attention in a range of studies, including wall-bounded turbulence (Benzi et al.
Reference Benzi, Amati, Casciola, Toschi and Piva1999; Toschi et al.
Reference Toschi, Amati, Succi, Benzi and Piva1999; Poggi, Porporato & Ridolfi Reference Poggi, Porporato and Ridolfi2003; Jacob et al.
Reference Jacob, Biferale, Iuso and Casciola2004, and others) and homogeneous shear flows (Gualtieri et al.
Reference Gualtieri, Casciola, Benzi, Amati and Piva2002; Casciola et al.
Reference Casciola, Gualtieri, Benzi and Piva2003, Reference Casciola, Gualtieri, Jacob and Piva2005), where focus is placed on improving intermittency models. Several of these studies have shown the benefits of using the
![]() $SO(3)$
decomposition to isolate isotropic and anisotropic effects to observe scaling behaviour in inhomogeneous and anisotropic turbulent flows. However, this approach requires spatial information and is more readily applicable to numerical simulation databases (Arad et al.
Reference Arad, Biferale, Mazzitelli and Procaccia1999).
$SO(3)$
decomposition to isolate isotropic and anisotropic effects to observe scaling behaviour in inhomogeneous and anisotropic turbulent flows. However, this approach requires spatial information and is more readily applicable to numerical simulation databases (Arad et al.
Reference Arad, Biferale, Mazzitelli and Procaccia1999).
Among the many studies that have considered structure functions in turbulent shear flows one notable result is the presence of a transition length scale (
![]() $L_{s}$
) (Hinze Reference Hinze1975; Toschi et al.
Reference Toschi, Amati, Succi, Benzi and Piva1999). At scales larger than
$L_{s}$
) (Hinze Reference Hinze1975; Toschi et al.
Reference Toschi, Amati, Succi, Benzi and Piva1999). At scales larger than
![]() $L_{s}$
shear is considered to be important, whereas at smaller scales shear is relatively unimportant. Consequently, one expects the structure function to scale differently on either side of
$L_{s}$
shear is considered to be important, whereas at smaller scales shear is relatively unimportant. Consequently, one expects the structure function to scale differently on either side of
![]() $L_{s}$
.
$L_{s}$
.
The results of Davidson and coworkers (Davidson et al.
Reference Davidson, Krogstad and Nickels2006a
,Reference Davidson, Nickels and Krogstad
b
; Davidson & Krogstad Reference Davidson and Krogstad2009) provide an interesting connection between the inertial subrange and the scales above
![]() $r/z\sim 1$
for the second-order structure functions. Insights relating exponents and prefactors in the respective scaling laws were obtained by properly matching the two behaviours at scales when
$r/z\sim 1$
for the second-order structure functions. Insights relating exponents and prefactors in the respective scaling laws were obtained by properly matching the two behaviours at scales when
![]() $r/z\sim 1$
.
$r/z\sim 1$
.
Here, we consider the abovementioned scaling behaviours using five experimental datasets in boundary layer flows that span several decades of Reynolds numbers (
![]() $Re$
). This significantly extends the range of scales available for the analysis and enables us to observe scaling laws unambiguously. Moreover, we also consider structure functions of higher orders. Using a uniquely large range of
$Re$
). This significantly extends the range of scales available for the analysis and enables us to observe scaling laws unambiguously. Moreover, we also consider structure functions of higher orders. Using a uniquely large range of
![]() $Re$
, the results provide experimental evidence that scaling laws for higher-order moments also lead to interesting connections between the two ranges that must meet at
$Re$
, the results provide experimental evidence that scaling laws for higher-order moments also lead to interesting connections between the two ranges that must meet at
![]() $r/z\sim 1$
. The experimental results are complemented with analysis that aims at connecting the results with those obtained in Meneveau & Marusic (Reference Meneveau and Marusic2013). Furthermore, we explore the predictive power of the attached-eddy hypothesis in studying the high-order structure functions in the
$r/z\sim 1$
. The experimental results are complemented with analysis that aims at connecting the results with those obtained in Meneveau & Marusic (Reference Meneveau and Marusic2013). Furthermore, we explore the predictive power of the attached-eddy hypothesis in studying the high-order structure functions in the
![]() $\ln (r/z)$
range of
$\ln (r/z)$
range of
![]() $r$
space.
$r$
space.
The paper is organised as follows. Section 2 provides a short summary of prior relevant results in scaling of second-order structure functions, higher-order moments of the velocity fluctuations and anomalous scaling (intermittency) in the inertial range. These prior results provide motivation for measurements of the structure functions over a vast range of scales and distances to the wall. Section 3 provides a description of the experimental datasets used. The main results obtained from each dataset for second- and higher-order streamwise structure functions are presented in § 4. These results are then followed in § 5 by a discussion of possible bridging relations connecting the higher-order moments of structure functions to those of the velocity fluctuations, generalising the results of Meneveau & Marusic (Reference Meneveau and Marusic2013). Then we show how the results in the
![]() $\ln (r/z)$
range are consistent with a physical model of the local large scales of the flow in § 5.2. There it is shown that the attached-eddy hypothesis may in fact be used to compute high-order moments of the structure functions, leading to concrete connections between the observed parameters of the scaling laws and those of the assumed distributions of eddies in the hierarchy. Section 6 discusses the universality of the coefficients computed for the scaling laws described in §§ 2 and 5, followed by a discussion on modelling the behaviour of the streamwise structure function based on established results from the inertial subrange.
$\ln (r/z)$
range are consistent with a physical model of the local large scales of the flow in § 5.2. There it is shown that the attached-eddy hypothesis may in fact be used to compute high-order moments of the structure functions, leading to concrete connections between the observed parameters of the scaling laws and those of the assumed distributions of eddies in the hierarchy. Section 6 discusses the universality of the coefficients computed for the scaling laws described in §§ 2 and 5, followed by a discussion on modelling the behaviour of the streamwise structure function based on established results from the inertial subrange.
Throughout this paper, the coordinate system
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
refers to the streamwise, spanwise and wall-normal directions respectively. The corresponding instantaneous streamwise, spanwise and wall-normal velocity fluctuations are represented by
$z$
refers to the streamwise, spanwise and wall-normal directions respectively. The corresponding instantaneous streamwise, spanwise and wall-normal velocity fluctuations are represented by
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
. Overbars and
$w$
. Overbars and
![]() $\langle \,\rangle$
indicate averaged quantities, and superscript and subscript
$\langle \,\rangle$
indicate averaged quantities, and superscript and subscript
![]() $+$
signs refer to normalisation by inner scales. For example, we use
$+$
signs refer to normalisation by inner scales. For example, we use
![]() $l^{+}=lU_{{\it\tau}}/{\it\nu}$
for length and
$l^{+}=lU_{{\it\tau}}/{\it\nu}$
for length and
![]() $u^{+}=u/U_{{\it\tau}}$
for velocity, where
$u^{+}=u/U_{{\it\tau}}$
for velocity, where
![]() $U_{{\it\tau}}$
is the mean friction velocity and
$U_{{\it\tau}}$
is the mean friction velocity and
![]() ${\it\nu}$
is the kinematic viscosity of the fluid.
${\it\nu}$
is the kinematic viscosity of the fluid.
2. Relevant details from prior works on structure functions and extensions
This section provides the relevant background on scaling laws for the streamwise structure functions in turbulent boundary layers. Here, we define the streamwise structure function following the common notation
where
![]() $r$
represents the spatial separation,
$r$
represents the spatial separation,
![]() $n$
is a positive integer indicating the moment order and
$n$
is a positive integer indicating the moment order and
![]() $\boldsymbol{i}$
is the unit vector in the streamwise direction. As summarised by Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
), the second-order structure functions in the logarithmic region of a turbulent boundary layer are postulated to have four regions. At the smallest length scales where
$\boldsymbol{i}$
is the unit vector in the streamwise direction. As summarised by Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
), the second-order structure functions in the logarithmic region of a turbulent boundary layer are postulated to have four regions. At the smallest length scales where
![]() $r\ll z$
, Kolmogorov scaling is prevalent. At the other extreme
$r\ll z$
, Kolmogorov scaling is prevalent. At the other extreme
![]() $r\gg {\it\delta}$
,
$r\gg {\it\delta}$
,
![]() $\langle {\rm\Delta}u^{2}\rangle$
is independent of
$\langle {\rm\Delta}u^{2}\rangle$
is independent of
![]() $r$
and asymptotes to twice the streamwise turbulence intensity
$r$
and asymptotes to twice the streamwise turbulence intensity
![]() $2\langle u^{2}\rangle$
. Here, we focus on the two regions in between. Nevertheless, a brief summary of the relevant scaling for each of the four regions follows.
$2\langle u^{2}\rangle$
. Here, we focus on the two regions in between. Nevertheless, a brief summary of the relevant scaling for each of the four regions follows.
2.1. Structure functions at dissipative scales
At the smallest scales (Kolmogorov scales), using a Taylor series expansion with the assumption of homogeneous isotropic turbulence at these scales (Frisch Reference Frisch1995) we expect a scaling behaviour of
![]() $\langle {\rm\Delta}u^{2}\rangle$
according to
$\langle {\rm\Delta}u^{2}\rangle$
according to
where
![]() ${\it\epsilon}$
denotes the dissipation rate. For the presented analysis we limit ourselves to the logarithmic region in wall-normal space of high Reynolds number turbulent boundary layers. Within this region, there is a near balance between the turbulent production (
${\it\epsilon}$
denotes the dissipation rate. For the presented analysis we limit ourselves to the logarithmic region in wall-normal space of high Reynolds number turbulent boundary layers. Within this region, there is a near balance between the turbulent production (
![]() $\mathscr{P}$
) and dissipation (
$\mathscr{P}$
) and dissipation (
![]() ${\it\epsilon}$
) rates (Tennekes & Lumley Reference Tennekes and Lumley1972; Townsend Reference Townsend1976, and others). Thus,
${\it\epsilon}$
) rates (Tennekes & Lumley Reference Tennekes and Lumley1972; Townsend Reference Townsend1976, and others). Thus,
where
![]() ${\it\kappa}$
is von Kármán’s constant. We note that Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) have explored deviations from this equilibrium assumption at lower
${\it\kappa}$
is von Kármán’s constant. We note that Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) have explored deviations from this equilibrium assumption at lower
![]() $Re$
. In wall-bounded turbulence at wall-normal locations within the logarithmic region (2.2) simplifies to
$Re$
. In wall-bounded turbulence at wall-normal locations within the logarithmic region (2.2) simplifies to
which holds at scales smaller than the Kolmogorov length,
![]() $0<r\lesssim {\it\eta}=({\it\nu}^{3}/{\it\epsilon})^{1/4}$
, i.e.
$0<r\lesssim {\it\eta}=({\it\nu}^{3}/{\it\epsilon})^{1/4}$
, i.e.
![]() $r/z\lesssim z_{+}^{-3/4}{\it\kappa}^{1/4}$
. A Taylor series expansion also leads to integer scaling exponents for higher-order structure functions (
$r/z\lesssim z_{+}^{-3/4}{\it\kappa}^{1/4}$
. A Taylor series expansion also leads to integer scaling exponents for higher-order structure functions (
![]() $\langle {\rm\Delta}u^{n}\rangle \sim r^{n}$
) in the dissipative range (Nelkin Reference Nelkin1990).
$\langle {\rm\Delta}u^{n}\rangle \sim r^{n}$
) in the dissipative range (Nelkin Reference Nelkin1990).
2.2. Structure functions in the inertial subrange
 ${\it\eta}\ll r\ll z$
${\it\eta}\ll r\ll z$
At these scales we expect scaling behaviour to be representative of local isotropy. Following Anselmet et al. (Reference Anselmet, Gagne, Hopfinger and Antonia1984) the scaling in this inertial subrange can be expressed as
where
![]() ${\it\xi}_{n}$
is the anomalous scaling exponent and
${\it\xi}_{n}$
is the anomalous scaling exponent and
![]() $\ell$
is a length scale. The Kolmogorov 1941 theory predicts
$\ell$
is a length scale. The Kolmogorov 1941 theory predicts
![]() ${\it\xi}_{2}=2/3$
for the second-order structure function as well as
${\it\xi}_{2}=2/3$
for the second-order structure function as well as
![]() ${\it\xi}_{n}=n/3$
for higher-order moments. Data instead show anomalous scaling with
${\it\xi}_{n}=n/3$
for higher-order moments. Data instead show anomalous scaling with
![]() ${\it\xi}_{n}<n/3$
for
${\it\xi}_{n}<n/3$
for
![]() $n>3$
(Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). The trends can be fitted quite well empirically using the log-Poisson model of She & Leveque (Reference She and Leveque1994),
$n>3$
(Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). The trends can be fitted quite well empirically using the log-Poisson model of She & Leveque (Reference She and Leveque1994),
or the
![]() $p$
-model of Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1987),
$p$
-model of Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1987),
Thus, for even moments
![]() $n=(2,4,6,8,10)$
, we obtain from She & Leveque (Reference She and Leveque1994)
$n=(2,4,6,8,10)$
, we obtain from She & Leveque (Reference She and Leveque1994)
![]() ${\it\xi}_{n}=(0.6959,1.2797,1.7778,2.2105,2.5934)$
, and
${\it\xi}_{n}=(0.6959,1.2797,1.7778,2.2105,2.5934)$
, and
![]() ${\it\xi}_{n}=(0.6937,1.2822,1.7859,2.2289,2.6321)$
for the
${\it\xi}_{n}=(0.6937,1.2822,1.7859,2.2289,2.6321)$
for the
![]() $p$
-model, essentially the same within experimental accuracy. For concordance with recent work on even moments, we shall set
$p$
-model, essentially the same within experimental accuracy. For concordance with recent work on even moments, we shall set
![]() $n=2p$
below and only focus on even moments
$n=2p$
below and only focus on even moments
![]() $2p$
. Moreover, for wall-bounded flow, using (2.3) and setting
$2p$
. Moreover, for wall-bounded flow, using (2.3) and setting
![]() $\ell =z$
(the distance to the wall), in non-dimensional form we obtain
$\ell =z$
(the distance to the wall), in non-dimensional form we obtain
with
![]() $M_{p}=C_{2p}^{1/p}{\it\kappa}^{-2/3}$
. For wall-bounded flows, in the logarithmic layer such scaling is expected to hold in the range
$M_{p}=C_{2p}^{1/p}{\it\kappa}^{-2/3}$
. For wall-bounded flows, in the logarithmic layer such scaling is expected to hold in the range
![]() ${\it\eta}\ll r\ll z$
, or
${\it\eta}\ll r\ll z$
, or
![]() $z_{+}^{-3/4}{\it\kappa}^{1/4}\ll r/z\ll 1$
.
$z_{+}^{-3/4}{\it\kappa}^{1/4}\ll r/z\ll 1$
.
2.3. Second-order structure functions at scales
 $z<r\ll {\it\delta}$
$z<r\ll {\it\delta}$
Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) argued that
![]() $\langle {\rm\Delta}u^{2}\rangle$
can be considered as the cumulative energy of eddies of size
$\langle {\rm\Delta}u^{2}\rangle$
can be considered as the cumulative energy of eddies of size
![]() $r$
and less. They postulated that at scales
$r$
and less. They postulated that at scales
![]() $r>z$
,
$r>z$
,
![]() $\langle {\rm\Delta}u^{2}\rangle$
will be dominated by inertial-scale eddies whose heights are roughly between
$\langle {\rm\Delta}u^{2}\rangle$
will be dominated by inertial-scale eddies whose heights are roughly between
![]() $z$
and
$z$
and
![]() $r$
, with kinetic energy of order
$r$
, with kinetic energy of order
![]() $U_{{\it\tau}}^{2}$
. Accordingly, considering
$U_{{\it\tau}}^{2}$
. Accordingly, considering
![]() $\text{d}\langle {\rm\Delta}u^{2}\rangle /\text{d}r$
as an energy density Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) proposed that
$\text{d}\langle {\rm\Delta}u^{2}\rangle /\text{d}r$
as an energy density Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) proposed that
![]() $r\text{d}\langle {\rm\Delta}u^{2}\rangle /\text{d}r$
is a constant proportional to
$r\text{d}\langle {\rm\Delta}u^{2}\rangle /\text{d}r$
is a constant proportional to
![]() $U_{{\it\tau}}^{2}$
. When integrated, a logarithmic law of the form
$U_{{\it\tau}}^{2}$
. When integrated, a logarithmic law of the form
is obtained. The coefficients
![]() $D_{1}$
and
$D_{1}$
and
![]() $E_{1}$
were evaluated by Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) based on modelling assumptions and moderate Reynolds number data.
$E_{1}$
were evaluated by Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
) based on modelling assumptions and moderate Reynolds number data.
In a more detailed study, Davidson et al. (Reference Davidson, Krogstad and Nickels2006a
) proposed that
![]() $r$
should be normalised by the length scale
$r$
should be normalised by the length scale
![]() $U_{{\it\tau}}^{3}/{\it\epsilon}$
rather than
$U_{{\it\tau}}^{3}/{\it\epsilon}$
rather than
![]() $z$
in (2.9). It is worth highlighting that
$z$
in (2.9). It is worth highlighting that
![]() $U_{{\it\tau}}^{3}/{\it\epsilon}$
is equivalent to scaling with
$U_{{\it\tau}}^{3}/{\it\epsilon}$
is equivalent to scaling with
![]() $z$
(after substitution for
$z$
(after substitution for
![]() ${\it\epsilon}$
using (2.3)), valid at high Reynolds numbers assuming that equilibrium holds. Therefore, they proposed that (2.9) should be replaced by
${\it\epsilon}$
using (2.3)), valid at high Reynolds numbers assuming that equilibrium holds. Therefore, they proposed that (2.9) should be replaced by
where
![]() $E_{1}^{\ast }$
is a constant of order unity. Based on their modelling, Davidson & Krogstad (Reference Davidson and Krogstad2009) postulated that
$E_{1}^{\ast }$
is a constant of order unity. Based on their modelling, Davidson & Krogstad (Reference Davidson and Krogstad2009) postulated that
![]() $E_{1}^{\ast }$
and
$E_{1}^{\ast }$
and
![]() $D_{1}$
are universal constants in turbulent boundary layers. Indeed, Davidson et al. (Reference Davidson, Krogstad and Nickels2006a
) showed an improvement when using (2.10) (i.e. using
$D_{1}$
are universal constants in turbulent boundary layers. Indeed, Davidson et al. (Reference Davidson, Krogstad and Nickels2006a
) showed an improvement when using (2.10) (i.e. using
![]() $U_{{\it\tau}}^{3}/{\it\epsilon}$
to normalise
$U_{{\it\tau}}^{3}/{\it\epsilon}$
to normalise
![]() $r$
rather than
$r$
rather than
![]() $z$
). This can be attributed to the finite
$z$
). This can be attributed to the finite
![]() $Re$
range studied. Davidson & Krogstad (Reference Davidson and Krogstad2014) further considered these issues for smooth and rough wall flows for structure functions up to sixth order.
$Re$
range studied. Davidson & Krogstad (Reference Davidson and Krogstad2014) further considered these issues for smooth and rough wall flows for structure functions up to sixth order.
We note that for simplicity in the presentation hereafter, the range
![]() $z<r\ll {\it\delta}$
within the inertial region of structure functions will be referred to as the ‘
$z<r\ll {\it\delta}$
within the inertial region of structure functions will be referred to as the ‘
![]() $\ln (r/z)$
region’, following Davidson and coworkers.
$\ln (r/z)$
region’, following Davidson and coworkers.
2.4. Second- and higher-order moments of streamwise velocity
As summarised in the introduction, there is growing evidence of logarithmic behaviour in the variance of the streamwise velocity fluctuations (Hultmark Reference Hultmark2012; Marusic et al. Reference Marusic, Monty, Hultmark and Smits2013), and a similar behaviour in high-order moments has been observed (Meneveau & Marusic Reference Meneveau and Marusic2013). For arbitrary even-order moments, this can be written according to
where for
![]() $p=1$
the scaling of the variance involves the ‘Townsend–Perry constant’
$p=1$
the scaling of the variance involves the ‘Townsend–Perry constant’
![]() $A_{1}\approx 1.25$
. For Gaussian statistics, Meneveau & Marusic (Reference Meneveau and Marusic2013) pointed out that
$A_{1}\approx 1.25$
. For Gaussian statistics, Meneveau & Marusic (Reference Meneveau and Marusic2013) pointed out that
![]() $A_{p}=[(2p-1)!!]^{1/p}A_{1}$
for higher-order even moments. They found that the values of
$A_{p}=[(2p-1)!!]^{1/p}A_{1}$
for higher-order even moments. They found that the values of
![]() $A_{p}$
for
$A_{p}$
for
![]() $p>1$
measured from experimental data display sub-Gaussian behaviour, i.e.
$p>1$
measured from experimental data display sub-Gaussian behaviour, i.e.
![]() $A_{p}<[(2p-1)!!]^{1/p}A_{1}$
. Such results have also been recently obtained in large-eddy simulations by Stevens, Wilczek & Meneveau (Reference Stevens, Wilczek and Meneveau2014). Preliminary discussions are also presented for the spanwise and wall-normal velocity components as all velocity components are available from the LES datasets.
$A_{p}<[(2p-1)!!]^{1/p}A_{1}$
. Such results have also been recently obtained in large-eddy simulations by Stevens, Wilczek & Meneveau (Reference Stevens, Wilczek and Meneveau2014). Preliminary discussions are also presented for the spanwise and wall-normal velocity components as all velocity components are available from the LES datasets.
It can be noted (Davidson & Krogstad Reference Davidson and Krogstad2009) that (2.11) and (2.9) (evaluated at
![]() $r={\it\delta}$
) display a dependence on height
$r={\it\delta}$
) display a dependence on height
![]() $z$
that is consistent with the expected limiting behaviour when
$z$
that is consistent with the expected limiting behaviour when
![]() $r\gg {\it\delta}$
,
$r\gg {\it\delta}$
,
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle =2\langle u_{+}^{2}\rangle$
, with
$\langle {\rm\Delta}u_{+}^{2}\rangle =2\langle u_{+}^{2}\rangle$
, with
![]() $D_{1}=2A_{1}$
.
$D_{1}=2A_{1}$
.
2.5. Postulate for higher-order structure functions at scales
 $z<r\ll {\it\delta}$
$z<r\ll {\it\delta}$
Having considered the points summarised in the preceding sections, we now consider higher-order structure functions in the range
![]() $z<r\ll {\it\delta}$
(the
$z<r\ll {\it\delta}$
(the
![]() $\ln (r/z)$
region). If in that range the variance of the velocity increment follows a logarithmic law as in (2.9), then following the same arguments as Meneveau & Marusic (Reference Meneveau and Marusic2013) for higher-order moments of velocity fluctuations, one can postulate the following scaling for higher-order structure functions:
$\ln (r/z)$
region). If in that range the variance of the velocity increment follows a logarithmic law as in (2.9), then following the same arguments as Meneveau & Marusic (Reference Meneveau and Marusic2013) for higher-order moments of velocity fluctuations, one can postulate the following scaling for higher-order structure functions:
In particular, when
![]() $r={\it\delta}$
, one can show (see § 5.1 for more details) that this expression recovers the limiting behaviour consistent with (2.11) for the
$r={\it\delta}$
, one can show (see § 5.1 for more details) that this expression recovers the limiting behaviour consistent with (2.11) for the
![]() $z$
dependence of the logarithmic behaviour of high-order moments at
$z$
dependence of the logarithmic behaviour of high-order moments at
![]() $r\gg {\it\delta}$
. Further motivation for expecting a logarithmic behaviour of the high-order structure functions can be provided by model calculations based on the attached-eddy hypothesis. As shown in § 5.2, the spatial structure that arises from a superposition of attached eddies can be used to compute velocity increments, and their moments in that range lead directly to logarithmic scaling.
$r\gg {\it\delta}$
. Further motivation for expecting a logarithmic behaviour of the high-order structure functions can be provided by model calculations based on the attached-eddy hypothesis. As shown in § 5.2, the spatial structure that arises from a superposition of attached eddies can be used to compute velocity increments, and their moments in that range lead directly to logarithmic scaling.
However, first, in the next sections we present empirical evidence for (2.12) based on the experimental data. The analysis of data is presented in § 4.2. Further derivations and the modelling of higher-order structure functions based on the attached-eddy hypothesis are subsequently presented in § 5.
3. The experimental data
The present study utilises five experimental databases, with key parameters provided in table 1. For the present analysis we have chosen databases that have friction Reynolds numbers that exceed
![]() $Re_{{\it\tau}}\gtrsim 5000$
. This threshold satisfies multiple criteria to consider a boundary layer to be a high Reynolds number flow, which are summarised in a recent review article by Smits et al. (Reference Smits, McKeon and Marusic2011). These criteria include sufficient scale separation to decouple the viscous and energetic scales (McKeon & Morrison Reference McKeon and Morrison2007), a constant wake factor (Coles Reference Coles1962) and over a decade of logarithmic velocity variation in
$Re_{{\it\tau}}\gtrsim 5000$
. This threshold satisfies multiple criteria to consider a boundary layer to be a high Reynolds number flow, which are summarised in a recent review article by Smits et al. (Reference Smits, McKeon and Marusic2011). These criteria include sufficient scale separation to decouple the viscous and energetic scales (McKeon & Morrison Reference McKeon and Morrison2007), a constant wake factor (Coles Reference Coles1962) and over a decade of logarithmic velocity variation in
![]() $z^{+}$
, to name a few. Four datasets were acquired from the High Reynolds Number Boundary Layer Wind Tunnel (HRNBLWT) at the University of Melbourne. This facility has a large working section of 27 m in length, with a cross-sectional area of approximately
$z^{+}$
, to name a few. Four datasets were acquired from the High Reynolds Number Boundary Layer Wind Tunnel (HRNBLWT) at the University of Melbourne. This facility has a large working section of 27 m in length, with a cross-sectional area of approximately
![]() $2~\text{m}\times 1~\text{m}$
. The long working section provides a long development length, leading to a boundary layer thickness of approximately 0.35 m at the end of the working section, and thus presents less acute spatial resolution issues. Further details of the facility are provided in Nickels et al. (Reference Nickels, Marusic, Hafez and Chong2005). The two single-wire hot-wire anemometry measurements from this facility are at different streamwise positions and free stream velocities, but are more or less comparable otherwise. Both use
$2~\text{m}\times 1~\text{m}$
. The long working section provides a long development length, leading to a boundary layer thickness of approximately 0.35 m at the end of the working section, and thus presents less acute spatial resolution issues. Further details of the facility are provided in Nickels et al. (Reference Nickels, Marusic, Hafez and Chong2005). The two single-wire hot-wire anemometry measurements from this facility are at different streamwise positions and free stream velocities, but are more or less comparable otherwise. Both use
![]() $2.5~{\rm\mu}\text{m}$
diameter Wollaston wires operated by an in-house constant-temperature anemometer (MUCTA). The spatial resolution in viscous units is shown in table 1 and is considered to be sufficient to resolve the turbulence intensity accurately within the logarithmic region wall-normal locations considered in this study based on the guidelines laid out by Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009). The other datasets from the Melbourne wind tunnel were obtained from a planar PIV measurement using a unique experimental set-up with multiple cameras to obtain a large field of view (streamwise extent
$2.5~{\rm\mu}\text{m}$
diameter Wollaston wires operated by an in-house constant-temperature anemometer (MUCTA). The spatial resolution in viscous units is shown in table 1 and is considered to be sufficient to resolve the turbulence intensity accurately within the logarithmic region wall-normal locations considered in this study based on the guidelines laid out by Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009). The other datasets from the Melbourne wind tunnel were obtained from a planar PIV measurement using a unique experimental set-up with multiple cameras to obtain a large field of view (streamwise extent
![]() ${>}2{\it\delta}$
) with targeted spatial resolution closer to the wall where it is most critical (de Silva et al.
Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). The highly magnified field of view (high-mag FOV) targeted at the near-wall region is ideally suited for this analysis, and provides spatial information across the sublayer and lower region of the logarithmic layer with a spatial resolution of a few viscous length scales. Meanwhile, the large-FOV PIV provides direct spatial information for a large streamwise extent of the order
${>}2{\it\delta}$
) with targeted spatial resolution closer to the wall where it is most critical (de Silva et al.
Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). The highly magnified field of view (high-mag FOV) targeted at the near-wall region is ideally suited for this analysis, and provides spatial information across the sublayer and lower region of the logarithmic layer with a spatial resolution of a few viscous length scales. Meanwhile, the large-FOV PIV provides direct spatial information for a large streamwise extent of the order
![]() ${\it\delta}$
.
${\it\delta}$
.
The final dataset to be considered was acquired using hot-wire anemometry in the surface layer of the atmospheric boundary layer at the Surface Layer Turbulence and Environmental Test Facility (SLTEST) located at the Utah salt flats (Kunkel & Marusic Reference Kunkel and Marusic2006). The measurements involved a vertical array of ten
![]() $2.5~{\rm\mu}\text{m}$
diameter platinum-coated tungsten wires mounted from
$2.5~{\rm\mu}\text{m}$
diameter platinum-coated tungsten wires mounted from
![]() $z=0.005{-}2~\text{m}$
(spaced logarithmically in
$z=0.005{-}2~\text{m}$
(spaced logarithmically in
![]() $z$
), The placement of the wires was such that a large proportion of the velocity signals obtained were well within the logarithmic region of the flow. This dataset proved valuable for this work due to the significantly higher Reynolds number of the atmospheric boundary layer compared with laboratory experiments. Further details on all measurements can be found in their respective publications.
$z$
), The placement of the wires was such that a large proportion of the velocity signals obtained were well within the logarithmic region of the flow. This dataset proved valuable for this work due to the significantly higher Reynolds number of the atmospheric boundary layer compared with laboratory experiments. Further details on all measurements can be found in their respective publications.
Table 1. Summary of experiments.

For consistency, the friction velocity for the dataset from Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) was recomputed using the composite velocity profile of Chauhan, Monkewitz & Nagib (Reference Chauhan, Monkewitz and Nagib2009) with constants
![]() ${\it\kappa}=0.384$
and
${\it\kappa}=0.384$
and
![]() $A=4.17$
. Similarly, the same constants were used for the atmospheric boundary layer dataset of Kunkel & Marusic (Reference Kunkel and Marusic2006). However, since velocity signals are only available within the logarithmic region for this dataset, a simple modified Clauser chart fit was employed using the same log-law constants rather than a composite velocity profile.
$A=4.17$
. Similarly, the same constants were used for the atmospheric boundary layer dataset of Kunkel & Marusic (Reference Kunkel and Marusic2006). However, since velocity signals are only available within the logarithmic region for this dataset, a simple modified Clauser chart fit was employed using the same log-law constants rather than a composite velocity profile.
For the PIV measurement typically the interrogation window size dictates the spatial resolution. However, PIV is usually impacted by experimental noise to a higher degree than its hot-wire counterpart. The influence of noise on turbulence intensity statistics has been studied previously by drawing comparisons between PIV datasets and hot-wire/DNS datasets to determine the noise floor for PIV measurements (Atkinson et al.
Reference Atkinson, Buchmann, Amili and Soria2013). Following a similar approach, we selected the smallest separation
![]() $r$
to compute structure functions such that it was above the noise floor for each PIV measurement. Here the cutoff was chosen based on a direct comparison with a hot-wire dataset at a comparable Reynolds number.
$r$
to compute structure functions such that it was above the noise floor for each PIV measurement. Here the cutoff was chosen based on a direct comparison with a hot-wire dataset at a comparable Reynolds number.
As a final note, prior to proceeding with computing the higher-order moments of the streamwise structure function, the degree of convergence at higher moments needs to be considered. To assess the degree of convergence following the approach described in Meneveau & Marusic (Reference Meneveau and Marusic2013) the pre-multiplied probability density function for velocity fluctuations
![]() ${\rm\Delta}u_{+}^{2p}P({\rm\Delta}u_{+})$
was computed. The results are shown in figure 1, where (a) corresponds to a hot-wire dataset of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) and (b) represents the PIV dataset of de Silva et al. (Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). For the hot-wire dataset acceptable convergence is observed up to
${\rm\Delta}u_{+}^{2p}P({\rm\Delta}u_{+})$
was computed. The results are shown in figure 1, where (a) corresponds to a hot-wire dataset of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) and (b) represents the PIV dataset of de Silva et al. (Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). For the hot-wire dataset acceptable convergence is observed up to
![]() $2p=10$
in the sense that the area under the curve seems to be captured well with the amount of data available. Conversely, the PIV dataset only shows good convergence up to
$2p=10$
in the sense that the area under the curve seems to be captured well with the amount of data available. Conversely, the PIV dataset only shows good convergence up to
![]() $2p=6$
, as one may expect due to the significantly lower number of ensembles available (
$2p=6$
, as one may expect due to the significantly lower number of ensembles available (
![]() ${\approx}6\times 10^{6}$
for the hot-wire signal of Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009 and
${\approx}6\times 10^{6}$
for the hot-wire signal of Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009 and
![]() ${\approx}1\times 10^{6}$
after considering all captured large-FOV PIV frames of de Silva et al.
Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). We note that similar results are obtained for the other datasets employed, where all hot-wire datasets utilised show reasonable convergence up to
${\approx}1\times 10^{6}$
after considering all captured large-FOV PIV frames of de Silva et al.
Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). We note that similar results are obtained for the other datasets employed, where all hot-wire datasets utilised show reasonable convergence up to
![]() $2p=10$
and the high-mag FOV PIV shows a similar degree of convergence to the large-FOV PIV up to
$2p=10$
and the high-mag FOV PIV shows a similar degree of convergence to the large-FOV PIV up to
![]() $2p=6$
. Therefore, for the subsequent analysis results from the PIV datasets at
$2p=6$
. Therefore, for the subsequent analysis results from the PIV datasets at
![]() $2p>6$
should be considered with due caution.
$2p>6$
should be considered with due caution.

Figure 1. Premultiplied probability density function of
![]() ${\rm\Delta}u$
at
${\rm\Delta}u$
at
![]() $r\approx z^{+}$
, where
$r\approx z^{+}$
, where
![]() $z^{+}\approx 800$
. Both measurements were made in the HRNBLWT. (a) Hot-wire data of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009), (b) large-FOV PIV of de Silva et al. (Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). The moments
$z^{+}\approx 800$
. Both measurements were made in the HRNBLWT. (a) Hot-wire data of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009), (b) large-FOV PIV of de Silva et al. (Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). The moments
![]() $2p=2$
,
$2p=2$
,
![]() $6$
and
$6$
and
![]() $10$
are represented by ○, ▫ and ▵ respectively. The curves are separated by an arbitrary factor
$10$
are represented by ○, ▫ and ▵ respectively. The curves are separated by an arbitrary factor
![]() $K_{p}$
for clarity.
$K_{p}$
for clarity.
4. Experimental results
In this section we present results for the structure function of the streamwise velocity across all datasets considered. Here, we place emphasis mainly on the ranges
![]() ${\it\eta}\ll r\ll z$
and
${\it\eta}\ll r\ll z$
and
![]() $z<r\ll {\it\delta}$
to investigate the appropriate scaling behaviour. It is noted that the high-mag PIV from the HRNBLWT facility has adequate spatial resolution and streamwise extent to accommodate the inertial subrange (
$z<r\ll {\it\delta}$
to investigate the appropriate scaling behaviour. It is noted that the high-mag PIV from the HRNBLWT facility has adequate spatial resolution and streamwise extent to accommodate the inertial subrange (
![]() ${\it\eta}\ll r\ll z$
), but does not provide sufficient spatial information for the
${\it\eta}\ll r\ll z$
), but does not provide sufficient spatial information for the
![]() $\ln (r/z)$
range (
$\ln (r/z)$
range (
![]() $z<r\ll {\it\delta}$
). However, the high-mag and large-FOV PIV datasets have been measured simultaneously, and thus the large-FOV PIV dataset, with a spatial extent of the order of
$z<r\ll {\it\delta}$
). However, the high-mag and large-FOV PIV datasets have been measured simultaneously, and thus the large-FOV PIV dataset, with a spatial extent of the order of
![]() ${\it\delta}$
(de Silva et al.
Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014), provides the results in the range
${\it\delta}$
(de Silva et al.
Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014), provides the results in the range
![]() $z<r\ll {\it\delta}$
. The PIV data also provide direct spatial information without the need to invoke Taylor’s hypothesis, as required for the hot-wire datasets. When Taylor’s hypothesis is used in this paper, the convection velocity is taken to be the local mean velocity.
$z<r\ll {\it\delta}$
. The PIV data also provide direct spatial information without the need to invoke Taylor’s hypothesis, as required for the hot-wire datasets. When Taylor’s hypothesis is used in this paper, the convection velocity is taken to be the local mean velocity.
4.1. Scaling of the second-order structure function and influence of the wall-normal location
It is valuable to consider how the second-order structure function varies with both the wall-normal position and the spatial separation, and an attempt to illustrate this is shown in figure 2. Here, a three-dimensional view of
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle$
is presented at all measurement locations across the boundary layer height for the hot-wire dataset from Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) at
$\langle {\rm\Delta}u_{+}^{2}\rangle$
is presented at all measurement locations across the boundary layer height for the hot-wire dataset from Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) at
![]() $Re_{{\it\tau}}=19\,000$
with 50 wall-normal locations. The region highlighted in green on the surface formed from these profiles denotes the inertial scaling region where a
$Re_{{\it\tau}}=19\,000$
with 50 wall-normal locations. The region highlighted in green on the surface formed from these profiles denotes the inertial scaling region where a
![]() $\text{ln}(r/z)$
law is observed. Further, the presented three-dimensional surface provides a visual representation of the relationship between the linear–log region observed in
$\text{ln}(r/z)$
law is observed. Further, the presented three-dimensional surface provides a visual representation of the relationship between the linear–log region observed in
![]() $2\langle u_{+}^{2}\rangle$
(● symbols) and the
$2\langle u_{+}^{2}\rangle$
(● symbols) and the
![]() $\text{ln}(r/z)$
law in
$\text{ln}(r/z)$
law in
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle$
with the same multiplicative constant
$\langle {\rm\Delta}u_{+}^{2}\rangle$
with the same multiplicative constant
![]() $A_{1}$
(for
$A_{1}$
(for
![]() $p=1$
; (2.11)).
$p=1$
; (2.11)).

Figure 2. Three-dimensional surface generated using profiles of
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
$\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
![]() $r/z$
at all wall-normal locations from the hot-wire dataset of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) at
$r/z$
at all wall-normal locations from the hot-wire dataset of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) at
![]() $Re_{{\it\tau}}\approx 19\,000$
. The ● symbols correspond to
$Re_{{\it\tau}}\approx 19\,000$
. The ● symbols correspond to
![]() $2\overline{u^{2}}$
at each wall-normal location. The green shaded region corresponds to where a
$2\overline{u^{2}}$
at each wall-normal location. The green shaded region corresponds to where a
![]() $\ln (r/z)$
law is expected at wall-normal locations within the logarithmic region, highlighted by the darker contours. The indicated slopes are detailed further in § 6.
$\ln (r/z)$
law is expected at wall-normal locations within the logarithmic region, highlighted by the darker contours. The indicated slopes are detailed further in § 6.

Figure 3. (a) A plot of
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
$\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
![]() $r/z$
from hot-wire data at
$r/z$
from hot-wire data at
![]() $Re_{{\it\tau}}=19\,000$
of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009). Wall-normal locations: ▵,
$Re_{{\it\tau}}=19\,000$
of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009). Wall-normal locations: ▵,
![]() $z^{+}\approx 400$
; ▹, 700; ▫, 1000; ◃, 1900. The locations are selected to be within the logarithmic region. (b) A plot of
$z^{+}\approx 400$
; ▹, 700; ▫, 1000; ◃, 1900. The locations are selected to be within the logarithmic region. (b) A plot of
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
$\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
![]() $r/z$
after applying the correction outlined in (2.10) following Davidson et al. (Reference Davidson, Krogstad and Nickels2006a
). The solid lines correspond to formulations based on (2.9) and (2.10) in (a) and (b) respectively.
$r/z$
after applying the correction outlined in (2.10) following Davidson et al. (Reference Davidson, Krogstad and Nickels2006a
). The solid lines correspond to formulations based on (2.9) and (2.10) in (a) and (b) respectively.
In the following we will focus primarily on data from within the logarithmic region, which we take to be nominally within the range
![]() $3\sqrt{Re_{{\it\tau}}}\lesssim z^{+}\lesssim 0.15Re_{{\it\tau}}$
following recent observations using high Reynolds number datasets (Klewicki, Fife & Wei Reference Klewicki, Fife and Wei2009; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013; Chin et al.
Reference Chin, Philip, Klewicki, Ooi and Marusic2014). The two thicker, dark grey lines (red online) shown in figure 2 demarcate this region. The results in figure 2 indicate good support for (2.9), where
$3\sqrt{Re_{{\it\tau}}}\lesssim z^{+}\lesssim 0.15Re_{{\it\tau}}$
following recent observations using high Reynolds number datasets (Klewicki, Fife & Wei Reference Klewicki, Fife and Wei2009; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013; Chin et al.
Reference Chin, Philip, Klewicki, Ooi and Marusic2014). The two thicker, dark grey lines (red online) shown in figure 2 demarcate this region. The results in figure 2 indicate good support for (2.9), where
![]() $z$
is used as the normalising length scale. It is worthwhile to consider whether the refined formulation (2.10) of Davidson et al. (Reference Davidson, Krogstad and Nickels2006a
) is required at higher Reynolds numbers. Figure 3 shows a comparison between formulations (2.9) and (2.10) for results within the logarithmic region for the same data as in figure 2. The results show that inclusion of the extra term involving production and dissipation slightly improves the collapse of the data in the inertial range (
$z$
is used as the normalising length scale. It is worthwhile to consider whether the refined formulation (2.10) of Davidson et al. (Reference Davidson, Krogstad and Nickels2006a
) is required at higher Reynolds numbers. Figure 3 shows a comparison between formulations (2.9) and (2.10) for results within the logarithmic region for the same data as in figure 2. The results show that inclusion of the extra term involving production and dissipation slightly improves the collapse of the data in the inertial range (
![]() $z<r\ll {\it\delta}$
), although its effect is probably not required at this Reynolds number. This is primarily due to the fact that the turbulent production and dissipation rates are nominally equal in the logarithmic region at sufficiently high Reynolds numbers (Tennekes & Lumley Reference Tennekes and Lumley1972; Townsend Reference Townsend1976). Moreover, accurate estimation of the turbulent production and dissipation rates is a challenge experimentally. Here, we estimate production using
$z<r\ll {\it\delta}$
), although its effect is probably not required at this Reynolds number. This is primarily due to the fact that the turbulent production and dissipation rates are nominally equal in the logarithmic region at sufficiently high Reynolds numbers (Tennekes & Lumley Reference Tennekes and Lumley1972; Townsend Reference Townsend1976). Moreover, accurate estimation of the turbulent production and dissipation rates is a challenge experimentally. Here, we estimate production using
![]() $\mathscr{P}\approx 1/{\it\kappa}z^{+}$
, while for the dissipation rate several estimates can be employed and are summarised in table 2 for the hot-wire dataset at
$\mathscr{P}\approx 1/{\it\kappa}z^{+}$
, while for the dissipation rate several estimates can be employed and are summarised in table 2 for the hot-wire dataset at
![]() $Re_{{\it\tau}}\approx 19\,000$
(Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009). All the estimates use the assumption of isotropy (see Pope (Reference Pope2000) for a detailed comparison); however, the third method (column 3) based on the third-order structure function has been reported to have less ambiguity (Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). The estimates of
$Re_{{\it\tau}}\approx 19\,000$
(Hutchins et al.
Reference Hutchins, Nickels, Marusic and Chong2009). All the estimates use the assumption of isotropy (see Pope (Reference Pope2000) for a detailed comparison); however, the third method (column 3) based on the third-order structure function has been reported to have less ambiguity (Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). The estimates of
![]() ${\it\epsilon}$
show an uncertainty of
${\it\epsilon}$
show an uncertainty of
![]() ${\approx}\!\pm 20\,\%$
between the methods used, comparable with prior observations by Kunkel & Marusic (Reference Kunkel and Marusic2006) and others. It is also worth highlighting that recent work particularly using numerical databases (where one can accurately compute
${\approx}\!\pm 20\,\%$
between the methods used, comparable with prior observations by Kunkel & Marusic (Reference Kunkel and Marusic2006) and others. It is also worth highlighting that recent work particularly using numerical databases (where one can accurately compute
![]() $\mathscr{P}$
and
$\mathscr{P}$
and
![]() ${\it\epsilon}$
) has aimed to answer the validity of the balance between
${\it\epsilon}$
) has aimed to answer the validity of the balance between
![]() $\mathscr{P}$
and
$\mathscr{P}$
and
![]() ${\it\epsilon}$
in the inertial region of wall turbulence (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015, and others). The results have largely shown support for the validity of an approximate balance, thus matching prior experimental observations.
${\it\epsilon}$
in the inertial region of wall turbulence (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014; Lee & Moser Reference Lee and Moser2015, and others). The results have largely shown support for the validity of an approximate balance, thus matching prior experimental observations.
Table 2. Dissipation rates
![]() ${\it\epsilon}$
(given in
${\it\epsilon}$
(given in
![]() $\text{m}^{2}~\text{s}^{-3}$
) computed from the hot-wire dataset of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) at
$\text{m}^{2}~\text{s}^{-3}$
) computed from the hot-wire dataset of Hutchins et al. (Reference Hutchins, Nickels, Marusic and Chong2009) at
![]() $Re_{{\it\tau}}\approx 19\,000$
, using three different methods.
$Re_{{\it\tau}}\approx 19\,000$
, using three different methods.

In figure 4 we consider data in the logarithmic region across the other datasets at varying Reynolds numbers. Results are presented on both log–log and log–linear scales to highlight the scaling described previously in § 2. For the inertial subrange shown in figure 4(a) evidence of a power-law scaling given by (2.8) is prevalent in all datasets with a scaling exponent close to
![]() $2/3$
. Similarly, a power-law scaling given by (2.4) is observed at the smallest scales within the dissipative range with a scaling exponent of 2. Further, a
$2/3$
. Similarly, a power-law scaling given by (2.4) is observed at the smallest scales within the dissipative range with a scaling exponent of 2. Further, a
![]() $\text{ln}(r/z)$
law in the form given by (2.9) is observed at scales larger than the inertial subrange in figure 4(b). All scaling regimes are indicated by the solid lines, together with their corresponding coefficients. The low Reynolds number dataset (▫ symbols) is included to demonstrate a clear trend with changing Reynolds number, and it emphasises the importance of higher Reynolds number data (
$\text{ln}(r/z)$
law in the form given by (2.9) is observed at scales larger than the inertial subrange in figure 4(b). All scaling regimes are indicated by the solid lines, together with their corresponding coefficients. The low Reynolds number dataset (▫ symbols) is included to demonstrate a clear trend with changing Reynolds number, and it emphasises the importance of higher Reynolds number data (
![]() $Re_{{\it\tau}}=O(10^{4}{-}10^{5})$
) to obtain a sufficiently large scale separation and thus observe all scaling behaviours simultaneously. In future efforts, it will also be valuable to consider whether the scaling behaviour reported extends to the transverse structure function, which has been examined previously by Kurien et al. (Reference Kurien, Lvov, Procaccia and Sreenivasan2000), Jacob et al. (Reference Jacob, Biferale, Iuso and Casciola2004) and others. As a final note, certain studies have reported power-law behaviour for structure functions (Benzi et al.
Reference Benzi, Amati, Casciola, Toschi and Piva1999; Toschi et al.
Reference Toschi, Amati, Succi, Benzi and Piva1999; Jacob et al.
Reference Jacob, Biferale, Iuso and Casciola2004, and others), albeit with particular focus on the smaller scales. Our analysis shows clear evidence of a power law in the range
$Re_{{\it\tau}}=O(10^{4}{-}10^{5})$
) to obtain a sufficiently large scale separation and thus observe all scaling behaviours simultaneously. In future efforts, it will also be valuable to consider whether the scaling behaviour reported extends to the transverse structure function, which has been examined previously by Kurien et al. (Reference Kurien, Lvov, Procaccia and Sreenivasan2000), Jacob et al. (Reference Jacob, Biferale, Iuso and Casciola2004) and others. As a final note, certain studies have reported power-law behaviour for structure functions (Benzi et al.
Reference Benzi, Amati, Casciola, Toschi and Piva1999; Toschi et al.
Reference Toschi, Amati, Succi, Benzi and Piva1999; Jacob et al.
Reference Jacob, Biferale, Iuso and Casciola2004, and others), albeit with particular focus on the smaller scales. Our analysis shows clear evidence of a power law in the range
![]() ${\it\eta}\ll r\ll z$
and a
${\it\eta}\ll r\ll z$
and a
![]() $\ln (r/z)$
law in the range
$\ln (r/z)$
law in the range
![]() $z<r\ll {\it\delta}$
. Some of these differences in interpretation may be attributed to the substantially higher Reynolds numbers examined in this study compared with prior work. This provides a large scale separation (large logarithmic region) enabling us to better discern any scaling behaviour. Moreover, a large proportion of studies that reported power-law behaviour alone employed decompositions primarily due to the lack of any scaling behaviour for the structure function in its classical form at the Reynolds numbers considered. Here, we present the structure function in its classical form, where the reported scaling behaviour is clearly observed.
$z<r\ll {\it\delta}$
. Some of these differences in interpretation may be attributed to the substantially higher Reynolds numbers examined in this study compared with prior work. This provides a large scale separation (large logarithmic region) enabling us to better discern any scaling behaviour. Moreover, a large proportion of studies that reported power-law behaviour alone employed decompositions primarily due to the lack of any scaling behaviour for the structure function in its classical form at the Reynolds numbers considered. Here, we present the structure function in its classical form, where the reported scaling behaviour is clearly observed.

Figure 4. Plots of
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
$\langle {\rm\Delta}u_{+}^{2}\rangle$
versus
![]() $r/z$
on (a) log–log and (b) linear–log scales. The symbols represent different datasets and are defined in table 1. Wall-normal locations: ▫,
$r/z$
on (a) log–log and (b) linear–log scales. The symbols represent different datasets and are defined in table 1. Wall-normal locations: ▫,
![]() $z^{+}\approx 200$
; ♢,
$z^{+}\approx 200$
; ♢,
![]() $z^{+}\approx 800$
; ▵,
$z^{+}\approx 800$
; ▵,
![]() $z^{+}\approx 1.6\times 10^{4}$
; ○, ●,
$z^{+}\approx 1.6\times 10^{4}$
; ○, ●,
![]() $z^{+}\approx 800$
. The solid lines correspond to fits (detailed further in § 6) in the ranges
$z^{+}\approx 800$
. The solid lines correspond to fits (detailed further in § 6) in the ranges
![]() ${\it\eta}\ll r\ll z$
and
${\it\eta}\ll r\ll z$
and
![]() $z<r\ll {\it\delta}$
. The heavy solid lines in (a) at the smallest
$z<r\ll {\it\delta}$
. The heavy solid lines in (a) at the smallest
![]() $r/z$
represent fits to each hot-wire dataset in the dissipative range.
$r/z$
represent fits to each hot-wire dataset in the dissipative range.
The good agreement between the PIV (denoted by ○, ● symbols) and hot-wire results in figure 4 highlights that the use of Taylor’s frozen turbulence hypothesis to convert the time-series information from the hot wires to spatial information is justified for the data presented here, at least up to
![]() $r<{\it\delta}$
. This concurs with previous findings where other statistical information is compared when Taylor’s approximation is invoked, such as in the study of Dennis & Nickels (Reference Dennis and Nickels2008). Other studies that have assessed the accuracy of invoking Taylor’s hypothesis include Del Alamo & Jiménez (Reference Del Alamo and Jiménez2009), Chung & McKeon (Reference Chung and McKeon2010) and Atkinson, Buchmann & Soria (Reference Atkinson, Buchmann and Soria2014).
$r<{\it\delta}$
. This concurs with previous findings where other statistical information is compared when Taylor’s approximation is invoked, such as in the study of Dennis & Nickels (Reference Dennis and Nickels2008). Other studies that have assessed the accuracy of invoking Taylor’s hypothesis include Del Alamo & Jiménez (Reference Del Alamo and Jiménez2009), Chung & McKeon (Reference Chung and McKeon2010) and Atkinson, Buchmann & Soria (Reference Atkinson, Buchmann and Soria2014).
4.2. Higher-order structure functions
Previously, we described the analogous postulate for higher-order structure functions in (2.12), extending prior work by Meneveau & Marusic (Reference Meneveau and Marusic2013) for higher-order moments of velocity fluctuations. This section considers empirical evidence for (2.12) based on the experimental data.
To begin, we apply the format used in figure 2 for the eighth-order structure function, which is shown in figure 5. It is immediately evident from figure 5 that the behaviour of the eighth-order structure function (after taking the
![]() $1/4$
root) is qualitatively comparable with its second-order counterpart. The region highlighted in green on the surface denotes the region where a
$1/4$
root) is qualitatively comparable with its second-order counterpart. The region highlighted in green on the surface denotes the region where a
![]() $\text{ln}(r/z)$
law seems to be prevalent, thus providing empirical support for (2.12). To further validate this observation, figure 6 presents results for the even higher-order moments at a single wall-normal location within the logarithmic region across all the experimental datasets considered, here shown up to
$\text{ln}(r/z)$
law seems to be prevalent, thus providing empirical support for (2.12). To further validate this observation, figure 6 presents results for the even higher-order moments at a single wall-normal location within the logarithmic region across all the experimental datasets considered, here shown up to
![]() $2p=10$
. To accentuate the analogous scaling behaviour observed in the second-order structure function (see figure 4), the solid lines from
$2p=10$
. To accentuate the analogous scaling behaviour observed in the second-order structure function (see figure 4), the solid lines from
![]() $2p=4{-}10$
in figure 6 represent power- and log-law fits to the HRNBLWT hot-wire dataset. The corresponding coefficients are also indicated in the figure. The universality of these coefficients for the datasets considered will be explored in § 6. The low
$2p=4{-}10$
in figure 6 represent power- and log-law fits to the HRNBLWT hot-wire dataset. The corresponding coefficients are also indicated in the figure. The universality of these coefficients for the datasets considered will be explored in § 6. The low
![]() $Re$
dataset at higher moments shows a deviation from the high
$Re$
dataset at higher moments shows a deviation from the high
![]() $Re$
datasets. This can be attributed to a much smaller logarithmic layer at low
$Re$
datasets. This can be attributed to a much smaller logarithmic layer at low
![]() $Re$
. Similar
$Re$
. Similar
![]() $Re$
dependence was also observed by Meneveau & Marusic (Reference Meneveau and Marusic2013) for higher-order moments of the streamwise velocity fluctuations below
$Re$
dependence was also observed by Meneveau & Marusic (Reference Meneveau and Marusic2013) for higher-order moments of the streamwise velocity fluctuations below
![]() $Re_{{\it\tau}}<7000$
. Our results from structure functions of higher orders are consistent with these findings; that is, beyond this threshold, the higher-order moments are independent of
$Re_{{\it\tau}}<7000$
. Our results from structure functions of higher orders are consistent with these findings; that is, beyond this threshold, the higher-order moments are independent of
![]() $Re$
. Therefore, we omit the low
$Re$
. Therefore, we omit the low
![]() $Re$
dataset in the subsequent analyses, particularly when computing the coefficients associated with the scaling fits described in § 5.
$Re$
dataset in the subsequent analyses, particularly when computing the coefficients associated with the scaling fits described in § 5.
Figure 7 shows the higher-order results for the data shown in figure 3(a) for various wall-normal positions throughout the logarithmic region. The results show good collapse of the higher moments up to
![]() $2p=10$
and provide further direct support for (2.12) across the entire extent of the logarithmic region.
$2p=10$
and provide further direct support for (2.12) across the entire extent of the logarithmic region.

Figure 7. Higher-order even structure functions for the same data as presented in figure 3 for various wall-normal positions throughout the logarithmic region for
![]() $Re_{{\it\tau}}=19\,000$
: (a,b)
$Re_{{\it\tau}}=19\,000$
: (a,b)
![]() $2p=6$
; (c,d)
$2p=6$
; (c,d)
![]() $2p=10$
. The symbols, solid lines and wall positions are defined in table 1 and figure 3 respectively.
$2p=10$
. The symbols, solid lines and wall positions are defined in table 1 and figure 3 respectively.
5. Statistical and attached-eddy interpretations in the
 $\ln (r/z)$
range
$\ln (r/z)$
range
In light of the supportive empirical results from the experimental data in § 4.2 for all even higher-order moments based on (2.12), we now aim to bridge the relations previously postulated for the higher-order structure functions with high-order moments of velocity fluctuations. We note that the analysis to follow applies to the inertial range of structure functions within the bounds
![]() $z<r\ll {\it\delta}$
. Two approaches are described in this work. First, we propose a generalisation of the work of Meneveau & Marusic (Reference Meneveau and Marusic2013) to higher-order structure functions. We subsequently complement the findings that arise from this generalisation with a physical model of a turbulent boundary layer based on the attached-eddy hypothesis.
$z<r\ll {\it\delta}$
. Two approaches are described in this work. First, we propose a generalisation of the work of Meneveau & Marusic (Reference Meneveau and Marusic2013) to higher-order structure functions. We subsequently complement the findings that arise from this generalisation with a physical model of a turbulent boundary layer based on the attached-eddy hypothesis.
5.1. Relations between high-order moments of velocity fluctuations and structure functions
Previously, § 2.4 summarised the results from Meneveau & Marusic (Reference Meneveau and Marusic2013) for the general behaviour of higher-order velocity fluctuations. Following their work, it is fruitful to develop the limit of structure functions at
![]() $r\gg {\it\delta}$
, by making use of the binomial theorem:
$r\gg {\it\delta}$
, by making use of the binomial theorem:
When
![]() $r\gg {\it\delta}$
, we expect
$r\gg {\it\delta}$
, we expect
![]() $u_{+}(x+r)$
and
$u_{+}(x+r)$
and
![]() $u_{+}(x)$
to become statistically independent, and hence
$u_{+}(x)$
to become statistically independent, and hence
![]() $\langle u_{+}(x+r)^{a}u_{+}(x)^{b}\rangle =\langle u_{+}(x)^{a}\rangle \langle u_{+}(x)^{b}\rangle$
. Therefore,
$\langle u_{+}(x+r)^{a}u_{+}(x)^{b}\rangle =\langle u_{+}(x)^{a}\rangle \langle u_{+}(x)^{b}\rangle$
. Therefore,
If we assume that the odd moments all vanish, then this is equivalent to only adding the positive even terms:
For
![]() $p=1$
, this becomes the familiar
$p=1$
, this becomes the familiar
![]() $\langle [u_{+}(\boldsymbol{x}+\boldsymbol{i}r)-u_{+}(\boldsymbol{x})]^{2}\rangle \rightarrow 2\langle u_{+}^{2}\rangle$
. For
$\langle [u_{+}(\boldsymbol{x}+\boldsymbol{i}r)-u_{+}(\boldsymbol{x})]^{2}\rangle \rightarrow 2\langle u_{+}^{2}\rangle$
. For
![]() $p=2$
, the relationship is
$p=2$
, the relationship is
![]() $\langle [u_{+}(\boldsymbol{x}+\boldsymbol{i}r)-u_{+}(\boldsymbol{x})]^{4}\rangle \rightarrow 2\langle u_{+}^{4}\rangle +6\langle u_{+}^{2}\rangle ^{2}$
. Using this in the context of the generalised logarithmic laws, for even moments only, we expect
$\langle [u_{+}(\boldsymbol{x}+\boldsymbol{i}r)-u_{+}(\boldsymbol{x})]^{4}\rangle \rightarrow 2\langle u_{+}^{4}\rangle +6\langle u_{+}^{2}\rangle ^{2}$
. Using this in the context of the generalised logarithmic laws, for even moments only, we expect
To simplify, it is useful to absorb the coefficient
![]() $B_{k}$
inside the logarithm, by setting
$B_{k}$
inside the logarithm, by setting
![]() $c_{k}=\exp (B_{k}/A_{k})$
, then we obtain
$c_{k}=\exp (B_{k}/A_{k})$
, then we obtain
Next, we make the reasonable assumption that
![]() $B_{p}$
(as well as
$B_{p}$
(as well as
![]() $c_{p}$
) does not depend much on the moment order (e.g. that the intercepts of all moment log-laws occur roughly at the same outer length scale
$c_{p}$
) does not depend much on the moment order (e.g. that the intercepts of all moment log-laws occur roughly at the same outer length scale
![]() $c_{p}{\it\delta}\approx c{\it\delta}$
, and based on the measurements of
$c_{p}{\it\delta}\approx c{\it\delta}$
, and based on the measurements of
![]() $B_{1}\approx 1.7$
and
$B_{1}\approx 1.7$
and
![]() $A_{1}\approx 1.25$
we may estimate
$A_{1}\approx 1.25$
we may estimate
![]() $c\approx 4$
); this seems to be supported by the data. We can then write
$c\approx 4$
); this seems to be supported by the data. We can then write
and we obtain a logarithmic dependence of the structure function asymptote at
![]() $r\gg {\it\delta}$
:
$r\gg {\it\delta}$
:
where
Given numeric values for
![]() $A_{p}$
for
$A_{p}$
for
![]() $p=1{-}5$
measured in Meneveau & Marusic (Reference Meneveau and Marusic2013), numerical values for
$p=1{-}5$
measured in Meneveau & Marusic (Reference Meneveau and Marusic2013), numerical values for
![]() $G_{p}$
can be obtained. For instance, for second-order structure functions,
$G_{p}$
can be obtained. For instance, for second-order structure functions,
![]() $p=1$
, we obtain
$p=1$
, we obtain
and for fourth-order ones,
![]() $p=2$
, we have
$p=2$
, we have
A comparison of these coefficients against experimental results will be presented in § 6.
5.2. The attached-eddy hypothesis and higher-order moments
In this section, we compare the observed statistical behaviour of the structure functions with that predicted by modelling the flow from elementary physical principles. To this end, we derive various properties of the structure functions in the logarithmic region from the attached-eddy hypothesis. This hypothesis states that the logarithmic region is dominated and characterised by the presence of a hierarchy of self-similar coherent structures, or ‘eddies’, whose sizes scale with their distances from the wall. It is in this loose sense that the eddies are said to be ‘attached’ to the wall. This will enable us to explore the validity of the current manifestation of the attached-eddy hypothesis as a potential predictive model for structure functions in the logarithmic region of turbulent wall flows.
The attached-eddy hypothesis, as it is applied here, assumes that the locations of the eddies on the wall are perfectly random and independent of each other. This has allowed the statistical properties of the flow to be derived via Campbell’s theorem. This model has been used by Woodcock & Marusic (Reference Woodcock and Marusic2015) to derive the moments of the velocity in the logarithmic region. The model treats the flow as a superposition of the velocity fields corresponding to each of a multitude of geometrically equivalent eddies. The locations of the eddies are perfectly random and are unaffected by the presence of nearby eddies. (This means that the eddies are not prevented from overlapping, and two or more eddies may occupy the same region of space.) The eddies are identical once scaled by their heights, and their shapes are unaffected by the presence of nearby eddies. The reasoning behind the attached-eddy hypothesis, as well as the derivation extended here, has been further elaborated upon by Woodcock & Marusic (Reference Woodcock and Marusic2015).
The height of any particular eddy,
![]() $h$
, is assumed to be between
$h$
, is assumed to be between
![]() $h_{min}$
and
$h_{min}$
and
![]() $h_{max}$
. We can therefore equate
$h_{max}$
. We can therefore equate
![]() $h_{max}$
with
$h_{max}$
with
![]() ${\it\delta}$
, the thickness of the boundary layer. In order to simplify the subsequent equations, we will introduce some new symbols. Since each eddy is characterised by its height, it is sensible to scale all lengths by
${\it\delta}$
, the thickness of the boundary layer. In order to simplify the subsequent equations, we will introduce some new symbols. Since each eddy is characterised by its height, it is sensible to scale all lengths by
![]() $h$
. Hence, we scale the location vector,
$h$
. Hence, we scale the location vector,
![]() $\boldsymbol{x}$
, and the displacement via
$\boldsymbol{x}$
, and the displacement via
When deriving the velocity moments, Campbell’s theorem reduces the derivation to an integral over the velocity field corresponding to a single eddy. Hence, if the vector
![]() $\boldsymbol{Q}(\boldsymbol{X})$
represents the velocity field corresponding to a single eddy, then we can express all moments of the velocity in terms of
$\boldsymbol{Q}(\boldsymbol{X})$
represents the velocity field corresponding to a single eddy, then we can express all moments of the velocity in terms of
![]() $\boldsymbol{Q}(\boldsymbol{X})$
.
$\boldsymbol{Q}(\boldsymbol{X})$
.
Since each eddy is spatially bounded, the velocity field corresponding to each eddy will inevitably be negligible at a sufficient distance from the location of the eddy, and this distance is proportional to the height of the eddy. Using this, Woodcock & Marusic (Reference Woodcock and Marusic2015) showed that the log-law for the flow profile follows from Campbell’s theorem.
When applied to the derivation of the structure function, Campbell’s theorem reduces the derivation to an integral over a pair of eddies identical in magnitude but of opposite sign, a distance of
![]() $r$
apart. We therefore introduce a new function,
$r$
apart. We therefore introduce a new function,
![]() ${\rm\Delta}I_{k}\left(\boldsymbol{X},R\right)$
, which we call the eddy difference contribution. It relates the flow field corresponding to a single eddy via
${\rm\Delta}I_{k}\left(\boldsymbol{X},R\right)$
, which we call the eddy difference contribution. It relates the flow field corresponding to a single eddy via
This we can relate to
![]() $\langle {\rm\Delta}u_{+}^{n}\rangle$
through a mathematical intermediary, which we call a cumulant. These cumulants, denoted by
$\langle {\rm\Delta}u_{+}^{n}\rangle$
through a mathematical intermediary, which we call a cumulant. These cumulants, denoted by
![]() ${\it\Lambda}_{k}(\boldsymbol{x},r)$
, are defined by
${\it\Lambda}_{k}(\boldsymbol{x},r)$
, are defined by
where
![]() ${\it\beta}$
denotes the density of the eddies on the wall and
${\it\beta}$
denotes the density of the eddies on the wall and
![]() $P(h)$
is the probability density function for the height of an eddy. Woodcock & Marusic (Reference Woodcock and Marusic2015) have shown that this is given by
$P(h)$
is the probability density function for the height of an eddy. Woodcock & Marusic (Reference Woodcock and Marusic2015) have shown that this is given by
The structure functions can be shown to relate to the cumulants via
 $$\begin{eqnarray}\displaystyle \langle {\rm\Delta}u_{+}^{10}\rangle & = & \displaystyle {\it\Lambda}_{10}+45{\it\Lambda}_{2}{\it\Lambda}_{8}+120{\it\Lambda}_{3}{\it\Lambda}_{7}+210{\it\Lambda}_{4}{\it\Lambda}_{6}+630{\it\Lambda}_{2}^{2}{\it\Lambda}_{6}+126{\it\Lambda}_{5}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,2520{\it\Lambda}_{2}{\it\Lambda}_{3}{\it\Lambda}_{5}+1575{\it\Lambda}_{2}{\it\Lambda}_{4}^{2}+2100{\it\Lambda}_{3}^{2}{\it\Lambda}_{4}+3150{\it\Lambda}_{2}^{3}{\it\Lambda}_{4}\nonumber\\ \displaystyle & & \displaystyle +\,6300{\it\Lambda}_{2}^{2}{\it\Lambda}_{3}^{2}+945{\it\Lambda}_{2}^{5}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle {\rm\Delta}u_{+}^{10}\rangle & = & \displaystyle {\it\Lambda}_{10}+45{\it\Lambda}_{2}{\it\Lambda}_{8}+120{\it\Lambda}_{3}{\it\Lambda}_{7}+210{\it\Lambda}_{4}{\it\Lambda}_{6}+630{\it\Lambda}_{2}^{2}{\it\Lambda}_{6}+126{\it\Lambda}_{5}^{2}\nonumber\\ \displaystyle & & \displaystyle +\,2520{\it\Lambda}_{2}{\it\Lambda}_{3}{\it\Lambda}_{5}+1575{\it\Lambda}_{2}{\it\Lambda}_{4}^{2}+2100{\it\Lambda}_{3}^{2}{\it\Lambda}_{4}+3150{\it\Lambda}_{2}^{3}{\it\Lambda}_{4}\nonumber\\ \displaystyle & & \displaystyle +\,6300{\it\Lambda}_{2}^{2}{\it\Lambda}_{3}^{2}+945{\it\Lambda}_{2}^{5}.\end{eqnarray}$$
The derivation of the structure functions is analogous to that presented by Woodcock & Marusic (Reference Woodcock and Marusic2015) for the moments of the velocity. The details of this derivation can be found in appendix A. These derivations apply where
(It should be noted that we have specifically made use of the fact that we equate
![]() $h_{max}$
with the height of the boundary layer,
$h_{max}$
with the height of the boundary layer,
![]() ${\it\delta}$
in the above equation.) In this limit, the even-ordered cumulants will obey
${\it\delta}$
in the above equation.) In this limit, the even-ordered cumulants will obey
where
![]() $\mathscr{A}_{k}$
and
$\mathscr{A}_{k}$
and
![]() $\mathscr{B}_{k}$
are constants. The constant
$\mathscr{B}_{k}$
are constants. The constant
![]() $\mathscr{A}_{k}$
is given by
$\mathscr{A}_{k}$
is given by
(We could give a similar expression for
![]() $\mathscr{B}_{k}$
. However, since the attached-eddy model contains different boundary conditions from real turbulent flows, any
$\mathscr{B}_{k}$
. However, since the attached-eddy model contains different boundary conditions from real turbulent flows, any
![]() $\mathscr{B}_{k}$
derived in this way would not be physically significant.)
$\mathscr{B}_{k}$
derived in this way would not be physically significant.)
We can express the range of eddy sizes present as a Reynolds number. This Reynolds number can be conventionally defined by
which is based on the assumption that
![]() $h_{max}={\it\delta}$
and
$h_{max}={\it\delta}$
and
![]() $h_{min}=100$
following Kline et al. (Reference Kline, Reynolds, Schraub and Runstadler1967). By an analogous derivation to that given by Woodcock & Marusic (Reference Woodcock and Marusic2015), it can be shown that (5.18) can be re-expressed as
$h_{min}=100$
following Kline et al. (Reference Kline, Reynolds, Schraub and Runstadler1967). By an analogous derivation to that given by Woodcock & Marusic (Reference Woodcock and Marusic2015), it can be shown that (5.18) can be re-expressed as
where
![]() $k_{x}$
is a constant defined such that the expected distance to the next closest eddy in the positive
$k_{x}$
is a constant defined such that the expected distance to the next closest eddy in the positive
![]() $x$
direction will always be
$x$
direction will always be
![]() $k_{x}h$
if the height of the next closest eddy were known to be
$k_{x}h$
if the height of the next closest eddy were known to be
![]() $h$
. (More specifically,
$h$
. (More specifically,
![]() $k_{x}h$
represents the distance in a strip of height
$k_{x}h$
represents the distance in a strip of height
![]() $h^{\prime }$
to the nearest eddy of height between
$h^{\prime }$
to the nearest eddy of height between
![]() $h$
and
$h$
and
![]() $h+\text{d}h$
divided by
$h+\text{d}h$
divided by
![]() $h^{\prime }$
and
$h^{\prime }$
and
![]() $\text{d}h$
.) The constant
$\text{d}h$
.) The constant
![]() $k_{y}$
is its spanwise equivalent.
$k_{y}$
is its spanwise equivalent.
In the large-
![]() $Re_{{\it\tau}}$
limit, this asymptotes to
$Re_{{\it\tau}}$
limit, this asymptotes to
As we can easily see in (5.15),
![]() ${\it\Lambda}_{2}$
is equivalent to the second-order structure function. We can therefore return (2.9), the logarithmic law for
${\it\Lambda}_{2}$
is equivalent to the second-order structure function. We can therefore return (2.9), the logarithmic law for
![]() $\langle {\rm\Delta}u_{+}^{2}\rangle$
, by stating that
$\langle {\rm\Delta}u_{+}^{2}\rangle$
, by stating that
![]() $\mathscr{A}_{2}\equiv D_{1}$
and
$\mathscr{A}_{2}\equiv D_{1}$
and
![]() $\mathscr{B}_{2}\equiv E_{1}$
.
$\mathscr{B}_{2}\equiv E_{1}$
.
It can also be observed that by considering (5.13) the higher even-ordered structure functions will be dominated by their final term (which is the component containing the highest power of
![]() ${\it\Lambda}_{2}$
) in the limit as
${\it\Lambda}_{2}$
) in the limit as
![]() ${\it\beta}\rightarrow \infty$
. Given the relationship between
${\it\beta}\rightarrow \infty$
. Given the relationship between
![]() ${\it\Lambda}_{2}$
and the second-order structure function, we can easily see that (5.17) returns a logarithmic law for the second-order structure function given in (2.9). Furthermore, for large
${\it\Lambda}_{2}$
and the second-order structure function, we can easily see that (5.17) returns a logarithmic law for the second-order structure function given in (2.9). Furthermore, for large
![]() ${\it\beta}$
(
${\it\beta}$
(
![]() ${\it\beta}\rightarrow \infty$
), it can be seen that the even-numbered higher-ordered structure functions will obey
${\it\beta}\rightarrow \infty$
), it can be seen that the even-numbered higher-ordered structure functions will obey
where
![]() $D_{p}$
and
$D_{p}$
and
![]() $E_{p}$
are constants which are equivalent to
$E_{p}$
are constants which are equivalent to
![]() $\mathscr{A}_{2p}$
and
$\mathscr{A}_{2p}$
and
![]() $\mathscr{B}_{2p}$
respectively. Importantly, this concurs with experimental results, as will be discussed in more detail in § 6. We also note that carrying out the above derivations for the other velocity components shows a similar logarithmic relation for the spanwise velocity, but not for the wall-normal velocity.
$\mathscr{B}_{2p}$
respectively. Importantly, this concurs with experimental results, as will be discussed in more detail in § 6. We also note that carrying out the above derivations for the other velocity components shows a similar logarithmic relation for the spanwise velocity, but not for the wall-normal velocity.
The odd-ordered cumulants have also been derived in appendix A. Their behaviour is given in (A 25). They are likely to be of much lower magnitude than their even-ordered counterparts wherever (5.16) applies, so their contributions to the even-ordered structure functions should be negligible. Their contributions to the odd-ordered structure functions are more significant, but since these are of less interest, we do not reproduce them here.
Therefore, we can see that the attached-eddy hypothesis produces predictions for the structure functions in the logarithmic region that are in qualitative agreement with experimental evidence. In order to extend this to a quantitative prediction for the structure functions, it would be necessary to produce a specific function for
![]() $\boldsymbol{Q}(\boldsymbol{x})$
, the velocity field corresponding to a single eddy. This is, however, beyond the scope of this present work.
$\boldsymbol{Q}(\boldsymbol{x})$
, the velocity field corresponding to a single eddy. This is, however, beyond the scope of this present work.

Figure 8. Plots of
![]() $\langle {\rm\Delta}u_{+}^{2p}\rangle ^{1/p}(r/z)^{{\it\xi}_{2p}/p}$
versus
$\langle {\rm\Delta}u_{+}^{2p}\rangle ^{1/p}(r/z)^{{\it\xi}_{2p}/p}$
versus
![]() $r/z$
on a linear–log scale at
$r/z$
on a linear–log scale at
![]() $p=1{-}5$
. The symbols represent different datasets: ●, HRNBLWT – high-mag PIV; ♢, HRNBLWT – hot-wire; ▵, SLTEST – hot-wire. Wall-normal locations: ♢,
$p=1{-}5$
. The symbols represent different datasets: ●, HRNBLWT – high-mag PIV; ♢, HRNBLWT – hot-wire; ▵, SLTEST – hot-wire. Wall-normal locations: ♢,
![]() $z^{+}\approx 800$
; ▵,
$z^{+}\approx 800$
; ▵,
![]() $z^{+}\approx 1.6\times 10^{4}$
; ●,
$z^{+}\approx 1.6\times 10^{4}$
; ●,
![]() $z^{+}\approx 800$
. The horizontal dashed line indicates the computed multiplicative constant
$z^{+}\approx 800$
. The horizontal dashed line indicates the computed multiplicative constant
![]() $M_{p}$
in the inertial subrange
$M_{p}$
in the inertial subrange
![]() ${\it\eta}\ll r\ll z$
based on the SLTEST dataset (▵ symbols). The vertical dashed line corresponds to the transitional length scale
${\it\eta}\ll r\ll z$
based on the SLTEST dataset (▵ symbols). The vertical dashed line corresponds to the transitional length scale
![]() $L_{s}$
.
$L_{s}$
.
6. Evaluation of the universal coefficients
This section revisits the experimental results for the scaling of the streamwise structure function with particular focus on the inertial subrange (
![]() ${\it\eta}\ll r\ll z$
) and the
${\it\eta}\ll r\ll z$
) and the
![]() $\ln (r/z)$
range (
$\ln (r/z)$
range (
![]() $z<r\ll {\it\delta}$
). For the inertial subrange the two coefficients
$z<r\ll {\it\delta}$
). For the inertial subrange the two coefficients
![]() ${\it\xi}_{2p}$
and
${\it\xi}_{2p}$
and
![]() $M_{p}$
are investigated following the power-law scaling given by (2.8). To do so we compute
$M_{p}$
are investigated following the power-law scaling given by (2.8). To do so we compute
![]() $\langle {\rm\Delta}u_{+}^{2p}\rangle ^{1/p}(r/z)^{{\it\xi}_{2p}/p}$
and present the results on log–linear plots, as shown in figure 8. From (2.8) a plateau should appear in the inertial subrange. The results in figure 8 do indeed show a plateau, but only convincingly for the very high Reynolds number atmospheric boundary layer data. The wind tunnel data at lower Reynolds number are seen to have a limited inertial subrange as is expected.
$\langle {\rm\Delta}u_{+}^{2p}\rangle ^{1/p}(r/z)^{{\it\xi}_{2p}/p}$
and present the results on log–linear plots, as shown in figure 8. From (2.8) a plateau should appear in the inertial subrange. The results in figure 8 do indeed show a plateau, but only convincingly for the very high Reynolds number atmospheric boundary layer data. The wind tunnel data at lower Reynolds number are seen to have a limited inertial subrange as is expected.
The results in figure 8 show that the power-law scaling extends to higher-order moments, at least up to
![]() $2p=10$
. The computed coefficients for
$2p=10$
. The computed coefficients for
![]() $M_{p}$
from the three datasets are shown in figure 9(a) and are listed in table 3. The scaling exponent
$M_{p}$
from the three datasets are shown in figure 9(a) and are listed in table 3. The scaling exponent
![]() ${\it\xi}_{2p}/p$
has been widely investigated in prior work (She & Leveque Reference She and Leveque1994; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997, to name a few). Conventionally, the scaling exponent is presented as
${\it\xi}_{2p}/p$
has been widely investigated in prior work (She & Leveque Reference She and Leveque1994; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997, to name a few). Conventionally, the scaling exponent is presented as
![]() ${\it\xi}_{2p}$
, and is shown in figure 9(b); for completeness figure 9(c) shows the scaling exponent
${\it\xi}_{2p}$
, and is shown in figure 9(b); for completeness figure 9(c) shows the scaling exponent
![]() ${\it\xi}_{2p}/p$
. The results show a strong deviation from the Kolmogorov estimate (K41), similar to that observed in several prior numerical and experimental studies, as summarised, for example, by She & Leveque (Reference She and Leveque1994). Nevertheless, the three datasets considered here show good collapse for
${\it\xi}_{2p}/p$
. The results show a strong deviation from the Kolmogorov estimate (K41), similar to that observed in several prior numerical and experimental studies, as summarised, for example, by She & Leveque (Reference She and Leveque1994). Nevertheless, the three datasets considered here show good collapse for
![]() ${\it\xi}_{2p}$
and are also in close proximity to prior results from the She–Leveque model (She & Leveque Reference She and Leveque1994). Overall the results in figures 8 and 9 support the hypothesis that the constants
${\it\xi}_{2p}$
and are also in close proximity to prior results from the She–Leveque model (She & Leveque Reference She and Leveque1994). Overall the results in figures 8 and 9 support the hypothesis that the constants
![]() ${\it\xi}_{2p}$
and
${\it\xi}_{2p}$
and
![]() $M_{p}$
in (2.8) are universal at high Reynolds numbers. This is based on results from three independent datasets, involving different experimental techniques, facilities and flow conditions (noting that the atmospheric boundary layer is a rough boundary layer).
$M_{p}$
in (2.8) are universal at high Reynolds numbers. This is based on results from three independent datasets, involving different experimental techniques, facilities and flow conditions (noting that the atmospheric boundary layer is a rough boundary layer).

Figure 9. (a) Multiplicative coefficient (
![]() $M_{p}$
) and (b) scaling exponent
$M_{p}$
) and (b) scaling exponent
![]() ${\it\xi}_{2p}/p$
of the base
${\it\xi}_{2p}/p$
of the base
![]() $r/z$
for
$r/z$
for
![]() $p=1{-}5$
in the inertial sublayer range (
$p=1{-}5$
in the inertial sublayer range (
![]() $(z^{+})^{-3/4}\ll r/z\ll 1$
). (c) Results in (a) reproduced but now scaled with
$(z^{+})^{-3/4}\ll r/z\ll 1$
). (c) Results in (a) reproduced but now scaled with
![]() $p$
. The symbols are defined in table 1. The dashed line in (b) and (c) represents the K41 law, and the solid and dotted lines correspond to numeric values provided in She & Leveque (Reference She and Leveque1994) (see (2.6)) and Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1987) (see (2.7)) respectively.
$p$
. The symbols are defined in table 1. The dashed line in (b) and (c) represents the K41 law, and the solid and dotted lines correspond to numeric values provided in She & Leveque (Reference She and Leveque1994) (see (2.6)) and Meneveau & Sreenivasan (Reference Meneveau and Sreenivasan1987) (see (2.7)) respectively.
Table 3. Comparison of the coefficients
![]() ${\it\xi}_{2p}$
and
${\it\xi}_{2p}$
and
![]() $M_{p}$
in the region
$M_{p}$
in the region
![]() $z<r<{\it\delta}$
from different datasets. For the HRNBLWT – hot-wire datasets results are presented only at
$z<r<{\it\delta}$
from different datasets. For the HRNBLWT – hot-wire datasets results are presented only at
![]() $Re_{{\it\tau}}\approx 19\,000$
.
$Re_{{\it\tau}}\approx 19\,000$
.


Figure 10. (a) The multiplicative coefficient (
![]() $D_{p}$
) of
$D_{p}$
) of
![]() $r/z$
at
$r/z$
at
![]() $p=1{-}5$
and (b) the additive coefficient (
$p=1{-}5$
and (b) the additive coefficient (
![]() $E_{p}$
) in the scaling range
$E_{p}$
) in the scaling range
![]() $z<r<{\it\delta}$
. The symbols are defined in table 1. The dashed line in (a) represents the expected behaviour for Gaussian statistics, where
$z<r<{\it\delta}$
. The symbols are defined in table 1. The dashed line in (a) represents the expected behaviour for Gaussian statistics, where
![]() $D_{p}=G_{p}$
as defined in (5.8), and the solid black line corresponds to numeric values provided in Meneveau & Marusic (Reference Meneveau and Marusic2013).
$D_{p}=G_{p}$
as defined in (5.8), and the solid black line corresponds to numeric values provided in Meneveau & Marusic (Reference Meneveau and Marusic2013).
Table 4. Comparison of the coefficients
![]() $D_{p}$
and
$D_{p}$
and
![]() $E_{p}$
in the region
$E_{p}$
in the region
![]() $z<r<{\it\delta}$
from different datasets. Here,
$z<r<{\it\delta}$
from different datasets. Here,
![]() $G_{p}$
is computed using numeric values provided in Meneveau & Marusic (Reference Meneveau and Marusic2013) and the estimate
$G_{p}$
is computed using numeric values provided in Meneveau & Marusic (Reference Meneveau and Marusic2013) and the estimate
![]() $D_{p}\approx G_{p}$
(where at
$D_{p}\approx G_{p}$
(where at
![]() $r\approx {\it\delta}$
we have
$r\approx {\it\delta}$
we have
![]() $\langle {\rm\Delta}u_{+}^{2p}\rangle$
from (5.3)). For the HRNBLWT – hot-wire datasets results are presented only at
$\langle {\rm\Delta}u_{+}^{2p}\rangle$
from (5.3)). For the HRNBLWT – hot-wire datasets results are presented only at
![]() $Re_{{\it\tau}}\approx 19\,000$
.
$Re_{{\it\tau}}\approx 19\,000$
.

For the inertial range within the bounds
![]() $z<r\ll {\it\delta}$
we expect to observe a
$z<r\ll {\it\delta}$
we expect to observe a
![]() $\ln (r/z)$
law in the form given in (5.22) for the higher-order structure functions. Figures 10(a) and 10(b) show comparisons of
$\ln (r/z)$
law in the form given in (5.22) for the higher-order structure functions. Figures 10(a) and 10(b) show comparisons of
![]() $D_{p}$
and
$D_{p}$
and
![]() $E_{p}$
respectively. Also included are the estimates computed using (5.8) with numerical values obtained from Meneveau & Marusic (Reference Meneveau and Marusic2013) for
$E_{p}$
respectively. Also included are the estimates computed using (5.8) with numerical values obtained from Meneveau & Marusic (Reference Meneveau and Marusic2013) for
![]() $A_{p}$
. Good agreement is observed between all high Reynolds number datasets considered both visually and quantitatively, as summarised in table 4. We note that the observed variations in the computed coefficients from the higher
$A_{p}$
. Good agreement is observed between all high Reynolds number datasets considered both visually and quantitatively, as summarised in table 4. We note that the observed variations in the computed coefficients from the higher
![]() $Re$
datasets are well within the experimental uncertainty of the datasets used. A larger discrepancy is observed between the experimental data and the estimates obtained from (5.8), which can be attributed to the assumptions described in § 5.1.
$Re$
datasets are well within the experimental uncertainty of the datasets used. A larger discrepancy is observed between the experimental data and the estimates obtained from (5.8), which can be attributed to the assumptions described in § 5.1.
In figure 8 we also consider the demarcation of the
![]() $\ln (r/z)$
range and the inertial subrange using the transitional length scale (
$\ln (r/z)$
range and the inertial subrange using the transitional length scale (
![]() $L_{s}$
) in structure functions, which is defined as
$L_{s}$
) in structure functions, which is defined as
following Toschi et al. (Reference Toschi, Amati, Succi, Benzi and Piva1999). Since our analysis is confined to the logarithmic region of wall-bounded turbulence, we can use (2.3) to simplify (6.1) to
Similar to prior observations by Saikrishnan et al. (Reference Saikrishnan, De Angelis, Longmire, Marusic, Casciola and Piva2012), albeit at a significantly lower Reynolds number, figure 8 shows that the computed
![]() $L_{s}$
following (6.2) clearly demarcates two distinct scaling regions. At scales below
$L_{s}$
following (6.2) clearly demarcates two distinct scaling regions. At scales below
![]() $L_{s}$
a power-law scaling regime is observed, whereas at scales larger than
$L_{s}$
a power-law scaling regime is observed, whereas at scales larger than
![]() $L_{s}$
a less rapidly increasing trend is observed (namely proportional to
$L_{s}$
a less rapidly increasing trend is observed (namely proportional to
![]() $\ln (r/z)$
, as seen in figures 6 and 7).
$\ln (r/z)$
, as seen in figures 6 and 7).
6.1. Modelling of coefficients in the
 $\ln (r/z)$
range
$\ln (r/z)$
range
So far we have examined the inertial subrange and
![]() $\ln (r/z)$
range of the streamwise structure function independently. However, the results shown in figures 4 and 6 suggest that the scaling fits employed in each region intersect at approximately
$\ln (r/z)$
range of the streamwise structure function independently. However, the results shown in figures 4 and 6 suggest that the scaling fits employed in each region intersect at approximately
![]() $r/z\approx 1$
. This suggests the possibility of using this information to reduce the number of unknown constants. (Such matching approaches have been attempted previously, including in the more recent study by Davidson & Krogstad (Reference Davidson and Krogstad2009).) Therefore, using this purely empirical observation we equate the two fits and model/estimate the coefficients for the
$r/z\approx 1$
. This suggests the possibility of using this information to reduce the number of unknown constants. (Such matching approaches have been attempted previously, including in the more recent study by Davidson & Krogstad (Reference Davidson and Krogstad2009).) Therefore, using this purely empirical observation we equate the two fits and model/estimate the coefficients for the
![]() $\ln (r/z)$
range based on the scaling fits in the inertial subrange alone. To perform this, the two scaling fits given by (2.8) and (5.22) are equated to obtain
$\ln (r/z)$
range based on the scaling fits in the inertial subrange alone. To perform this, the two scaling fits given by (2.8) and (5.22) are equated to obtain
where
![]() $E_{p}^{\prime }$
and
$E_{p}^{\prime }$
and
![]() $D_{p}^{\prime }$
are modelled equivalents of
$D_{p}^{\prime }$
are modelled equivalents of
![]() $E_{p}$
and
$E_{p}$
and
![]() $D_{p}$
, and
$D_{p}$
, and
![]() $\mathscr{X}$
corresponds to the magnitude of
$\mathscr{X}$
corresponds to the magnitude of
![]() $r/z$
at the estimated point of intersection between the two scaling fits. By further matching gradients at
$r/z$
at the estimated point of intersection between the two scaling fits. By further matching gradients at
![]() $\mathscr{X}$
we obtain
$\mathscr{X}$
we obtain
which can be rearranged to give
Substituting (6.5) into (6.3) we can now estimate
![]() $E_{p}^{\prime }$
using
$E_{p}^{\prime }$
using
Visual inspection of the results presented for
![]() $\langle {\rm\Delta}u_{+}^{2p}\rangle ^{1/p}$
in figures 4 and 6 shows that
$\langle {\rm\Delta}u_{+}^{2p}\rangle ^{1/p}$
in figures 4 and 6 shows that
![]() $\mathscr{X}\approx 1$
; however, upon closer inspection a linear decrease in
$\mathscr{X}\approx 1$
; however, upon closer inspection a linear decrease in
![]() $\mathscr{X}$
is observed across all datasets, as shown in figure 11, with increasing
$\mathscr{X}$
is observed across all datasets, as shown in figure 11, with increasing
![]() $p$
. Therefore, following estimates of
$p$
. Therefore, following estimates of
![]() $\mathscr{X}$
from the experimental datasets, results for
$\mathscr{X}$
from the experimental datasets, results for
![]() $E_{p}^{\prime }$
and
$E_{p}^{\prime }$
and
![]() $D_{p}^{\prime }$
are summarised in table 5 and are compared with prior experimental results in figure 12. The results show that the magnitude and trend of the modelled coefficients closely match those computed directly from the experimental datasets.
$D_{p}^{\prime }$
are summarised in table 5 and are compared with prior experimental results in figure 12. The results show that the magnitude and trend of the modelled coefficients closely match those computed directly from the experimental datasets.

Figure 11. Variation of
![]() $\mathscr{X}$
computed from the SLTEST dataset of Kunkel & Marusic (Reference Kunkel and Marusic2006) at
$\mathscr{X}$
computed from the SLTEST dataset of Kunkel & Marusic (Reference Kunkel and Marusic2006) at
![]() $Re_{{\it\tau}}=3.1\times 10^{6}$
and
$Re_{{\it\tau}}=3.1\times 10^{6}$
and
![]() $z^{+}\approx 1.6\times 10^{4}$
. The solid line represents a linear fit which is used to obtain the results shown in figure 12.
$z^{+}\approx 1.6\times 10^{4}$
. The solid line represents a linear fit which is used to obtain the results shown in figure 12.

Figure 12. The same as figure 10, but with the inclusion of the modelled coefficients (▿ symbols) for the SLTEST dataset of Kunkel & Marusic (Reference Kunkel and Marusic2006), as summarised in table 5.
Table 5. Comparison of the coefficients
![]() $D_{p}$
and
$D_{p}$
and
![]() $E_{p}$
in the region
$E_{p}$
in the region
![]() $z<r<{\it\delta}$
from different datasets. For the HRNBLWT – hot-wire datasets results are presented only at
$z<r<{\it\delta}$
from different datasets. For the HRNBLWT – hot-wire datasets results are presented only at
![]() $Re_{{\it\tau}}\approx 19\,000$
.
$Re_{{\it\tau}}\approx 19\,000$
.

7. Summary and conclusions
Through the use of a uniquely large range of experimental datasets that span several decades of Reynolds numbers, this study investigates the scaling of higher-order streamwise structure functions. We present a description of formulations that characterise the scaling laws for the streamwise structure functions with particular focus on the logarithmic region in wall-normal space, which is characterised by a range of locations away from the wall, and within the Kolmogorov inertial subrange and
![]() $\ln (r/z)$
range in streamwise separation space.
$\ln (r/z)$
range in streamwise separation space.
The employment of datasets with Reynolds numbers extending to
![]() $Re_{{\it\tau}}=O(10^{6})$
enables us to observe both scaling laws simultaneously unlike most prior work. Furthermore, our analysis shows comparable results for a wide range of experimental datasets extending from laboratory experiments to the atmospheric boundary layer, thus showing a certain degree of universality for the computed coefficients of the scaling laws.
$Re_{{\it\tau}}=O(10^{6})$
enables us to observe both scaling laws simultaneously unlike most prior work. Furthermore, our analysis shows comparable results for a wide range of experimental datasets extending from laboratory experiments to the atmospheric boundary layer, thus showing a certain degree of universality for the computed coefficients of the scaling laws.
Following prior mathematical descriptions by Davidson and coworkers for the
![]() $\ln (r/z)$
range of the second-order structure function, here we show that these descriptions are consistent with the attached-eddy model, which is formulated for the logarithmic region. Moreover, the attached-eddy model is used to derive the expected relations for all higher-order moments, leading to the prediction that all even moments will follow a logarithmic dependence with
$\ln (r/z)$
range of the second-order structure function, here we show that these descriptions are consistent with the attached-eddy model, which is formulated for the logarithmic region. Moreover, the attached-eddy model is used to derive the expected relations for all higher-order moments, leading to the prediction that all even moments will follow a logarithmic dependence with
![]() $r/z$
of the form
$r/z$
of the form
and this is strongly supported by the experimental results for
![]() $2p=2{-}10$
.
$2p=2{-}10$
.
In the inertial subrange, the experimental data also show strong support for a power-law scaling, where the scaling exponent
![]() ${\it\xi}_{2p}$
is shown to match well with prior data (Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). Further, estimates for the multiplicative constant
${\it\xi}_{2p}$
is shown to match well with prior data (Anselmet et al.
Reference Anselmet, Gagne, Hopfinger and Antonia1984; Sreenivasan & Antonia Reference Sreenivasan and Antonia1997). Further, estimates for the multiplicative constant
![]() $M_{p}$
are presented up to the 10th moment for structure functions, with good agreement observed across all datasets. The transition length scale
$M_{p}$
are presented up to the 10th moment for structure functions, with good agreement observed across all datasets. The transition length scale
![]() $L_{s}$
, studied extensively for shear flows in prior work, is shown to demarcate regions of the structure function with differing scaling behaviour, where a transition from a power law at scales smaller than
$L_{s}$
, studied extensively for shear flows in prior work, is shown to demarcate regions of the structure function with differing scaling behaviour, where a transition from a power law at scales smaller than
![]() $L_{s}$
to a log-law behaviour at larger scales is observed.
$L_{s}$
to a log-law behaviour at larger scales is observed.
The employment of both spatial and temporal datasets enabled us to compute structure functions with and without invoking Taylor’s frozen turbulence hypothesis. Our findings show consistent results, highlighting that Taylor’s frozen turbulence hypothesis can be used to compute structure functions from temporal data at least up to
![]() $r=O({\it\delta})$
. An empirically based approach to model the scaling coefficients within the
$r=O({\it\delta})$
. An empirically based approach to model the scaling coefficients within the
![]() $\ln (r/z)$
range based on the inertial subrange constants is also presented. Estimates from this model are shown to match well with results computed directly from experimental datasets.
$\ln (r/z)$
range based on the inertial subrange constants is also presented. Estimates from this model are shown to match well with results computed directly from experimental datasets.
The analysis presented in this paper highlights the universality of the structure function as a tool to understand the scaling behaviour within the logarithmic region of turbulent boundary layers. The consistency in scaling regimes observed in the structure functions from this study complements the findings of Meneveau & Marusic (Reference Meneveau and Marusic2013) on the higher moments of the streamwise velocity fluctuations, and provides further statistical information to test the accuracy of both experimental datasets and simulations beyond tests that are usually considered using lower-order statistics.
Acknowledgements
The authors gratefully acknowledge the financial support of the Australian Research Council. C.M. is grateful to the Australian–American Fulbright Commission Senior Scholar Fellowship program for support during initial stages of this work, and the US National Science Foundation (grants CBET 1133800 and IIA 124382) for subsequent support.
Appendix A. Derivation of the functional forms of the structure functions via the attached-eddy model
In this appendix, we present the derivation of the functional forms of the structure functions that are referenced in § 5.2, where we noted that Campbell’s theorem reduces the derivation of the structure function to an integral over two identical eddies that are opposite in sign and separated by a distance
![]() $R$
. Which pairs of eddies will make a non-negligible contribution to the flow will depend upon two separate and contradictory concerns. If the eddies are too small (i.e. if
$R$
. Which pairs of eddies will make a non-negligible contribution to the flow will depend upon two separate and contradictory concerns. If the eddies are too small (i.e. if
![]() $Z$
is too large), their contributions to the velocity field may not extend to
$Z$
is too large), their contributions to the velocity field may not extend to
![]() $z$
. If, however, the eddies are too large (or
$z$
. If, however, the eddies are too large (or
![]() $R$
is too small), the velocity fields corresponding to the two eddies will overlap, causing a reduction in the magnitude of
$R$
is too small), the velocity fields corresponding to the two eddies will overlap, causing a reduction in the magnitude of
![]() $Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)-Q_{x}(\boldsymbol{X})$
, and thereby any even-ordered structure functions.
$Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)-Q_{x}(\boldsymbol{X})$
, and thereby any even-ordered structure functions.
The derivation of the structure function is largely analogous to the derivation of the moments of the velocity presented by Woodcock & Marusic (Reference Woodcock and Marusic2015). Hence, the derivation of
![]() $\langle {\rm\Delta}u_{+}^{n}\rangle$
can be found by making the following substitutions within that work:
$\langle {\rm\Delta}u_{+}^{n}\rangle$
can be found by making the following substitutions within that work:
The streamwise velocity corresponding to two such eddies can be seen in figure 13 for eddies of various heights. There it can be seen that if the ratio
![]() $R$
is sufficiently large, the velocity fields corresponding to the two eddies are effectively independent. Conversely, if
$R$
is sufficiently large, the velocity fields corresponding to the two eddies are effectively independent. Conversely, if
![]() $R$
is sufficiently small, the velocity fields corresponding to the two eddies will overlap, and begin to cancel each other out.
$R$
is sufficiently small, the velocity fields corresponding to the two eddies will overlap, and begin to cancel each other out.

Figure 13. Graphical representation of the velocity difference function,
![]() ${\rm\Delta}Q_{x}(\boldsymbol{X},R)=Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)-Q_{x}(\boldsymbol{X})$
, for different eddy heights. (This graph is merely a heuristic guide, and is not intended to represent the exact shape of
${\rm\Delta}Q_{x}(\boldsymbol{X},R)=Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)-Q_{x}(\boldsymbol{X})$
, for different eddy heights. (This graph is merely a heuristic guide, and is not intended to represent the exact shape of
![]() ${\rm\Delta}Q_{x}$
.)
${\rm\Delta}Q_{x}$
.)
Rather than attempt to account for both of these issues simultaneously, we instead deal with them independently. To do so, we first consider the case in which
![]() $r$
is sufficiently large that none of the eddies overlap. In this special case the eddy difference contribution defined in (5.12) reduces to
$r$
is sufficiently large that none of the eddies overlap. In this special case the eddy difference contribution defined in (5.12) reduces to
 $$\begin{eqnarray}{\rm\Delta}I_{k}(\boldsymbol{X},R)=\left\{\begin{array}{@{}ll@{}}\displaystyle \iint _{-\infty }^{\infty }2Q_{x}^{k}(\boldsymbol{X})\text{d}X\text{d}Y,\quad & \text{for }k\text{ even},\\ 0,\quad & \text{for }k\text{ odd},\end{array}\right.\quad \text{for }r\gg h_{max}.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}I_{k}(\boldsymbol{X},R)=\left\{\begin{array}{@{}ll@{}}\displaystyle \iint _{-\infty }^{\infty }2Q_{x}^{k}(\boldsymbol{X})\text{d}X\text{d}Y,\quad & \text{for }k\text{ even},\\ 0,\quad & \text{for }k\text{ odd},\end{array}\right.\quad \text{for }r\gg h_{max}.\end{eqnarray}$$
The value of
![]() ${\it\Lambda}_{2n}$
is derived from the above
${\it\Lambda}_{2n}$
is derived from the above
![]() ${\rm\Delta}I_{2n}$
via (5.13). It has previously been shown by Woodcock & Marusic (Reference Woodcock and Marusic2015) that so long as
${\rm\Delta}I_{2n}$
via (5.13). It has previously been shown by Woodcock & Marusic (Reference Woodcock and Marusic2015) that so long as
![]() $z\ll h_{max}$
a logarithmic dependence upon
$z\ll h_{max}$
a logarithmic dependence upon
![]() $z$
will be exhibited. In fact, this can be re-expressed in terms of the function
$z$
will be exhibited. In fact, this can be re-expressed in terms of the function
![]() ${\it\lambda}_{k}$
, which is defined in equation (19) of that article. It is given by
${\it\lambda}_{k}$
, which is defined in equation (19) of that article. It is given by
We can account for the effect on
![]() ${\rm\Delta}I_{2n}$
of any overlap between
${\rm\Delta}I_{2n}$
of any overlap between
![]() $Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
and
$Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
and
![]() $Q_{x}(\boldsymbol{X})$
by including an additional term,
$Q_{x}(\boldsymbol{X})$
by including an additional term,
![]() ${\it\zeta}_{k}(\boldsymbol{X},R)$
, to account for any overlapping that occurs at low
${\it\zeta}_{k}(\boldsymbol{X},R)$
, to account for any overlapping that occurs at low
![]() $R$
. The eddy difference contribution becomes
$R$
. The eddy difference contribution becomes
 $$\begin{eqnarray}{\rm\Delta}I_{k}(\boldsymbol{X},R)=\left\{\begin{array}{@{}ll@{}}\displaystyle \iint _{-\infty }^{\infty }2Q_{x}^{k}(\boldsymbol{X})\text{d}X\text{d}Y-{\it\zeta}_{k},\quad & \text{for }k\text{ even},\\ -{\it\zeta}_{k},\quad & \text{for }k\text{ odd}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\rm\Delta}I_{k}(\boldsymbol{X},R)=\left\{\begin{array}{@{}ll@{}}\displaystyle \iint _{-\infty }^{\infty }2Q_{x}^{k}(\boldsymbol{X})\text{d}X\text{d}Y-{\it\zeta}_{k},\quad & \text{for }k\text{ even},\\ -{\it\zeta}_{k},\quad & \text{for }k\text{ odd}.\end{array}\right.\end{eqnarray}$$
By substituting (A 4) into (5.13), we retrieve
 $$\begin{eqnarray}{\it\Lambda}_{k}(z,r)=\left\{\begin{array}{@{}ll@{}}2{\it\lambda}_{k}(z)-{\it\beta}\displaystyle \int _{h_{min}}^{h_{max}}{\it\zeta}_{k}(\boldsymbol{X},R)h^{2}P(h)\text{d}h,\quad & \text{for }k\text{ even},\\ -{\it\beta}\displaystyle \int _{h_{min}}^{h_{max}}{\it\zeta}_{k}(\boldsymbol{X},R)h^{2}P(h)\text{d}h,\quad & \text{for }k\text{ odd}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\Lambda}_{k}(z,r)=\left\{\begin{array}{@{}ll@{}}2{\it\lambda}_{k}(z)-{\it\beta}\displaystyle \int _{h_{min}}^{h_{max}}{\it\zeta}_{k}(\boldsymbol{X},R)h^{2}P(h)\text{d}h,\quad & \text{for }k\text{ even},\\ -{\it\beta}\displaystyle \int _{h_{min}}^{h_{max}}{\it\zeta}_{k}(\boldsymbol{X},R)h^{2}P(h)\text{d}h,\quad & \text{for }k\text{ odd}.\end{array}\right.\end{eqnarray}$$
The value of
![]() ${\it\zeta}_{k}(\boldsymbol{X},R)$
can easily be derived by expanding the brackets in (5.12). For example, we can see that the second-order term is
${\it\zeta}_{k}(\boldsymbol{X},R)$
can easily be derived by expanding the brackets in (5.12). For example, we can see that the second-order term is
Higher-order terms will of course contain more components, but what is important is that they will all contain a power of
![]() $Q_{x}(\boldsymbol{X})$
multiplied by a power of
$Q_{x}(\boldsymbol{X})$
multiplied by a power of
![]() $Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
. Their exact forms are trivial to determine, but are not necessary for the following derivation.
$Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
. Their exact forms are trivial to determine, but are not necessary for the following derivation.
What is important, however, is that a cursory glance at (5.12) reveals that at
![]() $R=0$
,
$R=0$
,
The importance of this will be revealed subsequently. The reason for introducing
![]() ${\it\zeta}_{k}(\boldsymbol{X},R)$
is that it becomes small when either
${\it\zeta}_{k}(\boldsymbol{X},R)$
is that it becomes small when either
![]() $Z$
or
$Z$
or
![]() $R$
is large. We therefore need only exclude eddies that are too small for a given
$R$
is large. We therefore need only exclude eddies that are too small for a given
![]() $r$
and
$r$
and
![]() $z$
. It is clear that the
$z$
. It is clear that the
![]() $r$
dependence of
$r$
dependence of
![]() ${\it\zeta}_{k}$
is functionally similar to its
${\it\zeta}_{k}$
is functionally similar to its
![]() $z$
dependence in that there will exist a value of
$z$
dependence in that there will exist a value of
![]() $r$
beyond which
$r$
beyond which
![]() ${\it\zeta}_{k}$
will be negligible, and that this value will be proportional to
${\it\zeta}_{k}$
will be negligible, and that this value will be proportional to
![]() $h$
. (It is not particularly important what we define to be ‘negligible’, so long as we are consistent with this definition.) It must be noted, however, that if
$h$
. (It is not particularly important what we define to be ‘negligible’, so long as we are consistent with this definition.) It must be noted, however, that if
![]() $Q_{x}(\boldsymbol{X})$
becomes negligible at
$Q_{x}(\boldsymbol{X})$
becomes negligible at
![]() $r=r^{\prime }$
, then
$r=r^{\prime }$
, then
![]() $Q_{x}(\boldsymbol{X})Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
will only become negligible at
$Q_{x}(\boldsymbol{X})Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
will only become negligible at
![]() $r=2r^{\prime }$
. This is illustrated in figure 14.
$r=2r^{\prime }$
. This is illustrated in figure 14.

Figure 14. Diagram showing
![]() $Q_{x}(\boldsymbol{X})$
and
$Q_{x}(\boldsymbol{X})$
and
![]() $Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
. Here, it can be seen that if
$Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
. Here, it can be seen that if
![]() $Q_{x}$
becomes negligible at a distance of
$Q_{x}$
becomes negligible at a distance of
![]() $r^{\prime }$
from the centre of the eddy, then the product
$r^{\prime }$
from the centre of the eddy, then the product
![]() $Q_{x}(\boldsymbol{X})Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
can only be assumed to be universally zero if
$Q_{x}(\boldsymbol{X})Q_{x}(\boldsymbol{X}+\boldsymbol{i}R)$
can only be assumed to be universally zero if
![]() $r<2r^{\prime }$
.
$r<2r^{\prime }$
.
The Biot–Savart law indicates that the velocity field corresponding to a spatially limited vorticity field will diminish as the distance from the vorticity field increases. While the rate at which the velocity field diminishes with distance may depend upon the direction, without knowing the nature of
![]() $\boldsymbol{Q}(\boldsymbol{X})$
, this is impossible to specify. We do know, however, from the Biot–Savart law that at sufficient distance from the eddy,
$\boldsymbol{Q}(\boldsymbol{X})$
, this is impossible to specify. We do know, however, from the Biot–Savart law that at sufficient distance from the eddy,
![]() $l$
,
$l$
,
Importantly, the magnitude of
![]() $Q_{x}(l/h)$
begins to diminish at the same rate regardless of the direction of the displacement. This will allow us to account for
$Q_{x}(l/h)$
begins to diminish at the same rate regardless of the direction of the displacement. This will allow us to account for
![]() $r$
and
$r$
and
![]() $z$
simultaneously.
$z$
simultaneously.
In this case, the equivalent of
![]() $l$
would be
$l$
would be
In this way, we can redefine
![]() $z$
and
$z$
and
![]() $r$
in a form of polar coordinates. Our angular coordinate,
$r$
in a form of polar coordinates. Our angular coordinate,
![]() ${\it\theta}$
, is defined such that
${\it\theta}$
, is defined such that
We can similarly scale this distance with the height of the eddy, so that
From (A 8), we can see that for sufficiently high
![]() $l$
, if we define
$l$
, if we define
![]() $\hat{{\it\zeta}}_{k}(L,{\it\theta})\equiv {\it\zeta}_{k}(\boldsymbol{X},R)$
, then
$\hat{{\it\zeta}}_{k}(L,{\it\theta})\equiv {\it\zeta}_{k}(\boldsymbol{X},R)$
, then
where
![]() $f({\it\theta})$
represents the fact that the velocity field may diminish faster with
$f({\it\theta})$
represents the fact that the velocity field may diminish faster with
![]() $z$
than with
$z$
than with
![]() $r$
. It should be noted that if
$r$
. It should be noted that if
![]() $r\gg z$
, then
$r\gg z$
, then
![]() ${\it\theta}$
, and hence
${\it\theta}$
, and hence
![]() $f({\it\theta})$
, will change negligibly with
$f({\it\theta})$
, will change negligibly with
![]() $r$
.
$r$
.
Hence, in the
![]() $r\gg z$
case, we can simply say that
$r\gg z$
case, we can simply say that
A.1. Even-ordered cumulants
We are now able to follow a very similar derivation to that presented by Woodcock & Marusic (Reference Woodcock and Marusic2015) in order to derive the even-ordered cumulants,
![]() ${\it\Lambda}_{2n}$
. First, we rewrite (A 5) as
${\it\Lambda}_{2n}$
. First, we rewrite (A 5) as
If we assume that there exists a number
![]() ${\it\eta}$
such that if
${\it\eta}$
such that if
![]() $l/h>{\it\eta}$
,
$l/h>{\it\eta}$
,
![]() ${\it\zeta}_{k}$
will be negligible, we therefore say that
${\it\zeta}_{k}$
will be negligible, we therefore say that
Because
![]() $\hat{{\it\zeta}}_{k}$
is assumed to be non-zero only if
$\hat{{\it\zeta}}_{k}$
is assumed to be non-zero only if
![]() $l/{\it\eta}<h\leqslant h_{max}$
, we need not integrate from
$l/{\it\eta}<h\leqslant h_{max}$
, we need not integrate from
![]() $h_{min}$
to
$h_{min}$
to
![]() $h_{max}$
in (5.13). Therefore, (5.13) can be written as
$h_{max}$
in (5.13). Therefore, (5.13) can be written as
 $$\begin{eqnarray}{\it\Lambda}_{2n}(z,r)=\left\{\begin{array}{@{}ll@{}}2{\it\lambda}_{2n}(z)-{\it\beta}\displaystyle \int _{l/{\it\eta}}^{h_{max}}\hat{{\it\zeta}}_{2n}\left(L\right)h^{2}P(h)\text{d}h,\quad & \text{for }l>{\it\eta}h_{min},\\ 2{\it\lambda}_{2n}(z)-{\it\beta}\displaystyle \int _{h_{min}}^{h_{max}}\hat{{\it\zeta}}_{2n}\left(L\right)h^{2}P(h)\text{d}h,\quad & \text{for }l\leqslant {\it\eta}h_{min}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}{\it\Lambda}_{2n}(z,r)=\left\{\begin{array}{@{}ll@{}}2{\it\lambda}_{2n}(z)-{\it\beta}\displaystyle \int _{l/{\it\eta}}^{h_{max}}\hat{{\it\zeta}}_{2n}\left(L\right)h^{2}P(h)\text{d}h,\quad & \text{for }l>{\it\eta}h_{min},\\ 2{\it\lambda}_{2n}(z)-{\it\beta}\displaystyle \int _{h_{min}}^{h_{max}}\hat{{\it\zeta}}_{2n}\left(L\right)h^{2}P(h)\text{d}h,\quad & \text{for }l\leqslant {\it\eta}h_{min}.\end{array}\right.\end{eqnarray}$$
If we take the
![]() $l>{\it\eta}h_{min}$
case in the above equation, and substitute (5.14) for
$l>{\it\eta}h_{min}$
case in the above equation, and substitute (5.14) for
![]() $P(h)$
, it can be rewritten as
$P(h)$
, it can be rewritten as
In order to derive the functional form of the structure function from the above equation we first recognise that a major contribution to the integral above will emanate from near
![]() $L=0$
. This, coupled with the fact that
$L=0$
. This, coupled with the fact that
![]() $\hat{{\it\zeta}}_{2n}\left(L\right)$
will at some point begin to diminish as
$\hat{{\it\zeta}}_{2n}\left(L\right)$
will at some point begin to diminish as
![]() $L$
increases, indicates that it is reasonable to expand
$L$
increases, indicates that it is reasonable to expand
![]() $\hat{{\it\zeta}}_{2n}$
in a Taylor series around
$\hat{{\it\zeta}}_{2n}$
in a Taylor series around
![]() $L=0$
. This gives
$L=0$
. This gives
If
![]() $l\ll h_{max}$
, it is the first term in this expansion that will dominate within the integral. We can therefore say that
$l\ll h_{max}$
, it is the first term in this expansion that will dominate within the integral. We can therefore say that
We may further simplify this result by recognising that
![]() $\hat{{\it\zeta}}_{k}$
may be related to the eddy contribution function
$\hat{{\it\zeta}}_{k}$
may be related to the eddy contribution function
![]() $I_{k,0,0}$
, which was defined by Woodcock & Marusic (Reference Woodcock and Marusic2015) and is given in equation (18) of that work. From (A 7) of the present paper, we can see that
$I_{k,0,0}$
, which was defined by Woodcock & Marusic (Reference Woodcock and Marusic2015) and is given in equation (18) of that work. From (A 7) of the present paper, we can see that
By taking into account equation (38) of Woodcock & Marusic (Reference Woodcock and Marusic2015), we can see that
where
![]() $\mathscr{A}_{k}$
and
$\mathscr{A}_{k}$
and
![]() $\mathscr{C}_{k}$
are constants, and
$\mathscr{C}_{k}$
are constants, and
![]() $\mathscr{A}_{k}$
is given by
$\mathscr{A}_{k}$
is given by
Because the boundary conditions applied within the attached-eddy model are starkly different from the no-slip boundary conditions that apply to real turbulent flows, we cannot derive a realistic approximation for
![]() $\mathscr{C}_{k}$
via this method. Therefore, although we could derive an equivalent expression to the above for
$\mathscr{C}_{k}$
via this method. Therefore, although we could derive an equivalent expression to the above for
![]() $\mathscr{C}_{k}$
, we elect not to do so.
$\mathscr{C}_{k}$
, we elect not to do so.
Of course, since we have already made the important assumption that
![]() $r\gg z$
, the above expression for
$r\gg z$
, the above expression for
![]() ${\it\Lambda}_{k}(z,r)$
can be easily simplified to
${\it\Lambda}_{k}(z,r)$
can be easily simplified to
where
![]() $\mathscr{B}_{k}$
is a constant. It should be noted that
$\mathscr{B}_{k}$
is a constant. It should be noted that
![]() $\mathscr{C}_{k}$
in (A 21a
) has been replaced by
$\mathscr{C}_{k}$
in (A 21a
) has been replaced by
![]() $\mathscr{B}_{k}$
in the above equation. This is because the value of the additive constant has been altered. This expression concurs with that given by Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
).
$\mathscr{B}_{k}$
in the above equation. This is because the value of the additive constant has been altered. This expression concurs with that given by Davidson et al. (Reference Davidson, Nickels and Krogstad2006b
).
A.2. Odd-ordered cumulants
The derivation of the odd-ordered cumulants progresses via an entirely analogous path to their even-ordered counterparts, with the important exception that (A 5) and (A 7) take very different forms.
The important implication of (A 7) is that
By proceeding in the same manner as in the even-ordered case, we find that if
![]() $l\ll h_{max}$
,
$l\ll h_{max}$
,
Using (A 5), this becomes
A comparison with the scaling behaviour derived here for the odd-order structure functions shows results that compare favourably with those measured experimentally. An in-depth presentation and analysis of odd-order moments is relegated to a future communication since this paper is focused on even-order moments.