Article contents
Bounding Sn(t) on the Riemann hypothesis
Published online by Cambridge University Press: 02 March 2017
Abstract
Let 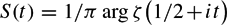 $S(t) = {1}/{\pi} \arg \zeta \big(\hh + it \big)$ be the argument of the Riemann zeta-function at the point 1/2 + it. For n ⩾ 1 and t > 0 define its iterates
$S(t) = {1}/{\pi} \arg \zeta \big(\hh + it \big)$ be the argument of the Riemann zeta-function at the point 1/2 + it. For n ⩾ 1 and t > 0 define its iterates
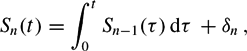 $$\begin{equation*}
S_n(t) = \int_0^t S_{n-1}(\tau) \,\d\tau\, + \delta_n\,,
\end{equation*}$$
$$\begin{equation*}
S_n(t) = \int_0^t S_{n-1}(\tau) \,\d\tau\, + \delta_n\,,
\end{equation*}$$
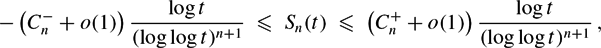 $$\begin{equation*}
-\left( C^-_n + o(1)\right) \frac{\log t}{(\log \log t)^{n+1}} \ \leq \ S_n(t) \ \leq \ \left( C^+_n + o(1)\right) \frac{\log t}{(\log \log t)^{n+1}}\,,
\end{equation*}$$
$$\begin{equation*}
-\left( C^-_n + o(1)\right) \frac{\log t}{(\log \log t)^{n+1}} \ \leq \ S_n(t) \ \leq \ \left( C^+_n + o(1)\right) \frac{\log t}{(\log \log t)^{n+1}}\,,
\end{equation*}$$
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 164 , Issue 2 , March 2018 , pp. 259 - 283
- Copyright
- Copyright © Cambridge Philosophical Society 2017
References
REFERENCES
- 8
- Cited by




