Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-19T19:44:53.075Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SPECTRAL TYPE OF SUMS OF OPERATORS ON NON-HILBERTIAN BANACH LATTICES

Part of: Special classes of linear operators

Published online by Cambridge University Press:  01 April 2008

IAN DOUST  and
GILLES LANCIEN
IAN DOUST*
Affiliation:
School of Mathematics, University of New South Wales, Sydney, NSW 2052, Australia (email: i.doust@unsw.edu.au)
GILLES LANCIEN
Affiliation:
Equipe de Mathématiques UMR 6623, Université de Franche-Comté, F-25030 Besançon cedex, France (email: gilles.lancien@math.univ-fcomte.fr)
*
✉For correspondence; e-mail: i.doust@unsw.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

T. A. Gillespie showed that on a Hilbert space the sum of a well-bounded operator and a commuting real scalar-type spectral operator is well-bounded. A longstanding question asked whether this might still hold true for operators on Lp spaces for 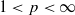. We show here that this conjecture is false. Indeed for a large class of reflexive spaces, the above property characterizes Hilbert space.

Keywords

well-bounded operatorsscalar-type spectral operatorsfunctional calculus

MSC classification

Secondary: 47B40: Spectral operators, decomposable operators, well-bounded operators, etc.
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 84 , Issue 2 , April 2008 , pp. 193 - 198
Copyright
Copyright © 2008 Australian Mathematical Society

References

[1]Cheng, Q. and Doust, I., ‘Compact well-bounded operators’, Glasg. Math. J. 43 (2001), 457–467.Google Scholar
[2]Doust, I. and Gillespie, T. A., ‘Well-boundedness of sums and products of operators’, J. London Math. Soc. (2) 68 (2003), 183–192.CrossRefGoogle Scholar
[3]Doust, I., Lancien, F. and Lancien, G., ‘Spectral theory for linear operators on L 1 or C(K) spaces’, in: Asymptotic geometric analysis, harmonic analysis, and related topics (Murramarang 2006), Proceedings of the Centre for Mathematics and its Applications, Australian National University, 42 (Australian National University, Canberra, 2007), pp. 1–10.Google Scholar
[4]Dowson, H. R., Spectral Theory of Linear Operators, London Mathematical Society Monographs, 12 (Academic Press, London, 1978).Google Scholar
[5]Gillespie, T. A., ‘Commuting well-bounded operators on Hilbert spaces’, Proc. Edinb. Math. Soc. (2) 20 (1976), 167–172.CrossRefGoogle Scholar
[6]Gillespie, T. A., ‘Boundedness criteria for Boolean algebras of projections’, J. Funct. Anal. 148 (1997), 70–85.CrossRefGoogle Scholar
[7]Kalton, N. J. and Lancien, G., ‘A solution to the problem of L p-maximal regularity’, Math. Z. 235 (2000), 559–568.CrossRefGoogle Scholar
[8]Kalton, N. J. and Weis, L., ‘The -calculus and sums of closed operators’, Math. Ann. 321 (2001), 319–345.CrossRefGoogle Scholar
[9]Lindenstrauss, J. and Tzafriri, L., ‘On the complemented subspaces problem’, Israel J. Math. 9 (1971), 263–269.CrossRefGoogle Scholar
[10]Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces I (Springer, Berlin, 1977).CrossRefGoogle Scholar
[11]Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces II (Springer, Berlin, 1979).CrossRefGoogle Scholar
[12]Lindenstrauss, J. and Zippin, M., ‘Banach spaces with unique unconditional basis’, J. Funct. Anal. 3 (1969), 115–125.CrossRefGoogle Scholar
[13]McCarthy, C. A., ‘Commuting Boolean algebras of projections’, Pacific J. Math. 11 (1961), 295–307.CrossRefGoogle Scholar
[14]McCarthy, C. A., ‘Commuting Boolean algebras of projections. II. Boundedness in L p’, Proc. Amer. Math. Soc. 15 (1964), 781–787.Google Scholar
[15]Ricker, W., ‘Spectral operators of scalar type in Grothendieck spaces with the Dunford–Pettis property’, Bull. London Math. Soc. 17 (1985), 268–270.CrossRefGoogle Scholar