Hostname: page-component-8448b6f56d-dnltx Total loading time: 0 Render date: 2024-04-16T20:31:12.159Z Has data issue: false hasContentIssue false
  • English
  • Français

On convex sets that minimize the average distance

Published online by Cambridge University Press:  16 January 2012

Antoine Lemenant  and
Edoardo Mainini
Antoine Lemenant
Affiliation:
UniversitéParis Diderot – Paris 7, U.F.R de Mathématiques, Site Chevaleret, Case 7012, 75205 Paris Cedex 13, France. lemenant@ann.jussieu.fr
Edoardo Mainini
Affiliation:
Dipartimento di Matematica ‘F. Casorati’, Universià degli Studi di Pavia, via Ferrata 1, 27100 Pavia, Italy; edoardo.mainini@unipv.it
Get access

Abstract

In this paper we study the compact and convex sets K ⊆ Ω ⊆ ℝ2 that minimize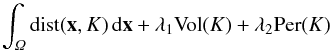

\begin{equation*} \int_{\Omega} \dist(\x,K) \,{\rm d}\x + \lambda_1 {\rm Vol}(K)+\lambda_2 {\rm Per}(K) \end{equation*}∫Ωdist(x,K)dx+λ1Vol(K)+λ2Per(K)
for some constants λ1 and λ2, that could possibly be zero. We compute in particular the second order derivative of the functional and use it to exclude smooth points of positive curvature for the problem with volume constraint. The problem with perimeter constraint behaves differently since polygons are never minimizers. Finally using a purely geometrical argument from Tilli [J. Convex Anal. 17 (2010) 583–595] we can prove that any arbitrary convex set can be a minimizer when both perimeter and volume constraints are considered.

Keywords

Shape optimizationdistance functionaloptimality conditionsconvex analysissecond order variationgamma-convergence
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 18 , Issue 4 , October 2012 , pp. 1049 - 1072
Copyright
© EDP Sciences, SMAI, 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, L. and Mantegazza, C., Curvature and distance function from a manifold. J. Geom. Anal. 8 (1998) 723–748. Dedicated to the memory of Fred Almgren. Google Scholar
Ambrosio, L. and Tortorelli, V.M., Approximation of functionals depending on jumps by elliptic functionals via Γ-convergence. Comm. Pure Appl. Math. 43 (1990) 999–1036. Google Scholar
D. Bucur, I. Fragalà and J. Lamboley, Optimal convex shapes for concave functionals. ESAIM : COCV (in press).
Buttazzo, G. and Guasoni, P., Shape optimization problems over classes of convex domains. J. Convex Anal. 4 (1997) 343–351. Google Scholar
Buttazzo, G. and Santambrogio, F., Asymptotical compliance optimization for connected networks. Netw. Heterog. Media 2 (2007) 761–777 (electronic). Google Scholar
Buttazzo, G. and Stepanov, E., Optimal transportation networks as free Dirichlet regions for the Monge-Kantorovich problem. Ann. Scuola Norm. Super. Pisa Cl. Sci. 2 (2003) 631–678. Google Scholar
G. Buttazzo, E. Oudet and E. Stepanov, Optimal transportation problems with free Dirichlet regions, in Variational methods for discontinuous structures, Progr. Nonlinear Differential Equations Appl. 51. Birkhäuser, Basel (2002) 41–65.
G. Buttazzo, A. Pratelli, S. Solimini and E. Stepanov, Optimal urban networks via mass transportation, Lecture Notes in Mathematics 1961. Springer-Verlag, Berlin (2009).
Buttazzo, G., Mainini, E. and Stepanov, E., Stationary configurations for the average distance functional and related problems. Control Cybernet. 38 (2009) 1107–1130. Google Scholar
M.C. Delfour and J.-P. Zolésio, Shape analysis via distance functions : local theory, in Boundaries, interfaces, and transitions (Banff, AB, 1995), CRM Proc. Lect. Notes 13. Amer. Math. Soc. Providence, RI (1998) 91–123.
Federer, H., Curvature measures. Trans. Amer. Math. Soc. 93 (1959) 418–491. Google Scholar
H. Federer, Geometric measure theory, Die Grundlehren der mathematischen Wissenschaften, Band 153. Springer-Verlag New York Inc., New York (1969).
A. Henrot and M. Pierre, Variation et optimisation de formes, Mathématiques & Applications (Berlin) [Mathematics & Applications] 48. Springer, Berlin (2005). Une analyse géométrique [a geometric analysis].
Lemenant, A., About the regularity of average distance minimizers in R2. J. Convex Anal. 18 (2011) 949–981. Google Scholar
A. Lemenant, A presentation of the average distance minimizing problem. Zap. Nauchn. Sem. S.-Petersburg. Otdel. Mat. Inst. Steklov. (POMI) 390 (2010) 117–146 (Proceedings of St. Petersburg Seminar, available online at http://www.pdmi.ras.ru/znsl/2011/v390/abs117.html).
Mantegazza, C. and Mennucci, A., Hamilton-jacobi equations and distance functions on riemannian manifolds. Appl. Math. Optim. 47 (2003) 1–25. Google Scholar
Modica, L. and Mortola, S., Il limite nella Γ-convergenza di una famiglia di funzionali ellittici. Boll. Un. Mat. Ital. A 14 (1977) 526–529. Google Scholar
Paolini, E. and Stepanov, E., Qualitative properties of maximum distance minimizers and average distance minimizers in Rn. J. Math. Sci. (N. Y.) 122 (2004) 3290–3309. Problems in mathematical analysis. Google Scholar
Santambrogio, F. and Tilli, P., Blow-up of optimal sets in the irrigation problem. J. Geom. Anal. 15 (2005) 343–362. Google Scholar
L. Simon, Lectures on geometric measure theory, Proceedings of the Centre for Mathematical Analysis 3. Australian National University, Australian National University Centre for Mathematical Analysis, Canberra (1983).
Stepanov, E., Partial geometric regularity of some optimal connected transportation networks. J. Math. Sci. (N.Y.) 132 (2006) 522–552. Problems in mathematical analysis. Google Scholar
Tilli, P., Some explicit examples of minimizers for the irrigation problem. J. Convex Anal. 17 (2010) 583–595. Google Scholar