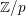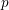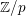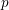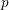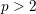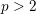1 Introduction
The (birational) (
![]() $p$
-adic) section conjecture (SC) originates from Grothendieck [Reference GrothendieckGro83, Reference GrothendieckGro84] (see [Reference Schneps and LochakSL98]), and weaker/conditional forms of the SC are a part of the local theory in anabelian geometry, see e.g. Faltings [Reference FaltingsFal98] and Szamuely [Reference SzamuelySza04]. In spite of serious efforts to tackle the SC, only the full Galois birational
$p$
-adic) section conjecture (SC) originates from Grothendieck [Reference GrothendieckGro83, Reference GrothendieckGro84] (see [Reference Schneps and LochakSL98]), and weaker/conditional forms of the SC are a part of the local theory in anabelian geometry, see e.g. Faltings [Reference FaltingsFal98] and Szamuely [Reference SzamuelySza04]. In spite of serious efforts to tackle the SC, only the full Galois birational
![]() $p$
-adic SC is completely resolved, see Koenigsmann [Reference KoenigsmannKoe05] for the case of curves and Stix [Reference StixSti13] for higher dimensional varieties. On the other hand, a much stronger form of the birational
$p$
-adic SC is completely resolved, see Koenigsmann [Reference KoenigsmannKoe05] for the case of curves and Stix [Reference StixSti13] for higher dimensional varieties. On the other hand, a much stronger form of the birational
![]() $p$
-adic SC for curves, to be precise, the
$p$
-adic SC for curves, to be precise, the
![]() $\mathbb{Z}/p$
metabelian birational
$\mathbb{Z}/p$
metabelian birational
![]() $p$
-adic SC for curves, was proved in Pop [Reference PopPop10]. The aim of this note is to prove a similarly strong result for the higher dimensional varieties, at least in the case
$p$
-adic SC for curves, was proved in Pop [Reference PopPop10]. The aim of this note is to prove a similarly strong result for the higher dimensional varieties, at least in the case
![]() $p>2$
.
$p>2$
.
For the reader’s sake and to make the presentation self contained (to some extent), we begin by recalling a few notations and well-known facts; see e.g. the Introduction in [Reference PopPop10]. First, for an arbitrary (perfect) base field
![]() $k$
and complete smooth geometrically integral
$k$
and complete smooth geometrically integral
![]() $k$
-varieties
$k$
-varieties
![]() $X$
, let
$X$
, let
![]() $K=k(X)$
be the function field of
$K=k(X)$
be the function field of
![]() $X$
. Let
$X$
. Let
![]() $\tilde{K}|K$
be some Galois extension,
$\tilde{K}|K$
be some Galois extension,
![]() $\tilde{k}\subseteq \tilde{K}$
be the relative algebraic closure of
$\tilde{k}\subseteq \tilde{K}$
be the relative algebraic closure of
![]() $k$
in
$k$
in
![]() $\tilde{K}$
, and consider the resulting canonical exact sequence of Galois groups:
$\tilde{K}$
, and consider the resulting canonical exact sequence of Galois groups:
Let
![]() $\tilde{X}\rightarrow X$
be the normalization of
$\tilde{X}\rightarrow X$
be the normalization of
![]() $X$
in the field extension
$X$
in the field extension
![]() $K{\hookrightarrow}\tilde{K}$
. For
$K{\hookrightarrow}\tilde{K}$
. For
![]() $x\in X$
and
$x\in X$
and
![]() $\tilde{x}\in \tilde{X}$
above
$\tilde{x}\in \tilde{X}$
above
![]() $x$
, let
$x$
, let
![]() $T_{x}\subseteq Z_{x}$
be the inertia/decomposition groups of
$T_{x}\subseteq Z_{x}$
be the inertia/decomposition groups of
![]() $\tilde{x}|x$
and
$\tilde{x}|x$
and
![]() $G_{x}:=\operatorname{Aut}(\unicode[STIX]{x1D705}(\tilde{x})|\unicode[STIX]{x1D705}(x))$
be the residual automorphism group. By decomposition theory, one has a canonical exact sequence
$G_{x}:=\operatorname{Aut}(\unicode[STIX]{x1D705}(\tilde{x})|\unicode[STIX]{x1D705}(x))$
be the residual automorphism group. By decomposition theory, one has a canonical exact sequence
Next suppose that
![]() $x$
is
$x$
is
![]() $k$
-rational, i.e.,
$k$
-rational, i.e.,
![]() $\unicode[STIX]{x1D705}(x)=k$
. Since
$\unicode[STIX]{x1D705}(x)=k$
. Since
![]() $\tilde{k}\subset \unicode[STIX]{x1D705}(\tilde{x})$
, the projection
$\tilde{k}\subset \unicode[STIX]{x1D705}(\tilde{x})$
, the projection
![]() $Z_{x}\xrightarrow[{}]{\tilde{p}_{K}}\operatorname{Gal}(\tilde{k}|k)$
gives rise to a canonical surjective homomorphism
$Z_{x}\xrightarrow[{}]{\tilde{p}_{K}}\operatorname{Gal}(\tilde{k}|k)$
gives rise to a canonical surjective homomorphism
![]() $G_{x}\rightarrow \operatorname{Gal}(\tilde{k}|k)$
, which in general is not injective. On the other hand, if
$G_{x}\rightarrow \operatorname{Gal}(\tilde{k}|k)$
, which in general is not injective. On the other hand, if
![]() $\tilde{k}{\hookrightarrow}\unicode[STIX]{x1D705}(\tilde{x})$
is purely inseparable, then
$\tilde{k}{\hookrightarrow}\unicode[STIX]{x1D705}(\tilde{x})$
is purely inseparable, then
![]() $G_{x}\rightarrow \operatorname{Gal}(\tilde{k}|k)$
is an isomorphism. Hence, if the sequence (∗) splits, then
$G_{x}\rightarrow \operatorname{Gal}(\tilde{k}|k)$
is an isomorphism. Hence, if the sequence (∗) splits, then
![]() $\tilde{p}_{K}$
has sections
$\tilde{p}_{K}$
has sections
![]() $\tilde{s}_{x}:\operatorname{Gal}(\tilde{k}|k)\rightarrow Z_{x}\subset \operatorname{Gal}(\tilde{K}|K)$
, which we call sections above
$\tilde{s}_{x}:\operatorname{Gal}(\tilde{k}|k)\rightarrow Z_{x}\subset \operatorname{Gal}(\tilde{K}|K)$
, which we call sections above
![]() $x$
. And, notice that the conjugacy classes of sections
$x$
. And, notice that the conjugacy classes of sections
![]() $\tilde{s}_{x}$
above
$\tilde{s}_{x}$
above
![]() $x$
build a ‘bouquet’, which is in a canonical bijection with the (non-commutative) continuous cohomology pointed set
$x$
build a ‘bouquet’, which is in a canonical bijection with the (non-commutative) continuous cohomology pointed set
![]() $\text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{x})$
defined via the split exact sequence (∗).
$\text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{x})$
defined via the split exact sequence (∗).
Parallel to the case of points
![]() $x\in X$
, one has a similar situation for
$x\in X$
, one has a similar situation for
![]() $k$
-valuations
$k$
-valuations
![]() $v$
of
$v$
of
![]() $K$
as follows. For any prolongation
$K$
as follows. For any prolongation
![]() $\tilde{v}$
of
$\tilde{v}$
of
![]() $v$
to
$v$
to
![]() $\tilde{K}$
, we denote by
$\tilde{K}$
, we denote by
![]() $T_{v}\subseteq Z_{v}$
the inertia/decomposition groups of
$T_{v}\subseteq Z_{v}$
the inertia/decomposition groups of
![]() $\tilde{v}|v$
and by
$\tilde{v}|v$
and by
![]() $G_{v}=Z_{v}/T_{v}$
the residual automorphism group. As above, if
$G_{v}=Z_{v}/T_{v}$
the residual automorphism group. As above, if
![]() $\unicode[STIX]{x1D705}(v)=k$
and
$\unicode[STIX]{x1D705}(v)=k$
and
![]() $\tilde{k}{\hookrightarrow}\unicode[STIX]{x1D705}(\tilde{v})$
is purely inseparable, one has: first, the canonical homomorphism
$\tilde{k}{\hookrightarrow}\unicode[STIX]{x1D705}(\tilde{v})$
is purely inseparable, one has: first, the canonical homomorphism
![]() $G_{v}\rightarrow \operatorname{Gal}(\tilde{k}|k)$
is an isomorphism. Second, if the exact sequence
$G_{v}\rightarrow \operatorname{Gal}(\tilde{k}|k)$
is an isomorphism. Second, if the exact sequence
![]() $1\rightarrow T_{v}\rightarrow Z_{v}\rightarrow G_{v}\rightarrow 1$
splits, then the projection
$1\rightarrow T_{v}\rightarrow Z_{v}\rightarrow G_{v}\rightarrow 1$
splits, then the projection
![]() $\tilde{p}_{K}:\operatorname{Gal}(\tilde{K}|K)\rightarrow \operatorname{Gal}(\tilde{k}|k)$
has a section
$\tilde{p}_{K}:\operatorname{Gal}(\tilde{K}|K)\rightarrow \operatorname{Gal}(\tilde{k}|k)$
has a section
![]() $\tilde{s}_{v}:\operatorname{Gal}(\tilde{k}|k)\rightarrow Z_{v}\subseteq \operatorname{Gal}(\tilde{K}|K)$
, which we call a section above
$\tilde{s}_{v}:\operatorname{Gal}(\tilde{k}|k)\rightarrow Z_{v}\subseteq \operatorname{Gal}(\tilde{K}|K)$
, which we call a section above
![]() $v$
. And, the conjugacy classes of sections
$v$
. And, the conjugacy classes of sections
![]() $\tilde{s}_{v}$
above
$\tilde{s}_{v}$
above
![]() $v$
build a ‘bouquet’, which is in a canonical bijection with the (non-commutative) continuous cohomology pointed set
$v$
build a ‘bouquet’, which is in a canonical bijection with the (non-commutative) continuous cohomology pointed set
![]() $\text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{v})$
defined via the canonical split exact sequence above.
$\text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{v})$
defined via the canonical split exact sequence above.
Finally, if
![]() $\tilde{K}|K$
contains a separable closure
$\tilde{K}|K$
contains a separable closure
![]() $K^{\text{s}}|K$
of
$K^{\text{s}}|K$
of
![]() $K$
and hence
$K$
and hence
![]() $\tilde{k}$
contains a corresponding separable closure
$\tilde{k}$
contains a corresponding separable closure
![]() $k^{\text{s}}$
of
$k^{\text{s}}$
of
![]() $k$
, then
$k$
, then
![]() $\unicode[STIX]{x1D705}(s)^{\text{s}}\subseteq \unicode[STIX]{x1D705}(\tilde{x}),\unicode[STIX]{x1D705}(\tilde{v})$
and
$\unicode[STIX]{x1D705}(s)^{\text{s}}\subseteq \unicode[STIX]{x1D705}(\tilde{x}),\unicode[STIX]{x1D705}(\tilde{v})$
and
![]() $G_{x}$
and
$G_{x}$
and
![]() $G_{v}$
are the absolute Galois groups of
$G_{v}$
are the absolute Galois groups of
![]() $\unicode[STIX]{x1D705}(x)$
and
$\unicode[STIX]{x1D705}(x)$
and
![]() $\unicode[STIX]{x1D705}(v)$
, respectively. Further, in this situation,
$\unicode[STIX]{x1D705}(v)$
, respectively. Further, in this situation,
![]() $1\rightarrow T_{v}\rightarrow Z_{v}\rightarrow G_{v}\rightarrow 1$
is split; see e.g. [Reference Kuhlmann, Pank and RoquetteKPR86]. Thus, if
$1\rightarrow T_{v}\rightarrow Z_{v}\rightarrow G_{v}\rightarrow 1$
is split; see e.g. [Reference Kuhlmann, Pank and RoquetteKPR86]. Thus, if
![]() $\unicode[STIX]{x1D705}(v)=k$
, sections above
$\unicode[STIX]{x1D705}(v)=k$
, sections above
![]() $v$
exist. In particular, if
$v$
exist. In particular, if
![]() $x\in X(k)$
is a
$x\in X(k)$
is a
![]() $k$
-rational point, then choosing
$k$
-rational point, then choosing
![]() $v$
such that
$v$
such that
![]() $\unicode[STIX]{x1D705}(x)=\unicode[STIX]{x1D705}(v)$
, it follows that sections above
$\unicode[STIX]{x1D705}(x)=\unicode[STIX]{x1D705}(v)$
, it follows that sections above
![]() $x$
exist as well, because every section above
$x$
exist as well, because every section above
![]() $v$
is a section above
$v$
is a section above
![]() $x$
as well. We mention though that in general the bouquet of sections above
$x$
as well. We mention though that in general the bouquet of sections above
![]() $x$
is much richer than the one of sections above
$x$
is much richer than the one of sections above
![]() $v$
. Namely, by general decomposition theory, one has
$v$
. Namely, by general decomposition theory, one has
![]() $T_{v}\subset T_{x}$
, and
$T_{v}\subset T_{x}$
, and
![]() $\text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{v})\rightarrow \text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{x})$
is a strict inclusion in general.
$\text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{v})\rightarrow \text{H}_{\text{cont}}^{1}(\operatorname{Gal}(\tilde{k}|k),T_{x})$
is a strict inclusion in general.
Next let
![]() $p$
be a fixed prime number. We denote by
$p$
be a fixed prime number. We denote by
![]() $K^{\prime }|K$
the (maximal)
$K^{\prime }|K$
the (maximal)
![]() $\mathbb{Z}/p$
elementary abelian extension of
$\mathbb{Z}/p$
elementary abelian extension of
![]() $K$
, and by
$K$
, and by
![]() $K^{\prime \prime }$
the maximal
$K^{\prime \prime }$
the maximal
![]() $\mathbb{Z}/p$
elementary abelian extension of
$\mathbb{Z}/p$
elementary abelian extension of
![]() $K^{\prime }$
(in some fixed algebraic closure of
$K^{\prime }$
(in some fixed algebraic closure of
![]() $K$
). Then
$K$
). Then
![]() $K^{\prime \prime }|K$
is a Galois extension, which we call the
$K^{\prime \prime }|K$
is a Galois extension, which we call the
![]() $\mathbb{Z}/p$
metabelian extension of
$\mathbb{Z}/p$
metabelian extension of
![]() $K$
, and its Galois group
$K$
, and its Galois group
![]() $\operatorname{Gal}(K^{\prime \prime }|K)$
is called the metabelian Galois group of
$\operatorname{Gal}(K^{\prime \prime }|K)$
is called the metabelian Galois group of
![]() $K$
. Note that
$K$
. Note that
![]() $k^{\prime }:=\overline{k}\cap K^{\prime }$
and
$k^{\prime }:=\overline{k}\cap K^{\prime }$
and
![]() $k^{\prime \prime }:=\overline{k}\cap K^{\prime \prime }$
are the
$k^{\prime \prime }:=\overline{k}\cap K^{\prime \prime }$
are the
![]() $\mathbb{Z}/p$
elementary abelian extension and the
$\mathbb{Z}/p$
elementary abelian extension and the
![]() $\mathbb{Z}/p$
metabelian extension, respectively, of
$\mathbb{Z}/p$
metabelian extension, respectively, of
![]() $k$
. Finally, consider the canonical surjective projections:
$k$
. Finally, consider the canonical surjective projections:
We will say that a group theoretical (continuous) section
![]() $s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
of
$s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
of
![]() $\operatorname{pr}_{K}^{\prime }$
is liftable if there exists a section
$\operatorname{pr}_{K}^{\prime }$
is liftable if there exists a section
![]() $s^{\prime \prime }:\operatorname{Gal}(k^{\prime \prime }|k)\rightarrow \operatorname{Gal}(K^{\prime \prime }|K)$
of
$s^{\prime \prime }:\operatorname{Gal}(k^{\prime \prime }|k)\rightarrow \operatorname{Gal}(K^{\prime \prime }|K)$
of
![]() $\operatorname{pr}_{K}^{\prime \prime }$
which lifts
$\operatorname{pr}_{K}^{\prime \prime }$
which lifts
![]() $s^{\prime }$
to
$s^{\prime }$
to
![]() $\operatorname{Gal}(k^{\prime \prime }|k)$
.
$\operatorname{Gal}(k^{\prime \prime }|k)$
.
Note that if
![]() $p\neq \text{char}$
, and the
$p\neq \text{char}$
, and the
![]() $p$
th roots of unity
$p$
th roots of unity
![]() $\unicode[STIX]{x1D707}_{p}$
are contained in
$\unicode[STIX]{x1D707}_{p}$
are contained in
![]() $k$
and hence in
$k$
and hence in
![]() $K$
, then by Kummer theory we have
$K$
, then by Kummer theory we have
![]() $K^{\prime }=K[\sqrt[p]{K}]$
and
$K^{\prime }=K[\sqrt[p]{K}]$
and
![]() $K^{\prime \prime }=K^{\prime }[\sqrt[p]{K^{\prime }}]$
and similarly for
$K^{\prime \prime }=K^{\prime }[\sqrt[p]{K^{\prime }}]$
and similarly for
![]() $k$
.
$k$
.
Theorem A. In the above notation, let
![]() $k|\mathbb{Q}_{p}$
be finite with
$k|\mathbb{Q}_{p}$
be finite with
![]() $\unicode[STIX]{x1D707}_{p}\subset k$
. Then the following hold.
$\unicode[STIX]{x1D707}_{p}\subset k$
. Then the following hold.
-
(1) Every
 $k$
-rational point
$k$
-rational point
 $x\in X$
gives rise to a bouquet of conjugacy classes of liftable sections
$x\in X$
gives rise to a bouquet of conjugacy classes of liftable sections
 $s_{x}^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
above
$s_{x}^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
above
 $x$
, which is in bijection with
$x$
, which is in bijection with
 $\text{H}^{1}(\operatorname{Gal}(k^{\prime }|k),T_{x})$
.
$\text{H}^{1}(\operatorname{Gal}(k^{\prime }|k),T_{x})$
. -
(2) Let
 $p>2$
and
$p>2$
and
 $s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
be a liftable section. Then there exists a unique
$s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
be a liftable section. Then there exists a unique
 $k$
-rational point
$k$
-rational point
 $x\in X$
such that
$x\in X$
such that
 $s^{\prime }$
equals one of the sections
$s^{\prime }$
equals one of the sections
 $s_{x}^{\prime }$
as defined above.
$s_{x}^{\prime }$
as defined above.
Actually one can reformulate the question addressed by Theorem A in terms of
![]() $p$
-adic valuations, and get the following stronger result; see § 2(C) for notation, definitions, and a few facts on (formally)
$p$
-adic valuations, and get the following stronger result; see § 2(C) for notation, definitions, and a few facts on (formally)
![]() $p$
-adic valuations
$p$
-adic valuations
![]() $v$
, e.g., the
$v$
, e.g., the
![]() $p$
-adic rank
$p$
-adic rank
![]() $d_{v}$
of
$d_{v}$
of
![]() $v$
and
$v$
and
![]() $p$
-adically closed fields, and Ax and Kochen [Reference Ax and KochenAK66] and Prestel and Roquette [Reference Prestel and RoquettePR85], respectively, for proofs.
$p$
-adically closed fields, and Ax and Kochen [Reference Ax and KochenAK66] and Prestel and Roquette [Reference Prestel and RoquettePR85], respectively, for proofs.
Theorem B. Let
![]() $k$
be a
$k$
be a
![]() $p$
-adically closed field with
$p$
-adically closed field with
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $v$
of
$v$
of
![]() $p$
-adic rank
$p$
-adic rank
![]() $d_{v}$
, and suppose that
$d_{v}$
, and suppose that
![]() $\unicode[STIX]{x1D707}_{p}\subset k$
. Let
$\unicode[STIX]{x1D707}_{p}\subset k$
. Let
![]() $K|k$
be an arbitrary field extension. Then the following hold.
$K|k$
be an arbitrary field extension. Then the following hold.
-
(1) Let
 $w$
be a
$w$
be a
 $p$
-adic valuation of
$p$
-adic valuation of
 $K$
of
$K$
of
 $p$
-adic rank
$p$
-adic rank
 $d_{w}=d_{v}$
. Then
$d_{w}=d_{v}$
. Then
 $w$
prolongs
$w$
prolongs
 $v$
to
$v$
to
 $K$
, and gives rise to a bouquet of conjugacy classes of liftable sections
$K$
, and gives rise to a bouquet of conjugacy classes of liftable sections
 $s_{w}^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
above
$s_{w}^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
above
 $w$
.
$w$
. -
(2) Let
 $p>2$
and
$p>2$
and
 $s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
be a liftable section. Then there exists a unique
$s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
be a liftable section. Then there exists a unique
 $p$
-adic valuation
$p$
-adic valuation
 $w$
of
$w$
of
 $K$
of
$K$
of
 $p$
-adic rank
$p$
-adic rank
 $d_{w}=d_{v}$
such that
$d_{w}=d_{v}$
such that
 $s^{\prime }=s_{w}^{\prime }$
for some
$s^{\prime }=s_{w}^{\prime }$
for some
 $s_{w}^{\prime }$
as above.
$s_{w}^{\prime }$
as above.
Remark/Definition. As mentioned in Pop [Reference PopPop10], the condition
![]() $\unicode[STIX]{x1D707}_{p}\subset k$
is a necessary condition in the above theorems. Nevertheless, as mentioned in [Reference PopPop10], if
$\unicode[STIX]{x1D707}_{p}\subset k$
is a necessary condition in the above theorems. Nevertheless, as mentioned in [Reference PopPop10], if
![]() $\unicode[STIX]{x1D707}_{p}$
is not contained in the base field, assertions similar to Theorems A and B above hold in the following form: let
$\unicode[STIX]{x1D707}_{p}$
is not contained in the base field, assertions similar to Theorems A and B above hold in the following form: let
![]() $l|\mathbb{Q}_{p}$
be some finite extension and
$l|\mathbb{Q}_{p}$
be some finite extension and
![]() $Y\rightarrow l$
a complete geometrically integral smooth variety with function field
$Y\rightarrow l$
a complete geometrically integral smooth variety with function field
![]() $L=\unicode[STIX]{x1D705}(Y)$
. Let
$L=\unicode[STIX]{x1D705}(Y)$
. Let
![]() $k|l$
be a finite Galois extension with
$k|l$
be a finite Galois extension with
![]() $\unicode[STIX]{x1D707}_{p}\subset k$
. Setting
$\unicode[STIX]{x1D707}_{p}\subset k$
. Setting
![]() $K:=Lk$
, consider the field extensions
$K:=Lk$
, consider the field extensions
![]() $K^{\prime }|K{\hookrightarrow}K^{\prime \prime }|K$
and
$K^{\prime }|K{\hookrightarrow}K^{\prime \prime }|K$
and
![]() $k^{\prime }|k{\hookrightarrow}k^{\prime \prime }|k$
as above. Then
$k^{\prime }|k{\hookrightarrow}k^{\prime \prime }|k$
as above. Then
![]() $k^{\prime }=K^{\prime }\cap \overline{l}$
and
$k^{\prime }=K^{\prime }\cap \overline{l}$
and
![]() $k^{\prime \prime }=K^{\prime \prime }\cap \overline{l}$
, and
$k^{\prime \prime }=K^{\prime \prime }\cap \overline{l}$
, and
![]() $K^{\prime }|L$
and
$K^{\prime }|L$
and
![]() $K^{\prime \prime }|L$
, as well as
$K^{\prime \prime }|L$
, as well as
![]() $k^{\prime }|l$
and
$k^{\prime }|l$
and
![]() $k^{\prime \prime }|l$
, are Galois extensions too, and one gets surjective canonical projections
$k^{\prime \prime }|l$
, are Galois extensions too, and one gets surjective canonical projections
In these notations and context we will say that a section
![]() $s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
of
$s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
of
![]() $\operatorname{pr}_{L}^{\prime }$
is liftable if there exists a section
$\operatorname{pr}_{L}^{\prime }$
is liftable if there exists a section
![]() $s_{L}^{\prime \prime }:\operatorname{Gal}(k^{\prime \prime }|l)\rightarrow \operatorname{Gal}(K^{\prime \prime }|L)$
of
$s_{L}^{\prime \prime }:\operatorname{Gal}(k^{\prime \prime }|l)\rightarrow \operatorname{Gal}(K^{\prime \prime }|L)$
of
![]() $\operatorname{pr}_{L}^{\prime \prime }$
which lifts
$\operatorname{pr}_{L}^{\prime \prime }$
which lifts
![]() $s_{L}^{\prime }$
.
$s_{L}^{\prime }$
.
This being said, one has the following extensions of Theorems A and B.
Theorem A0. In the above notation and hypothesis, the following hold.
-
(1) Every
 $l$
-rational point
$l$
-rational point
 $y\in Y$
gives rise to a bouquet of conjugacy classes of liftable sections
$y\in Y$
gives rise to a bouquet of conjugacy classes of liftable sections
 $s_{y}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
above
$s_{y}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
above
 $y$
, which is in bijection with
$y$
, which is in bijection with
 $\text{H}^{1}(\operatorname{Gal}(k^{\prime }|l),T_{y})$
.
$\text{H}^{1}(\operatorname{Gal}(k^{\prime }|l),T_{y})$
. -
(2) Let
 $p>2$
and
$p>2$
and
 $s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
be a liftable section. Then there exists a unique
$s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
be a liftable section. Then there exists a unique
 $l$
-rational point
$l$
-rational point
 $y\in Y$
such that
$y\in Y$
such that
 $s_{L}^{\prime }$
equals one of the sections
$s_{L}^{\prime }$
equals one of the sections
 $s_{y}^{\prime }$
as defined above.
$s_{y}^{\prime }$
as defined above.
Theorem B0. Let
![]() $l$
be a
$l$
be a
![]() $p$
-adically closed field with
$p$
-adically closed field with
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $v$
and let
$v$
and let
![]() $L|l$
be an arbitrary field extension. Then in the above notation the following hold.
$L|l$
be an arbitrary field extension. Then in the above notation the following hold.
-
(1) Let
 $w$
be a
$w$
be a
 $p$
-adic valuation of
$p$
-adic valuation of
 $L$
with
$L$
with
 $d_{w}=d_{v}$
. Then
$d_{w}=d_{v}$
. Then
 $w$
prolongs
$w$
prolongs
 $v$
to
$v$
to
 $L$
, and gives rise to a bouquet of conjugacy classes of liftable sections
$L$
, and gives rise to a bouquet of conjugacy classes of liftable sections
 $s_{w}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
above
$s_{w}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
above
 $w$
.
$w$
. -
(2) Let
 $p>2$
and
$p>2$
and
 $s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
be a liftable section. Then there exists a unique
$s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
be a liftable section. Then there exists a unique
 $p$
-adic valuation
$p$
-adic valuation
 $w$
of
$w$
of
 $L$
such that
$L$
such that
 $d_{w}=d_{v}$
, and
$d_{w}=d_{v}$
, and
 $s_{L}^{\prime }$
equals one of the sections
$s_{L}^{\prime }$
equals one of the sections
 $s_{w}^{\prime }$
as above.
$s_{w}^{\prime }$
as above.
Remark.
As mentioned in Pop [Reference PopPop10], the
![]() $\mathbb{Z}/p$
metabelian form of the birational
$\mathbb{Z}/p$
metabelian form of the birational
![]() $p$
-adic SC for curves implies the corresponding full Galois SC, which was proved in Koenigsmann [Reference KoenigsmannKoe05]. The same holds correspondingly for higher dimensional varieties, provided
$p$
-adic SC for curves implies the corresponding full Galois SC, which was proved in Koenigsmann [Reference KoenigsmannKoe05]. The same holds correspondingly for higher dimensional varieties, provided
![]() $p>2$
, thus implying Stix’s [Reference StixSti13] result in this case. Since the proof of the implication under discussion in the case of general varieties is word-by-word the same as that from [Reference PopPop10], we will not reproduce it here.
$p>2$
, thus implying Stix’s [Reference StixSti13] result in this case. Since the proof of the implication under discussion in the case of general varieties is word-by-word the same as that from [Reference PopPop10], we will not reproduce it here.
An interesting application of the results and techniques developed here is the following fact concerning the
![]() $p$
-adic section conjecture for varieties: let
$p$
-adic section conjecture for varieties: let
![]() $k|\mathbb{Q}_{p}$
be a finite extension and
$k|\mathbb{Q}_{p}$
be a finite extension and
![]() $X$
a complete smooth
$X$
a complete smooth
![]() $k$
-variety. Then there exists a finite effectively computable family of finite geometrically
$k$
-variety. Then there exists a finite effectively computable family of finite geometrically
![]() $\mathbb{Z}/p$
elementary abelian (ramified) covers
$\mathbb{Z}/p$
elementary abelian (ramified) covers
![]() $\unicode[STIX]{x1D711}_{i}:X_{i}\rightarrow X$
,
$\unicode[STIX]{x1D711}_{i}:X_{i}\rightarrow X$
,
![]() $i\in I$
, satisfying:
$i\in I$
, satisfying:
-
(i)
 $\bigcup _{i}\unicode[STIX]{x1D711}_{i}(X_{i}(k))=X(k)$
, i.e., every
$\bigcup _{i}\unicode[STIX]{x1D711}_{i}(X_{i}(k))=X(k)$
, i.e., every
 $x\in X(k)$
‘survives’ in at least one of the covers
$x\in X(k)$
‘survives’ in at least one of the covers
 $X_{i}\rightarrow X$
;
$X_{i}\rightarrow X$
; -
(ii) a section
 $s:G_{k}\rightarrow \unicode[STIX]{x1D70B}_{1}(X,\ast )$
can be lifted to a section
$s:G_{k}\rightarrow \unicode[STIX]{x1D70B}_{1}(X,\ast )$
can be lifted to a section
 $s_{i}:G_{k}\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{i},\ast )$
for some
$s_{i}:G_{k}\rightarrow \unicode[STIX]{x1D70B}_{1}(X_{i},\ast )$
for some
 $i\in I$
if and only if
$i\in I$
if and only if
 $s$
arises from a
$s$
arises from a
 $k$
-rational point
$k$
-rational point
 $x\in X(k)$
in the way described above.
$x\in X(k)$
in the way described above.
The main technical tools for the proof of the above theorems are:
-
∙ the techniques developed in Pop [Reference PopPop10] (which refine facts/methods initiated in [Reference PopPop88]);
-
∙ the theory of rigid elements, as developed by several people: Ware [Reference WareWar81], Arason et al. [Reference Arason, Elman and JacobAEJ87], Koenigsmann [Reference KoenigsmannKoe95], Efrat [Reference EfratEfr99], etc. See Topaz [Reference TopazTop15] as the definitive reference.
As a final remark, we notice that the condition
![]() $p>2$
in the results above originates from the weaker results about recovering valuations from rigid elements in the case
$p>2$
in the results above originates from the weaker results about recovering valuations from rigid elements in the case
![]() $p=2$
. This technical condition might be removable, but some new ideas/techniques might be necessary to do so; see the comment at the beginning of the proof of assertion (2) of Theorem B in § 3.
$p=2$
. This technical condition might be removable, but some new ideas/techniques might be necessary to do so; see the comment at the beginning of the proof of assertion (2) of Theorem B in § 3.
2 Reviewing a few known facts
For the reader’s sake, in this section we review a few known facts about valuation theory, decomposition theory, and (formally)
![]() $p$
-adic fields, but do not reproduce proofs.
$p$
-adic fields, but do not reproduce proofs.
(A) Generalities about valuations and their Hilbert decomposition theory
For an arbitrary field
![]() $K$
and an arbitrary valuation
$K$
and an arbitrary valuation
![]() $v$
of
$v$
of
![]() $K$
, we denote usually by
$K$
, we denote usually by
![]() ${\mathcal{O}}_{v},\mathfrak{m}_{v}$
the valuation ring/ideal of
${\mathcal{O}}_{v},\mathfrak{m}_{v}$
the valuation ring/ideal of
![]() $v$
, by
$v$
, by
![]() $vK=K^{\times }/{\mathcal{O}}^{\times }$
the value group of
$vK=K^{\times }/{\mathcal{O}}^{\times }$
the value group of
![]() $v$
, and by
$v$
, and by
![]() $Kv=:{\mathcal{O}}_{v}/\mathfrak{m}_{v}:=\unicode[STIX]{x1D705}(v)$
the residue field of
$Kv=:{\mathcal{O}}_{v}/\mathfrak{m}_{v}:=\unicode[STIX]{x1D705}(v)$
the residue field of
![]() $v$
. Further,
$v$
. Further,
![]() $U_{v}^{1}:=1+\mathfrak{m}_{v}\subset U_{v}$
denote the groups of principal
$U_{v}^{1}:=1+\mathfrak{m}_{v}\subset U_{v}$
denote the groups of principal
![]() $v$
-units and
$v$
-units and
![]() $v$
-units, respectively. One has the following canonical exact sequences:
$v$
-units, respectively. One has the following canonical exact sequences:
The set of ideals of
![]() ${\mathcal{O}}_{v}$
is totally ordered with respect to inclusion. The subrings
${\mathcal{O}}_{v}$
is totally ordered with respect to inclusion. The subrings
![]() ${\mathcal{O}}_{1}\subseteq K$
with
${\mathcal{O}}_{1}\subseteq K$
with
![]() ${\mathcal{O}}_{v}\subseteq {\mathcal{O}}_{1}$
are precisely the localizations
${\mathcal{O}}_{v}\subseteq {\mathcal{O}}_{1}$
are precisely the localizations
![]() ${\mathcal{O}}_{1}:=({\mathcal{O}}_{v})_{\mathfrak{m}_{1}}$
with
${\mathcal{O}}_{1}:=({\mathcal{O}}_{v})_{\mathfrak{m}_{1}}$
with
![]() $\mathfrak{m}_{1}\in \operatorname{Spec}({\mathcal{O}}_{v})$
and, moreover,
$\mathfrak{m}_{1}\in \operatorname{Spec}({\mathcal{O}}_{v})$
and, moreover,
![]() $\mathfrak{m}_{1}\subset {\mathcal{O}}_{v}$
, and
$\mathfrak{m}_{1}\subset {\mathcal{O}}_{v}$
, and
![]() $({\mathcal{O}}_{v})_{\mathfrak{m}_{1}}$
is a valuation ring with valuation ideal
$({\mathcal{O}}_{v})_{\mathfrak{m}_{1}}$
is a valuation ring with valuation ideal
![]() $\mathfrak{m}_{1}$
. Further, if
$\mathfrak{m}_{1}$
. Further, if
![]() $v_{1}$
is the corresponding valuation of
$v_{1}$
is the corresponding valuation of
![]() $K$
, then
$K$
, then
![]() ${\mathcal{O}}_{0}:={\mathcal{O}}_{v}/\mathfrak{m}_{1}$
is a valuation ring of
${\mathcal{O}}_{0}:={\mathcal{O}}_{v}/\mathfrak{m}_{1}$
is a valuation ring of
![]() $Kv_{1}$
with valuation ideal
$Kv_{1}$
with valuation ideal
![]() $\mathfrak{m}_{0}:=\mathfrak{m}_{v}/\mathfrak{m}_{1}$
, say of a valuation
$\mathfrak{m}_{0}:=\mathfrak{m}_{v}/\mathfrak{m}_{1}$
, say of a valuation
![]() $v_{0}$
of
$v_{0}$
of
![]() $Kv_{1}$
. We say that
$Kv_{1}$
. We say that
![]() $v_{1}$
is a coarsening of
$v_{1}$
is a coarsening of
![]() $v$
, and denote
$v$
, and denote
![]() $v_{1}\leqslant v$
and
$v_{1}\leqslant v$
and
![]() $v_{0}:=v/v_{1}$
.
$v_{0}:=v/v_{1}$
.
Conversely, if
![]() $v_{1}$
is a valuation of
$v_{1}$
is a valuation of
![]() $K$
and
$K$
and
![]() $v_{0}$
is a valuation on the residue field
$v_{0}$
is a valuation on the residue field
![]() $Kv_{1}$
, then the preimage of the valuation ring
$Kv_{1}$
, then the preimage of the valuation ring
![]() ${\mathcal{O}}_{v_{0}}\subseteq Kv_{1}$
under
${\mathcal{O}}_{v_{0}}\subseteq Kv_{1}$
under
![]() ${\mathcal{O}}_{v_{1}}\rightarrow Kv_{1}$
is a valuation ring
${\mathcal{O}}_{v_{1}}\rightarrow Kv_{1}$
is a valuation ring
![]() ${\mathcal{O}}\subseteq {\mathcal{O}}_{v_{1}}$
having as valuation ideal the preimage
${\mathcal{O}}\subseteq {\mathcal{O}}_{v_{1}}$
having as valuation ideal the preimage
![]() $\mathfrak{m}\subset {\mathcal{O}}$
of
$\mathfrak{m}\subset {\mathcal{O}}$
of
![]() $\mathfrak{m}_{v_{0}}$
. Hence, if
$\mathfrak{m}_{v_{0}}$
. Hence, if
![]() $v$
is the valuation defined by
$v$
is the valuation defined by
![]() ${\mathcal{O}}$
on
${\mathcal{O}}$
on
![]() $K$
, then
$K$
, then
![]() $Kv=(Kv_{1})v_{0}$
and one has a canonical exact sequence of totally ordered groups:
$Kv=(Kv_{1})v_{0}$
and one has a canonical exact sequence of totally ordered groups:
The relation between coarsening and decomposition theory is as follows. Let
![]() $\tilde{K}|K$
be a Galois extension and
$\tilde{K}|K$
be a Galois extension and
![]() $\tilde{v}|v$
be a prolongation of
$\tilde{v}|v$
be a prolongation of
![]() $v$
to
$v$
to
![]() $\tilde{K}$
. Then the coarsenings
$\tilde{K}$
. Then the coarsenings
![]() $\tilde{v}_{1}$
of
$\tilde{v}_{1}$
of
![]() $\tilde{v}$
are in a canonical bijection with the coarsenings
$\tilde{v}$
are in a canonical bijection with the coarsenings
![]() $v_{1}$
of
$v_{1}$
of
![]() $v$
via
$v$
via
![]() ${\mathcal{O}}_{\tilde{v}_{1}}\mapsto {\mathcal{O}}_{v_{1}}:={\mathcal{O}}_{\tilde{v}_{1}}\cap K$
; thus,
${\mathcal{O}}_{\tilde{v}_{1}}\mapsto {\mathcal{O}}_{v_{1}}:={\mathcal{O}}_{\tilde{v}_{1}}\cap K$
; thus,
![]() ${\mathcal{O}}_{\tilde{v}_{1}}={\mathcal{O}}_{\tilde{v}}\cdot {\mathcal{O}}_{v_{1}}$
. Let
${\mathcal{O}}_{\tilde{v}_{1}}={\mathcal{O}}_{\tilde{v}}\cdot {\mathcal{O}}_{v_{1}}$
. Let
![]() $\tilde{v}_{1}|v_{1}$
be given coarsenings of
$\tilde{v}_{1}|v_{1}$
be given coarsenings of
![]() $\tilde{v}|v$
and
$\tilde{v}|v$
and
![]() $\tilde{K}\tilde{v}_{1}|Kv_{1}$
be the corresponding residue field extension. Then
$\tilde{K}\tilde{v}_{1}|Kv_{1}$
be the corresponding residue field extension. Then
![]() $\tilde{v}_{0}:=\tilde{v}/\tilde{v}_{1}$
is canonically a prolongation of
$\tilde{v}_{0}:=\tilde{v}/\tilde{v}_{1}$
is canonically a prolongation of
![]() $v_{0}:=v/v_{1}$
.
$v_{0}:=v/v_{1}$
.
Fact 1. Let
![]() $T_{\tilde{v}}\subseteq Z_{\tilde{v}}$
and
$T_{\tilde{v}}\subseteq Z_{\tilde{v}}$
and
![]() $T_{\tilde{v}_{1}}\subseteq Z_{\tilde{v}_{1}}$
be the corresponding inertia/decomposition groups, and set
$T_{\tilde{v}_{1}}\subseteq Z_{\tilde{v}_{1}}$
be the corresponding inertia/decomposition groups, and set
![]() $G_{\tilde{v}_{1}}=\operatorname{Aut}(\tilde{K}\tilde{v}_{1}|Kv_{1})$
. Then one has a canonical exact sequence
$G_{\tilde{v}_{1}}=\operatorname{Aut}(\tilde{K}\tilde{v}_{1}|Kv_{1})$
. Then one has a canonical exact sequence
![]() $1\rightarrow T_{\tilde{v}_{1}}\rightarrow Z_{\tilde{v}_{1}}\rightarrow G_{\tilde{v}_{1}}\rightarrow 1$
, and the inertia/decomposition groups satisfy:
$1\rightarrow T_{\tilde{v}_{1}}\rightarrow Z_{\tilde{v}_{1}}\rightarrow G_{\tilde{v}_{1}}\rightarrow 1$
, and the inertia/decomposition groups satisfy:
-
(a)
 $Z_{\tilde{v}}\subseteq Z_{\tilde{v}_{1}}$
and
$Z_{\tilde{v}}\subseteq Z_{\tilde{v}_{1}}$
and
 $T_{\tilde{v}}\supseteq T_{\tilde{v}_{1}}$
. Further,
$T_{\tilde{v}}\supseteq T_{\tilde{v}_{1}}$
. Further,
 $T_{\tilde{v}_{1}}$
is a normal subgroup of
$T_{\tilde{v}_{1}}$
is a normal subgroup of
 $Z_{\tilde{v}}$
;
$Z_{\tilde{v}}$
; -
(b) via
 $1\rightarrow T_{\tilde{v}_{1}}\rightarrow Z_{\tilde{v}_{1}}\rightarrow G_{\tilde{v}_{1}}=Z_{\tilde{v}_{1}}/T_{\tilde{v}_{1}}\rightarrow 1$
, one has that
$1\rightarrow T_{\tilde{v}_{1}}\rightarrow Z_{\tilde{v}_{1}}\rightarrow G_{\tilde{v}_{1}}=Z_{\tilde{v}_{1}}/T_{\tilde{v}_{1}}\rightarrow 1$
, one has that
 $T_{\tilde{v}_{0}}=T_{\tilde{v}}/T_{\tilde{v}_{1}}$
and
$T_{\tilde{v}_{0}}=T_{\tilde{v}}/T_{\tilde{v}_{1}}$
and
 $Z_{\tilde{v}_{0}}=Z_{\tilde{v}}/T_{\tilde{v}_{1}}$
.
$Z_{\tilde{v}_{0}}=Z_{\tilde{v}}/T_{\tilde{v}_{1}}$
.
(B) Hilbert decomposition in elementary abelian extensions
Let
![]() $K$
be a field of characteristic prime to
$K$
be a field of characteristic prime to
![]() $p$
containing
$p$
containing
![]() $\unicode[STIX]{x1D707}_{n}$
, where
$\unicode[STIX]{x1D707}_{n}$
, where
![]() $n=p^{e}$
is a power of the prime number
$n=p^{e}$
is a power of the prime number
![]() $p$
, and let
$p$
, and let
![]() $\tilde{K}=K[\sqrt[n]{K}]$
be the maximal
$\tilde{K}=K[\sqrt[n]{K}]$
be the maximal
![]() $\mathbb{Z}/n$
elementary abelian extension of
$\mathbb{Z}/n$
elementary abelian extension of
![]() $K$
. Let
$K$
. Let
![]() $v$
be a valuation of
$v$
be a valuation of
![]() $K$
,
$K$
,
![]() $\tilde{v}$
be some prolongation of
$\tilde{v}$
be some prolongation of
![]() $v$
to
$v$
to
![]() $\tilde{K}$
, and
$\tilde{K}$
, and
![]() $V_{\tilde{v}}\subseteq T_{\tilde{v}}\subseteq Z_{\tilde{v}}$
be the ramification, the inertia, and the decomposition, groups of
$V_{\tilde{v}}\subseteq T_{\tilde{v}}\subseteq Z_{\tilde{v}}$
be the ramification, the inertia, and the decomposition, groups of
![]() $\tilde{v}|v$
, respectively. We remark that because
$\tilde{v}|v$
, respectively. We remark that because
![]() $\operatorname{Gal}(\tilde{K}|K)$
is commutative, the groups
$\operatorname{Gal}(\tilde{K}|K)$
is commutative, the groups
![]() $V_{\tilde{v}}$
,
$V_{\tilde{v}}$
,
![]() $T_{\tilde{v}}$
, and
$T_{\tilde{v}}$
, and
![]() $Z_{\tilde{v}}$
depend on
$Z_{\tilde{v}}$
depend on
![]() $v$
only. Therefore, we will simply denote them by
$v$
only. Therefore, we will simply denote them by
![]() $V_{v}$
,
$V_{v}$
,
![]() $T_{v}$
, and
$T_{v}$
, and
![]() $Z_{v}$
. Finally, we denote by
$Z_{v}$
. Finally, we denote by
![]() $K^{Z}\subseteq K^{T}\subseteq K^{V}$
the corresponding fixed fields in
$K^{Z}\subseteq K^{T}\subseteq K^{V}$
the corresponding fixed fields in
![]() $\tilde{K}$
. One has the following, see e.g. Pop [Reference PopPop10, §2] (where the case
$\tilde{K}$
. One has the following, see e.g. Pop [Reference PopPop10, §2] (where the case
![]() $n=p$
is dealt with; but the proof is similar for general
$n=p$
is dealt with; but the proof is similar for general
![]() $n=p^{e}$
and we will not reproduce the details here).
$n=p^{e}$
and we will not reproduce the details here).
Fact 2. In the above notation, the following hold.
-
(1) Let
 $U^{v}:=1+p^{2e}\mathfrak{m}_{v}$
. Then
$U^{v}:=1+p^{2e}\mathfrak{m}_{v}$
. Then
 $\sqrt[n]{U^{v}}\subset K^{Z}$
, and
$\sqrt[n]{U^{v}}\subset K^{Z}$
, and
 $K^{Z}=K[\sqrt[n]{1+\mathfrak{m}_{v}}]$
, provided
$K^{Z}=K[\sqrt[n]{1+\mathfrak{m}_{v}}]$
, provided
 $\text{char}(Kv)\neq p$
. In particular, if
$\text{char}(Kv)\neq p$
. In particular, if
 $w_{1}$
and
$w_{1}$
and
 $w_{2}$
are independent valuations of
$w_{2}$
are independent valuations of
 $K$
, then
$K$
, then
 $Z_{w_{1}}\cap Z_{w_{2}}=1$
.
$Z_{w_{1}}\cap Z_{w_{2}}=1$
. -
(2) If
 $p\neq \operatorname{char}(Kv)$
, then
$p\neq \operatorname{char}(Kv)$
, then
 $V_{v}=1$
and
$V_{v}=1$
and
 $\tilde{K}\tilde{v}=\widetilde{Kv}$
and hence
$\tilde{K}\tilde{v}=\widetilde{Kv}$
and hence
 $G_{v}:=Z_{v}/T_{v}=\operatorname{Gal}(\widetilde{Kv}|Kv)$
in this case. And, if
$G_{v}:=Z_{v}/T_{v}=\operatorname{Gal}(\widetilde{Kv}|Kv)$
in this case. And, if
 $p=\operatorname{char}(Kv)$
, then
$p=\operatorname{char}(Kv)$
, then
 $V_{v}=T_{v}$
, and the residue field
$V_{v}=T_{v}$
, and the residue field
 $\tilde{K}\tilde{v}$
contains
$\tilde{K}\tilde{v}$
contains
 $(Kv)^{1/n}$
and a maximal
$(Kv)^{1/n}$
and a maximal
 $\mathbb{Z}/n$
elementary abelian extension of
$\mathbb{Z}/n$
elementary abelian extension of
 $Kv$
.
$Kv$
. -
(3) Let
 $L:=K_{v}^{\text{h}}$
be the Henselization of
$L:=K_{v}^{\text{h}}$
be the Henselization of
 $K$
with respect to
$K$
with respect to
 $v$
. Then
$v$
. Then
 $\tilde{L}=L\tilde{K}$
is a maximal
$\tilde{L}=L\tilde{K}$
is a maximal
 $\mathbb{Z}/n$
elementary extension of
$\mathbb{Z}/n$
elementary extension of
 $L$
. Therefore, we have
$L$
. Therefore, we have
 $\operatorname{Gal}(\tilde{L}|L)\cong Z_{\tilde{v}}$
canonically.
$\operatorname{Gal}(\tilde{L}|L)\cong Z_{\tilde{v}}$
canonically.
(C) Formally
![]() $p$
-adic fields and
$p$
-adic fields and
![]() $p$
-adic valuations
$p$
-adic valuations
We recall a few basic facts about
![]() $p$
-adic valuations and (formally)
$p$
-adic valuations and (formally)
![]() $p$
-adically closed fields; see Ax and Kochen [Reference Ax and KochenAK66] and Prestel and Roquette [Reference Prestel and RoquettePR85] for more details.
$p$
-adically closed fields; see Ax and Kochen [Reference Ax and KochenAK66] and Prestel and Roquette [Reference Prestel and RoquettePR85] for more details.
-
(1) A valuation
 $v$
of a field
$v$
of a field
 $k$
is called (formally)
$k$
is called (formally)
 $p$
-adic if its residue field
$p$
-adic if its residue field
 $kv$
is a finite field, say
$kv$
is a finite field, say
 $\mathbb{F}_{q}$
with
$\mathbb{F}_{q}$
with
 $q=p^{f_{v}}$
elements, and the value group
$q=p^{f_{v}}$
elements, and the value group
 $vk$
has a minimal positive element
$vk$
has a minimal positive element
 $1_{v}$
such that
$1_{v}$
such that
 $v(p)=e_{v}\cdot 1_{v}$
for some natural number
$v(p)=e_{v}\cdot 1_{v}$
for some natural number
 $e_{v}>0$
. The number
$e_{v}>0$
. The number
 $d_{v}:=e_{v}f_{v}$
is called the
$d_{v}:=e_{v}f_{v}$
is called the
 $p$
-adic rank (or degree) of the
$p$
-adic rank (or degree) of the
 $p$
-adic valuation
$p$
-adic valuation
 $v$
. Note that a field
$v$
. Note that a field
 $k$
carrying a
$k$
carrying a
 $p$
-adic valuation
$p$
-adic valuation
 $v$
must necessarily have
$v$
must necessarily have
 $\operatorname{char}(k)=0$
, as
$\operatorname{char}(k)=0$
, as
 $v(p)\neq \infty$
, and
$v(p)\neq \infty$
, and
 $\operatorname{char}(kv)=p$
.
$\operatorname{char}(kv)=p$
. -
(2) Let
 $v$
be a
$v$
be a
 $p$
-adic valuation of
$p$
-adic valuation of
 $k$
with valuation ring
$k$
with valuation ring
 ${\mathcal{O}}_{v}$
. Then
${\mathcal{O}}_{v}$
. Then
 ${\mathcal{O}}_{1}:={\mathcal{O}}_{v}[1/p]$
is the valuation ring of the unique maximal proper coarsening
${\mathcal{O}}_{1}:={\mathcal{O}}_{v}[1/p]$
is the valuation ring of the unique maximal proper coarsening
 $v_{1}$
of
$v_{1}$
of
 $v$
, which is called the canonical coarsening of
$v$
, which is called the canonical coarsening of
 $v$
. Note that setting
$v$
. Note that setting
 $k_{0}:=kv_{1}$
, and
$k_{0}:=kv_{1}$
, and
 $v_{0}:=v/v_{1}$
the corresponding valuation on
$v_{0}:=v/v_{1}$
the corresponding valuation on
 $k_{0}$
, we have:
$k_{0}$
, we have:
 $v_{0}$
is a
$v_{0}$
is a
 $p$
-adic valuation of
$p$
-adic valuation of
 $k_{0}$
with
$k_{0}$
with
 $e_{v_{0}}=e_{v}$
and
$e_{v_{0}}=e_{v}$
and
 $f_{v_{0}}=f_{v}$
; hence,
$f_{v_{0}}=f_{v}$
; hence,
 $d_{v_{0}}=d_{v}$
and, moreover,
$d_{v_{0}}=d_{v}$
and, moreover,
 $v_{0}$
is a discrete valuation of
$v_{0}$
is a discrete valuation of
 $k_{0}$
. In particular, the following hold.
$k_{0}$
. In particular, the following hold.-
(a)
 $v$
has rank one if and only if
$v$
has rank one if and only if
 $v_{1}$
is the trivial valuation if and only if
$v_{1}$
is the trivial valuation if and only if
 $v=v_{0}$
.
$v=v_{0}$
. -
(b) Giving a
 $p$
-adic valuation
$p$
-adic valuation
 $v$
of a field
$v$
of a field
 $k$
of
$k$
of
 $p$
-adic rank
$p$
-adic rank
 $d_{v}=e_{v}f_{v}$
is equivalent to giving a place
$d_{v}=e_{v}f_{v}$
is equivalent to giving a place
 $\mathfrak{p}$
of
$\mathfrak{p}$
of
 $k$
with values in a finite extension
$k$
with values in a finite extension
 $\boldsymbol{k}_{0}$
of
$\boldsymbol{k}_{0}$
of
 $\mathbb{Q}_{p}$
such that the residue field
$\mathbb{Q}_{p}$
such that the residue field
 $k_{0}:=k\mathfrak{p}$
of
$k_{0}:=k\mathfrak{p}$
of
 $\mathfrak{p}$
is dense in
$\mathfrak{p}$
is dense in
 $\boldsymbol{k}_{0}$
, and
$\boldsymbol{k}_{0}$
, and
 $\boldsymbol{k}_{0}|\mathbb{Q}_{p}$
has ramification index
$\boldsymbol{k}_{0}|\mathbb{Q}_{p}$
has ramification index
 $e_{v}$
and residual degree
$e_{v}$
and residual degree
 $f_{v}$
.
$f_{v}$
. -
(c) If
 $v_{i}<v$
is a strict coarsening of
$v_{i}<v$
is a strict coarsening of
 $v$
, then
$v$
, then
 $v_{i}\leqslant v_{1}$
, and the quotient valuation
$v_{i}\leqslant v_{1}$
, and the quotient valuation
 $v/v_{i}$
on the residue field
$v/v_{i}$
on the residue field
 $kv_{i}$
is a
$kv_{i}$
is a
 $p$
-adic valuation with
$p$
-adic valuation with
 $e_{v/v_{i}}=e_{v}$
and
$e_{v/v_{i}}=e_{v}$
and
 $f_{v/v_{i}}=f_{v}$
; thus,
$f_{v/v_{i}}=f_{v}$
; thus,
 $d_{v/v_{i}}=d_{v}$
. (Actually,
$d_{v/v_{i}}=d_{v}$
. (Actually,
 $\unicode[STIX]{x1D705}(v_{i}/v_{1})\cong kv_{1}$
and
$\unicode[STIX]{x1D705}(v_{i}/v_{1})\cong kv_{1}$
and
 $\unicode[STIX]{x1D705}(v_{i}/v)\cong kv$
canonically.)
$\unicode[STIX]{x1D705}(v_{i}/v)\cong kv$
canonically.)
-
-
(3) Let
 $v$
be a
$v$
be a
 $p$
-adic valuation of
$p$
-adic valuation of
 $k$
,
$k$
,
 $l|k$
a finite field extension, and denote by
$l|k$
a finite field extension, and denote by
 $w|v$
the prolongations of
$w|v$
the prolongations of
 $v$
to
$v$
to
 $l$
. Then the following hold.
$l$
. Then the following hold.-
(a) All prolongations
 $w|v$
are
$w|v$
are
 $p$
-adic valuations. Further, the fundamental equality holds for the finite extension
$p$
-adic valuations. Further, the fundamental equality holds for the finite extension
 $l|k$
, i.e.,
$l|k$
, i.e.,
 $[l:k]=\sum _{w|v}e(w|v)f(w|v)$
, where
$[l:k]=\sum _{w|v}e(w|v)f(w|v)$
, where
 $e(w|v)$
and
$e(w|v)$
and
 $f(w|v)$
are the ramification index and the residual degree, respectively, of
$f(w|v)$
are the ramification index and the residual degree, respectively, of
 $w|v$
.
$w|v$
. -
(b) For each
 $w|v$
, let
$w|v$
, let
 $w_{1}$
be the canonical coarsening of
$w_{1}$
be the canonical coarsening of
 $w$
, and
$w$
, and
 $w_{0}=w/w_{1}$
be the canonical quotient on the residue field
$w_{0}=w/w_{1}$
be the canonical quotient on the residue field
 $lw_{1}$
. Then by general decomposition theory of valuations one has
$lw_{1}$
. Then by general decomposition theory of valuations one has
 $e(w|v)=e(w_{1}|v_{1})e(w_{0}|v_{0})$
and
$e(w|v)=e(w_{1}|v_{1})e(w_{0}|v_{0})$
and
 $f(w|v)=f(w_{0}|v_{0})$
. Further,
$f(w|v)=f(w_{0}|v_{0})$
. Further,
 $e_{w}=e(w_{0}|v_{0})e_{v}$
and
$e_{w}=e(w_{0}|v_{0})e_{v}$
and
 $f_{w}=f(w|v)f_{v}$
; thus,
$f_{w}=f(w|v)f_{v}$
; thus,
 $d_{w}=e(w_{0}|v_{0})f(w|v)d_{v}$
.
$d_{w}=e(w_{0}|v_{0})f(w|v)d_{v}$
. -
(c) In particular, if
 $l|k$
is Galois, and
$l|k$
is Galois, and
 $w^{Z}$
is the restriction of
$w^{Z}$
is the restriction of
 $w$
to the decomposition field
$w$
to the decomposition field
 $l^{Z}$
of
$l^{Z}$
of
 $w$
, then
$w$
, then
 $e(w|w^{Z})=e(w|v)$
and
$e(w|w^{Z})=e(w|v)$
and
 $f(w|w^{Z})=f(w|v)$
; thus,
$f(w|w^{Z})=f(w|v)$
; thus,
 $w^{Z}$
is a
$w^{Z}$
is a
 $p$
-adic valuation having
$p$
-adic valuation having
 $p$
-adic rank equal to the one of
$p$
-adic rank equal to the one of
 $v$
. Further, the same is true for infinite Galois extensions
$v$
. Further, the same is true for infinite Galois extensions
 $l|k$
.
$l|k$
.
-
-
(4) A field
 $k$
is called (formally)
$k$
is called (formally)
 $p$
-adically closed if
$p$
-adically closed if
 $k$
carries a
$k$
carries a
 $p$
-adic valuation
$p$
-adic valuation
 $v$
such that for every finite extension
$v$
such that for every finite extension
 $\tilde{k}|k$
, one has: if
$\tilde{k}|k$
, one has: if
 $v$
has a prolongation
$v$
has a prolongation
 $\tilde{v}$
to
$\tilde{v}$
to
 $\tilde{k}$
with
$\tilde{k}$
with
 $d_{\tilde{v}}=d_{v}$
, then
$d_{\tilde{v}}=d_{v}$
, then
 $\tilde{k}=k$
. One has the following characterization of the
$\tilde{k}=k$
. One has the following characterization of the
 $p$
-adically closed fields: for a field
$p$
-adically closed fields: for a field
 $k$
endowed with a
$k$
endowed with a
 $p$
-adic valuation
$p$
-adic valuation
 $v$
, and its canonical coarsening
$v$
, and its canonical coarsening
 $v_{1}$
, the following are equivalent.
$v_{1}$
, the following are equivalent.-
(i)
 $k$
is
$k$
is
 $p$
-adically closed with respect to
$p$
-adically closed with respect to
 $v$
.
$v$
. -
(ii)
 $v$
is Henselian and
$v$
is Henselian and
 $v_{1}k$
is divisible (maybe trivial).
$v_{1}k$
is divisible (maybe trivial). -
(iii)
 $v_{1}$
is Henselian,
$v_{1}$
is Henselian,
 $v_{1}k$
is divisible (maybe trivial), and the residue field
$v_{1}k$
is divisible (maybe trivial), and the residue field
 $k_{0}:=kv_{1}$
is relatively algebraically closed in its
$k_{0}:=kv_{1}$
is relatively algebraically closed in its
 $v_{0}=v/v_{1}$
completion
$v_{0}=v/v_{1}$
completion
 $\boldsymbol{k}_{0}$
(itself a finite extension of
$\boldsymbol{k}_{0}$
(itself a finite extension of
 $\mathbb{Q}_{p}$
).
$\mathbb{Q}_{p}$
).
Further, the
 $p$
-adic valuation of a
$p$
-adic valuation of a
 $p$
-adically closed field is definable and unique.
$p$
-adically closed field is definable and unique. -
-
(5) Finally, for every field
 $k$
endowed with a
$k$
endowed with a
 $p$
-adic valuation
$p$
-adic valuation
 $v$
, there exist
$v$
, there exist
 $p$
-adic closures
$p$
-adic closures
 $\widehat{k},\widehat{v}$
such that
$\widehat{k},\widehat{v}$
such that
 $d_{\widehat{v}}=d_{v}$
. Moreover, the space of the
$d_{\widehat{v}}=d_{v}$
. Moreover, the space of the
 $k$
-isomorphy classes of
$k$
-isomorphy classes of
 $p$
-adic closures of
$p$
-adic closures of
 $k,v$
has a concrete description as follows: let
$k,v$
has a concrete description as follows: let
 $v_{1}$
be the canonical coarsening of
$v_{1}$
be the canonical coarsening of
 $v$
, and
$v$
, and
 $\boldsymbol{k}_{0}|\mathbb{Q}_{p}$
the completion of the residue field of
$\boldsymbol{k}_{0}|\mathbb{Q}_{p}$
the completion of the residue field of
 $k_{0}=kv_{1}$
with respect to the discrete valuation
$k_{0}=kv_{1}$
with respect to the discrete valuation
 $v_{0}=v/v_{1}$
. Recalling the canonical exact sequence
$v_{0}=v/v_{1}$
. Recalling the canonical exact sequence
 $1\rightarrow I_{v_{1}}\xrightarrow[{}]{}D_{v}\xrightarrow[{}]{\text{pr}}G_{\boldsymbol{k}_{0}}\rightarrow 1$
, one has that the space of the isomorphy classes of
$1\rightarrow I_{v_{1}}\xrightarrow[{}]{}D_{v}\xrightarrow[{}]{\text{pr}}G_{\boldsymbol{k}_{0}}\rightarrow 1$
, one has that the space of the isomorphy classes of
 $p$
-adic closures of
$p$
-adic closures of
 $k,v$
is in bijection with the space of conjugacy classes of sections of
$k,v$
is in bijection with the space of conjugacy classes of sections of
 $\text{pr}$
and thus with
$\text{pr}$
and thus with
 $\text{H}_{\text{cont}}^{1}(G_{\boldsymbol{k}_{0}},I_{v_{1}})$
.
$\text{H}_{\text{cont}}^{1}(G_{\boldsymbol{k}_{0}},I_{v_{1}})$
. -
(6) In the above notation, the following hold.
-
(a) Let
 $k,v$
be a
$k,v$
be a
 $p$
-adically closed field. Then
$p$
-adically closed field. Then
 $k_{0}=kv_{1}$
is
$k_{0}=kv_{1}$
is
 $p$
-adically closed (with respect to
$p$
-adically closed (with respect to
 $v_{0}$
), and
$v_{0}$
), and
 $k^{\text{abs}}$
is actually the relative algebraic closure of
$k^{\text{abs}}$
is actually the relative algebraic closure of
 $\mathbb{Q}$
in
$\mathbb{Q}$
in
 $k_{0}$
. Further,
$k_{0}$
. Further,
 $\overline{k}=k\overline{\mathbb{Q}}$
.
$\overline{k}=k\overline{\mathbb{Q}}$
. -
(b) The elementary equivalence class of a
 $p$
-adically closed field
$p$
-adically closed field
 $k$
is determined by both the absolute subfield
$k$
is determined by both the absolute subfield
 $k^{\text{abs}}:=k\cap \overline{\mathbb{Q}}=k_{0}\cap \overline{\mathbb{Q}}$
of
$k^{\text{abs}}:=k\cap \overline{\mathbb{Q}}=k_{0}\cap \overline{\mathbb{Q}}$
of
 $k$
and the completion
$k$
and the completion
 $\boldsymbol{k}_{0}$
of
$\boldsymbol{k}_{0}$
of
 $k_{0}=kv_{1}$
with respect to
$k_{0}=kv_{1}$
with respect to
 $v_{0}$
(which equals the completion of
$v_{0}$
(which equals the completion of
 $k^{\text{abs}}$
with respect to
$k^{\text{abs}}$
with respect to
 $v_{0}$
as well).
$v_{0}$
as well). -
(c) If
 $N$
is
$N$
is
 $p$
-adically closed with respect to the
$p$
-adically closed with respect to the
 $p$
-adic valuation
$p$
-adic valuation
 $w$
, and
$w$
, and
 $k\subseteq N$
is a subfield which is relatively closed in
$k\subseteq N$
is a subfield which is relatively closed in
 $N$
, then
$N$
, then
 $k$
is
$k$
is
 $p$
-adically closed with respect to
$p$
-adically closed with respect to
 $v:=w|_{k}$
,
$v:=w|_{k}$
,
 $v$
and
$v$
and
 $w$
have equal
$w$
have equal
 $p$
-adic ranks, and
$p$
-adic ranks, and
 $N$
and
$N$
and
 $k$
are elementary equivalent.
$k$
are elementary equivalent. -
(d) If
 $N|k$
is an extension of
$N|k$
is an extension of
 $p$
-adically closed fields of the same rank, the following hold.
$p$
-adically closed fields of the same rank, the following hold.-
∙
 $\tilde{k}|k\mapsto N\tilde{k}$
defines a bijection from the set of algebraic extensions
$\tilde{k}|k\mapsto N\tilde{k}$
defines a bijection from the set of algebraic extensions
 $\tilde{k}|k$
of
$\tilde{k}|k$
of
 $k$
onto the set of algebraic extensions of
$k$
onto the set of algebraic extensions of
 $N$
.
$N$
. -
∙ The canonical projection
 $G_{N}\rightarrow G_{k}$
is an isomorphism.
$G_{N}\rightarrow G_{k}$
is an isomorphism.
-
-
(e) In particular, if
 $L|l$
is an extension of
$L|l$
is an extension of
 $p$
-adically closed fields of the same rank, in the notation from the Introduction, the following canonical projections are isomorphisms:
$p$
-adically closed fields of the same rank, in the notation from the Introduction, the following canonical projections are isomorphisms: 
-
(D) Valuations and rigid elements
We recall the result of Arason et al. [Reference Arason, Elman and JacobAEJ87, Theorem 2.16]; see also Koenigsmann [Reference KoenigsmannKoe95], Ware [Reference WareWar81], Efrat [Reference EfratEfr99], and especially Topaz [Reference TopazTop15] for much more about this. The point is that one can recover valuations of a field
![]() $K$
from particular subgroups
$K$
from particular subgroups
![]() $T\subset K^{\times }$
as follows: let
$T\subset K^{\times }$
as follows: let
![]() $T\subset K^{\times }$
be a subgroup with
$T\subset K^{\times }$
be a subgroup with
![]() $-1\in T$
. We say that
$-1\in T$
. We say that
![]() $x\in K^{\times }\backslash T$
is
$x\in K^{\times }\backslash T$
is
![]() $T$
-rigid if
$T$
-rigid if
![]() $1+x\in T\cup xT$
; and, by abuse of language, we say that
$1+x\in T\cup xT$
; and, by abuse of language, we say that
![]() $K$
is
$K$
is
![]() $T$
-rigid if all
$T$
-rigid if all
![]() $x\in K^{\times }\backslash T$
are
$x\in K^{\times }\backslash T$
are
![]() $T$
-rigid.
$T$
-rigid.
Theorem 3 (Arason et al.).
In the above notation, let
![]() $T\subset K^{\times }$
be a subgroup with
$T\subset K^{\times }$
be a subgroup with
![]() $-1\in T$
such that
$-1\in T$
such that
![]() $K$
is
$K$
is
![]() $T$
-rigid. Then there exists a valuation
$T$
-rigid. Then there exists a valuation
![]() $v$
of
$v$
of
![]() $K$
whose valuation ideal
$K$
whose valuation ideal
![]() $\mathfrak{m}_{v}$
satisfies
$\mathfrak{m}_{v}$
satisfies
![]() $1+\mathfrak{m}_{v}\subseteq T$
, and whose valuation ring
$1+\mathfrak{m}_{v}\subseteq T$
, and whose valuation ring
![]() ${\mathcal{O}}_{v}$
has the property that
${\mathcal{O}}_{v}$
has the property that
![]() $|{\mathcal{O}}_{v}^{\times }/(T\cap {\mathcal{O}}_{v}^{\times })|\leqslant 2$
.
$|{\mathcal{O}}_{v}^{\times }/(T\cap {\mathcal{O}}_{v}^{\times })|\leqslant 2$
.
3 Proof of Theorem B
To (1): Let
![]() $\widehat{K},\widehat{w}$
be a
$\widehat{K},\widehat{w}$
be a
![]() $p$
-adic closure of
$p$
-adic closure of
![]() $K,w$
. Then
$K,w$
. Then
![]() $\widehat{w}$
prolongs
$\widehat{w}$
prolongs
![]() $w$
and has
$w$
and has
![]() $p$
-adic rank
$p$
-adic rank
![]() $d_{\widehat{w}}=d_{w}$
and thus equal to
$d_{\widehat{w}}=d_{w}$
and thus equal to
![]() $d_{v}$
by the fact that
$d_{v}$
by the fact that
![]() $d_{w}=d_{v}$
. Therefore, since
$d_{w}=d_{v}$
. Therefore, since
![]() $k$
is
$k$
is
![]() $p$
-adically closed,
$p$
-adically closed,
![]() $k$
must be relatively algebraically closed in
$k$
must be relatively algebraically closed in
![]() $\widehat{K}$
. We conclude by using (†) from § 2(C)(6)(e), with
$\widehat{K}$
. We conclude by using (†) from § 2(C)(6)(e), with
![]() $l:=k$
and
$l:=k$
and
![]() $L:=\widehat{K}$
, and taking into account that the isomorphism
$L:=\widehat{K}$
, and taking into account that the isomorphism
![]() $\operatorname{Gal}(\widehat{K}^{\prime \prime }|\widehat{K})\rightarrow \operatorname{Gal}(k^{\prime \prime }|k)$
factors through
$\operatorname{Gal}(\widehat{K}^{\prime \prime }|\widehat{K})\rightarrow \operatorname{Gal}(k^{\prime \prime }|k)$
factors through
![]() $\operatorname{Gal}(K^{\prime \prime }|K)\rightarrow \operatorname{Gal}(k^{\prime \prime }|k)$
and thus gives rise to a liftable section of
$\operatorname{Gal}(K^{\prime \prime }|K)\rightarrow \operatorname{Gal}(k^{\prime \prime }|k)$
and thus gives rise to a liftable section of
![]() $\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(k^{\prime }|k)$
.
$\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(k^{\prime }|k)$
.
To (2): The proof of assertion (2) is divided into three main steps, whereas the hypothesis
![]() $p>2$
is used only in Step 2. This might be relevant when trying to address the case
$p>2$
is used only in Step 2. This might be relevant when trying to address the case
![]() $p=2$
.
$p=2$
.
Step 1. By Kummer theory,
![]() $\operatorname{pr}_{K}^{\prime }:\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(k^{\prime }|k)$
is Pontrjagin dual to the canonical embedding
$\operatorname{pr}_{K}^{\prime }:\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(k^{\prime }|k)$
is Pontrjagin dual to the canonical embedding
![]() $k^{\times }/p\rightarrow K^{\times }/p$
. Second, given a liftable section
$k^{\times }/p\rightarrow K^{\times }/p$
. Second, given a liftable section
![]() $s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
of
$s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
of
![]() $\operatorname{pr}_{K}^{\prime }$
, it follows by Kummer theory that the Pontrjagin dual of
$\operatorname{pr}_{K}^{\prime }$
, it follows by Kummer theory that the Pontrjagin dual of
![]() $s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
is a surjective projection
$s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
is a surjective projection
![]() $K^{\times }/p\rightarrow k^{\times }/p$
, whose kernel
$K^{\times }/p\rightarrow k^{\times }/p$
, whose kernel
![]() $\unicode[STIX]{x1D6F4}/p\subset K^{\times }/p$
is a complement of
$\unicode[STIX]{x1D6F4}/p\subset K^{\times }/p$
is a complement of
![]() $k^{\times }/p\subset K^{\times }/p$
. That means that
$k^{\times }/p\subset K^{\times }/p$
. That means that
![]() $s^{\prime }$
gives rise canonically to a presentation of
$s^{\prime }$
gives rise canonically to a presentation of
![]() $K^{\times }/p$
as a direct sum
$K^{\times }/p$
as a direct sum
For every
![]() $k$
-subfield
$k$
-subfield
![]() $K_{\unicode[STIX]{x1D6FC}}\subset K$
which is relatively algebraically closed in
$K_{\unicode[STIX]{x1D6FC}}\subset K$
which is relatively algebraically closed in
![]() $K$
, one has a commutative diagram of surjective projections
$K$
, one has a commutative diagram of surjective projections

and
![]() $s^{\prime }$
gives rise canonically to a liftable section
$s^{\prime }$
gives rise canonically to a liftable section
![]() $s_{\unicode[STIX]{x1D6FC}}^{\prime }$
of
$s_{\unicode[STIX]{x1D6FC}}^{\prime }$
of
![]() $\operatorname{pr}_{\unicode[STIX]{x1D6FC}}^{\prime }:\operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})\rightarrow \operatorname{Gal}(k^{\prime }|k)$
, etc. In particular, one has corresponding canonical presentations as direct sums
$\operatorname{pr}_{\unicode[STIX]{x1D6FC}}^{\prime }:\operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})\rightarrow \operatorname{Gal}(k^{\prime }|k)$
, etc. In particular, one has corresponding canonical presentations as direct sums
defined by the sections
![]() $s_{\unicode[STIX]{x1D6FC}}^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})$
induced by
$s_{\unicode[STIX]{x1D6FC}}^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})$
induced by
![]() $s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
.
$s^{\prime }:\operatorname{Gal}(k^{\prime }|k)\rightarrow \operatorname{Gal}(K^{\prime }|K)$
.
Claim.
In the above notions, one has
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p=\unicode[STIX]{x1D6F4}/p\cap K_{\unicode[STIX]{x1D6FC}}^{\times }/p$
and thus
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p=\unicode[STIX]{x1D6F4}/p\cap K_{\unicode[STIX]{x1D6FC}}^{\times }/p$
and thus
![]() $\unicode[STIX]{x1D6F4}/p$
determines
$\unicode[STIX]{x1D6F4}/p$
determines
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p$
.
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p$
.
Indeed, let
![]() $D_{\unicode[STIX]{x1D6FC}}:=\operatorname{im}(s_{\unicode[STIX]{x1D6FC}}^{\prime })\subset \operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})$
. Then, by the definition of
$D_{\unicode[STIX]{x1D6FC}}:=\operatorname{im}(s_{\unicode[STIX]{x1D6FC}}^{\prime })\subset \operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})$
. Then, by the definition of
![]() $s_{\unicode[STIX]{x1D6FC}}^{\prime }$
, it follows that
$s_{\unicode[STIX]{x1D6FC}}^{\prime }$
, it follows that
![]() $D_{\unicode[STIX]{x1D6FC}}$
is the image of
$D_{\unicode[STIX]{x1D6FC}}$
is the image of
![]() $D=\operatorname{im}(s^{\prime })$
under the canonical projection
$D=\operatorname{im}(s^{\prime })$
under the canonical projection
![]() $\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})$
. In other words, by Pontrjagin duality, the projection
$\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(K_{\unicode[STIX]{x1D6FC}}^{\prime }|K_{\unicode[STIX]{x1D6FC}})$
. In other words, by Pontrjagin duality, the projection
![]() $K_{\unicode[STIX]{x1D6FC}}^{\times }/p\rightarrow k^{\times }/p$
factors through the inclusion
$K_{\unicode[STIX]{x1D6FC}}^{\times }/p\rightarrow k^{\times }/p$
factors through the inclusion
![]() $K_{\unicode[STIX]{x1D6FC}}^{\times }/p{\hookrightarrow}K^{\times }/p$
. Hence,
$K_{\unicode[STIX]{x1D6FC}}^{\times }/p{\hookrightarrow}K^{\times }/p$
. Hence,
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p$
is mapped into
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p$
is mapped into
![]() $\unicode[STIX]{x1D6F4}/p$
under
$\unicode[STIX]{x1D6F4}/p$
under
![]() $K_{\unicode[STIX]{x1D6FC}}^{\times }/p{\hookrightarrow}K^{\times }/p$
, which proves the claim.
$K_{\unicode[STIX]{x1D6FC}}^{\times }/p{\hookrightarrow}K^{\times }/p$
, which proves the claim.
Now let
![]() $T/p:=\unicode[STIX]{x1D6F4}/p\cdot {\mathcal{O}}_{v}^{\times }/p$
and
$T/p:=\unicode[STIX]{x1D6F4}/p\cdot {\mathcal{O}}_{v}^{\times }/p$
and
![]() $T\subset K^{\times }$
be the corresponding subgroup (thus containing the
$T\subset K^{\times }$
be the corresponding subgroup (thus containing the
![]() $p$
th powers in
$p$
th powers in
![]() $K^{\times }$
). Then, for every
$K^{\times }$
). Then, for every
![]() $k$
-subfield
$k$
-subfield
![]() $K_{\unicode[STIX]{x1D6FC}}\subset K$
which is relatively algebraically closed in
$K_{\unicode[STIX]{x1D6FC}}\subset K$
which is relatively algebraically closed in
![]() $K$
, by the remarks above one has that
$K$
, by the remarks above one has that
![]() $T_{\unicode[STIX]{x1D6FC}}:=T\cap K_{\unicode[STIX]{x1D6FC}}^{\times }\subset K_{\unicode[STIX]{x1D6FC}}^{\times }$
satisfies
$T_{\unicode[STIX]{x1D6FC}}:=T\cap K_{\unicode[STIX]{x1D6FC}}^{\times }\subset K_{\unicode[STIX]{x1D6FC}}^{\times }$
satisfies
![]() $T_{\unicode[STIX]{x1D6FC}}/p=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p\cdot {\mathcal{O}}_{v}^{\times }/p$
.
$T_{\unicode[STIX]{x1D6FC}}/p=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}/p\cdot {\mathcal{O}}_{v}^{\times }/p$
.
Finally, let
![]() $(K_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}}$
be the family of all the
$(K_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}}$
be the family of all the
![]() $k$
-subfields
$k$
-subfields
![]() $K_{\unicode[STIX]{x1D6FC}}\subset K$
which are relatively algebraically closed in
$K_{\unicode[STIX]{x1D6FC}}\subset K$
which are relatively algebraically closed in
![]() $K$
and satisfy
$K$
and satisfy
![]() $\text{tr}.\text{deg}(K_{\unicode[STIX]{x1D6FC}}|k)=1$
. Then, by Pop [Reference PopPop10, Theorem B], for every subfield
$\text{tr}.\text{deg}(K_{\unicode[STIX]{x1D6FC}}|k)=1$
. Then, by Pop [Reference PopPop10, Theorem B], for every subfield
![]() $K_{\unicode[STIX]{x1D6FC}}$
, there exists a unique
$K_{\unicode[STIX]{x1D6FC}}$
, there exists a unique
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $w_{\unicode[STIX]{x1D6FC}}$
of
$w_{\unicode[STIX]{x1D6FC}}$
of
![]() $K_{\unicode[STIX]{x1D6FC}}$
prolonging the
$K_{\unicode[STIX]{x1D6FC}}$
prolonging the
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $v$
of
$v$
of
![]() $k$
to
$k$
to
![]() $K_{\unicode[STIX]{x1D6FC}}$
and having the same
$K_{\unicode[STIX]{x1D6FC}}$
and having the same
![]() $p$
-adic rank as
$p$
-adic rank as
![]() $v$
. Our final aim is to show that there exists a (unique)
$v$
. Our final aim is to show that there exists a (unique)
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $w$
of
$w$
of
![]() $K$
such that
$K$
such that
![]() $w_{\unicode[STIX]{x1D6FC}}$
is the restriction of
$w_{\unicode[STIX]{x1D6FC}}$
is the restriction of
![]() $w$
to
$w$
to
![]() $K_{\unicode[STIX]{x1D6FC}}$
for each
$K_{\unicode[STIX]{x1D6FC}}$
for each
![]() $K_{\unicode[STIX]{x1D6FC}}$
.
$K_{\unicode[STIX]{x1D6FC}}$
.
Lemma 4. In the above notation,
![]() $K_{\unicode[STIX]{x1D6FC}}$
is
$K_{\unicode[STIX]{x1D6FC}}$
is
![]() $T_{\unicode[STIX]{x1D6FC}}$
-rigid. Further,
$T_{\unicode[STIX]{x1D6FC}}$
-rigid. Further,
![]() $T=\bigcup _{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$
, and
$T=\bigcup _{\unicode[STIX]{x1D6FC}}T_{\unicode[STIX]{x1D6FC}}$
, and
![]() $K$
is
$K$
is
![]() $T$
-rigid.
$T$
-rigid.
Proof. We first show that
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}\subset T_{\unicode[STIX]{x1D6FC}}$
. Indeed, let
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}\subset T_{\unicode[STIX]{x1D6FC}}$
. Indeed, let
![]() $v$
be the
$v$
be the
![]() $p$
-adic valuation of
$p$
-adic valuation of
![]() $k$
, and further consider: first, the canonical coarsening
$k$
, and further consider: first, the canonical coarsening
![]() $v_{1}$
of
$v_{1}$
of
![]() $v$
and the canonical
$v$
and the canonical
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $v_{0}:=v/v_{1}$
on the residue field
$v_{0}:=v/v_{1}$
on the residue field
![]() $k_{0}:=kv_{1}$
of
$k_{0}:=kv_{1}$
of
![]() $v_{1}$
. Second, consider the
$v_{1}$
. Second, consider the
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $w_{\unicode[STIX]{x1D6FC}}$
of
$w_{\unicode[STIX]{x1D6FC}}$
of
![]() $K_{\unicode[STIX]{x1D6FC}}$
, and let
$K_{\unicode[STIX]{x1D6FC}}$
, and let
![]() $w_{\unicode[STIX]{x1D6FC}1}$
and
$w_{\unicode[STIX]{x1D6FC}1}$
and
![]() $w_{\unicode[STIX]{x1D6FC}0}:=w_{\unicode[STIX]{x1D6FC}}/w_{\unicode[STIX]{x1D6FC}1}$
and
$w_{\unicode[STIX]{x1D6FC}0}:=w_{\unicode[STIX]{x1D6FC}}/w_{\unicode[STIX]{x1D6FC}1}$
and
![]() $K_{\unicode[STIX]{x1D6FC}0}$
be correspondingly defined. Notice that
$K_{\unicode[STIX]{x1D6FC}0}$
be correspondingly defined. Notice that
![]() $w_{\unicode[STIX]{x1D6FC}}|_{k}=v$
implies that
$w_{\unicode[STIX]{x1D6FC}}|_{k}=v$
implies that
![]() $w_{\unicode[STIX]{x1D6FC}1}|_{k}=v_{1}$
and
$w_{\unicode[STIX]{x1D6FC}1}|_{k}=v_{1}$
and
![]() $w_{\unicode[STIX]{x1D6FC}0}|_{k_{0}}=v_{0}$
. The following hold.
$w_{\unicode[STIX]{x1D6FC}0}|_{k_{0}}=v_{0}$
. The following hold.
-
(a) First, by Fact 2, it follows that
 $\sqrt[p]{1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}}$
is contained in the decomposition field of
$\sqrt[p]{1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}}$
is contained in the decomposition field of
 $w_{\unicode[STIX]{x1D6FC}}$
over
$w_{\unicode[STIX]{x1D6FC}}$
over
 $K$
, which is actually the fixed field of
$K$
, which is actually the fixed field of
 $Z_{w_{\unicode[STIX]{x1D6FC}}}$
in
$Z_{w_{\unicode[STIX]{x1D6FC}}}$
in
 $K_{\unicode[STIX]{x1D6FC}}^{\prime }$
. Second, the fixed field of
$K_{\unicode[STIX]{x1D6FC}}^{\prime }$
. Second, the fixed field of
 $\operatorname{im}(s^{\prime })$
in
$\operatorname{im}(s^{\prime })$
in
 $K_{\unicode[STIX]{x1D6FC}}^{\prime }$
is, by the mere definitions, generated as a field extension of
$K_{\unicode[STIX]{x1D6FC}}^{\prime }$
is, by the mere definitions, generated as a field extension of
 $K$
by
$K$
by
 $\sqrt[p]{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}^{^{\prime }}}$
. Thus, since
$\sqrt[p]{\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}^{^{\prime }}}$
. Thus, since
 $\operatorname{im}(s^{\prime })\subset Z_{w_{\unicode[STIX]{x1D6FC}}}$
, it follows by Kummer theory that
$\operatorname{im}(s^{\prime })\subset Z_{w_{\unicode[STIX]{x1D6FC}}}$
, it follows by Kummer theory that
 $1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}\subset \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
.
$1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}\subset \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
. -
(b) Since, by the mere definition, one has
 $\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}}\subset \mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
and
$\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}}\subset \mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
and
 $p$
is invertible in
$p$
is invertible in
 ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}$
, it follows that
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}$
, it follows that
 $1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}}\subset 1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
. Thus, one has finally
$1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}}\subset 1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
. Thus, one has finally
 $1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}}\subset \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
as well.
$1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}}\subset \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
as well. -
(c) Since
 $w_{\unicode[STIX]{x1D6FC}}$
and
$w_{\unicode[STIX]{x1D6FC}}$
and
 $v$
have the same
$v$
have the same
 $p$
-adic rank, it follows by the discussion in § 2(C)(5) that
$p$
-adic rank, it follows by the discussion in § 2(C)(5) that
 $w_{\unicode[STIX]{x1D6FC}0}$
and
$w_{\unicode[STIX]{x1D6FC}0}$
and
 $v_{0}$
are discrete
$v_{0}$
are discrete
 $p$
-adic valuations of the same
$p$
-adic valuations of the same
 $p$
-adic rank and hence
$p$
-adic rank and hence
 $k_{0}$
is dense in
$k_{0}$
is dense in
 $K_{\unicode[STIX]{x1D6FC}0}$
. Therefore, since
$K_{\unicode[STIX]{x1D6FC}0}$
. Therefore, since
 $w_{\unicode[STIX]{x1D6FC}0}|v_{0}$
are discrete valuations, and
$w_{\unicode[STIX]{x1D6FC}0}|v_{0}$
are discrete valuations, and
 $k_{0}$
is dense in
$k_{0}$
is dense in
 $K_{\unicode[STIX]{x1D6FC}0}$
under
$K_{\unicode[STIX]{x1D6FC}0}$
under
 $k_{0}{\hookrightarrow}K_{\unicode[STIX]{x1D6FC}0}$
, one has that
$k_{0}{\hookrightarrow}K_{\unicode[STIX]{x1D6FC}0}$
, one has that
 ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}0}}^{\times }={\mathcal{O}}_{v_{0}}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
and
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}0}}^{\times }={\mathcal{O}}_{v_{0}}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
and
 $K_{\unicode[STIX]{x1D6FC}0}^{\times }=k_{0}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
as well.
$K_{\unicode[STIX]{x1D6FC}0}^{\times }=k_{0}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
as well. -
(d) Since
 $K_{\unicode[STIX]{x1D6FC}0}^{\times }={\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }/(1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}})$
,
$K_{\unicode[STIX]{x1D6FC}0}^{\times }={\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }/(1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}})$
,
 $k_{0}^{\times }={\mathcal{O}}_{v_{1}}^{\times }/(1+\mathfrak{m}_{v_{1}})$
, and
$k_{0}^{\times }={\mathcal{O}}_{v_{1}}^{\times }/(1+\mathfrak{m}_{v_{1}})$
, and
 $1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}}=(1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})/(1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}})$
, from the equality
$1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}}=(1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})/(1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}})$
, from the equality
 $K_{\unicode[STIX]{x1D6FC}0}^{\times }=k_{0}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
above, it follows that
$K_{\unicode[STIX]{x1D6FC}0}^{\times }=k_{0}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
above, it follows that
 ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }={\mathcal{O}}_{v_{1}}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})$
.
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }={\mathcal{O}}_{v_{1}}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})$
. -
(e) Similarly, the equalities
 ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}0}}^{\times }={\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }/(1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}})$
and
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}0}}^{\times }={\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }/(1+\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}1}})$
and
 ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}0}}^{\times }={\mathcal{O}}_{v_{0}}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
imply that
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}0}}^{\times }={\mathcal{O}}_{v_{0}}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}0}})$
imply that
 ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }={\mathcal{O}}_{v}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})$
.
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }={\mathcal{O}}_{v}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})$
.
Hence, since
![]() ${\mathcal{O}}_{v}^{\times },1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}\subset T_{\unicode[STIX]{x1D6FC}}$
, one finally has
${\mathcal{O}}_{v}^{\times },1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}\subset T_{\unicode[STIX]{x1D6FC}}$
, one finally has
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }={\mathcal{O}}_{v}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})\subset T_{\unicode[STIX]{x1D6FC}}$
, as claimed.
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }={\mathcal{O}}_{v}^{\times }\cdot (1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}})\subset T_{\unicode[STIX]{x1D6FC}}$
, as claimed.
We next show that
![]() $K_{\unicode[STIX]{x1D6FC}}$
is
$K_{\unicode[STIX]{x1D6FC}}$
is
![]() $T_{\unicode[STIX]{x1D6FC}}$
-rigid. To do so, we first notice that by the discussion above, for any fixed element
$T_{\unicode[STIX]{x1D6FC}}$
-rigid. To do so, we first notice that by the discussion above, for any fixed element
![]() $\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{v}$
of minimal positive value
$\unicode[STIX]{x1D70B}\in {\mathcal{O}}_{v}$
of minimal positive value
![]() $1_{v}\in vk$
, the following holds: let
$1_{v}\in vk$
, the following holds: let
![]() $x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }$
be an arbitrary
$x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }$
be an arbitrary
![]() $w_{\unicode[STIX]{x1D6FC}1}$
-unit. Then there exist
$w_{\unicode[STIX]{x1D6FC}1}$
-unit. Then there exist
![]() $m\in \mathbb{Z}$
,
$m\in \mathbb{Z}$
,
![]() $\unicode[STIX]{x1D716}\in {\mathcal{O}}_{v}^{\times }$
, and
$\unicode[STIX]{x1D716}\in {\mathcal{O}}_{v}^{\times }$
, and
![]() $x_{1}\in 1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
such that
$x_{1}\in 1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
such that
Now let
![]() $x\in K_{\unicode[STIX]{x1D6FC}}^{\times }\backslash T_{\unicode[STIX]{x1D6FC}}$
be given. Then one has the following possibilities.
$x\in K_{\unicode[STIX]{x1D6FC}}^{\times }\backslash T_{\unicode[STIX]{x1D6FC}}$
be given. Then one has the following possibilities.
-
(1)
 $w_{\unicode[STIX]{x1D6FC}1}(x)>0$
. Then
$w_{\unicode[STIX]{x1D6FC}1}(x)>0$
. Then
 $1+x$
is a principal
$1+x$
is a principal
 $w_{\unicode[STIX]{x1D6FC}1}$
-unit and, therefore,
$w_{\unicode[STIX]{x1D6FC}1}$
-unit and, therefore,
 $1+x\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
by assertion (b) above. Since
$1+x\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
by assertion (b) above. Since
 $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\subset T_{\unicode[STIX]{x1D6FC}}$
, we conclude that
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}\subset T_{\unicode[STIX]{x1D6FC}}$
, we conclude that
 $1+x\in T_{\unicode[STIX]{x1D6FC}}$
.
$1+x\in T_{\unicode[STIX]{x1D6FC}}$
. -
(2)
 $w_{\unicode[STIX]{x1D6FC}1}(x)<0$
. Then
$w_{\unicode[STIX]{x1D6FC}1}(x)<0$
. Then
 $1+x=x(1+x^{-1})$
. Since
$1+x=x(1+x^{-1})$
. Since
 $w_{\unicode[STIX]{x1D6FC}1}(x^{-1})>0$
, by the discussion above, it follows that
$w_{\unicode[STIX]{x1D6FC}1}(x^{-1})>0$
, by the discussion above, it follows that
 $1+x^{-1}\in T_{\unicode[STIX]{x1D6FC}}$
. Therefore, one finally has that
$1+x^{-1}\in T_{\unicode[STIX]{x1D6FC}}$
. Therefore, one finally has that
 $1+x\in xT_{\unicode[STIX]{x1D6FC}}$
.
$1+x\in xT_{\unicode[STIX]{x1D6FC}}$
. -
(3)
 $w_{\unicode[STIX]{x1D6FC}1}(x)=0$
or, equivalently,
$w_{\unicode[STIX]{x1D6FC}1}(x)=0$
or, equivalently,
 $x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }$
. Let
$x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}1}}^{\times }$
. Let
 $x=\unicode[STIX]{x1D70B}^{m}\unicode[STIX]{x1D716}x_{1}$
be as given in (♯) above. One has:
$x=\unicode[STIX]{x1D70B}^{m}\unicode[STIX]{x1D716}x_{1}$
be as given in (♯) above. One has:
-
 $(\unicode[STIX]{x1D6FC})$
$(\unicode[STIX]{x1D6FC})$
-
if
 $m>0$
, then
$m>0$
, then
 $x\in \unicode[STIX]{x1D70B}^{m}\cdot {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }$
and thus
$x\in \unicode[STIX]{x1D70B}^{m}\cdot {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }$
and thus
 $1+x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }$
as well. Hence, by the relation (♯) above,
$1+x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }$
as well. Hence, by the relation (♯) above,
 $1+x=\unicode[STIX]{x1D702}_{1}\cdot \unicode[STIX]{x1D702}_{0}$
for some
$1+x=\unicode[STIX]{x1D702}_{1}\cdot \unicode[STIX]{x1D702}_{0}$
for some
 $\unicode[STIX]{x1D702}_{1}\in 1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}\subset \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
,
$\unicode[STIX]{x1D702}_{1}\in 1+p^{2}\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}\subset \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FC}}$
,
 $\unicode[STIX]{x1D702}_{0}\in {\mathcal{O}}_{v}^{\times }$
. Thus, finally,
$\unicode[STIX]{x1D702}_{0}\in {\mathcal{O}}_{v}^{\times }$
. Thus, finally,
 $1+x\in T_{\unicode[STIX]{x1D6FC}}$
;
$1+x\in T_{\unicode[STIX]{x1D6FC}}$
; -
 $(\unicode[STIX]{x1D6FD})$
$(\unicode[STIX]{x1D6FD})$
-
if
 $m<0$
, then
$m<0$
, then
 $1+x=x(1+x^{-1})$
, and
$1+x=x(1+x^{-1})$
, and
 $x^{-1}$
has value
$x^{-1}$
has value
 $-m>0$
. But then, by the first case above,
$-m>0$
. But then, by the first case above,
 $1+x^{-1}\in T_{\unicode[STIX]{x1D6FC}}$
. Hence,
$1+x^{-1}\in T_{\unicode[STIX]{x1D6FC}}$
. Hence,
 $1+x=x(1+x^{-1})\in xT_{\unicode[STIX]{x1D6FC}}$
and thus
$1+x=x(1+x^{-1})\in xT_{\unicode[STIX]{x1D6FC}}$
and thus
 $1+x\in xT_{\unicode[STIX]{x1D6FC}}$
;
$1+x\in xT_{\unicode[STIX]{x1D6FC}}$
; -
 $(\unicode[STIX]{x1D6FE})$
$(\unicode[STIX]{x1D6FE})$
-
if
 $m=0$
, then
$m=0$
, then
 $x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }\subset T_{\unicode[STIX]{x1D6FC}}$
and thus
$x\in {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }\subset T_{\unicode[STIX]{x1D6FC}}$
and thus
 $x\not \in K_{\unicode[STIX]{x1D6FC}}^{\times }\backslash T_{\unicode[STIX]{x1D6FC}}$
.
$x\not \in K_{\unicode[STIX]{x1D6FC}}^{\times }\backslash T_{\unicode[STIX]{x1D6FC}}$
.
For the
![]() $T$
-rigidity of
$T$
-rigidity of
![]() $K$
, let
$K$
, let
![]() $x\in K\backslash T$
be given. If
$x\in K\backslash T$
be given. If
![]() $x\in k$
, then
$x\in k$
, then
![]() $x\in k\backslash {\mathcal{O}}_{v}^{\times }$
(by the definition of
$x\in k\backslash {\mathcal{O}}_{v}^{\times }$
(by the definition of
![]() $T$
). An easy case by case analysis, namely
$T$
). An easy case by case analysis, namely
![]() $v(x)>0$
or
$v(x)>0$
or
![]() $v(x)<0$
, shows that
$v(x)<0$
, shows that
![]() $1+x\in {\mathcal{O}}_{v}^{\times }\cup x{\mathcal{O}}_{v}^{\times }$
, etc. Finally, if
$1+x\in {\mathcal{O}}_{v}^{\times }\cup x{\mathcal{O}}_{v}^{\times }$
, etc. Finally, if
![]() $x\not \in k$
, then letting
$x\not \in k$
, then letting
![]() $K_{\unicode[STIX]{x1D6FC}}\subset K$
be the relative algebraic closure of
$K_{\unicode[STIX]{x1D6FC}}\subset K$
be the relative algebraic closure of
![]() $k(x)$
in
$k(x)$
in
![]() $K$
, one has: since
$K$
, one has: since
![]() $x\in K\backslash T$
, one must have
$x\in K\backslash T$
, one must have
![]() $x\in K_{\unicode[STIX]{x1D6FC}}\backslash T_{\unicode[STIX]{x1D6FC}}$
. Thus, by the discussion above, it follows that
$x\in K_{\unicode[STIX]{x1D6FC}}\backslash T_{\unicode[STIX]{x1D6FC}}$
. Thus, by the discussion above, it follows that
![]() $1+x\in T_{\unicode[STIX]{x1D6FC}}\cup xT_{\unicode[STIX]{x1D6FC}}$
and, therefore,
$1+x\in T_{\unicode[STIX]{x1D6FC}}\cup xT_{\unicode[STIX]{x1D6FC}}$
and, therefore,
![]() $1+x\in T\cup xT$
, etc.
$1+x\in T\cup xT$
, etc.
This concludes the proof of Lemma 4. ◻
Step 2. Using Lemma 4 above and applying the Arason–Elman–Jacob theorem 3, we get: there exists a valuation
![]() $w$
on
$w$
on
![]() $K$
such that
$K$
such that
![]() $|{\mathcal{O}}_{w}^{\times }/({\mathcal{O}}_{w}\cap T)|\leqslant 2$
and
$|{\mathcal{O}}_{w}^{\times }/({\mathcal{O}}_{w}\cap T)|\leqslant 2$
and
![]() $1+\mathfrak{m}_{w}\subset T$
. Hence, letting
$1+\mathfrak{m}_{w}\subset T$
. Hence, letting
![]() ${\mathcal{O}}_{w}^{\times }T\subset K^{\times }$
be the subgroup generated by
${\mathcal{O}}_{w}^{\times }T\subset K^{\times }$
be the subgroup generated by
![]() $T$
and
$T$
and
![]() ${\mathcal{O}}_{w}$
, one has
${\mathcal{O}}_{w}$
, one has
![]() ${\mathcal{O}}_{w}/({\mathcal{O}}_{w}\cap T)=({\mathcal{O}}_{w}^{\times }T)/T$
and thus
${\mathcal{O}}_{w}/({\mathcal{O}}_{w}\cap T)=({\mathcal{O}}_{w}^{\times }T)/T$
and thus
![]() $|({\mathcal{O}}_{w}^{\times }T)/T|\leqslant 2$
. We claim that
$|({\mathcal{O}}_{w}^{\times }T)/T|\leqslant 2$
. We claim that
![]() ${\mathcal{O}}_{w}^{\times }\subset T$
. Indeed, first, one has
${\mathcal{O}}_{w}^{\times }\subset T$
. Indeed, first, one has
![]() $k^{\times }={\mathcal{O}}_{v}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
as direct sum and hence
$k^{\times }={\mathcal{O}}_{v}^{\times }\cdot \unicode[STIX]{x1D70B}^{\mathbb{Z}}$
as direct sum and hence
![]() $(k^{\times }/p)/({\mathcal{O}}_{v}^{\times }/p)=\unicode[STIX]{x1D70B}^{\mathbb{Z}/p}$
. Second, by definitions, one has that
$(k^{\times }/p)/({\mathcal{O}}_{v}^{\times }/p)=\unicode[STIX]{x1D70B}^{\mathbb{Z}/p}$
. Second, by definitions, one has that
![]() $K^{\times }/p=\unicode[STIX]{x1D6F4}/p\cdot k^{\times }/p$
and
$K^{\times }/p=\unicode[STIX]{x1D6F4}/p\cdot k^{\times }/p$
and
![]() $T/p=\unicode[STIX]{x1D6F4}/p\cdot {\mathcal{O}}_{v}^{\times }/p$
, both of which being direct sums. Thus, finally one gets that
$T/p=\unicode[STIX]{x1D6F4}/p\cdot {\mathcal{O}}_{v}^{\times }/p$
, both of which being direct sums. Thus, finally one gets that
where the dot denotes direct sums; in particular, one has
![]() $|K^{\times }/T|=|(K^{\times }/p)/(T/p)|=p$
. Hence, considering the canonical inclusions of groups
$|K^{\times }/T|=|(K^{\times }/p)/(T/p)|=p$
. Hence, considering the canonical inclusions of groups
![]() $T\subseteq {\mathcal{O}}_{w}^{\times }T\subseteq K^{\times }$
, we get
$T\subseteq {\mathcal{O}}_{w}^{\times }T\subseteq K^{\times }$
, we get
Since
![]() $|({\mathcal{O}}_{w}^{\times }T)/T|\leqslant 2$
and
$|({\mathcal{O}}_{w}^{\times }T)/T|\leqslant 2$
and
![]() $2<p$
, it follows that
$2<p$
, it follows that
![]() $|({\mathcal{O}}_{w}^{\times }T)/T|=1$
is the only possibility; hence,
$|({\mathcal{O}}_{w}^{\times }T)/T|=1$
is the only possibility; hence,
![]() $T={\mathcal{O}}_{w}^{\times }T$
, and, finally,
$T={\mathcal{O}}_{w}^{\times }T$
, and, finally,
![]() ${\mathcal{O}}_{w}^{\times }\subseteq T$
. Hence, we conclude that
${\mathcal{O}}_{w}^{\times }\subseteq T$
. Hence, we conclude that
![]() $|K^{\times }/{\mathcal{O}}_{w}^{\times }|\geqslant p$
and therefore we have the following result.
$|K^{\times }/{\mathcal{O}}_{w}^{\times }|\geqslant p$
and therefore we have the following result.
![]() $\bullet$
The valuation
$\bullet$
The valuation
![]() $w$
is a non-trivial valuation of
$w$
is a non-trivial valuation of
![]() $K$
.
$K$
.
Step 3. Recalling that
![]() ${\mathcal{O}}_{w}^{\times }\subset T$
, one has that the canonical projection
${\mathcal{O}}_{w}^{\times }\subset T$
, one has that the canonical projection
![]() $K^{\times }/{\mathcal{O}}_{w}^{\times }\rightarrow K^{\times }/T$
is surjective. Therefore, if
$K^{\times }/{\mathcal{O}}_{w}^{\times }\rightarrow K^{\times }/T$
is surjective. Therefore, if
![]() $b\in K$
is a generator of
$b\in K$
is a generator of
![]() $K^{\times }/T$
, e.g.,
$K^{\times }/T$
, e.g.,
![]() $b=\unicode[STIX]{x1D70B}\in k_{0}$
has
$b=\unicode[STIX]{x1D70B}\in k_{0}$
has
![]() $v_{0}(\unicode[STIX]{x1D70B})=1$
, then
$v_{0}(\unicode[STIX]{x1D70B})=1$
, then
![]() $b$
is not a
$b$
is not a
![]() $w$
-unit and
$w$
-unit and
![]() $w(b)$
is not divisible by
$w(b)$
is not divisible by
![]() $p$
in
$p$
in
![]() $wK=K^{\times }/{\mathcal{O}}_{w}^{\times }$
and hence
$wK=K^{\times }/{\mathcal{O}}_{w}^{\times }$
and hence
![]() $wK$
is not divisible by
$wK$
is not divisible by
![]() $p$
.
$p$
.
For every subfield
![]() $K_{\unicode[STIX]{x1D6FC}}\subset K$
as in the proof of Lemma 4, let
$K_{\unicode[STIX]{x1D6FC}}\subset K$
as in the proof of Lemma 4, let
![]() $v_{\unicode[STIX]{x1D6FC}}:=w|_{K_{\unicode[STIX]{x1D6FC}}}$
be the restriction of
$v_{\unicode[STIX]{x1D6FC}}:=w|_{K_{\unicode[STIX]{x1D6FC}}}$
be the restriction of
![]() $w$
to
$w$
to
![]() $K_{\unicode[STIX]{x1D6FC}}$
. Then
$K_{\unicode[STIX]{x1D6FC}}$
. Then
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}={\mathcal{O}}_{w}\cap K_{\unicode[STIX]{x1D6FC}}$
and, therefore,
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}={\mathcal{O}}_{w}\cap K_{\unicode[STIX]{x1D6FC}}$
and, therefore,
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }$
is contained in
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }$
is contained in
![]() $T_{\unicode[STIX]{x1D6FC}}=T\cap K_{\unicode[STIX]{x1D6FC}}$
.
$T_{\unicode[STIX]{x1D6FC}}=T\cap K_{\unicode[STIX]{x1D6FC}}$
.
Lemma 5. The restriction
![]() $v_{\unicode[STIX]{x1D6FC}}:=w|_{K_{\unicode[STIX]{x1D6FC}}}$
of
$v_{\unicode[STIX]{x1D6FC}}:=w|_{K_{\unicode[STIX]{x1D6FC}}}$
of
![]() $w$
to
$w$
to
![]() $K_{\unicode[STIX]{x1D6FC}}$
equals the
$K_{\unicode[STIX]{x1D6FC}}$
equals the
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $w_{\unicode[STIX]{x1D6FC}}$
.
$w_{\unicode[STIX]{x1D6FC}}$
.
Proof. By the first part of the proof of Lemma 4, we have that
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }\subset T_{\unicode[STIX]{x1D6FC}}$
. Since
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }\subset T_{\unicode[STIX]{x1D6FC}}$
. Since
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }\subseteq T_{\unicode[STIX]{x1D6FC}}$
as well, it follows that the element-wise product
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }\subseteq T_{\unicode[STIX]{x1D6FC}}$
as well, it follows that the element-wise product
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }{\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }$
is contained in
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }{\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }$
is contained in
![]() $T_{\unicode[STIX]{x1D6FC}}$
. Since
$T_{\unicode[STIX]{x1D6FC}}$
. Since
![]() $T_{\unicode[STIX]{x1D6FC}}$
is a proper subgroup of
$T_{\unicode[STIX]{x1D6FC}}$
is a proper subgroup of
![]() $K_{\unicode[STIX]{x1D6FC}}^{\times }$
, it follows that
$K_{\unicode[STIX]{x1D6FC}}^{\times }$
, it follows that
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }{\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }\neq K^{\times }$
as well. The following is well-known valuation theoretical nonsense: let
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }{\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }\neq K^{\times }$
as well. The following is well-known valuation theoretical nonsense: let
![]() $\mathfrak{n}$
be the largest common ideal of
$\mathfrak{n}$
be the largest common ideal of
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
and
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
and
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
. Then
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
. Then
![]() ${\mathcal{O}}:={\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
equals both the localization of
${\mathcal{O}}:={\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
equals both the localization of
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
at
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
at
![]() $\mathfrak{n}$
and the localization of
$\mathfrak{n}$
and the localization of
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
at
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
at
![]() $\mathfrak{n}$
. Further,
$\mathfrak{n}$
. Further,
![]() ${\mathcal{O}}$
is the smallest valuation ring of
${\mathcal{O}}$
is the smallest valuation ring of
![]() $K$
which contains both
$K$
which contains both
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
and
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
and
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
; or, equivalently,
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
; or, equivalently,
![]() ${\mathcal{O}}$
is the valuation ring of the finest common coarsening of
${\mathcal{O}}$
is the valuation ring of the finest common coarsening of
![]() $v_{\unicode[STIX]{x1D6FC}}$
and
$v_{\unicode[STIX]{x1D6FC}}$
and
![]() $w_{\unicode[STIX]{x1D6FC}}$
. We now claim that one has
$w_{\unicode[STIX]{x1D6FC}}$
. We now claim that one has
Indeed, let
![]() $v_{\unicode[STIX]{x1D6FC}}^{1}$
and
$v_{\unicode[STIX]{x1D6FC}}^{1}$
and
![]() $w_{\unicode[STIX]{x1D6FC}}^{1}$
be the valuations of
$w_{\unicode[STIX]{x1D6FC}}^{1}$
be the valuations of
![]() $\unicode[STIX]{x1D705}(\mathfrak{n}):={\mathcal{O}}/\mathfrak{n}$
defined by
$\unicode[STIX]{x1D705}(\mathfrak{n}):={\mathcal{O}}/\mathfrak{n}$
defined by
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}/\mathfrak{n}$
and
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}/\mathfrak{n}$
and
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}/\mathfrak{n}$
, respectively. Then
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}/\mathfrak{n}$
, respectively. Then
![]() $v_{\unicode[STIX]{x1D6FC}}^{1}$
and
$v_{\unicode[STIX]{x1D6FC}}^{1}$
and
![]() $w_{\unicode[STIX]{x1D6FC}}^{1}$
are independent, and one has exact sequences
$w_{\unicode[STIX]{x1D6FC}}^{1}$
are independent, and one has exact sequences
Since
![]() $v_{\unicode[STIX]{x1D6FC}}^{1}$
and
$v_{\unicode[STIX]{x1D6FC}}^{1}$
and
![]() $w_{\unicode[STIX]{x1D6FC}}^{1}$
are independent valuations of
$w_{\unicode[STIX]{x1D6FC}}^{1}$
are independent valuations of
![]() $\unicode[STIX]{x1D705}(\mathfrak{n})$
, one has that
$\unicode[STIX]{x1D705}(\mathfrak{n})$
, one has that
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}^{1}}^{\times }{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}^{1}}^{\times }=\unicode[STIX]{x1D705}(\mathfrak{n})^{\times }$
and therefore
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}^{1}}^{\times }{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}^{1}}^{\times }=\unicode[STIX]{x1D705}(\mathfrak{n})^{\times }$
and therefore
On the other hand, one also has
![]() ${\mathcal{O}}^{\times }/(1+\mathfrak{n})=\unicode[STIX]{x1D705}(\mathfrak{n})^{\times }$
. Further,
${\mathcal{O}}^{\times }/(1+\mathfrak{n})=\unicode[STIX]{x1D705}(\mathfrak{n})^{\times }$
. Further,
![]() $1+\mathfrak{n}$
is contained in both
$1+\mathfrak{n}$
is contained in both
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }$
and
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }$
and
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }$
and hence we conclude that
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }$
and hence we conclude that
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }={\mathcal{O}}^{\times }$
, as claimed.
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}^{\times }{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}^{\times }={\mathcal{O}}^{\times }$
, as claimed.
By contradiction, suppose that
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}\neq {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
. Recall that the valuation ring
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}\neq {\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
. Recall that the valuation ring
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
has finite residue field and hence
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
has finite residue field and hence
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
is minimal among the valuation rings of
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
is minimal among the valuation rings of
![]() $K_{\unicode[STIX]{x1D6FC}}$
and, in particular,
$K_{\unicode[STIX]{x1D6FC}}$
and, in particular,
![]() ${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
cannot be contained in
${\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
cannot be contained in
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
. Therefore, in the above notation, one has that
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
. Therefore, in the above notation, one has that
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}\subset {\mathcal{O}}$
strictly or, equivalently,
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}\subset {\mathcal{O}}$
strictly or, equivalently,
![]() $\mathfrak{n}\subset \mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
is a strict inclusion. On the other hand, if
$\mathfrak{n}\subset \mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}$
is a strict inclusion. On the other hand, if
![]() $b\in k$
is any element of minimal positive value
$b\in k$
is any element of minimal positive value
![]() $1_{v}$
, then
$1_{v}$
, then
![]() $\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}=b{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
and, therefore,
$\mathfrak{m}_{w_{\unicode[STIX]{x1D6FC}}}=b{\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}$
and, therefore,
![]() $b\not \in \mathfrak{n}$
. Thus, we have
$b\not \in \mathfrak{n}$
. Thus, we have
contradicting the fact that
![]() $w(b)$
generates
$w(b)$
generates
![]() $wK/w(T)\cong \mathbb{Z}/p$
. Thus, we conclude that one must have
$wK/w(T)\cong \mathbb{Z}/p$
. Thus, we conclude that one must have
![]() ${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}={\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
, and Lemma 5 is proved.◻
${\mathcal{O}}_{w_{\unicode[STIX]{x1D6FC}}}={\mathcal{O}}_{v_{\unicode[STIX]{x1D6FC}}}$
, and Lemma 5 is proved.◻
We next claim that
![]() $w$
is a
$w$
is a
![]() $p$
-adic valuation of
$p$
-adic valuation of
![]() $K$
having
$K$
having
![]() $p$
-adic rank
$p$
-adic rank
![]() $d_{w}=d_{v}$
. Indeed, for
$d_{w}=d_{v}$
. Indeed, for
![]() $t\in {\mathcal{O}}_{w}$
, let
$t\in {\mathcal{O}}_{w}$
, let
![]() $K_{\unicode[STIX]{x1D6FC}}\subset K$
be the relative algebraic closure of
$K_{\unicode[STIX]{x1D6FC}}\subset K$
be the relative algebraic closure of
![]() $k(t)$
in
$k(t)$
in
![]() $K$
. Then
$K$
. Then
![]() $K_{\unicode[STIX]{x1D6FC}}|k$
has transcendence degree
$K_{\unicode[STIX]{x1D6FC}}|k$
has transcendence degree
![]() ${\leqslant}1$
and, therefore,
${\leqslant}1$
and, therefore,
![]() $w|_{K_{\unicode[STIX]{x1D6FC}}}=w_{\unicode[STIX]{x1D6FC}}$
is the
$w|_{K_{\unicode[STIX]{x1D6FC}}}=w_{\unicode[STIX]{x1D6FC}}$
is the
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $w_{\unicode[STIX]{x1D6FC}}$
by Lemma 5. In particular, if
$w_{\unicode[STIX]{x1D6FC}}$
by Lemma 5. In particular, if
![]() $b\in k$
is such that
$b\in k$
is such that
![]() $v(b)=1_{v}$
is the minimal positive element of
$v(b)=1_{v}$
is the minimal positive element of
![]() $v(k^{\times })$
, it follows that
$v(k^{\times })$
, it follows that
![]() $w_{\unicode[STIX]{x1D6FC}}(b)$
is the minimal positive element of
$w_{\unicode[STIX]{x1D6FC}}(b)$
is the minimal positive element of
![]() $w_{\unicode[STIX]{x1D6FC}}K_{\unicode[STIX]{x1D6FC}}$
under
$w_{\unicode[STIX]{x1D6FC}}K_{\unicode[STIX]{x1D6FC}}$
under
![]() $vk{\hookrightarrow}w_{\unicode[STIX]{x1D6FC}}K_{\unicode[STIX]{x1D6FC}}$
and, further,
$vk{\hookrightarrow}w_{\unicode[STIX]{x1D6FC}}K_{\unicode[STIX]{x1D6FC}}$
and, further,
![]() $kv=K_{\unicode[STIX]{x1D6FC}}w_{\unicode[STIX]{x1D6FC}}$
is the finite field of cardinality
$kv=K_{\unicode[STIX]{x1D6FC}}w_{\unicode[STIX]{x1D6FC}}$
is the finite field of cardinality
![]() $f_{v}=f_{w_{\unicode[STIX]{x1D6FC}}}$
. One has the following.
$f_{v}=f_{w_{\unicode[STIX]{x1D6FC}}}$
. One has the following.
-
(a)
 $w(b)$
is the minimal positive element of
$w(b)$
is the minimal positive element of
 $w(K^{\times })$
. Indeed, for
$w(K^{\times })$
. Indeed, for
 $t\in \mathfrak{m}_{w}$
, in the above notation one has
$t\in \mathfrak{m}_{w}$
, in the above notation one has
 $w(t)=w_{\unicode[STIX]{x1D6FC}}(t)\geqslant w_{\unicode[STIX]{x1D6FC}}(b)=w(b)$
.
$w(t)=w_{\unicode[STIX]{x1D6FC}}(t)\geqslant w_{\unicode[STIX]{x1D6FC}}(b)=w(b)$
. -
(b)
 $kv=Kw$
and thus
$kv=Kw$
and thus
 $f_{v}=f_{w_{\unicode[STIX]{x1D6FC}}}$
. Indeed, if
$f_{v}=f_{w_{\unicode[STIX]{x1D6FC}}}$
. Indeed, if
 $t\in {\mathcal{O}}_{w}$
, then in the above notation the residue
$t\in {\mathcal{O}}_{w}$
, then in the above notation the residue
 $\overline{t}\in Kw$
satisfies
$\overline{t}\in Kw$
satisfies
 $\overline{t}\in K_{\unicode[STIX]{x1D6FC}}w_{\unicode[STIX]{x1D6FC}}=kv$
.
$\overline{t}\in K_{\unicode[STIX]{x1D6FC}}w_{\unicode[STIX]{x1D6FC}}=kv$
.
Therefore,
![]() $w$
is a
$w$
is a
![]() $p$
-adic valuation of rank
$p$
-adic valuation of rank
![]() $d_{w}=d_{v}$
, which is unique, by the uniqueness of
$d_{w}=d_{v}$
, which is unique, by the uniqueness of
![]() $w_{\unicode[STIX]{x1D6FC}}=w|_{K_{\unicode[STIX]{x1D6FC}}}$
for every subfield
$w_{\unicode[STIX]{x1D6FC}}=w|_{K_{\unicode[STIX]{x1D6FC}}}$
for every subfield
![]() $K_{\unicode[STIX]{x1D6FC}}$
. This concludes the proof of Theorem B.
$K_{\unicode[STIX]{x1D6FC}}$
. This concludes the proof of Theorem B.
4 Proof of the other announced results
(A) Proof of Theorem A
The following stronger assertion holds (from which Theorem A immediately follows).
Theorem 6. Let
![]() $k|\mathbb{Q}_{p}$
be a finite extension containing the
$k|\mathbb{Q}_{p}$
be a finite extension containing the
![]() $p$
th roots of unity, and let
$p$
th roots of unity, and let
![]() $k_{0}\subseteq k$
be a subfield which is relatively algebraically closed in
$k_{0}\subseteq k$
be a subfield which is relatively algebraically closed in
![]() $k$
. Let
$k$
. Let
![]() $X_{0}$
be a complete smooth
$X_{0}$
be a complete smooth
![]() $k_{0}$
-variety, and
$k_{0}$
-variety, and
![]() $K_{0}=k_{0}(X)$
be the function field of
$K_{0}=k_{0}(X)$
be the function field of
![]() $X_{0}$
. The following hold.
$X_{0}$
. The following hold.
-
(1) Every
 $k$
-rational point
$k$
-rational point
 $x\in X_{0}$
gives rise to a bouquet of conjugacy classes of liftable sections
$x\in X_{0}$
gives rise to a bouquet of conjugacy classes of liftable sections
 $s_{x}^{\prime }$
of
$s_{x}^{\prime }$
of
 $\operatorname{Gal}(K_{0}^{\prime }|K_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|k_{0})$
above
$\operatorname{Gal}(K_{0}^{\prime }|K_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|k_{0})$
above
 $x$
.
$x$
. -
(2) Suppose that
 $p>2$
and let
$p>2$
and let
 $s^{\prime }$
be a liftable section of
$s^{\prime }$
be a liftable section of
 $\operatorname{Gal}(K_{0}^{\prime }|K_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|k_{0})$
. Then there exists a unique
$\operatorname{Gal}(K_{0}^{\prime }|K_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|k_{0})$
. Then there exists a unique
 $k$
-rational point
$k$
-rational point
 $x\in X_{0}$
such that
$x\in X_{0}$
such that
 $s^{\prime }$
equals one of the sections
$s^{\prime }$
equals one of the sections
 $s_{x}^{\prime }$
above.
$s_{x}^{\prime }$
above.
Proof. The proof is very similar to the proof of Pop [Reference PopPop10, Theorem A]. We repeat here the arguments briefly for the reader’s sake.
To (1): Let
![]() $v$
be the valuation of
$v$
be the valuation of
![]() $k$
. We notice that by § 2(C)(b), there exists a bijection from the set of (equivalence classes of)
$k$
. We notice that by § 2(C)(b), there exists a bijection from the set of (equivalence classes of)
![]() $p$
-adic valuations
$p$
-adic valuations
![]() $w$
of
$w$
of
![]() $K_{0}=\unicode[STIX]{x1D705}(X_{0})$
with
$K_{0}=\unicode[STIX]{x1D705}(X_{0})$
with
![]() $d_{w}=d_{v}$
onto the set of bouquets of liftable sections above
$d_{w}=d_{v}$
onto the set of bouquets of liftable sections above
![]() $k$
-rational points
$k$
-rational points
![]() $x$
of
$x$
of
![]() $X_{0}$
, which sends each
$X_{0}$
, which sends each
![]() $w$
to the corresponding bouquet of liftable sections above the center
$w$
to the corresponding bouquet of liftable sections above the center
![]() $x$
of the canonical coarsening
$x$
of the canonical coarsening
![]() $w_{1}$
on
$w_{1}$
on
![]() $X=X_{0}\times _{k_{0}}k$
. We conclude by applying assertion (1) of Theorem B.
$X=X_{0}\times _{k_{0}}k$
. We conclude by applying assertion (1) of Theorem B.
To (2): Since
![]() $k_{0}\subseteq k$
is relatively algebraically closed, it follows that
$k_{0}\subseteq k$
is relatively algebraically closed, it follows that
![]() $k_{0}$
is
$k_{0}$
is
![]() $p$
-adically closed. Let
$p$
-adically closed. Let
![]() $v$
be the valuation of
$v$
be the valuation of
![]() $k$
and of all subfields of
$k$
and of all subfields of
![]() $k$
. Since
$k$
. Since
![]() $k_{0}$
is
$k_{0}$
is
![]() $p$
-adically closed, we can apply Theorem B and get: for every liftable section
$p$
-adically closed, we can apply Theorem B and get: for every liftable section
![]() $s^{\prime }$
of
$s^{\prime }$
of
![]() $\operatorname{Gal}(K_{0}^{\prime }|K_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|k_{0})$
, there exists a unique
$\operatorname{Gal}(K_{0}^{\prime }|K_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|k_{0})$
, there exists a unique
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $w$
of
$w$
of
![]() $K_{0}$
which prolongs
$K_{0}$
which prolongs
![]() $v$
to
$v$
to
![]() $K_{0}$
and has
$K_{0}$
and has
![]() $p$
-adic rank equal to the
$p$
-adic rank equal to the
![]() $p$
-adic rank of
$p$
-adic rank of
![]() $v$
, such that
$v$
, such that
![]() $s^{\prime }$
is a section above
$s^{\prime }$
is a section above
![]() $w$
. Let
$w$
. Let
![]() $w_{1}$
be the canonical coarsening of
$w_{1}$
be the canonical coarsening of
![]() $w$
. Then we have the following cases.
$w$
. Then we have the following cases.
Case 1. The valuation
![]() $w_{1}$
is trivial.
$w_{1}$
is trivial.
Then
![]() $w$
is a discrete
$w$
is a discrete
![]() $p$
-adic valuation of
$p$
-adic valuation of
![]() $K$
prolonging
$K$
prolonging
![]() $v$
to
$v$
to
![]() $K$
, having the same residue field and the same value group as
$K$
, having the same residue field and the same value group as
![]() $v$
. Equivalently, the completions of
$v$
. Equivalently, the completions of
![]() $k_{0}$
and
$k_{0}$
and
![]() $K_{0}$
are equal and hence equal to
$K_{0}$
are equal and hence equal to
![]() $k$
. Therefore,
$k$
. Therefore,
![]() $w$
is uniquely determined by the embedding
$w$
is uniquely determined by the embedding
![]() $\imath _{w}:(K_{0},w){\hookrightarrow}(k,v)$
. In geometric terms,
$\imath _{w}:(K_{0},w){\hookrightarrow}(k,v)$
. In geometric terms,
![]() $\imath _{w}$
defines a
$\imath _{w}$
defines a
![]() $k$
-rational point
$k$
-rational point
![]() $x$
of
$x$
of
![]() $X_{0}$
, etc.
$X_{0}$
, etc.
Case 2. The valuation
![]() $w_{1}$
is not trivial.
$w_{1}$
is not trivial.
Then
![]() $w_{1}$
is a
$w_{1}$
is a
![]() $k_{0}$
-rational place of
$k_{0}$
-rational place of
![]() $K_{0}$
and hence defines a
$K_{0}$
and hence defines a
![]() $k_{0}$
-rational point
$k_{0}$
-rational point
![]() $x_{0}$
of
$x_{0}$
of
![]() $X_{0}$
; hence, by base change, a
$X_{0}$
; hence, by base change, a
![]() $k$
-rational point
$k$
-rational point
![]() $x$
of
$x$
of
![]() $X_{0}$
as well, etc.◻
$X_{0}$
as well, etc.◻
(B) Proof of Theorem B0
The proof is almost identical with the one of Theorem B0
from Pop [Reference PopPop10]. The proof of assertion (1) is identical with the proof of assertion (1) of Theorem B; thus, we omit it. Concerning the proof of assertion (2), let
![]() $s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
be a given liftable section of
$s_{L}^{\prime }:\operatorname{Gal}(k^{\prime }|l)\rightarrow \operatorname{Gal}(K^{\prime }|L)$
be a given liftable section of
![]() $\operatorname{pr}_{L}^{\prime }:\operatorname{Gal}(K^{\prime }|L)\rightarrow \operatorname{Gal}(k^{\prime }|l)$
. Then considering the restriction
$\operatorname{pr}_{L}^{\prime }:\operatorname{Gal}(K^{\prime }|L)\rightarrow \operatorname{Gal}(k^{\prime }|l)$
. Then considering the restriction
it follows by mere definitions that
![]() $s^{\prime }$
is a liftable section of
$s^{\prime }$
is a liftable section of
![]() $\operatorname{pr}_{K}^{\prime }:\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(k^{\prime }|k)$
. Hence, by Theorem B, there exists a unique
$\operatorname{pr}_{K}^{\prime }:\operatorname{Gal}(K^{\prime }|K)\rightarrow \operatorname{Gal}(k^{\prime }|k)$
. Hence, by Theorem B, there exists a unique
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $w^{1}$
of
$w^{1}$
of
![]() $K$
which prolongs the
$K$
which prolongs the
![]() $p$
-adic valuation
$p$
-adic valuation
![]() $v_{k}$
of
$v_{k}$
of
![]() $k$
to
$k$
to
![]() $K$
and has
$K$
and has
![]() $d_{w^{1}}=d_{v_{k}}$
, and
$d_{w^{1}}=d_{v_{k}}$
, and
![]() $s^{\prime }=s_{w^{1}}$
in the usual way.
$s^{\prime }=s_{w^{1}}$
in the usual way.
Let
![]() $w=w^{1}|_{L}$
be the restriction of
$w=w^{1}|_{L}$
be the restriction of
![]() $w^{1}$
to
$w^{1}$
to
![]() $L$
. Then
$L$
. Then
![]() $w$
prolongs the valuation
$w$
prolongs the valuation
![]() $v$
of
$v$
of
![]() $l$
to
$l$
to
![]() $L$
. We claim that
$L$
. We claim that
![]() $w^{1}$
is the unique prolongation of
$w^{1}$
is the unique prolongation of
![]() $w$
to
$w$
to
![]() $K$
. Indeed, let
$K$
. Indeed, let
![]() $w^{2}:=w^{1}\circ \unicode[STIX]{x1D70E}_{0}$
, with
$w^{2}:=w^{1}\circ \unicode[STIX]{x1D70E}_{0}$
, with
![]() $\unicode[STIX]{x1D70E}_{0}\in \operatorname{Gal}(k|l)$
, be a further prolongation of
$\unicode[STIX]{x1D70E}_{0}\in \operatorname{Gal}(k|l)$
, be a further prolongation of
![]() $w$
to
$w$
to
![]() $K$
. Then, if
$K$
. Then, if
![]() $(w^{i})^{\prime }$
is a prolongation of
$(w^{i})^{\prime }$
is a prolongation of
![]() $w^{i}$
to
$w^{i}$
to
![]() $K^{\prime }$
,
$K^{\prime }$
,
![]() $i=1,2$
, and
$i=1,2$
, and
![]() $\unicode[STIX]{x1D70E}\in \operatorname{im}(s_{L}^{\prime })$
is a preimage of
$\unicode[STIX]{x1D70E}\in \operatorname{im}(s_{L}^{\prime })$
is a preimage of
![]() $\unicode[STIX]{x1D70E}_{0}$
, then
$\unicode[STIX]{x1D70E}_{0}$
, then
![]() $(w^{2})^{\prime }:=(w^{1})^{\prime }\circ \unicode[STIX]{x1D70E}$
is a prolongation of
$(w^{2})^{\prime }:=(w^{1})^{\prime }\circ \unicode[STIX]{x1D70E}$
is a prolongation of
![]() $w^{2}$
to
$w^{2}$
to
![]() $K^{\prime }$
. Therefore, if
$K^{\prime }$
. Therefore, if
![]() $Z_{w^{1}}\subset \operatorname{Gal}(K^{\prime }|K)$
is the decomposition group above
$Z_{w^{1}}\subset \operatorname{Gal}(K^{\prime }|K)$
is the decomposition group above
![]() $w^{1}$
, then
$w^{1}$
, then
![]() $Z_{w^{2}}:=\unicode[STIX]{x1D70E}Z_{w^{1}}\unicode[STIX]{x1D70E}^{-1}$
is the decomposition group above
$Z_{w^{2}}:=\unicode[STIX]{x1D70E}Z_{w^{1}}\unicode[STIX]{x1D70E}^{-1}$
is the decomposition group above
![]() $w^{2}$
. On the other hand,
$w^{2}$
. On the other hand,
![]() $\operatorname{im}(s^{\prime })\subseteq Z_{w^{1}}$
by Theorem B. Since
$\operatorname{im}(s^{\prime })\subseteq Z_{w^{1}}$
by Theorem B. Since
![]() $\operatorname{Gal}(k^{\prime }|k)$
is a normal subgroup of
$\operatorname{Gal}(k^{\prime }|k)$
is a normal subgroup of
![]() $\operatorname{Gal}(k^{\prime }|l)$
, it follows that
$\operatorname{Gal}(k^{\prime }|l)$
, it follows that
![]() $\operatorname{im}(s^{\prime })$
is normal in
$\operatorname{im}(s^{\prime })$
is normal in
![]() $\operatorname{im}(s_{L}^{\prime })$
. Hence, if
$\operatorname{im}(s_{L}^{\prime })$
. Hence, if
![]() $\unicode[STIX]{x1D70E}\in \operatorname{im}(s_{L}^{\prime })$
, it follows that
$\unicode[STIX]{x1D70E}\in \operatorname{im}(s_{L}^{\prime })$
, it follows that
![]() $\unicode[STIX]{x1D70E}(\operatorname{im}(s^{\prime }))\unicode[STIX]{x1D70E}^{-1}=\operatorname{im}(s^{\prime })$
and, therefore, one has
$\unicode[STIX]{x1D70E}(\operatorname{im}(s^{\prime }))\unicode[STIX]{x1D70E}^{-1}=\operatorname{im}(s^{\prime })$
and, therefore, one has
Hence,
![]() $\operatorname{im}(s^{\prime })\subset Z_{w^{1}},Z_{w^{2}}$
; thus, by the uniqueness assertion of Theorem B, we must have
$\operatorname{im}(s^{\prime })\subset Z_{w^{1}},Z_{w^{2}}$
; thus, by the uniqueness assertion of Theorem B, we must have
![]() $w^{1}=w^{2}$
. Equivalently, if
$w^{1}=w^{2}$
. Equivalently, if
![]() $\unicode[STIX]{x1D70E}\in \operatorname{im}(s_{L}^{\prime })$
, then
$\unicode[STIX]{x1D70E}\in \operatorname{im}(s_{L}^{\prime })$
, then
![]() $\unicode[STIX]{x1D70E}Z_{w^{1}}\unicode[STIX]{x1D70E}^{-1}=Z_{w^{1}}$
and therefore
$\unicode[STIX]{x1D70E}Z_{w^{1}}\unicode[STIX]{x1D70E}^{-1}=Z_{w^{1}}$
and therefore
![]() $\unicode[STIX]{x1D70E}\in Z_{w^{1}}$
. Finally, we conclude that
$\unicode[STIX]{x1D70E}\in Z_{w^{1}}$
. Finally, we conclude that
![]() $d_{w}=d_{v}$
, as claimed, and this concludes the proof of Theorem B0
.
$d_{w}=d_{v}$
, as claimed, and this concludes the proof of Theorem B0
.
(C) Proof of Theorem A0
The following stronger assertion holds (from which Theorem A0 follows immediately).
Theorem 7. Let
![]() $l|\mathbb{Q}_{p}$
be a finite extension. Let
$l|\mathbb{Q}_{p}$
be a finite extension. Let
![]() $l_{0}\subset l$
be a relatively algebraically closed subfield, and
$l_{0}\subset l$
be a relatively algebraically closed subfield, and
![]() $k_{0}|l_{0}$
a finite Galois extension with
$k_{0}|l_{0}$
a finite Galois extension with
![]() $\unicode[STIX]{x1D707}_{p}\subset k_{0}$
. Let
$\unicode[STIX]{x1D707}_{p}\subset k_{0}$
. Let
![]() $Y_{0}$
be a complete smooth geometrically integral variety over
$Y_{0}$
be a complete smooth geometrically integral variety over
![]() $l_{0}$
. Let
$l_{0}$
. Let
![]() $L_{0}=\unicode[STIX]{x1D705}(Y_{0})$
the function field of
$L_{0}=\unicode[STIX]{x1D705}(Y_{0})$
the function field of
![]() $Y_{0}$
, and
$Y_{0}$
, and
![]() $K_{0}=L_{0}k_{0}$
.
$K_{0}=L_{0}k_{0}$
.
-
(1) Every
 $l$
-rational point
$l$
-rational point
 $y\in Y_{0}$
gives rise to a bouquet of conjugacy classes of liftable sections
$y\in Y_{0}$
gives rise to a bouquet of conjugacy classes of liftable sections
 $s_{y}^{\prime }$
of
$s_{y}^{\prime }$
of
 $\operatorname{Gal}(K_{0}^{\prime }|L_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|l_{0})$
above
$\operatorname{Gal}(K_{0}^{\prime }|L_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|l_{0})$
above
 $y$
.
$y$
. -
(2) Let
 $p>2$
and
$p>2$
and
 $s^{\prime }:\operatorname{Gal}(k_{0}^{\prime }|l_{0})\rightarrow \operatorname{Gal}(K_{0}^{\prime }|L_{0})$
be a liftable section of
$s^{\prime }:\operatorname{Gal}(k_{0}^{\prime }|l_{0})\rightarrow \operatorname{Gal}(K_{0}^{\prime }|L_{0})$
be a liftable section of
 $\operatorname{Gal}(K_{0}^{\prime }|L_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|l_{0})$
. Then there exists a unique
$\operatorname{Gal}(K_{0}^{\prime }|L_{0})\rightarrow \operatorname{Gal}(k_{0}^{\prime }|l_{0})$
. Then there exists a unique
 $l$
-rational point
$l$
-rational point
 $y\in Y_{0}(l)$
such that
$y\in Y_{0}(l)$
such that
 $s^{\prime }$
equals one of the sections
$s^{\prime }$
equals one of the sections
 $s_{y}^{\prime }$
introduced in point (1) above.
$s_{y}^{\prime }$
introduced in point (1) above.
Acknowledgements
I would like to thank among others Jordan Ellenberg, Moshe Jarden, Dan Haran, Minhyong Kim, Jochen Koenigsmann, Jakob Stix, Tamás Szamuely, and Adam Topaz for useful discussions concerning the topic and the techniques of this manuscript. Parts of this research were partially performed while visiting MPIM Bonn in May 2012 and HIM Bonn in spring 2013. I would like to thank these institutions for the wonderful research environments and the excellent working conditions.