Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-18T17:43:30.124Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher-order flow modes in turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  16 September 2016

Heng-Dong Xi ,
Yi-Bao Zhang ,
Jian-Tao Hao  and
Ke-Qing Xia
Heng-Dong Xi*
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an, China Department of Physics, The Chinese University of Hong Kong, Hong Kong, China Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China
Yi-Bao Zhang
Affiliation:
School of Aeronautics, Northwestern Polytechnical University, Xi’an, China
Jian-Tao Hao
Affiliation:
Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen, China
Ke-Qing Xia
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Hong Kong, China
*
†Email address for correspondence: hengdongxi@nwpu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We present experimental studies of higher-order modes of the flow in turbulent thermal convection in cells of aspect ratio ($\unicode[STIX]{x1D6E4}$) 1 and 0.5. The working fluid is water with the Prandtl number (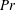$Pr$) kept at around 5.0. The Rayleigh number (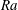$Ra$) ranges from 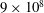$9\times 10^{8}$ to 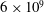$6\times 10^{9}$ for $\unicode[STIX]{x1D6E4}=1$ and from 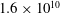$1.6\times 10^{10}$ to 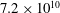$7.2\times 10^{10}$ for 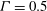$\unicode[STIX]{x1D6E4}=0.5$. We found that in $\unicode[STIX]{x1D6E4}=1$ cells, the first mode, which corresponds to the large-scale circulation (LSC), dominates the flow. The second mode (quadrupole mode), the third mode (sextupole mode) and the fourth mode (octupole mode) are very weak, on average these higher-order modes each contains less than 4 % of the total flow energy. In 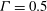$\unicode[STIX]{x1D6E4}=0.5$ cells, the first mode is still the strongest but less dominant, the second mode becomes stronger which contains 13.7 % of the total flow energy and the third and the fourth modes are also stronger (containing 6.5 % and 1.1 % of the total flow energy respectively). It is found that during a reversal/cessation, the amplitude of the second mode and the remaining modes experiences a rapid increase followed by a decrease, which is opposite to the behaviour of the amplitude of the first mode – it decreases to almost zero then rebounds. In addition, it is found that during the cessation (reversal) of the LSC, the second mode dominates, containing 51.3 % (50.1 %) of the total flow energy, which reveals that the commonly called cessation event is not the cessation of the entire flow but only the cessation of the first mode (LSC). The experiment reveals that the second mode and the remaining higher-order modes play important roles in the dynamical process of the reversal/cessation of the LSC. We also show direct evidence that the first mode is more efficient for heat transfer. Furthermore, our study reveals that, during the cessation/reversal of the LSC, 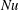$Nu$ drops to its local minimum and the minimum of 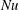$Nu$ is ahead of the minimum of the amplitude of the LSC; and reversals can be distinguished from cessations in terms of global heat transport. A direct velocity measurement reveals the flow structure of the first- and higher-order modes.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 805 , 25 October 2016 , pp. 31 - 51
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Araujo, F. F., Grossmann, S. & Lohse, D. 2005 Wind reversals in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084502.Google Scholar
Benzi, R. 2005 Flow reversal in a simple dynamical model of turbulence. Phys. Rev. Lett. 95, 024502.Google Scholar
Brown, E. & Ahlers, G. 2006a Effect of the Earth’s coriolis force on the large-scale circulation of turbulent Rayleigh–Bénard convection. Phys. Fluids 18, 125108.CrossRefGoogle Scholar
Brown, E. & Ahlers, G. 2006b Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.Google Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.Google Scholar
Brown, E. & Ahlers, G. 2009 The origin of oscillations of the large-scale circulation of turbulent Rayleigh–Bénard convection. J. Fluid Mech. 638, 383–400.CrossRefGoogle Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.Google Scholar
Busse, F. H. 1994 Convection-driven zonal flows and vortices in the major planets. Chaos 4, 123–134.CrossRefGoogle ScholarPubMed
Chandra, M. & Verma, M. K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83 (6).Google Scholar
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110 (11).CrossRefGoogle ScholarPubMed
Chillà, F., Rastello, M., Chaumat, S. & Castaing, B. 2004 Long relaxation times and tilt sensitivity in Rayleigh–Bénard turbulence. Eur. Phys. J. B 40, 223–227.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid. Mech. 335, 111–140.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.Google Scholar
Glatzmaier, G. A., Coe, R. S., Hongre, L. & Roberts, P. H. 1999 The role of the Earth’s mantle in controlling the frequency of geomagnetic reversals. Nature 401, 885–890.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement-induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.Google Scholar
Huang, S.-D. & Xia, K.-Q. 2016 Effects of geometric confinement in quasi-2-D turbulent Rayleigh–Bénard convection. J. Fluid Mech. 794, 639–654.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2008 Breakdown of large-scale circulaiton in turbulent rotating convection. Eur. Phys. Lett. 84, 24001.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Mishra, P. K., De, A. K., Verma, M. K. & Eswaran, V. 2011 Dynamics of reorientaiton and reveral of large-scale-flow in Rayleigh–Bénard convection. J. Fluid. Mech 668, 480–499.Google Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2015 Reversals of the large-scale circulation in quasi-2D Rayleigh–Bénard convection. J. Fluid Mech. 778, R5.CrossRefGoogle Scholar
Nikolaenko, A., Brown, E., Funfschilling, D. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and less. J. Fluid Mech. 523, 251–260.Google Scholar
Podvin, B. & Sergent, A. 2015 A large-scale investigation of wind reversal in a square Rayleigh–Bénard cell. J. Fluid Mech. 766, 172–201.CrossRefGoogle Scholar
Roche, P. E., Castaing, B., Chabaud, B. & Hebral, B. 2002 Prandtl and Rayleigh numbers dependences in Rayleigh–Bénard convection. Eur. Phys. Lett. 58, 693–698.Google Scholar
Sreenivasan, K. R., Bershadskii, A. & Niemela, J. J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65, 056306.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2011 Effect of plumes on measuring the large scale circulation in turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 095110.CrossRefGoogle Scholar
Stringano, G. & Verzicco, R. 2006 Mean flow structure in thermal convection in a cylindrical cell of aspect ratio one half. J. Fluid. Mech 548, 1–16.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.Google Scholar
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005a Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.CrossRefGoogle Scholar
Sun, C., Xia, K.-Q. & Tong, P. 2005b Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72, 026302.Google Scholar
Verma, M. K., Ambhire, S. C. & Pandey, A. 2015 Flow reversals in turbulent convection with free-slip walls. Phys. Fluids 27 (4), 047102.Google Scholar
Weiss, S. & Ahlers, G. 2011a The large scale flow structure in turbulent rotating Rayleigh–Bénard convection. J. Fluid Mech. 688, 461–492.Google Scholar
Weiss, S. & Ahlers, G. 2011b Turbulent Rayleigh–Bénard convection in a cylindrical container with aspect ratio 𝛤 = 0. 50 and Prandtl number Pr = 4. 38. J. Fluid Mech. 676, 5–40.Google Scholar
Weiss, S. & Ahlers, G. 2013 Effect of tilting on turbulent convection: cylindrical samples with aspect ratio 𝛤 = 0. 50. J. Fluid Mech. 715, 314–334.Google Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid. Mech 503, 47–56.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2007 The cessations and reversals of the large-scale circulation in turbulent thermal convection. Phys. Rev. E 75, 066307.Google ScholarPubMed
Xi, H.-D. & Xia, K.-Q. 2008a Azimuthal motion, reorientation, cessation and reversal of the large-scale circulation in turbulent thermal convection: a comparative study in aspect ratio one and one-half geometries. Phys. Rev. E 78, 036326.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008b Flow mode transition in turbulent thermal convection. Phys. Fluids 20, 055104.Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.Google Scholar
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.Google Scholar
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3, 052001.Google Scholar
Zhou, Q., Xi, H.-D., Zhou, S. Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid. Mech 630, 367–390.Google Scholar