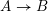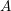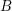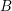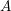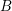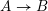Notations. If
![]() $A$
is a local ring, we denote by
$A$
is a local ring, we denote by
![]() $\mathfrak{m}_{A}$
its maximal ideal and by
$\mathfrak{m}_{A}$
its maximal ideal and by
![]() $\unicode[STIX]{x1D705}(A)$
its residue field. The embedding dimension of
$\unicode[STIX]{x1D705}(A)$
its residue field. The embedding dimension of
![]() $A$
, i.e. the minimal number of generators of
$A$
, i.e. the minimal number of generators of
![]() $\mathfrak{m}_{A}$
, is denoted by
$\mathfrak{m}_{A}$
, is denoted by
![]() $\operatorname{edim}(A)$
. A local morphism
$\operatorname{edim}(A)$
. A local morphism
![]() $A\rightarrow B$
of Noetherian local rings is a relative complete intersection if the ring
$A\rightarrow B$
of Noetherian local rings is a relative complete intersection if the ring
![]() $B/\mathfrak{m}_{A}B$
is a complete intersection.
$B/\mathfrak{m}_{A}B$
is a complete intersection.
1 Introduction
A crucial step in the proof of the modularity of semistable elliptic curves over
![]() $\mathbb{Q}$
by Taylor and Wiles is to show that certain Hecke algebras are complete intersections. Their method, now commonly referred to as a ‘patching method’, heuristically consists of considering the limit of algebras arising from forms of different levels. In their construction, they used in particular the following (fundamental) ‘multiplicity one’ result: the homology of the modular curve is a free module over the Hecke algebra (after localization at some maximal ideal). Diamond reversed the argument in [Reference DiamondDia97]: ‘multiplicity one’ becomes a byproduct of the proof rather than an ingredient. The key input from commutative algebra that allowed Diamond’s improvement was the freeness criterion [Reference DiamondDia97, Theorem 2.1]. Its proof still relies on a patching argument.
$\mathbb{Q}$
by Taylor and Wiles is to show that certain Hecke algebras are complete intersections. Their method, now commonly referred to as a ‘patching method’, heuristically consists of considering the limit of algebras arising from forms of different levels. In their construction, they used in particular the following (fundamental) ‘multiplicity one’ result: the homology of the modular curve is a free module over the Hecke algebra (after localization at some maximal ideal). Diamond reversed the argument in [Reference DiamondDia97]: ‘multiplicity one’ becomes a byproduct of the proof rather than an ingredient. The key input from commutative algebra that allowed Diamond’s improvement was the freeness criterion [Reference DiamondDia97, Theorem 2.1]. Its proof still relies on a patching argument.
In the hypotheses of Diamond’s freeness criterion, there is a condition that has to hold for all positive integers
![]() $n$
. The condition for
$n$
. The condition for
![]() $n$
implies the condition for all smaller integers. In [Reference DiamondDia97, Remark 2.2], Diamond asks whether a sufficiently large
$n$
implies the condition for all smaller integers. In [Reference DiamondDia97, Remark 2.2], Diamond asks whether a sufficiently large
![]() $n$
would be enough, and whether there could exist a lower bound for such an
$n$
would be enough, and whether there could exist a lower bound for such an
![]() $n$
depending only on the number
$n$
depending only on the number
![]() $r$
of variables and the rank of the module. Around 1997, de Smit conjectured that if
$r$
of variables and the rank of the module. Around 1997, de Smit conjectured that if
![]() $A\rightarrow B$
is a morphism of Artin local rings with the same embedding dimension, then any
$A\rightarrow B$
is a morphism of Artin local rings with the same embedding dimension, then any
![]() $A$
-flat
$A$
-flat
![]() $B$
-module is
$B$
-module is
![]() $B$
-flat (see Corollary 1.2 below). In [Reference Brochard and MézardBM11] we proved de Smit’s conjecture when the embedding dimension
$B$
-flat (see Corollary 1.2 below). In [Reference Brochard and MézardBM11] we proved de Smit’s conjecture when the embedding dimension
![]() $r$
is
$r$
is
![]() ${\leqslant}2$
, and with the additional assumption that
${\leqslant}2$
, and with the additional assumption that
![]() $A\rightarrow B$
was flat. Here we prove the following theorem, which in particular proves the full conjecture, and answers Diamond’s question:
$A\rightarrow B$
was flat. Here we prove the following theorem, which in particular proves the full conjecture, and answers Diamond’s question:
![]() $n=2$
already suffices, for any
$n=2$
already suffices, for any
![]() $r$
and any module. So, the freeness criterion will be much easier to apply.
$r$
and any module. So, the freeness criterion will be much easier to apply.
Theorem 1.1. Let
![]() $\unicode[STIX]{x1D711}:A\rightarrow B$
be a local morphism of Noetherian local rings. Assume the following:
$\unicode[STIX]{x1D711}:A\rightarrow B$
be a local morphism of Noetherian local rings. Assume the following:
-
(i)
 $\operatorname{edim}(B)\leqslant \operatorname{edim}(A)$
;
$\operatorname{edim}(B)\leqslant \operatorname{edim}(A)$
; -
(ii) there is a nonzero
 $A$
-flat
$A$
-flat
 $B$
-module
$B$
-module
 $M$
;
$M$
; -
(iii)
 $A$
and
$A$
and
 $B$
are Artin or
$B$
are Artin or
 $M$
is of finite type as a
$M$
is of finite type as a
 $B$
-module.
$B$
-module.
Then:
-
(1) the morphism
 $A\rightarrow B$
is flat and
$A\rightarrow B$
is flat and
 $\operatorname{edim}(B)=\operatorname{edim}(A)$
;
$\operatorname{edim}(B)=\operatorname{edim}(A)$
; -
(2) the ring
 $B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero;
$B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero; -
(3)
 $M$
is flat over
$M$
is flat over
 $B$
.
$B$
.
Corollary 1.2 (de Smit’s conjecture).
Let
![]() $A\rightarrow B$
be a morphism of Artin local rings with the same embedding dimension. Then any
$A\rightarrow B$
be a morphism of Artin local rings with the same embedding dimension. Then any
![]() $A$
-flat
$A$
-flat
![]() $B$
-module is
$B$
-module is
![]() $B$
-flat.
$B$
-flat.
Corollary 1.3 (see Theorem 2.5).
Let
![]() $f:X\rightarrow S$
be a morphism of locally Noetherian schemes such that for any
$f:X\rightarrow S$
be a morphism of locally Noetherian schemes such that for any
![]() $x\in X$
, the tangent spaces satisfy
$x\in X$
, the tangent spaces satisfy
![]() $\dim T_{x}\leqslant \dim T_{f(x)}$
. Then any
$\dim T_{x}\leqslant \dim T_{f(x)}$
. Then any
![]() $S$
-flat coherent
$S$
-flat coherent
![]() ${\mathcal{O}}_{X}$
-module is also flat over
${\mathcal{O}}_{X}$
-module is also flat over
![]() $X$
.
$X$
.
Since its publication, Diamond’s freeness criterion and the related patching method have been used quite a lot. For instance, here is a list of papers (nonexhaustive, in chronological order) that directly use Diamond’s Theorem 2.1: [Reference Conrad, Diamond and TaylorCDT99, Reference DickinsonDic01, Reference Genestier and TilouineGT05, Reference Böckle and KhareBK06, Reference TaylorTay06, Reference Clozel, Harris and TaylorCHT08, Reference DimitrovDim09, Reference PilloniPil12, Reference HarrisHar13, Reference Breuil and DiamondBD14]. A variant of this freeness criterion, due to Kisin (see [Reference KisinKis09c, (3.3.1)]), was also used in several major results, for instance the proof of Serre’s modularity conjecture (see [Reference KisinKis09c, Reference Khare and WintenbergerKW09, Reference KisinKis09b]) or the Fontaine–Mazur conjecture for
![]() $\operatorname{GL}_{2}$
(see [Reference KisinKis09a]). A more functorial approach of the patching method is proposed in [Reference Emerton, Gee and SavittEGS15].
$\operatorname{GL}_{2}$
(see [Reference KisinKis09a]). A more functorial approach of the patching method is proposed in [Reference Emerton, Gee and SavittEGS15].
The paper is organized as follows: in § 2 we prove Theorem 1.1. We also give a global version for schemes that are not necessarily local (see Theorem 2.5). In § 3 we briefly explain how this new freeness criterion allows us to simplify Wiles’s proof of Fermat’s last theorem and avoid the use of the patching method.
2 Proof of Theorem 1.1
The following lemma is the heart of the proof.
Lemma 2.1. Let
![]() $B$
be a ring. Let
$B$
be a ring. Let
![]() $(x_{1},\ldots ,x_{n})$
and
$(x_{1},\ldots ,x_{n})$
and
![]() $(u_{1},\ldots ,u_{n})$
be sequences of elements of
$(u_{1},\ldots ,u_{n})$
be sequences of elements of
![]() $B$
and let us denote by
$B$
and let us denote by
![]() $J_{x}$
and
$J_{x}$
and
![]() $J_{u}$
the ideals they generate. Let
$J_{u}$
the ideals they generate. Let
![]() $M$
be a
$M$
be a
![]() $B$
-module. Assume that:
$B$
-module. Assume that:
-
(i) we have the inclusion of ideals
 $J_{x}\subset J_{u}$
, in other words, if
$J_{x}\subset J_{u}$
, in other words, if
 $x$
and
$x$
and
 $u$
denote the column matrices
$u$
denote the column matrices
 $(x_{1},\ldots ,x_{n})^{T}$
and
$(x_{1},\ldots ,x_{n})^{T}$
and
 $(u_{1},\ldots ,u_{n})^{T}$
, there is a square
$(u_{1},\ldots ,u_{n})^{T}$
, there is a square
 $n\times n$
matrix
$n\times n$
matrix
 $W=(c_{ij})$
with entries in
$W=(c_{ij})$
with entries in
 $B$
such that
$B$
such that
 $x=Wu$
. Let
$x=Wu$
. Let
 $\unicode[STIX]{x1D6E5}=\det W$
;
$\unicode[STIX]{x1D6E5}=\det W$
; -
(ii) for any
 $m_{1},\ldots ,m_{n}\in M$
, if we have the relation
$m_{1},\ldots ,m_{n}\in M$
, if we have the relation
 $\sum _{i=1}^{n}x_{i}m_{i}=0$
, then
$\sum _{i=1}^{n}x_{i}m_{i}=0$
, then
 $m_{i}\in J_{x}M$
for all
$m_{i}\in J_{x}M$
for all
 $i$
.
$i$
.
Then, for any
![]() $m\in M$
, if
$m\in M$
, if
![]() $\unicode[STIX]{x1D6E5}m\in J_{x}M$
, then
$\unicode[STIX]{x1D6E5}m\in J_{x}M$
, then
![]() $m\in J_{u}M$
.
$m\in J_{u}M$
.
Proof. We will need some notations for the minors of
![]() $W$
. For any integer
$W$
. For any integer
![]() $\ell$
, let
$\ell$
, let
![]() $E_{\ell }$
be the set
$E_{\ell }$
be the set
![]() $\{1,\ldots ,\ell \}$
and let
$\{1,\ldots ,\ell \}$
and let
![]() ${\mathcal{P}}_{\ell }$
be the set of subsets
${\mathcal{P}}_{\ell }$
be the set of subsets
![]() $I\subset E_{n}$
such that
$I\subset E_{n}$
such that
![]() $|I|=\ell$
. For
$|I|=\ell$
. For
![]() $I,J\in {\mathcal{P}}_{\ell }$
, let
$I,J\in {\mathcal{P}}_{\ell }$
, let
![]() $\unicode[STIX]{x1D6E5}_{J}^{I}$
denote the minor of
$\unicode[STIX]{x1D6E5}_{J}^{I}$
denote the minor of
![]() $W$
obtained by deleting the rows (respectively the columns) whose index is in
$W$
obtained by deleting the rows (respectively the columns) whose index is in
![]() $I$
(respectively
$I$
(respectively
![]() $J$
). In other words,
$J$
). In other words,
![]() $\unicode[STIX]{x1D6E5}_{J}^{I}=\det (c_{ij})_{\substack{ i\in E_{n}\smallsetminus I \\ j\in E_{n}\smallsetminus J}}$
. In particular,
$\unicode[STIX]{x1D6E5}_{J}^{I}=\det (c_{ij})_{\substack{ i\in E_{n}\smallsetminus I \\ j\in E_{n}\smallsetminus J}}$
. In particular,
![]() $\unicode[STIX]{x1D6E5}_{\varnothing }^{\varnothing }=\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}_{\varnothing }^{\varnothing }=\unicode[STIX]{x1D6E5}$
and
![]() $\unicode[STIX]{x1D6E5}_{E_{n}}^{E_{n}}=1$
. The comatrix is
$\unicode[STIX]{x1D6E5}_{E_{n}}^{E_{n}}=1$
. The comatrix is
![]() $\operatorname{Com}(W)=((-1)^{i+j}\unicode[STIX]{x1D6E5}_{j}^{i})$
. If
$\operatorname{Com}(W)=((-1)^{i+j}\unicode[STIX]{x1D6E5}_{j}^{i})$
. If
![]() $I\subset E_{n}$
and
$I\subset E_{n}$
and
![]() $i\in E_{n}$
, we write
$i\in E_{n}$
, we write
![]() $I-i$
for
$I-i$
for
![]() $I\smallsetminus \{i\}$
. For
$I\smallsetminus \{i\}$
. For
![]() $i\neq j\in E_{n}$
, let
$i\neq j\in E_{n}$
, let
![]() $\overline{\unicode[STIX]{x1D700}}(i,j)=1$
if
$\overline{\unicode[STIX]{x1D700}}(i,j)=1$
if
![]() $i<j$
and
$i<j$
and
![]() $\overline{\unicode[STIX]{x1D700}}(i,j)=-1$
if
$\overline{\unicode[STIX]{x1D700}}(i,j)=-1$
if
![]() $i>j$
. For
$i>j$
. For
![]() $I\subset E_{n}$
and
$I\subset E_{n}$
and
![]() $i\in I$
, let
$i\in I$
, let
![]() $\unicode[STIX]{x1D700}(i,I)=(-1)^{p}$
, where
$\unicode[STIX]{x1D700}(i,I)=(-1)^{p}$
, where
![]() $p$
is the position of
$p$
is the position of
![]() $i$
in the ordered set
$i$
in the ordered set
![]() $E_{n}\smallsetminus (I-i)$
. Note that
$E_{n}\smallsetminus (I-i)$
. Note that
![]() $\unicode[STIX]{x1D700}(i,I)=(-1)^{i}\prod _{j\in I-i}\overline{\unicode[STIX]{x1D700}}(i,j)$
. For any
$\unicode[STIX]{x1D700}(i,I)=(-1)^{i}\prod _{j\in I-i}\overline{\unicode[STIX]{x1D700}}(i,j)$
. For any
![]() $i,j\in I$
with
$i,j\in I$
with
![]() $i\neq j$
, we have the relation
$i\neq j$
, we have the relation
Now, for any
![]() $0\leqslant \ell \leqslant n-1$
, if
$0\leqslant \ell \leqslant n-1$
, if
![]() $I\in {\mathcal{P}}_{\ell +1}$
and
$I\in {\mathcal{P}}_{\ell +1}$
and
![]() $i\in I$
, the expansion of the minor
$i\in I$
, the expansion of the minor
![]() $\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}$
along the column
$\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}$
along the column
![]() $i$
is
$i$
is
If
![]() $i\notin I$
, pick an element
$i\notin I$
, pick an element
![]() $j\in I$
and consider the expansion along the column
$j\in I$
and consider the expansion along the column
![]() $j$
of the minor
$j$
of the minor
![]() $\unicode[STIX]{x1D6E5}_{I-j}^{E_{\ell }}$
in which we have replaced the column
$\unicode[STIX]{x1D6E5}_{I-j}^{E_{\ell }}$
in which we have replaced the column
![]() $j$
by the column
$j$
by the column
![]() $i$
. Since the latter minor has two identical columns, it is zero and we see that for any
$i$
. Since the latter minor has two identical columns, it is zero and we see that for any
![]() $i\notin I$
,
$i\notin I$
,
Now let us come back to our module
![]() $M$
. Let
$M$
. Let
![]() $m\in M$
be such that
$m\in M$
be such that
![]() $\unicode[STIX]{x1D6E5}m\in J_{x}M$
. For
$\unicode[STIX]{x1D6E5}m\in J_{x}M$
. For
![]() $0\leqslant \ell \leqslant n$
, let
$0\leqslant \ell \leqslant n$
, let
![]() $(A_{\ell })$
denote the following statement.
$(A_{\ell })$
denote the following statement.
-
 $(A_{\ell })$
$(A_{\ell })$
-
There is a family
 $(a_{I}^{\ell })_{I\in {\mathcal{P}}_{\ell -1}}$
of elements of
$(a_{I}^{\ell })_{I\in {\mathcal{P}}_{\ell -1}}$
of elements of
 $M$
such that for any
$M$
such that for any
 $I\in {\mathcal{P}}_{\ell }$
, the element
$I\in {\mathcal{P}}_{\ell }$
, the element  $$\begin{eqnarray}g_{I}=\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }}m+\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}a_{I-i}^{\ell }\end{eqnarray}$$
$$\begin{eqnarray}g_{I}=\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }}m+\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}a_{I-i}^{\ell }\end{eqnarray}$$
belongs to
 $J_{x}M$
.
$J_{x}M$
.
We will prove that
![]() $(A_{\ell })$
holds for any
$(A_{\ell })$
holds for any
![]() $0\leqslant \ell \leqslant n$
by induction on
$0\leqslant \ell \leqslant n$
by induction on
![]() $\ell$
. The statement
$\ell$
. The statement
![]() $(A_{0})$
means that
$(A_{0})$
means that
![]() $\unicode[STIX]{x1D6E5}m\in J_{x}M$
and holds by assumption. Assume that
$\unicode[STIX]{x1D6E5}m\in J_{x}M$
and holds by assumption. Assume that
![]() $(A_{\ell })$
holds for some
$(A_{\ell })$
holds for some
![]() $0\leqslant \ell \leqslant n-1$
and let us prove the statement
$0\leqslant \ell \leqslant n-1$
and let us prove the statement
![]() $(A_{\ell +1})$
. For any
$(A_{\ell +1})$
. For any
![]() $I\in {\mathcal{P}}_{\ell }$
, since
$I\in {\mathcal{P}}_{\ell }$
, since
![]() $g_{I}\in J_{x}M$
, we can write
$g_{I}\in J_{x}M$
, we can write
![]() $g_{I}=\sum _{k\in E_{n}}x_{k}a_{I}^{k}$
for some elements
$g_{I}=\sum _{k\in E_{n}}x_{k}a_{I}^{k}$
for some elements
![]() $a_{I}^{k}\in M$
. Let
$a_{I}^{k}\in M$
. Let
![]() $I\in {\mathcal{P}}_{\ell +1}$
. We will compute
$I\in {\mathcal{P}}_{\ell +1}$
. We will compute
![]() $m^{\prime }=\sum _{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}g_{I-i}$
. For this, we first compute
$m^{\prime }=\sum _{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}g_{I-i}$
. For this, we first compute
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}(g_{I-i}-\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}m) & = & \displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}\mathop{\sum }_{j\in I-i}\unicode[STIX]{x1D700}(j,I-i)u_{j}a_{I\smallsetminus \{i,j\}}^{\ell }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ i,j\in I \\ i\neq j}}u_{i}u_{j}a_{I\smallsetminus \{i,j\}}^{\ell }S(i,j),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}(g_{I-i}-\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}m) & = & \displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}\mathop{\sum }_{j\in I-i}\unicode[STIX]{x1D700}(j,I-i)u_{j}a_{I\smallsetminus \{i,j\}}^{\ell }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ i,j\in I \\ i\neq j}}u_{i}u_{j}a_{I\smallsetminus \{i,j\}}^{\ell }S(i,j),\nonumber\end{eqnarray}$$
where
![]() $S(i,j)=\unicode[STIX]{x1D700}(i,I)\unicode[STIX]{x1D700}(j,I-i)$
. Now the sum vanishes because
$S(i,j)=\unicode[STIX]{x1D700}(i,I)\unicode[STIX]{x1D700}(j,I-i)$
. Now the sum vanishes because
![]() $S(i,j)=-S(j,i)$
. Indeed,
$S(i,j)=-S(j,i)$
. Indeed,
![]() $S(i,j)S(j,i)=\overline{\unicode[STIX]{x1D700}}(i,j)\overline{\unicode[STIX]{x1D700}}(j,i)$
by (1) above. Hence,
$S(i,j)S(j,i)=\overline{\unicode[STIX]{x1D700}}(i,j)\overline{\unicode[STIX]{x1D700}}(j,i)$
by (1) above. Hence,
We expand
![]() $\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}$
along the column
$\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}$
along the column
![]() $i$
:
$i$
:
 $$\begin{eqnarray}\displaystyle m^{\prime } & = & \displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}(-1)^{\ell }\unicode[STIX]{x1D700}(i,I)\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}c_{ki}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}m\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}\biggl(\mathop{\sum }_{i\in I}c_{ki}u_{i}\biggr)m\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}\biggl(x_{k}-\mathop{\sum }_{i\notin I}c_{ki}u_{i}\biggr)m\quad (\text{because}~x=Wu)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}x_{k}m\quad (\text{using}~(3)~\text{for each}~i\notin I).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle m^{\prime } & = & \displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}(-1)^{\ell }\unicode[STIX]{x1D700}(i,I)\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}c_{ki}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}m\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}\biggl(\mathop{\sum }_{i\in I}c_{ki}u_{i}\biggr)m\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}\biggl(x_{k}-\mathop{\sum }_{i\notin I}c_{ki}u_{i}\biggr)m\quad (\text{because}~x=Wu)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}x_{k}m\quad (\text{using}~(3)~\text{for each}~i\notin I).\nonumber\end{eqnarray}$$
On the other hand, by definition
Hence,
By our assumption (ii), the coefficient of
![]() $x_{\ell +1}$
in the above equation belongs to
$x_{\ell +1}$
in the above equation belongs to
![]() $J_{x}M$
. But this coefficient is
$J_{x}M$
. But this coefficient is
This proves the statement
![]() $(A_{\ell +1})$
. In particular,
$(A_{\ell +1})$
. In particular,
![]() $(A_{n})$
holds and hence there are elements
$(A_{n})$
holds and hence there are elements
![]() $a_{I}^{n}\in M$
for
$a_{I}^{n}\in M$
for
![]() $I\in {\mathcal{P}}_{n-1}$
such that the element
$I\in {\mathcal{P}}_{n-1}$
such that the element
belongs to
![]() $J_{x}M$
. Since
$J_{x}M$
. Since
![]() $\unicode[STIX]{x1D6E5}_{E_{n}}^{E_{n}}=1$
, this proves that
$\unicode[STIX]{x1D6E5}_{E_{n}}^{E_{n}}=1$
, this proves that
![]() $m\in J_{u}M$
.◻
$m\in J_{u}M$
.◻
Before proceeding to the proof of Theorem 1.1, let us recall a result from [Reference Brochard and MézardBM11]. It will provide a useful characterization for the flatness of
![]() $M$
over
$M$
over
![]() $B$
.
$B$
.
Definition 2.2 [Reference Brochard and MézardBM11, 3.1].
Let
![]() $R$
be a local ring and
$R$
be a local ring and
![]() $M$
be an
$M$
be an
![]() $R$
-module. We say that
$R$
-module. We say that
![]() $M$
is weakly torsion-free if, for every
$M$
is weakly torsion-free if, for every
![]() $\unicode[STIX]{x1D706}\in R$
and every
$\unicode[STIX]{x1D706}\in R$
and every
![]() $m\in M$
, the relation
$m\in M$
, the relation
![]() $\unicode[STIX]{x1D706}m=0$
implies that
$\unicode[STIX]{x1D706}m=0$
implies that
![]() $\unicode[STIX]{x1D706}=0$
or
$\unicode[STIX]{x1D706}=0$
or
![]() $m\in \mathfrak{m}_{R}M$
.
$m\in \mathfrak{m}_{R}M$
.
Proposition 2.3 [Reference Brochard and MézardBM11, 3.7].
Let
![]() $R$
be an Artin local ring. Assume that
$R$
be an Artin local ring. Assume that
![]() $R$
is Gorenstein and contains a field. Then an
$R$
is Gorenstein and contains a field. Then an
![]() $R$
-module
$R$
-module
![]() $M$
is flat over
$M$
is flat over
![]() $R$
if and only if it is weakly torsion-free.
$R$
if and only if it is weakly torsion-free.
Proof of Theorem 1.1.
Let
![]() $M$
be a nonzero
$M$
be a nonzero
![]() $A$
-flat
$A$
-flat
![]() $B$
-module. We apply Lemma 2.1 with
$B$
-module. We apply Lemma 2.1 with
![]() $(x_{1},\ldots ,x_{n})$
the image in
$(x_{1},\ldots ,x_{n})$
the image in
![]() $B$
of a minimal system of generators of
$B$
of a minimal system of generators of
![]() $\mathfrak{m}_{A}$
, and
$\mathfrak{m}_{A}$
, and
![]() $(u_{1},\ldots ,u_{n})$
a system of generators of
$(u_{1},\ldots ,u_{n})$
a system of generators of
![]() $\mathfrak{m}_{B}$
, so that
$\mathfrak{m}_{B}$
, so that
![]() $J_{x}=\mathfrak{m}_{A}B$
and
$J_{x}=\mathfrak{m}_{A}B$
and
![]() $J_{u}=\mathfrak{m}_{B}$
. The assumption (i) holds because the morphism
$J_{u}=\mathfrak{m}_{B}$
. The assumption (i) holds because the morphism
![]() $A\rightarrow B$
is local, and the assumption (ii) holds by [Reference Brochard and MézardBM11, 4.2 and 4.3] because
$A\rightarrow B$
is local, and the assumption (ii) holds by [Reference Brochard and MézardBM11, 4.2 and 4.3] because
![]() $M$
is flat over
$M$
is flat over
![]() $A$
. Then
$A$
. Then
![]() $\unicode[STIX]{x1D6E5}\notin \mathfrak{m}_{A}B$
, otherwise we would have
$\unicode[STIX]{x1D6E5}\notin \mathfrak{m}_{A}B$
, otherwise we would have
![]() $\unicode[STIX]{x1D6E5}M\subset \mathfrak{m}_{A}M$
, which would imply that
$\unicode[STIX]{x1D6E5}M\subset \mathfrak{m}_{A}M$
, which would imply that
![]() $M=\mathfrak{m}_{B}M$
by Lemma 2.1; hence,
$M=\mathfrak{m}_{B}M$
by Lemma 2.1; hence,
![]() $M=0$
, which is a contradiction. In particular, for any choice of the matrix
$M=0$
, which is a contradiction. In particular, for any choice of the matrix
![]() $W$
and the generators
$W$
and the generators
![]() $u_{1},\ldots ,u_{n}$
of
$u_{1},\ldots ,u_{n}$
of
![]() $\mathfrak{m}_{B}$
such that
$\mathfrak{m}_{B}$
such that
![]() $x=Wu$
, we have
$x=Wu$
, we have
![]() $\det W\neq 0$
. This proves that
$\det W\neq 0$
. This proves that
![]() $\operatorname{edim}(B)=\operatorname{edim}(A)$
, because if
$\operatorname{edim}(B)=\operatorname{edim}(A)$
, because if
![]() $\operatorname{edim}(B)<\operatorname{edim}(A)$
we can choose
$\operatorname{edim}(B)<\operatorname{edim}(A)$
we can choose
![]() $W$
with a zero column. Moreover, in the ring
$W$
with a zero column. Moreover, in the ring
![]() $B/\mathfrak{m}_{A}B$
, the matrix
$B/\mathfrak{m}_{A}B$
, the matrix
![]() $\overline{W}$
satisfies
$\overline{W}$
satisfies
![]() $\overline{W}u=0$
and
$\overline{W}u=0$
and
![]() $\det \overline{W}\neq 0$
. In the language of [Reference Simon and StrookerSS06, Definition 2.6], this means that
$\det \overline{W}\neq 0$
. In the language of [Reference Simon and StrookerSS06, Definition 2.6], this means that
![]() $\overline{W}$
is (the transpose of) a
$\overline{W}$
is (the transpose of) a
![]() $u$
-Wiebe matrix for the ring
$u$
-Wiebe matrix for the ring
![]() $B/\mathfrak{m}_{A}B$
. By [Reference Simon and StrookerSS06, 2.7], this implies that the ring
$B/\mathfrak{m}_{A}B$
. By [Reference Simon and StrookerSS06, 2.7], this implies that the ring
![]() $B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero, and proves (2).
$B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero, and proves (2).
Let us prove that
![]() $M$
is
$M$
is
![]() $B$
-flat. By [Reference Brochard and MézardBM11, 2.3], it suffices to prove that
$B$
-flat. By [Reference Brochard and MézardBM11, 2.3], it suffices to prove that
![]() $M/\mathfrak{m}_{A}M$
is flat over
$M/\mathfrak{m}_{A}M$
is flat over
![]() $B/\mathfrak{m}_{A}B$
. We have seen that
$B/\mathfrak{m}_{A}B$
. We have seen that
![]() $B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero and hence a Gorenstein Artin local ring. Moreover, it contains the field
$B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero and hence a Gorenstein Artin local ring. Moreover, it contains the field
![]() $\unicode[STIX]{x1D705}(A)$
. Hence, by Proposition 2.3, it suffices to prove that
$\unicode[STIX]{x1D705}(A)$
. Hence, by Proposition 2.3, it suffices to prove that
![]() $M/\mathfrak{m}_{A}M$
is weakly torsion-free over
$M/\mathfrak{m}_{A}M$
is weakly torsion-free over
![]() $B/\mathfrak{m}_{A}B$
, i.e. that for any
$B/\mathfrak{m}_{A}B$
, i.e. that for any
![]() $\unicode[STIX]{x1D706}\in B$
and any
$\unicode[STIX]{x1D706}\in B$
and any
![]() $m\in M$
, the relation
$m\in M$
, the relation
![]() $\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
implies that
$\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
implies that
![]() $\unicode[STIX]{x1D706}\in \mathfrak{m}_{A}B$
or
$\unicode[STIX]{x1D706}\in \mathfrak{m}_{A}B$
or
![]() $m\in \mathfrak{m}_{B}M$
. So, let
$m\in \mathfrak{m}_{B}M$
. So, let
![]() $\unicode[STIX]{x1D706}\in B$
and
$\unicode[STIX]{x1D706}\in B$
and
![]() $m\in M$
be such that
$m\in M$
be such that
![]() $\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
and
$\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
and
![]() $\unicode[STIX]{x1D706}\notin \mathfrak{m}_{A}B$
; let us prove that
$\unicode[STIX]{x1D706}\notin \mathfrak{m}_{A}B$
; let us prove that
![]() $m\in \mathfrak{m}_{B}M$
. By [Reference Simon and StrookerSS06, 2.7], we know that the image
$m\in \mathfrak{m}_{B}M$
. By [Reference Simon and StrookerSS06, 2.7], we know that the image
![]() $\overline{\unicode[STIX]{x1D6E5}}$
of
$\overline{\unicode[STIX]{x1D6E5}}$
of
![]() $\unicode[STIX]{x1D6E5}$
is a generator of the socle of the Gorenstein ring
$\unicode[STIX]{x1D6E5}$
is a generator of the socle of the Gorenstein ring
![]() $B/\mathfrak{m}_{A}B$
. Hence,
$B/\mathfrak{m}_{A}B$
. Hence,
![]() $(\overline{\unicode[STIX]{x1D6E5}})\subset (\overline{\unicode[STIX]{x1D706}})$
in
$(\overline{\unicode[STIX]{x1D6E5}})\subset (\overline{\unicode[STIX]{x1D706}})$
in
![]() $B/\mathfrak{m}_{A}B$
. Since
$B/\mathfrak{m}_{A}B$
. Since
![]() $\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
, this implies that
$\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
, this implies that
![]() $\unicode[STIX]{x1D6E5}m\in \mathfrak{m}_{A}M$
. By Lemma 2.1, we get that
$\unicode[STIX]{x1D6E5}m\in \mathfrak{m}_{A}M$
. By Lemma 2.1, we get that
![]() $m\in \mathfrak{m}_{B}M$
, as required.
$m\in \mathfrak{m}_{B}M$
, as required.
Lastly let us prove that
![]() $A\rightarrow B$
is flat. Let
$A\rightarrow B$
is flat. Let
![]() $E\rightarrow F$
be an injection of
$E\rightarrow F$
be an injection of
![]() $A$
-modules. Let
$A$
-modules. Let
![]() $K$
be the kernel of
$K$
be the kernel of
![]() $E\otimes _{A}B\rightarrow F\otimes _{A}B$
. Since
$E\otimes _{A}B\rightarrow F\otimes _{A}B$
. Since
![]() $M$
is
$M$
is
![]() $B$
-flat,
$B$
-flat,
![]() $K\otimes _{B}M$
is the kernel of
$K\otimes _{B}M$
is the kernel of
![]() $E\otimes _{A}M\rightarrow F\otimes _{A}M$
, which is zero because
$E\otimes _{A}M\rightarrow F\otimes _{A}M$
, which is zero because
![]() $M$
is
$M$
is
![]() $A$
-flat. But
$A$
-flat. But
![]() $M$
is faithfully flat over
$M$
is faithfully flat over
![]() $B$
(because it is free and nonzero) and hence
$B$
(because it is free and nonzero) and hence
![]() $K=0$
.
$K=0$
.
Remark 2.4. If we replace the assumption (iii) of Theorem 1.1 with ‘
![]() $A$
and
$A$
and
![]() $B$
are Artin or
$B$
are Artin or
![]() $M$
is of finite type over
$M$
is of finite type over
![]() $A$
’, then we do not need to assume that the morphism
$A$
’, then we do not need to assume that the morphism
![]() $\unicode[STIX]{x1D711}:A\rightarrow B$
is local: it is then a consequence of the other hypotheses. Indeed, if there is an element
$\unicode[STIX]{x1D711}:A\rightarrow B$
is local: it is then a consequence of the other hypotheses. Indeed, if there is an element
![]() $a\in \mathfrak{m}_{A}$
such that
$a\in \mathfrak{m}_{A}$
such that
![]() $\unicode[STIX]{x1D711}(a)\in B^{\times }$
, then
$\unicode[STIX]{x1D711}(a)\in B^{\times }$
, then
![]() $M=\unicode[STIX]{x1D711}(a)M$
and hence
$M=\unicode[STIX]{x1D711}(a)M$
and hence
![]() $M=\mathfrak{m}_{A}M$
. Then
$M=\mathfrak{m}_{A}M$
. Then
![]() $M=0$
by Nakayama’s lemma (or because
$M=0$
by Nakayama’s lemma (or because
![]() $\mathfrak{m}_{A}$
is nilpotent if
$\mathfrak{m}_{A}$
is nilpotent if
![]() $A$
is Artin), which is a contradiction. On the other hand, if
$A$
is Artin), which is a contradiction. On the other hand, if
![]() $A$
is Artin, I am not sure that we really need the assumption that
$A$
is Artin, I am not sure that we really need the assumption that
![]() $B$
is Artin too.
$B$
is Artin too.
The following is a global version of Theorem 1.1.
Theorem 2.5. Let
![]() $f:X\rightarrow S$
be a morphism of locally Noetherian schemes. Assume that for any
$f:X\rightarrow S$
be a morphism of locally Noetherian schemes. Assume that for any
![]() $x\in X$
, the dimensions of the tangent spaces
$x\in X$
, the dimensions of the tangent spaces
![]() $T_{x}$
and
$T_{x}$
and
![]() $T_{f(x)}$
satisfy
$T_{f(x)}$
satisfy
Let
![]() ${\mathcal{M}}$
be a coherent
${\mathcal{M}}$
be a coherent
![]() ${\mathcal{O}}_{X}$
-module, flat over
${\mathcal{O}}_{X}$
-module, flat over
![]() $S$
. Then:
$S$
. Then:
-
(1)
 ${\mathcal{M}}$
is flat over
${\mathcal{M}}$
is flat over
 $X$
;
$X$
; -
(2) for each point
 $x\in \operatorname{Supp}({\mathcal{M}})$
,
$x\in \operatorname{Supp}({\mathcal{M}})$
,
 $f$
is flat at
$f$
is flat at
 $x$
, the fiber
$x$
, the fiber
 $f^{-1}(f(x))$
is a complete intersection of dimension zero at
$f^{-1}(f(x))$
is a complete intersection of dimension zero at
 $x$
(i.e. its local ring at
$x$
(i.e. its local ring at
 $x$
is a complete intersection of dimension zero) and
$x$
is a complete intersection of dimension zero) and
 $\dim T_{x}=\dim T_{f(x)}$
.
$\dim T_{x}=\dim T_{f(x)}$
.
In particular, if there exists a coherent
![]() ${\mathcal{O}}_{X}$
-module
${\mathcal{O}}_{X}$
-module
![]() ${\mathcal{M}}$
flat over
${\mathcal{M}}$
flat over
![]() $S$
whose support is
$S$
whose support is
![]() $X$
, then
$X$
, then
![]() $f$
is a complete intersection morphism of relative dimension zero (i.e.
$f$
is a complete intersection morphism of relative dimension zero (i.e.
![]() $f$
is flat and its fibers are zero-dimensional complete intersections).
$f$
is flat and its fibers are zero-dimensional complete intersections).
Proof. Note that the local ring of
![]() $X$
at a point
$X$
at a point
![]() $x$
is unaltered through the base change
$x$
is unaltered through the base change
![]() $\operatorname{Spec}{\mathcal{O}}_{S,f(x)}\rightarrow S$
. By [Reference BourbakiBou06, ch. II, § 3, no. 4, Proposition 14], the module
$\operatorname{Spec}{\mathcal{O}}_{S,f(x)}\rightarrow S$
. By [Reference BourbakiBou06, ch. II, § 3, no. 4, Proposition 14], the module
![]() ${\mathcal{M}}_{x}$
is flat over
${\mathcal{M}}_{x}$
is flat over
![]() ${\mathcal{O}}_{S,f(x)}$
. Since
${\mathcal{O}}_{S,f(x)}$
. Since
![]() $\dim T_{x}=\operatorname{edim}({\mathcal{O}}_{X,x})$
and
$\dim T_{x}=\operatorname{edim}({\mathcal{O}}_{X,x})$
and
![]() $\dim (T_{f(x)})=\operatorname{edim}({\mathcal{O}}_{S,f(x)})$
, we can apply Theorem 1.1 and
$\dim (T_{f(x)})=\operatorname{edim}({\mathcal{O}}_{S,f(x)})$
, we can apply Theorem 1.1 and
![]() ${\mathcal{M}}_{x}$
is flat over
${\mathcal{M}}_{x}$
is flat over
![]() ${\mathcal{O}}_{X,x}$
. This proves (1). If
${\mathcal{O}}_{X,x}$
. This proves (1). If
![]() $x\in \operatorname{Supp}({\mathcal{M}})$
, then
$x\in \operatorname{Supp}({\mathcal{M}})$
, then
![]() ${\mathcal{M}}_{x}\neq 0$
and by Theorem 1.1 we deduce that
${\mathcal{M}}_{x}\neq 0$
and by Theorem 1.1 we deduce that
![]() ${\mathcal{O}}_{X,x}$
is flat over
${\mathcal{O}}_{X,x}$
is flat over
![]() ${\mathcal{O}}_{S,f(x)}$
, that these rings have the same embedding dimension and that
${\mathcal{O}}_{S,f(x)}$
, that these rings have the same embedding dimension and that
![]() ${\mathcal{O}}_{X,x}/\mathfrak{m}{\mathcal{O}}_{X,x}$
is a zero-dimensional complete intersection (where
${\mathcal{O}}_{X,x}/\mathfrak{m}{\mathcal{O}}_{X,x}$
is a zero-dimensional complete intersection (where
![]() $\mathfrak{m}$
is the maximal ideal of
$\mathfrak{m}$
is the maximal ideal of
![]() ${\mathcal{O}}_{S,f(x)}$
). Since the latter ring
${\mathcal{O}}_{S,f(x)}$
). Since the latter ring
![]() ${\mathcal{O}}_{X,x}/\mathfrak{m}{\mathcal{O}}_{X,x}$
identifies with the local ring at
${\mathcal{O}}_{X,x}/\mathfrak{m}{\mathcal{O}}_{X,x}$
identifies with the local ring at
![]() $x$
of the fiber
$x$
of the fiber
![]() $X_{f(x)}$
, this proves (2).◻
$X_{f(x)}$
, this proves (2).◻
3 Application to the proof of Fermat’s last theorem
To conclude his proof, Wiles had to prove that a certain morphism of
![]() ${\mathcal{O}}$
-algebras
${\mathcal{O}}$
-algebras
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6F4}}:R_{\unicode[STIX]{x1D6F4}}\rightarrow T_{\unicode[STIX]{x1D6F4}}$
is an isomorphism and that
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6F4}}:R_{\unicode[STIX]{x1D6F4}}\rightarrow T_{\unicode[STIX]{x1D6F4}}$
is an isomorphism and that
![]() $T_{\unicode[STIX]{x1D6F4}}$
is a complete intersection over
$T_{\unicode[STIX]{x1D6F4}}$
is a complete intersection over
![]() ${\mathcal{O}}$
. Here
${\mathcal{O}}$
. Here
![]() ${\mathcal{O}}$
is the ring of integers of a finite extension of
${\mathcal{O}}$
is the ring of integers of a finite extension of
![]() $\mathbb{Q}_{\ell }$
,
$\mathbb{Q}_{\ell }$
,
![]() $R_{\unicode[STIX]{x1D6F4}}$
is the universal deformation ring for a Galois representation
$R_{\unicode[STIX]{x1D6F4}}$
is the universal deformation ring for a Galois representation
![]() $\overline{\unicode[STIX]{x1D70C}}:\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\rightarrow \operatorname{GL}_{2}(k)$
(where
$\overline{\unicode[STIX]{x1D70C}}:\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\rightarrow \operatorname{GL}_{2}(k)$
(where
![]() $k$
is the residue field of
$k$
is the residue field of
![]() ${\mathcal{O}}$
) and
${\mathcal{O}}$
) and
![]() $T_{\unicode[STIX]{x1D6F4}}$
is a certain Hecke algebra. The proof proceeds in two steps: first it is proved for
$T_{\unicode[STIX]{x1D6F4}}$
is a certain Hecke algebra. The proof proceeds in two steps: first it is proved for
![]() $\unicode[STIX]{x1D6F4}=\varnothing$
(the ‘minimal case’), then the general case is deduced from this one using some numerical criterion for complete intersections. To handle the minimal case, Wiles constructs a system of sets
$\unicode[STIX]{x1D6F4}=\varnothing$
(the ‘minimal case’), then the general case is deduced from this one using some numerical criterion for complete intersections. To handle the minimal case, Wiles constructs a system of sets
![]() $Q_{n}$
,
$Q_{n}$
,
![]() $n\geqslant 1$
, where
$n\geqslant 1$
, where
![]() $Q_{n}$
is a set of primes congruent to 1 mod
$Q_{n}$
is a set of primes congruent to 1 mod
![]() $\ell ^{n}$
with some other ad hoc properties. Then, by considering a kind of ‘patching’ of the morphisms
$\ell ^{n}$
with some other ad hoc properties. Then, by considering a kind of ‘patching’ of the morphisms
![]() $\unicode[STIX]{x1D6F7}_{Q_{n}}:R_{Q_{n}}\rightarrow T_{Q_{n}}$
, Wiles manages to prove the desired result for
$\unicode[STIX]{x1D6F7}_{Q_{n}}:R_{Q_{n}}\rightarrow T_{Q_{n}}$
, Wiles manages to prove the desired result for
![]() $\unicode[STIX]{x1D6F4}=\varnothing$
. Among other things, the proof relied on the fact (due to Mazur and Ribet) that the homology of the modular curve is a free module of rank 2 over
$\unicode[STIX]{x1D6F4}=\varnothing$
. Among other things, the proof relied on the fact (due to Mazur and Ribet) that the homology of the modular curve is a free module of rank 2 over
![]() $T_{\varnothing }$
(known as a ‘multiplicity one’ result). Diamond improved the method in [Reference DiamondDia97]: by patching the modules as well as the algebras, he managed to remove multiplicity one as an ingredient of the proof of Fermat’s last theorem. His proof relies on his freeness criterion [Reference DiamondDia97, 2.1]. Since we only want to illustrate how our Theorem 1.1 can be used to avoid the patching method and the use of Taylor–Wiles systems, we will work in the rather restrictive setting of [Reference Darmon, Diamond and TaylorDDT97] and [Reference DiamondDia97]. We use their notations and statements in the sequel.
$T_{\varnothing }$
(known as a ‘multiplicity one’ result). Diamond improved the method in [Reference DiamondDia97]: by patching the modules as well as the algebras, he managed to remove multiplicity one as an ingredient of the proof of Fermat’s last theorem. His proof relies on his freeness criterion [Reference DiamondDia97, 2.1]. Since we only want to illustrate how our Theorem 1.1 can be used to avoid the patching method and the use of Taylor–Wiles systems, we will work in the rather restrictive setting of [Reference Darmon, Diamond and TaylorDDT97] and [Reference DiamondDia97]. We use their notations and statements in the sequel.
Let us prove that
![]() $\unicode[STIX]{x1D6F7}_{\varnothing }$
is an isomorphism. Let
$\unicode[STIX]{x1D6F7}_{\varnothing }$
is an isomorphism. Let
![]() $\unicode[STIX]{x1D706}$
be a uniformizer of
$\unicode[STIX]{x1D706}$
be a uniformizer of
![]() ${\mathcal{O}}$
. By [Reference Darmon, Diamond and TaylorDDT97, 2.49] (note that we only use it for
${\mathcal{O}}$
. By [Reference Darmon, Diamond and TaylorDDT97, 2.49] (note that we only use it for
![]() $n=1$
, so here also the proof can be simplified), there exists a finite set of prime numbers
$n=1$
, so here also the proof can be simplified), there exists a finite set of prime numbers
![]() $Q$
such that:
$Q$
such that:
-
–
 $\operatorname{edim}(\overline{R_{Q}})\leqslant \#Q=:r$
, where
$\operatorname{edim}(\overline{R_{Q}})\leqslant \#Q=:r$
, where
 $\overline{R_{Q}}=R_{Q}\otimes _{{\mathcal{O}}}k=R_{Q}/\unicode[STIX]{x1D706}R_{Q}$
;
$\overline{R_{Q}}=R_{Q}\otimes _{{\mathcal{O}}}k=R_{Q}/\unicode[STIX]{x1D706}R_{Q}$
; -
– for any
 $q\in Q$
,
$q\in Q$
,
 $q\equiv 1~(\ell )$
,
$q\equiv 1~(\ell )$
,
 $\overline{\unicode[STIX]{x1D70C}}$
is unramified at
$\overline{\unicode[STIX]{x1D70C}}$
is unramified at
 $q$
and
$q$
and
 $\overline{\unicode[STIX]{x1D70C}}(\operatorname{Frob}_{q})$
has distinct eigenvalues.
$\overline{\unicode[STIX]{x1D70C}}(\operatorname{Frob}_{q})$
has distinct eigenvalues.
Let
![]() $G$
be the
$G$
be the
![]() $\ell$
-Sylow subgroup of
$\ell$
-Sylow subgroup of
![]() $\prod _{q\in Q}(\mathbb{Z}/q\mathbb{Z})^{\times }$
. We endow
$\prod _{q\in Q}(\mathbb{Z}/q\mathbb{Z})^{\times }$
. We endow
![]() $R_{Q}$
with the structure of an
$R_{Q}$
with the structure of an
![]() ${\mathcal{O}}[G]$
-algebra as in [Reference Darmon, Diamond and TaylorDDT97, § 2.8]. Let
${\mathcal{O}}[G]$
-algebra as in [Reference Darmon, Diamond and TaylorDDT97, § 2.8]. Let
![]() $N$
be the integer
$N$
be the integer
![]() $N_{\varnothing }$
of [Reference Darmon, Diamond and TaylorDDT97, (4.2.1)] and
$N_{\varnothing }$
of [Reference Darmon, Diamond and TaylorDDT97, (4.2.1)] and
![]() $M=p^{2}\prod _{q\in Q}q$
, where
$M=p^{2}\prod _{q\in Q}q$
, where
![]() $p$
is a well-chosen auxiliary prime (see [Reference Darmon, Diamond and TaylorDDT97, § 4.3]). Consider the group
$p$
is a well-chosen auxiliary prime (see [Reference Darmon, Diamond and TaylorDDT97, § 4.3]). Consider the group
and let
![]() $X_{\unicode[STIX]{x1D6E4}}$
be the associated modular curve. By [Reference Darmon, Diamond and TaylorDDT97, 4.10], there is an isomorphism
$X_{\unicode[STIX]{x1D6E4}}$
be the associated modular curve. By [Reference Darmon, Diamond and TaylorDDT97, 4.10], there is an isomorphism
![]() $T_{Q}\rightarrow T_{\mathfrak{m}}^{\prime }$
, where
$T_{Q}\rightarrow T_{\mathfrak{m}}^{\prime }$
, where
![]() $T^{\prime }$
is the algebra of Hecke operators acting on
$T^{\prime }$
is the algebra of Hecke operators acting on
![]() $H^{1}(X_{\unicode[STIX]{x1D6E4}},{\mathcal{O}})$
and
$H^{1}(X_{\unicode[STIX]{x1D6E4}},{\mathcal{O}})$
and
![]() $\mathfrak{m}$
is a certain maximal ideal of
$\mathfrak{m}$
is a certain maximal ideal of
![]() $T^{\prime }$
. Consider the
$T^{\prime }$
. Consider the
![]() $T_{\mathfrak{m}}^{\prime }$
-module
$T_{\mathfrak{m}}^{\prime }$
-module
of elements on which complex conjugation acts by
![]() $-1$
. We can view
$-1$
. We can view
![]() $H$
as a module over
$H$
as a module over
![]() ${\mathcal{O}}[G]$
,
${\mathcal{O}}[G]$
,
![]() $R_{Q}$
, or
$R_{Q}$
, or
![]() $T_{Q}$
via the
$T_{Q}$
via the
![]() ${\mathcal{O}}$
-algebra morphisms
${\mathcal{O}}$
-algebra morphisms
Theorem 3.1. With the above notation:
-
(i)
 $H$
is free over
$H$
is free over
 $T_{Q}$
;
$T_{Q}$
; -
(ii)
 $T_{Q}$
is free over
$T_{Q}$
is free over
 ${\mathcal{O}}[G]$
;
${\mathcal{O}}[G]$
; -
(iii)
 $T_{Q}$
is a relative complete intersection over
$T_{Q}$
is a relative complete intersection over
 ${\mathcal{O}}[G]$
(hence also over
${\mathcal{O}}[G]$
(hence also over
 ${\mathcal{O}}$
);
${\mathcal{O}}$
); -
(iv)
 $\unicode[STIX]{x1D6F7}_{Q}:R_{Q}\rightarrow T_{Q}$
is an isomorphism.
$\unicode[STIX]{x1D6F7}_{Q}:R_{Q}\rightarrow T_{Q}$
is an isomorphism.
Proof. By [Reference DiamondDia97, Lemma 3.2],
![]() $\overline{H}=H/\unicode[STIX]{x1D706}H$
is free over
$\overline{H}=H/\unicode[STIX]{x1D706}H$
is free over
![]() $k[G]$
. Note that there is an isomorphism
$k[G]$
. Note that there is an isomorphism
![]() ${\mathcal{O}}[G]\simeq {\mathcal{O}}[[S_{1},\ldots ,S_{r}]]/((1+S_{1})^{\unicode[STIX]{x1D6FC}_{1}}-1,\ldots ,(1+S_{r})^{\unicode[STIX]{x1D6FC}_{r}}-1)$
, where the
${\mathcal{O}}[G]\simeq {\mathcal{O}}[[S_{1},\ldots ,S_{r}]]/((1+S_{1})^{\unicode[STIX]{x1D6FC}_{1}}-1,\ldots ,(1+S_{r})^{\unicode[STIX]{x1D6FC}_{r}}-1)$
, where the
![]() $\unicode[STIX]{x1D6FC}_{i}$
are the cardinalities of the
$\unicode[STIX]{x1D6FC}_{i}$
are the cardinalities of the
![]() $l$
-Sylow subgroups of the
$l$
-Sylow subgroups of the
![]() $(\mathbb{Z}/q\mathbb{Z})^{\times }$
for
$(\mathbb{Z}/q\mathbb{Z})^{\times }$
for
![]() $q\in Q$
. In particular,
$q\in Q$
. In particular,
![]() $\unicode[STIX]{x1D6FC}_{i}\geqslant \ell \geqslant 2$
and it follows that
$\unicode[STIX]{x1D6FC}_{i}\geqslant \ell \geqslant 2$
and it follows that
![]() $\operatorname{edim}(k[G])=r$
. We can apply Theorem 1.1 to the morphism
$\operatorname{edim}(k[G])=r$
. We can apply Theorem 1.1 to the morphism
![]() $k[G]\rightarrow \overline{R_{Q}}$
and the module
$k[G]\rightarrow \overline{R_{Q}}$
and the module
![]() $\overline{H}$
. We get that
$\overline{H}$
. We get that
![]() $\overline{H}$
is free over
$\overline{H}$
is free over
![]() $\overline{R_{Q}}$
, and that
$\overline{R_{Q}}$
, and that
![]() $\overline{R_{Q}}$
is free and is a relative complete intersection over
$\overline{R_{Q}}$
is free and is a relative complete intersection over
![]() $k[G]$
. In particular,
$k[G]$
. In particular,
![]() $\overline{R_{Q}}\rightarrow \overline{T_{Q}}$
must be injective (otherwise
$\overline{R_{Q}}\rightarrow \overline{T_{Q}}$
must be injective (otherwise
![]() $\overline{H}$
would have torsion over
$\overline{H}$
would have torsion over
![]() $\overline{R_{Q}}$
). Since it is already known to be surjective, it is an isomorphism. We have proved all the statements after
$\overline{R_{Q}}$
). Since it is already known to be surjective, it is an isomorphism. We have proved all the statements after
![]() $\otimes _{{\mathcal{O}}}k$
. Since
$\otimes _{{\mathcal{O}}}k$
. Since
![]() $T_{Q}$
is free over
$T_{Q}$
is free over
![]() ${\mathcal{O}}$
, the theorem now follows from Lemma 3.2 below.◻
${\mathcal{O}}$
, the theorem now follows from Lemma 3.2 below.◻
Lemma 3.2. Let
![]() ${\mathcal{O}}$
be a Noetherian local ring with maximal ideal
${\mathcal{O}}$
be a Noetherian local ring with maximal ideal
![]() $\mathfrak{m}$
and residue field
$\mathfrak{m}$
and residue field
![]() $k$
.
$k$
.
-
(i) Let
 $f:M\rightarrow N$
be a morphism of finite-type
$f:M\rightarrow N$
be a morphism of finite-type
 ${\mathcal{O}}$
-modules. Assume that
${\mathcal{O}}$
-modules. Assume that
 $N$
is free over
$N$
is free over
 ${\mathcal{O}}$
and that
${\mathcal{O}}$
and that
 $f\otimes _{{\mathcal{O}}}k$
is an isomorphism. Then
$f\otimes _{{\mathcal{O}}}k$
is an isomorphism. Then
 $f$
is an isomorphism.
$f$
is an isomorphism. -
(ii) Let
 $A$
be a finite
$A$
be a finite
 ${\mathcal{O}}$
-algebra and
${\mathcal{O}}$
-algebra and
 $M$
be an
$M$
be an
 $A$
-module which is free of finite rank over
$A$
-module which is free of finite rank over
 ${\mathcal{O}}$
. If
${\mathcal{O}}$
. If
 $M\otimes _{{\mathcal{O}}}k$
is free over
$M\otimes _{{\mathcal{O}}}k$
is free over
 $A\otimes _{{\mathcal{O}}}k$
, then
$A\otimes _{{\mathcal{O}}}k$
, then
 $M$
is free over
$M$
is free over
 $A$
.
$A$
. -
(iii) Assume that
 ${\mathcal{O}}$
is complete. Let
${\mathcal{O}}$
is complete. Let
 $A\rightarrow B$
be a morphism of finite local
$A\rightarrow B$
be a morphism of finite local
 ${\mathcal{O}}$
-algebras, with
${\mathcal{O}}$
-algebras, with
 $B$
free over
$B$
free over
 ${\mathcal{O}}$
. If
${\mathcal{O}}$
. If
 $B\otimes _{{\mathcal{O}}}k$
is a relative complete intersection over
$B\otimes _{{\mathcal{O}}}k$
is a relative complete intersection over
 $A\otimes _{{\mathcal{O}}}k$
, then
$A\otimes _{{\mathcal{O}}}k$
, then
 $B$
is a relative complete intersection over
$B$
is a relative complete intersection over
 $A$
(i.e. the ring
$A$
(i.e. the ring
 $B/\mathfrak{m}_{A}B$
is a complete intersection).
$B/\mathfrak{m}_{A}B$
is a complete intersection).
Proof. These are standard consequences of Nakayama’s lemma. ◻
Remark 3.3. By [Reference Darmon, Diamond and TaylorDDT97, Corollaries 2.45 and 3.32], the canonical morphisms
![]() $R_{Q}\rightarrow R_{\varnothing }$
and
$R_{Q}\rightarrow R_{\varnothing }$
and
![]() $T_{Q}\rightarrow T_{\varnothing }$
induce isomorphisms
$T_{Q}\rightarrow T_{\varnothing }$
induce isomorphisms
![]() $R_{Q}/\mathfrak{a}_{Q}R_{Q}\simeq R_{\varnothing }$
and
$R_{Q}/\mathfrak{a}_{Q}R_{Q}\simeq R_{\varnothing }$
and
![]() $T_{Q}/\mathfrak{a}_{Q}T_{Q}\simeq T_{\varnothing }$
, where
$T_{Q}/\mathfrak{a}_{Q}T_{Q}\simeq T_{\varnothing }$
, where
![]() $\mathfrak{a}_{Q}$
is the augmentation ideal of
$\mathfrak{a}_{Q}$
is the augmentation ideal of
![]() ${\mathcal{O}}[G]$
(i.e. the ideal generated by
${\mathcal{O}}[G]$
(i.e. the ideal generated by
![]() $S_{1},\ldots ,S_{R}$
). Hence, from Theorem 3.1, it follows immediately that
$S_{1},\ldots ,S_{R}$
). Hence, from Theorem 3.1, it follows immediately that
![]() $\unicode[STIX]{x1D6F7}_{\varnothing }:R_{\varnothing }\rightarrow T_{\varnothing }$
is an isomorphism and
$\unicode[STIX]{x1D6F7}_{\varnothing }:R_{\varnothing }\rightarrow T_{\varnothing }$
is an isomorphism and
![]() $T_{\varnothing }$
is a complete intersection over
$T_{\varnothing }$
is a complete intersection over
![]() ${\mathcal{O}}$
.
${\mathcal{O}}$
.
Acknowledgements
I warmly thank Bart de Smit for raising his conjecture and for pointing out to me the freeness criterion [Reference DiamondDia97, Theorem 2.1]. I also thank Michel Raynaud and Stefano Morra for interesting conversations, and the anonymous referee for valuable comments that helped to clarify the exposition.