Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-25T00:46:52.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-stationary smooth geometric structures for contracting measurable cocycles

Published online by Cambridge University Press:  28 June 2017

KARIN MELNICK
KARIN MELNICK*
Affiliation:
Department of Mathematics, 4176 Campus Drive, University of Maryland, College Park, MD 20742, USA email karin@math.umd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We implement a differential-geometric approach to normal forms for contracting measurable cocycles to 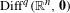$\operatorname{Diff}^{q}(\mathbb{R}^{n},\mathbf{0})$, 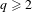$q\geq 2$. We obtain resonance polynomial normal forms for the contracting cocycle and its centralizer, via 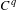$C^{q}$ changes of coordinates. These are interpreted as non-stationary invariant differential-geometric structures. We also consider the case of contracted foliations in a manifold, and obtain 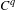$C^{q}$ homogeneous structures on leaves for an action of the group of subresonance polynomial diffeomorphisms together with translations.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 2 , February 2019 , pp. 392 - 424
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Araújo, V., Bufetov, A. and Filip, S.. On Hölder-continuity of Oseledets subspaces. J. Lond. Math. Soc. (2) 93 (2016), 194–218.Google Scholar
Barreira, L. and Pesin, Y.. Introduction to Smooth Ergodic Theory. American Mathematical Society, Providence, RI, 2013.Google Scholar
Feres, R.. Rigid geometric structures and actions of semisimple Lie groups. Rigidité, Groupe Fondamentale, et Dynamique. Vol. 13. Société Mathématique de France, Paris, 2002, pp. 121–166.Google Scholar
Feres, R.. A differential-geometric view of normal forms of contractions. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 103–121.Google Scholar
Fisher, D. and Margulis, G.. Almost isometric actions, property (T), and local rigidity. Invent. Math. 162 (2005), 19–80.Google Scholar
Fisher, D. and Margulis, G.. Local rigidity of affine actions of higher rank groups and lattices. Ann. of Math. (2) 170(1) (2009), 67–122.Google Scholar
Guysinsky, M.. The theory of non-stationary normal forms. Ergod. Th. & Dynam. Sys. 21 (2001), 845–862.Google Scholar
Guysinsky, M. and Katok, A.. Normal forms and invariant geometric structures for dynamical systems with invariant contracting foliations. Math. Res. Lett. 5 (1998), 149–163.Google Scholar
Kalinin, B. and Katok, A.. Invariant measures for actions of higher rank abelian groups. Smooth Ergodic Theory and its Applications (Seattle, WA, 1999) (Proceedings of Symposia in Pure Mathematics, 69) . American Mathematical Society, Providence, RI, 2001, pp. 593–637.Google Scholar
Kalinin, B. and Sadovskaya, V.. Global rigidity for totally nonsymplectic Anosov Z k actions. Geom. Topol. 10 (2006), 929–954.Google Scholar
Kalinin, B. and Sadovskaya, V.. Non-stationary normal forms on contracting foliations: Smoothness and homogeneity. Geom. Ded. 183 (2016), 181–194.Google Scholar
Kalinin, B. and Sadovskaya, V.. Normal forms for non-uniform contractions. J. Mod. Dyn., to appear.Google Scholar
Katok, A. and Spatzier, R.. Differential rigidity of Anosov actions of higher rank abelian groups and algebraic lattice actions. Tr. Mat. Inst. Steklova 216 (1997).Google Scholar
Kobayashi, S.. Transformation Groups in Differential Geometry. Springer, Berlin, 1995.Google Scholar
Li, W. and Lu, K.. Sternberg theorems for random dynamical systems. Comm. Pure Appl. Math. 58 (2005), 941–988.Google Scholar
Ruelle, D.. Ergodic theory of differentiable dynamical systems. Publ. Math. Inst. Hautes Études Sci. 50 (1978), 27–58.Google Scholar
Sternberg, S.. Local contractions and a theorem of Poincaré. Amer. J. Math. 79(4) (1957), 809–824.Google Scholar