Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-19T14:19:32.883Z Has data issue: false hasContentIssue false
  • English
  • Français

QUASIRANDOM GROUP ACTIONS

Part of: Probabilistic methods in group theory Representation theory of groups Special aspects of infinite or finite groups Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  30 August 2016

NICK GILL
NICK GILL*
Affiliation:
Department of Mathematics, University of South Wales, Treforest, CF37 1DL, UK; nick.gill@southwales.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 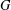$G$ be a finite group acting transitively on a set 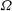$\unicode[STIX]{x1D6FA}$. We study what it means for this action to be quasirandom, thereby generalizing Gowers’ study of quasirandomness in groups. We connect this notion of quasirandomness to an upper bound for the convolution of functions associated with the action of 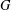$G$ on 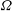$\unicode[STIX]{x1D6FA}$. This convolution bound allows us to give sufficient conditions such that sets 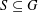$S\subseteq G$ and 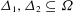$\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2}\subseteq \unicode[STIX]{x1D6FA}$ contain elements 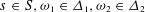$s\in S,\unicode[STIX]{x1D714}_{1}\in \unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D714}_{2}\in \unicode[STIX]{x1D6E5}_{2}$ such that 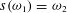$s(\unicode[STIX]{x1D714}_{1})=\unicode[STIX]{x1D714}_{2}$. Other consequences include an analogue of ‘the Gowers trick’ of Nikolov and Pyber for general group actions, a sum-product type theorem for large subsets of a finite field, as well as applications to expanders and to the study of the diameter and width of a finite simple group.

MSC classification

Primary: 60B15: Probability measures on groups or semigroups, Fourier transforms, factorization
Secondary: 20P05: Probabilistic methods in group theory 20D60: Arithmetic and combinatorial problems 20F70: Algebraic geometry over groups; equations over groups
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e24
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2016

References

Babai, L., ‘On the diameter of Eulerian orientations of graphs’, inProceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithms (ACM, New York, 2006), 822–831.Google Scholar
Babai, L., Nikolov, N. and Pyber, L., ‘Product growth and mixing in finite groups’, inProceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms (ACM, New York, 2008), 248–257.Google Scholar
Babai, L. and Seress, Á., ‘On the diameter of permutation groups’, European J. Combin. 13(4) (1992), 231–243.CrossRefGoogle Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I. The user language’, J. Symbolic Comput. 24(3–4) (1997), 235–265. Computational algebra and number theory (London, 1993).CrossRefGoogle Scholar
Bourgain, J. and Gamburd, A., ‘On the spectral gap for finitely-generated subgroups of SU(2)’, Invent. Math. 171(1) (2008), 83–121.CrossRefGoogle Scholar
Bourgain, J. and Gamburd, A., ‘Uniform expansion bounds for Cayley graphs of SL2(F p )’, Ann. of Math. (2) 167(2) (2008), 625–642.CrossRefGoogle Scholar
Breuillard, E., Green, B. and Tao, T., ‘Approximate subgroups of linear groups’, Geom. Funct. Anal. 21(4) (2011), 774–819.CrossRefGoogle Scholar
Bourgain, J. and Yehudayoff, A., ‘Monotone expansion’, inSTOC’12—Proceedings of the 2012 ACM Symposium on Theory of Computing (ACM, New York, 2012), 1061–1078.Google Scholar
Fulton, W. and Harris, J., Representation Theory, Graduate Texts in Mathematics, 129 , (Springer, New York, 1991), A first course, Readings in Mathematics.Google Scholar
The GAP Group, GAP–Groups, Algorithms, and Programming, Version 4412, 2008.Google Scholar
Garaev, M. Z., ‘The sum-product estimate for large subsets of prime fields’, Proc. Amer. Math. Soc. 136(8) (2008), 2735–2739.CrossRefGoogle Scholar
Gill, N., Pyber, L., Short, I. and Szabó, E., ‘On the product decomposition conjecture for finite simple groups’, Groups Geom. Dyn. 7(4) (2013), 867–882.CrossRefGoogle Scholar
Gowers, W. T., ‘Quasirandom groups’, Comb. Probab. Comp. 17 (2008), 363–387.CrossRefGoogle Scholar
Hart, D. and Iosevich, A., ‘Sums and products in finite fields: an integral geometric viewpoint’, Radon transforms, geometry, and wavelets, Contemp. Math. 464 (2008), 129–135.CrossRefGoogle Scholar
Hart, D., Iosevich, A., Koh, D. and Rudnev, M., ‘Averages over hyperplanes, sum-product theory in vector space over finite fields and the Erdös–Falconer distance conjecture’, Trans. Amer. Math. Soc. 363(6) (2011), 3255–3275.CrossRefGoogle Scholar
Hart, D., Iosevich, A., Koh, D. and Rudnev, M., ‘Growth in SL3(ℤ/pℤ)’, J. Eur. Math. Soc. 13(3) (2011), 761–851.Google Scholar
Helfgott, H. A., ‘Growth and generation in SL2(ℤ/pℤ)’, Ann. of Math. (2) 167(2) (2008), 601–623.CrossRefGoogle Scholar
Hoory, S., Linial, N. and Wigderson, A., ‘Expander graphs and their applications’, Bull. Amer. Math. Soc. (N.S.) 43(4) (2006), 439–561. (electronic).CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (AMS Chelsea Publishing, Providence, RI, 2006), Corrected reprint of the 1976 original [Academic Press, New York].Google Scholar
Landazuri, V. and Seitz, G. M., ‘On the minimal degrees of projective representations of the finite Chevalley groups’, J. Algebra 32 (1974), 418–443.CrossRefGoogle Scholar
Liebeck, M. W., Nikolov, N. and Shalev, A., ‘Product decompositions in finite simple groups’, Bull. Lond. Math. Soc. 44(3) (2012), 469–472.CrossRefGoogle Scholar
Liebeck, M. W. and Shalev, A., ‘Diameters of finite simple groups: sharp bounds and applications’, Ann. of Math. (2) 154(2) (2001), 383–406.CrossRefGoogle Scholar
Nikolov, N. and Pyber, L., ‘Product decompositions of quasirandom groups and a Jordan-type theorem’, J. Eur. Math. Soc. 13(4) (2011), 1063–1077.CrossRefGoogle Scholar
Pyber, L. and Szabó, E., ‘Growth in finite simple groups of Lie type of bounded rank’, J. Amer. Math. Soc. 29 (2016), 95–146.CrossRefGoogle Scholar
Rasala, R., ‘On the minimal degrees of characters of S n ’, J. Algebra 45(1) (1977), 132–181.CrossRefGoogle Scholar
Reingold, O., Vadhan, S. and Wigderson, A., ‘Entropy waves, the zig-zag graph product, and new constant-degree expanders’, Ann. of Math. (2) 155(1) (2002), 157–187.CrossRefGoogle Scholar
Sarnak, P. and Xue, X. X., ‘Bounds for multiplicities of automorphic representations’, Duke Math. J. 64(1) (1991), 207–227.CrossRefGoogle Scholar
Szegedy, B., ‘Limits of kernel operators and the spectral regularity lemma’, European J. Combin. 32(7) (2011), 1156–1167.CrossRefGoogle Scholar
Tiep, P. H. and Zalesskii, A. E., ‘Minimal characters of the finite classical groups’, Comm. Algebra 24(6) (1996), 2093–2167.CrossRefGoogle Scholar
Vinh, L. A., ‘The Szemerédi–Trotter type theorem and the sum-product estimate in finite fields’, European J. Combin. 32(8) (2011), 1177–1181.CrossRefGoogle Scholar
Yehudayoff, A., ‘Proving expansion in three steps’, ACM SIGACT News 43(3) (2012), 67–84.CrossRefGoogle Scholar