Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-25T01:47:56.129Z Has data issue: false hasContentIssue false
  • English
  • Français

Vertically localised equilibrium solutions in large-eddy simulations of homogeneous shear flow

Published online by Cambridge University Press:  18 August 2017

Atsushi Sekimoto Open the ORCID record for Atsushi Sekimoto [Opens in a new window]  and
Javier Jiménez Open the ORCID record for Javier Jiménez [Opens in a new window]
Atsushi Sekimoto*
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
Javier Jiménez
Affiliation:
School of Aeronautics, Universidad Politécnica de Madrid, 28040 Madrid, Spain
*
†Email address for correspondence: atsushi.sekimoto@monash.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Unstable equilibrium solutions in a homogeneous shear flow with sinuous (streamwise-shift-reflection and spanwise-shift-rotation) symmetry are numerically found in large-eddy simulations (LES) with no kinetic viscosity. The small-scale properties are determined by the mixing length scale 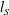$l_{S}$ used to define eddy viscosity, and the large-scale motion is induced by the mean shear at the integral scale, which is limited by the spanwise box dimension 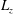$L_{z}$. The fraction 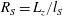$R_{S}=L_{z}/l_{S}$, which plays the role of a Reynolds number, is used as a numerical continuation parameter. It is shown that equilibrium solutions appear by a saddle-node bifurcation as 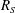$R_{S}$ increases, and that the flow structures resemble those in plane Couette flow with the same sinuous symmetry. The vortical structures of both lower- and upper-branch solutions become spontaneously localised in the vertical direction. The lower-branch solution is an edge state at low 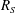$R_{S}$, and takes the form of a thin critical layer as 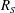$R_{S}$ increases, as in the asymptotic theory of generic shear flow at high Reynolds numbers. On the other hand, the upper-branch solutions are characterised by a tall velocity streak with multiscale multiple vortical structures. At the higher end of 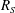$R_{S}$, an incipient multiscale structure is found. The LES turbulence occasionally visits vertically localised states whose vortical structure resembles the present vertically localised LES equilibria.

JFM classification

Turbulent Flows: Homogeneous turbulence Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 827 , 25 September 2017 , pp. 225 - 249
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, M., Mellibovsky, F., Roland, N. & Hof, B. 2013 Streamwise-localized solutions at the onset of turbulence in pipe flow. Phys. Rev. Lett. 110, 224502.Google Scholar
Blackburn, H. M., Hall, P. & Sherwin, S. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 726, R2.CrossRefGoogle Scholar
Cambon, C. & Scott, J. F. 1999 Linear and nonlinear models of anisotropic turbulence. Annu. Rev. Fluid Mech. 31, 1–53.Google Scholar
Champagne, F. H., Harris, V. G. & Corrsin, S. 1970 Experiments on nearly homogeneous turbulent shear flow. J. Fluid Mech. 41, 81–139.Google Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.Google Scholar
Cvitanović, P. 2013 Recurrent flows: the clockwork behind turbulence. J. Fluid Mech. 726, 1–4.CrossRefGoogle Scholar
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.Google Scholar
Deguchi, K. & Hall, P. 2014a Canonical exact coherent structures embedded in high Reynolds number flows. Phil. Trans. R. Soc. Lond. A 372, 20130352.Google ScholarPubMed
Deguchi, K. & Hall, P. 2014b The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.Google Scholar
Deguchi, K. & Hall, P. 2016 On the instability of vortex–wave interaction states. J. Fluid Mech. 802, 634–666.Google Scholar
Deguchi, K., Hall, P. & Walton, A. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.Google Scholar
Gerz, T., Schumann, U. & Elghobashi, S. E. 1989 Direct numerical simulation of stratified homogeneous turbulent shear flows. J. Fluid Mech. 200, 563–594.Google Scholar
Gibson, J. F. & Brand, E. 2014 Spanwise-localized solutions of planar shear flows. J. Fluid Mech. 745, 25–61.Google Scholar
Goto, S. 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–366.Google Scholar
Goto, S. 2012 Coherent structures and energy cascade in homogeneous turbulence. Prog. Theor. Phys. Suppl. 195, 139–156.Google Scholar
Gualtieri, P., Casciola, C. M., Benzi, R. & Piva, R. 2007 Preservation of statistical properties in large-eddy simulation of shear turbulence. J. Fluid Mech. 592, 471–494.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Hughes, T. J. R., Oberai, A. A. & Mazzei, L. 2001 Large eddy simulation of turbulent channel flows by the variational multiscale method. Phys. Fluids 13, 6.Google Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105, 044505.Google Scholar
Hwang, Y., Willis, A. P. & Cossu, C. 2016 Invariant solutions of minimal large-scale structures in turbulent channel flow for Re 𝜏 up to 1000. J. Fluid Mech. 802.CrossRefGoogle Scholar
Itano, T. & Generalis, S. C. 2009 Hairpin vortex solution in planar Couette flow: a tapestry of knotted vortices. Phys. Rev. Lett. 102 (11), 114501.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Jiménez, J.1987 Coherent structures and dynamical systems. In Proceedings of CTR Summer School, pp. 323–324. Stanford University.Google Scholar
Jiménez, J., Kawahara, G., Simens, M. P., Nagata, M. & Shiba, M. 2005 Characterization of near-wall turbulence in terms of equilibrium and ‘bursting’ solutions. Phys. Fluids 17, 015105.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Kawahara, G. 2005 Laminarization of minimal plane Couette flow: going beyond the basin of attraction of turbulence. Phys. Fluids 17, 041702.Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Kawahara, G., Uhlmann, M. & Van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.Google Scholar
Kerswell, R. R. & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Kim, J., Moin, P. & Moser., R. D. 1987 Turbulent statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kreilos, T. & Eckhardt, B. 2012 Periodic orbits near onset of chaos in plane couette flow. Chaos 22 (4), 047505.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Park, J. S. & Graham, M. D. 2015 Exact coherent states and connections to turbulent dynamics in minimal channel flow. J. Fluid Mech. 782, 430–454.Google Scholar
Piomelli, U., Rouhi, A. & Geurts, B. J. 2015 A grid-independent length scale for large-eddy simulations. J. Fluid Mech. 766, 499–527.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pumir, A. 1996 Turbulence in homogeneous shear flows. Phys. Fluids 8, 3112–3127.Google Scholar
Rawat, S., Cossu, C., Hwang, Y. & Rincon, F. 2015 On the self-sustained nature of large-scale motions in turbulent Couette flow. J. Fluid Mech. 782, 515–540.CrossRefGoogle Scholar
Rogers, M. M. & Moin, P. 1987 The structure of the vorticity field in homogeneous turbulent flows. J. Fluid Mech. 176, 33–66.Google Scholar
Sánchez, J. & Net, M. 2010 On the multiple shooting continuation of periodic orbits by Newton–Krylov methods. Intl J. Bifurcation Chaos 20, 43–61.Google Scholar
Sasaki, E., Kawahara, G., Sekimoto, A. & Jiménez, J. 2016 Unstable periodic orbits in plane Couette flow with the Smagorinsky model. J. Phys.: Conf. Ser. 708, 012003.Google Scholar
Schmiegel, A. & Eckhardt, B. 1997 Fractal stability border in plane Couette flow. Phys. Rev. Lett. 277, 197–225.Google Scholar
Schneider, T. M., Gibson, J. F. & Burke, J. 2010 Snakes and ladders: localized solutions of plane Couette flow. Phys. Rev. Lett. 104, 104501.CrossRefGoogle ScholarPubMed
Scovazzi, G., Jiménez, J. & Moin, P. 2001 LES of the very large scales in a Re 𝜏 = 920 channel. In Proc. Div. Fluid Dyn. pp. KF–5, American Physical Society.Google Scholar
Sekimoto, A., Dong, S. & Jiménez, J. 2016 Direct numerical simulation of statistically stationary and homogeneous shear turbulence and its relation to other shear flows. Phys. Fluids 28, 035101.CrossRefGoogle Scholar
Skufca, J. D., Yorke, J. A. & Eckhardt, B. 2006 Edge of chaos in a parallel shear flow. Phys. Rev. Lett. 96, 174101.CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. Mon. Weath. Rev. 91, 99–164.Google Scholar
Tavoularis, S. & Karnik, U. 1989 Further experiments on the evolution of turbulent stresses and scales in uniformly sheared turbulence. J. Fluid Mech. 204, 457–478.Google Scholar
Toh, S. & Itano, T. 2003 A periodic-like solution in channel flow. J. Fluid Mech. 481, 67–76.Google Scholar
van Veen, L. & Kawahara, G. 2011 Homoclinic tangle on the edge of shear turbulence. Phys. Rev. Lett. 107, 114501.Google Scholar
van Veen, L., Kawahara, G. & Matsumura, A. 2011 On matrix-free computation of 2D unstable manifolds. SIAM J. Sci. Comput. 33, 25–44.Google Scholar
van Veen, L., Kida, S. & Kawahara, G. 2006 Periodic motion representing isotropic turbulence. Fluid Dyn. Res. 38, 19–46.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Viswanath, D. 2009 The critical layer in pipe flow at high Reynolds number. Phil. Trans. R. Soc. Lond. A 367, 561–576.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.CrossRefGoogle Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98, 204501.CrossRefGoogle ScholarPubMed
Wedin, H. & Kerswell, R. 2004 Exact coherent structures in pipe flow: traveling wave solutions. J. Fluid Mech. 435, 333–371.Google Scholar
Yasuda, T., Goto, S. & Kawahara, G. 2014 Quasi-cyclic evolution of turbulence driven by a steady force in a periodic cube. Fluid Dyn. Res. 46, 061413.CrossRefGoogle Scholar
Zammert, S. & Eckhardt, B. 2015 Crisis bifurcations in plane Poiseuille flow. Phys. Rev. E 91, 041003.Google Scholar