Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-16T08:46:47.168Z Has data issue: false hasContentIssue false
  • English
  • Français

MEASURABLE REALIZATIONS OF ABSTRACT SYSTEMS OF CONGRUENCES

Part of: Polytopes and polyhedra Set theory Ergodic theory Classical measure theory

Published online by Cambridge University Press:  24 February 2020

CLINTON T. CONLEY ,
ANDREW S. MARKS  and
SPENCER T. UNGER
CLINTON T. CONLEY
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA; clintonc@andrew.cmu.edu
ANDREW S. MARKS
Affiliation:
Department of Mathematics, University of California at Los Angeles, USA; marks@math.ucla.edu
SPENCER T. UNGER
Affiliation:
Department of Mathematics, Hebrew University of Jerusalem, Israel; unger.spencer@mail.huji.ac.il

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An abstract system of congruences describes a way of partitioning a space into finitely many pieces satisfying certain congruence relations. Examples of abstract systems of congruences include paradoxical decompositions and $n$-divisibility of actions. We consider the general question of when there are realizations of abstract systems of congruences satisfying various measurability constraints. We completely characterize which abstract systems of congruences can be realized by nonmeager Baire measurable pieces of the sphere under the action of rotations on the $2$-sphere. This answers a question by Wagon. We also construct Borel realizations of abstract systems of congruences for the action of 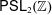$\mathsf{PSL}_{2}(\mathbb{Z})$ on 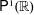$\mathsf{P}^{1}(\mathbb{R})$. The combinatorial underpinnings of our proof are certain types of decomposition of Borel graphs into paths. We also use these decompositions to obtain some results about measurable unfriendly colorings.

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 28A75: Length, area, volume, other geometric measure theory 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 52B45: Dissections and valuations (Hilbert's third problem, etc.)
Type
Foundations
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e10
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Cieśla, T. and Sabok, M., ‘Measurable Hall’s theorem for actions of abelian groups’, Preprint, 2019, arXiv:1903.02987.Google Scholar
Cohen, D. E., Combinatorial Group Theory: a Topological Approach (Cambridge University Press, Cambridge, 1989).CrossRefGoogle Scholar
Conley, C. T. and Kechris, A. S., ‘Measurable chromatic and independence numbers for ergodic graphs and group actions’, Groups Geom. Dyn. 7 (2013), 127–180.CrossRefGoogle Scholar
Diestel, R., Graph Theory, Fourth, Graduate Texts in Mathematics, 173 (Springer, Heidelberg, 2010).CrossRefGoogle Scholar
Dougherty, R. and Foreman, M., ‘Banach-Tarski decompositions using sets with the property of Baire’, J. Amer. Math. Soc. 7(1) (1994), 75–124.CrossRefGoogle Scholar
Dubins, L., Hirsch, M. W. and Karush, J., ‘Scissor congruence’, Israel J. Math. 1 (1963), 239–247.CrossRefGoogle Scholar
Gao, S. and Jackson, S., ‘Countable abelian group actions and hyperfinite equivalence relations’, Invent. Math. 201(1) (2015), 309–383.CrossRefGoogle Scholar
Gao, S., Jackson, S., Krohne, E. and Seward, B., ‘Forcing constructions and countable Borel equivalence relations’, Preprint, 2015.Google Scholar
Gardner, R. J., ‘Convex bodies equidecomposable by locally discrete groups of isometries’, Mathematika 32 (1985), 1–9.CrossRefGoogle Scholar
Grabowski, L., Máthé, A. and Pikhurko, O., ‘Measurable equidecompositions for group actions with an expansion property’, Preprint, 2016, arXiv:1601.02958.Google Scholar
Grabowski, L., Máthé, A. and Pikhurko, O., ‘Measurable circle squaring’, Ann. of Math (2) 185 (2017), 671–710.CrossRefGoogle Scholar
Hjorth, G. and Miller, B. D., ‘Ends of graphed equivalence relations, II’, Israel J. Math. 169 (2009), 393–415.CrossRefGoogle Scholar
Jackson, S., Kechris, A. S. and Louveau, A., ‘Countable Borel equivalence relations’, J. Math. Log. 2 (2002), 1–80.CrossRefGoogle Scholar
Katok, S., Fuchsian Groups, Chicago Lectures in Mathematics (Chicago, 1992).Google Scholar
Kechris, A. S., Classical Descriptive set Theory (Springer, New York, 1995).CrossRefGoogle Scholar
Kechris, A. S. and Marks, A. S., ‘Descriptive graph combinatorics’, Preprint, 2016.Google Scholar
Kechris, A. S., Solecki, S. and Todorcevic, S., ‘Borel chromatic numbers’, Adv. Math. 141 (1999), 1–44.CrossRefGoogle Scholar
Laczkovich, M., ‘Closed sets without measurable matching’, Proc. Amer. Math. Soc. 103(3) (1988), 894–896.CrossRefGoogle Scholar
Laczkovich, M., ‘Equidecomposability and discrepancy; a solution of Tarski’s circle-squaring problem’, J. Reine Angew. Math. 404 (1990), 77–117.Google Scholar
Laczkovich, M., ‘Decomposition of sets with small boundary’, J. Lond. Math. Soc. 46 (1992), 58–64.CrossRefGoogle Scholar
Lyons, R. and Nazarov, F., ‘Perfect matchings as IID factors of non-amenable groups’, European J. Combin. 32 (2011), 1115–1125.CrossRefGoogle Scholar
Marks, A. and Unger, S., ‘Baire measurable paradoxical decompositions via matchings’, Adv. Math. 289 (2016), 397–410.CrossRefGoogle Scholar
Marks, A. and Unger, S., ‘Borel circle squaring’, Ann. of Math. (2) 186 (2017), 581–605.CrossRefGoogle Scholar
Máthé, A., Measurable Equidecompositions, Proceedings of the International Congress of Mathematicians, 2 (World Sci. Publ., Hackensack, NJ, 2018), 1709–1728.Google Scholar
Miller, B. D., ‘Ends of graphed equivalence relations, I’, Israel J. Math. 169(1) (2009), 375–392.CrossRefGoogle Scholar
Nadkarni, M., ‘On the existence of a finite invariant measure’, Proc. Indian Acad. Sci. Math. Sci. 100 (1990), 203–220.CrossRefGoogle Scholar
Schneider, S. and Seward, B., ‘Locally nilpotent groups and hyperfinite equivalence relations’, Preprint.Google Scholar
Srivastava, S. M., A Course on Borel Sets (Springer, New York, 1998).CrossRefGoogle Scholar
Serre, J. P., A Course in Arithmetic, Graduate Texts in Mathematics, 7 (Springer, New York, 1973).CrossRefGoogle Scholar
Tarski, A., ‘Probléme 38’, Fund. Math. 7 (1925), 381.Google Scholar
Wagon, S., The Banach Tarski Paradox (Cambridge University Press, Cambridge, 1986).Google Scholar
Wehrung, F., ‘Baire paradoxical decompositions need at least six pieces’, Proc. Amer. Math. Soc. 121(2) (1994), 643–644.CrossRefGoogle Scholar