No CrossRef data available.
Article contents
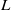 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
Published online by Cambridge University Press: 22 March 2013
Abstract
Let 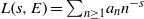 $L(s, E)= {\mathop{\sum }\nolimits}_{n\geq 1} {a}_{n} {n}^{- s} $ be the
$L(s, E)= {\mathop{\sum }\nolimits}_{n\geq 1} {a}_{n} {n}^{- s} $ be the 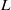 $L$-series corresponding to an elliptic curve
$L$-series corresponding to an elliptic curve 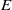 $E$ defined over
$E$ defined over 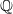 $ \mathbb{Q} $ and
$ \mathbb{Q} $ and  $\mathbf{u} = \mathop{\{ {u}_{m} \} }\nolimits_{m\geq 0} $ be a nondegenerate binary recurrence sequence. We prove that if
$\mathbf{u} = \mathop{\{ {u}_{m} \} }\nolimits_{m\geq 0} $ be a nondegenerate binary recurrence sequence. We prove that if 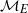 ${ \mathcal{M} }_{E} $ is the set of
${ \mathcal{M} }_{E} $ is the set of  $n$ such that
$n$ such that 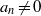 ${a}_{n} \not = 0$ and
${a}_{n} \not = 0$ and 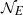 ${ \mathcal{N} }_{E} $ is the subset of
${ \mathcal{N} }_{E} $ is the subset of 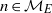 $n\in { \mathcal{M} }_{E} $ such that
$n\in { \mathcal{M} }_{E} $ such that  $\vert {a}_{n} \vert = \vert {u}_{m} \vert $ holds with some integer
$\vert {a}_{n} \vert = \vert {u}_{m} \vert $ holds with some integer 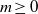 $m\geq 0$, then
$m\geq 0$, then 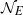 ${ \mathcal{N} }_{E} $ is of density
${ \mathcal{N} }_{E} $ is of density 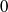 $0$ as a subset of
$0$ as a subset of 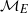 ${ \mathcal{M} }_{E} $.
${ \mathcal{M} }_{E} $.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 509 - 519
- Copyright
- Copyright ©2013 Australian Mathematical Publishing Association Inc.




