Two arithmetic functions 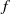$f$ and 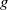$g$ form a Möbius pair if 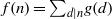$f(n)= {\mathop{\sum }\nolimits}_{d\mid n} g(d)$ for all natural numbers $n$. In that case, 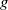$g$ can be expressed in terms of 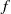$f$ by the familiar Möbius inversion formula of elementary number theory. In a previous paper, the first-named author showed that if the members 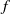$f$ and 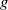$g$ of a Möbius pair are both finitely supported, then both functions vanish identically. Here we prove two significantly stronger versions of this uncertainty principle. A corollary is that in a nonzero Möbius pair, one cannot have both 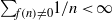${\mathop{\sum }\nolimits}_{f(n)\not = 0} 1/ n\lt \infty $ and 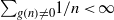${\mathop{\sum }\nolimits}_{g(n)\not = 0} 1/ n\lt \infty $.