Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-23T12:38:42.202Z Has data issue: false hasContentIssue false
  • English
  • Français

A MODIFIED IMMERSED FINITE VOLUME ELEMENT METHOD FOR ELLIPTIC INTERFACE PROBLEMS

Part of: Partial differential equations, boundary value problems

Published online by Cambridge University Press:  13 May 2020

Q. WANG Open the ORCID record for Q. WANG [Opens in a new window]  and
Z. ZHANG Open the ORCID record for Z. ZHANG [Opens in a new window]
Q. WANG
Affiliation:
College of Engineering, Nanjing Agricultural University, Nanjing210031, China email wangquanxiang163@163.com
Z. ZHANG*
Affiliation:
Jiangsu Key Laboratory for NSLSCS, School of Mathematical Sciences, Nanjing Normal University, Nanjing210023, China email zhangzhiyue@njnu.edu.cn
*
✉zhangzhiyue@njnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents a new immersed finite volume element method for solving second-order elliptic problems with discontinuous diffusion coefficient on a Cartesian mesh. The new method possesses the local conservation property of classic finite volume element method, and it can overcome the oscillating behaviour of the classic immersed finite volume element method. The idea of this method is to reconstruct the control volume according to the interface, which makes it easy to implement. Optimal error estimates can be derived with respect to an energy norm under piecewise 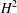$H^{2}$ regularity. Numerical results show that the new method significantly outperforms the classic immersed finite volume element method, and has second-order convergence in 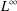$L^{\infty }$ norm.

Keywords

modifiedcontrol volumeinterface problemsCartesian mesh

MSC classification

Primary: 65N08: Finite volume methods
Type
Research Article
Information
The ANZIAM Journal , Volume 62 , Issue 1 , January 2020 , pp. 42 - 61
Copyright
© 2020 Australian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

An, N., Yu, X., Chen, H. and Huang, H., “A partially penalty immersed Crouzeix–Raviart finite element method for interface problems”, J. Inequal. Appl. 2017 (2017) 1–29; doi:10.1186/s13660-017-1461-5.CrossRefGoogle ScholarPubMed
Barrett, J., Elliott, C. and Charles, M., “Fitted and unfitted finite-element methods for elliptic equations with smooth interfaces”, IMA J. Numer. Anal. 52 (1987) 283–300; doi:10.1093/imanum/7.3.283.CrossRefGoogle Scholar
Bramble, J. and King, J., “A finite element method for interface problems in domains with smooth boundaries and interfaces”, Adv. Comput. Math. 6 (1996) 109–138; doi:10.1007/BF02127700.CrossRefGoogle Scholar
Brattkus, K. and Meiron, D., “Numerical simulations of unsteady crystal growth”, SIAM J. Appl. Math. 52 (1992) 1303–1320; doi:10.1137/0152075.CrossRefGoogle Scholar
Büger, R., Ruiz-Baier, R. and Tian, C., “Stability analysis and finite volume element discretization for delay-driven spatio-temporal patterns in a predator–prey model”, Math. Comput. Simulation 132 (2017) 28–52; doi:10.1016/j.matcom.2016.06.002.CrossRefGoogle Scholar
Chen, Z. and Zou, J., “Finite element methods and their convergence for elliptic and parabolic interface problems”, Numer. Math. 79 (1998) 175–202; doi:10.1007/s002110050336.CrossRefGoogle Scholar
Chen, C., Liu, W. and Bi, C., “A two-grid characteristic finite volume element method for semilinear advection-dominated diffusion equations”, Numer. Methods Partial Differential Equations 29 (2013) 1543–1562; doi:10.1002/num.21766.CrossRefGoogle Scholar
Chou, S., Kwak, D. and Li, Q., “$L^{p}$ error estimates and super convergence for covolume or finite volume element methods”, Numer. Methods Partial Differential Equations 19 (2003) 463–486; doi:10.1002/num.10059.CrossRefGoogle Scholar
Chou, S. and Ye, X., “Unified analysis of finite volume methods for second order elliptic problems”, SIAM J. Numer. Anal. 45 (2007) 1639–1653; doi:10.1137/050643994.CrossRefGoogle Scholar
Ewing, R., Li, Z., Tao, L. and Lin, Y., “The immersed finite volume element methods for the elliptic interface problems”, Math. Comput. Simulation 50 (1999) 63–76; doi:10.1016/S0378-4754(99)00061-0.CrossRefGoogle Scholar
Ewing, R., Tao, L. and Lin, Y., “On the accuracy of the finite volume element method based on piecewise linear polynomials”, SIAM J. Numer. Anal. 39 (2002) 1865–1888; doi:10.1137/S0036142900368873.CrossRefGoogle Scholar
Fogelson, A., “A mathematical model and numerical method for studying platelet adhesion and aggregation during blood clotting”, J. Comput. Phys. 56 (1984) 111–134; doi:10.1016/0021-9991(84)90086-X.CrossRefGoogle Scholar
Gao, F. and Yuan, Y., “An upwind finite volume element method based on quadrilateral meshes for nonlinear convection-diffusion problems”, Numer. Methods Partial Differential Equations 25 (2009) 1067–1085; doi:10.1002/num.20387.CrossRefGoogle Scholar
Guo, R., Lin, T. and Zhang, X., “Nonconforming immersed finite element spaces for elliptic interface problems”, Comput. Math. Appl. 75 (2018) 2002–2016; doi:10.1016/j.camwa.2017.10.040.CrossRefGoogle Scholar
Hansbo, A. and Hansbo, P., “An unfitted finite element method, based on Nitsche’s method, for elliptic interface problems”, Comput. Methods Appl. Mech. Engrg. 47 (2002) 5537–5552; doi:10.1016/S0045-7825(02)00524-8.CrossRefGoogle Scholar
He, X., Lin, T. and Lin, Y., “A bilinear immersed finite volume element method for the diffusion equation with discontinuous coefficient”, Commun. Comput. Phys. 6 (2009) 185–202; doi:10.4208/cicp.2009.v6.p185.CrossRefGoogle Scholar
Huang, P., Wu, H. and Xiao, Y., “An unfitted interface penalty finite element method for elliptic interface problems”, Comput. Methods Appl. Mech. Engrg. 323 (2017) 439–460; doi:10.1016/j.cma.2017.06.004.CrossRefGoogle Scholar
Ito, K., Kunisch, K. and Li, Z., “Level-set function approach to an inverse interface problem”, Inverse Problems 17 (2001) 1225–1242; doi:10.1088/0266-5611/17/5/301.CrossRefGoogle Scholar
Ji, H., Chen, J. and Li, Z., “A symmetric and consistent immersed finite element method for interface problems”, J. Sci. Comput. 61 (2014) 533–557; doi:10.1007/s10915-014-9837-x.CrossRefGoogle Scholar
Kwak, D., Jin, S. and Kyeong, D., “A stabilized P1-nonconforming immersed finite element method for the interface elasticity problems”, ESAIM Math. Model. Numer. Anal. 51 (2017) 187–207; doi:10.1051/m2an/2016011.CrossRefGoogle Scholar
Kwak, D. and Lee, J., “A modified $P_{1}$ immersed finite element method”, J. Pure Appl. Math. 104 (2015) 471–494; doi:10.12732/ijpam.v104i3.14.Google Scholar
Kwak, D., Wee, K. and Chang, K., “An analysis of a broken P1-nonconforming finite element method for interface problems”, SIAM J. Numer. Anal. 48 (2010) 2117–2134; doi:10.1137/080728056.CrossRefGoogle Scholar
Lamichhane, B. and Wohlmuth, B., “Mortar finite elements for interface problems”, Computing 72 (2004) 333–348; doi:10.1007/s00607-003-0062-y.CrossRefGoogle Scholar
LeVeque, R. and Li, Z., “The immersed interface method for elliptic equations with discontinuous coefficients and singular sources”, SIAM J. Numer. Anal. 31 (1994) 1019–1044; doi:10.1137/0731054.CrossRefGoogle Scholar
Li, R., Chen, Z. and Wu, W., Generalized difference methods for differential equations: numerical analysis of finite volume methods (Dekker, New York, 2000); doi:10.1201/9781482270211.CrossRefGoogle Scholar
Li, Z., Lin, T., Lin, Y. and Rogers, R., “An immersed finite element space and its approximation capability”, Numer. Methods Partial Differential Equations 20 (2004) 338–367; doi:10.1002/num.10092.CrossRefGoogle Scholar
Li, Z., Lin, T. and Wu, X., “New Cartesian grid methods for interface problems using the finite element formulation”, Numer. Math. 96 (2003) 61–98; doi:10.1007/s00211-003-0473-x.CrossRefGoogle Scholar
Lin, T., Lin, Y. and Zhang, X., “A method of lines based on immersed finite elements for parabolic moving interface problems”, Adv. Appl. Math. Mech. 5 (2013) 548–568; doi:10.4208/aamm.13-13S11.CrossRefGoogle Scholar
Lin, T., Lin, Y. and Zhang, X., “Partially penalized immersed finite element methods for elliptic interface problems”, SIAM J. Numer. Anal. 53 (2015) 1121–1144; doi:10.1137/130912700.CrossRefGoogle Scholar
Lin, T., Sheen, D. and Zhang, X., “A nonconforming immersed finite element method for elliptic interface problems”, J. Sci. Comput. 79 (2019) 442–463; doi:10.1007/s10915-018-0865-9.CrossRefGoogle Scholar
Lin, T. and Zhang, X., “Linear and bilinear immersed finite elements for planar elasticity interface problems”, J. Comput. Appl. Math. 236 (2012) 4681–4699; doi:10.1016/j.cam.2012.03.012.CrossRefGoogle Scholar
Peskin, C., “Flow patterns around heart valves: a numerical method”, J. Comput. Phys. 10 (1972) 252–271; doi:10.1016/0021-9991(72)90065-4.CrossRefGoogle Scholar
Peskin, C., “Numerical analysis of blood flow in the heart”, J. Comput. Phys. 25 (1977) 220–252; doi:10.1016/0021-9991(77)90100-0.CrossRefGoogle Scholar
Unverdi, S. and Tryggvason, G., “A front-tracking method for viscous, incompressible, multi-fluid flows”, J. Comput. Phys. 100 (1992) 25–37; doi:10.1016/0021-9991(92)90307-K.CrossRefGoogle Scholar
Wang, H., Chen, J., Sun, P. and Wang, N., “A conforming enriched finite element method for Stokes interface problems”, Comput. Math. Appl. 75 (2018) 4256–4271; doi:10.1016/j.camwa.2018.03.027.CrossRefGoogle Scholar
Wang, Q. and Zhang, Z., “A stabilized immersed finite volume element method for elliptic interface problems”, Appl. Numer. Math. 143 (2019) 75–87; doi:10.1016/j.apnum.2019.03.010.CrossRefGoogle Scholar
Wang, Q., Zhang, Z. and Li, Z., “A Fourier finite volume element method for solving two-dimensional quasi-geostrophic equations on a sphere”, Appl. Numer. Math. 71 (2013) 1–13; doi:10.1016/j.apnum.2013.03.007.CrossRefGoogle Scholar
Wang, Q., Zhang, Z., Zhang, X. and Zhu, Q., “Energy-preserving finite volume element method for the improved Boussinesq equation”, J. Comput. Phys. 270 (2014) 58–69; doi:10.1016/j.jcp.2014.03.053.CrossRefGoogle Scholar
Wang, T., “Alternating direction finite volume element methods for 2D parabolic partial differential equations”, Numer. Methods Partial Differential Equations 24 (2008) 24–40; doi:10.1002/num.20224.CrossRefGoogle Scholar
Wang, X. and Li, Y., “$L^{2}$ Error estimates for high order finite volume methods on triangular meshes”, SIAM J. Numer. Anal. 54 (2016) 2729–2749; doi:10.1137/140988486.CrossRefGoogle Scholar
Zhu, L., Zhang, Z. and Li, Z., “An immersed finite volume element method for 2D PDEs with discontinuous coefficients and non-homogeneous jump conditions”, Comput. Math. Appl. 70 (2015) 89–103; doi:10.1016/j.camwa.2015.04.012.CrossRefGoogle Scholar