Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-19T05:07:46.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Polylogarithmic bounds in the nilpotent Freiman theorem

Part of: Sequences and sets Additive number theory; partitions

Published online by Cambridge University Press:  08 October 2019

MATTHEW C. H. TOINTON
MATTHEW C. H. TOINTON*
Affiliation:
Pembroke College, Cambridge, CB2 1RF. e-mail: mcht2@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that if A is a finite K-approximate subgroup of an s-step nilpotent group then there is a finite normal subgroup 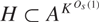$H \subset {A^{{K^{{O_s}(1)}}}}$ modulo which 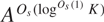${A^{{O_s}(\mathop {\log }\nolimits^{{O_s}(1)} K)}}$ contains a nilprogression of rank at most 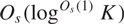${O_s}(\mathop {\log }\nolimits^{{O_s}(1)} K)$ and size at least 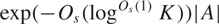$\exp ( - {O_s}(\mathop {\log }\nolimits^{{O_s}(1)} K))|A|$. This partially generalises the close-to-optimal bounds obtained in the abelian case by Sanders, and improves the bounds and simplifies the exposition of an earlier result of the author. Combined with results of Breuillard–Green, Breuillard–Green–Tao, Gill–Helfgott–Pyber–Szabó, and the author, this leads to improved rank bounds in Freiman-type theorems in residually nilpotent groups and certain linear groups of bounded degree.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11P70: Inverse problems of additive number theory, including sumsets
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 170 , Issue 1 , January 2021 , pp. 111 - 127
Copyright
© Cambridge Philosophical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The author is the Stokes Research Fellow at Pembroke College, Cambridge.

References

REFERENCES

Breuillard, E. and Green, B. J.. Approximate groups, I: the torsion-free nilpotent case. J. Inst. Math. Jussieu 10(1) (2011), 37–57.CrossRefGoogle Scholar
Breuillard, E. and Green, B. J.. Approximate groups, II: the solvable linear case. Q. J. Math. 62(3) (2011), 513–521.CrossRefGoogle Scholar
Breuillard, E., Green, B. J. and Tao, T. C.. Approximate subgroups of linear groups. Geom. Funct. Anal. 21(4) (2011), 774–819.CrossRefGoogle Scholar
Breuillard, E., Green, B. J. and Tao, T. C.. The structure of approximate groups. Publ. Math. IHES. 116(1) (2012), 115–221.CrossRefGoogle Scholar
Breuillard, E., Green, B. J. and Tao, T. C.. Small doubling in groups. Proc. Erdös Centenery Conference (2013); arXiv:1301.7718.Google Scholar
Breuillard, E. and Tointon, M. C. H.. Nilprogressions and groups with moderate growth. Adv. Math. 289 (2016), 1008–1055.CrossRefGoogle Scholar
Chang, M. C.. A polynomial bound in Freiman’s theorem. Duke Math. J . 113(3) (2002), 399–419.CrossRefGoogle Scholar
Freiman, G. A.. Foundations of a structural theory of set addition. Trans. of Math. Monogr. 37 (Amer. Math. Soc., Providence, RI 1973). Translated from the 1966 Russian version, published by Kazan Gos. Ped. Inst.Google Scholar
Gill, N. and Helfgott, H. A.. Growth in solvable subgroups of GL r (ℤ/pℤ). Math. Ann. 360(1) (2014), 157–208.CrossRefGoogle Scholar
Green, B. J.. Approximate groups and their applications: work of Bourgain, Gamburd, Helfgott and Sarnak. Current events bulletin of the AMS (2010), arXiv:0911.3354.Google Scholar
Green, B. J.. Approximate algebraic structure. Proc. ICM 2014 vol. 1, 341–367.Google Scholar
Green, B. J. and Ruzsa, I. Z.. Freiman’s theorem in an arbitrary abelian group. J. Lond. Math. Soc. 75(1) (2007), 163–175.CrossRefGoogle Scholar
Hall, M.. The theory of groups. Amer. Math. Soc./Chelsea, Providence, RI (1999).Google Scholar
Helfgott, H. A.. Growth in groups: ideas and perspectives. Bull. Amer. Math. Soc. 52 (2015), 357–413.CrossRefGoogle Scholar
Mal’cev, A. I.. On certain classes of infinite soluble groups. Mat. Sb. 28 (1951), 567–588 (in Russian), Amer. Math. Soc. Transl. 45(2) (1956), 1–21.Google Scholar
Petridis, G.. New proofs of Plünnecke-type estimates for product sets in groups. Combinatorica 32(6) (2012), 721–733.CrossRefGoogle Scholar
Ruzsa, I. Z.. An analog of Freiman’s theorem in groups, Structure theory of set addition. Astérisque 258 (1999), 323–326.Google Scholar
Sanders, T.. On the Bogolyubov–Ruzsa lemma. Anal. PDE 5(3) (2012), 627–655.CrossRefGoogle Scholar
Sanders, T.. The structure theory of set addition revisited. Bull. Amer. Math. Soc. 50 (2013), 93–127.CrossRefGoogle Scholar
Schoen, T.. Near optimal bounds in Freiman’s theorem. Duke Math. J . 158 (2011), 1–12.CrossRefGoogle Scholar
Tao, T. C.. Product set estimates for non-commutative groups. Combinatorica 28(5) (2008), 547–594.CrossRefGoogle Scholar
Tao, T. C.. Inverse theorems for sets and measures of polynomial growth. Q. J. Math. 68(1) (2017), 13–57.Google Scholar
Tessera, R. and Tointon, M. C. H.. Properness of nilprogressions and the persistence of polynomial growth of given degree. Discrete Anal . 17 (2018), 38 pp.Google Scholar
Tointon, M. C. H.. Freiman’s theorem in an arbitrary nilpotent group. Proc. London Math. Soc. 109 (2014), 318–352.CrossRefGoogle Scholar
Tointon, M. C. H.. Approximate subgroups of residually nilpotent groups. Math. Ann. 374 (2019), 499–515.CrossRefGoogle ScholarPubMed
Tointon, M. C. H.. Raconte-moi… les groupes approximatifs. Gaz. Math. 160 (2019), 53–59.Google Scholar
Tointon, M. C. H.. Introduction to approximate groups. London Mathematical Society Student Texts 94 (Cambridge University Press, Cambridge, 2020).Google Scholar
Wehrfritz, B. A. F.. Infinite Linear Groups (Springer-Verlag, Berlin, 1973).CrossRefGoogle Scholar