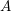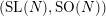1 Introduction
In this paper we consider the Springer correspondence in the case of symmetric spaces. We will concentrate on the split case of type
![]() $A$
, i.e., the case of
$A$
, i.e., the case of
![]() $\text{SL}(n,\mathbb{R})$
. The case of
$\text{SL}(n,\mathbb{R})$
. The case of
![]() $\text{SL}(n,\mathbb{H})$
was considered by Henderson in [Reference HendersonHen01], Grinberg in [Reference GrinbergGri98] and Lusztig in [Reference LusztigLus11a], and the case of
$\text{SL}(n,\mathbb{H})$
was considered by Henderson in [Reference HendersonHen01], Grinberg in [Reference GrinbergGri98] and Lusztig in [Reference LusztigLus11a], and the case of
![]() $\text{U}(p,q)$
was considered by Lusztig in [Reference LusztigLus11b] where he treats the general case of semisimple inner automorphisms. In both of these cases Springer theory closely resembles the classical situation. This turns out not to be so in the split case we consider here. In [Reference Chen, Vilonen and XueCVX15a, Reference Chen, Vilonen and XueCVX15b] we have computed Fourier transforms of IC sheaves supported on certain nilpotent orbits using resolutions of singularities of nilpotent orbit closures. In this paper we study the problem in general in the split case of type
$\text{U}(p,q)$
was considered by Lusztig in [Reference LusztigLus11b] where he treats the general case of semisimple inner automorphisms. In both of these cases Springer theory closely resembles the classical situation. This turns out not to be so in the split case we consider here. In [Reference Chen, Vilonen and XueCVX15a, Reference Chen, Vilonen and XueCVX15b] we have computed Fourier transforms of IC sheaves supported on certain nilpotent orbits using resolutions of singularities of nilpotent orbit closures. In this paper we study the problem in general in the split case of type
![]() $A$
replacing the resolutions with a nearby cycle sheaf construction in [Reference Grinberg, Vilonen and XueGVX18] based on earlier ideas of Grinberg [Reference GrinbergGri01, Reference GrinbergGri98].
$A$
replacing the resolutions with a nearby cycle sheaf construction in [Reference Grinberg, Vilonen and XueGVX18] based on earlier ideas of Grinberg [Reference GrinbergGri01, Reference GrinbergGri98].
Let us call an irreducible IC sheaf supported on a nilpotent orbit a nilpotent orbital complex. We show that the Fourier transform gives a bijection between nilpotent orbital complexes and certain representations of (extended) braid groups. We identify these representations of (extended) braid groups and construct them explicitly in terms of irreducible representations of Hecke algebras of symmetric groups at
![]() $q=-1$
. This bijection can be viewed as Springer correspondence for the symmetric pair
$q=-1$
. This bijection can be viewed as Springer correspondence for the symmetric pair
![]() $(\text{SL}(N),\text{SO}(N))$
. Let us note that the fact that representations of (affine) Hecke algebras at
$(\text{SL}(N),\text{SO}(N))$
. Let us note that the fact that representations of (affine) Hecke algebras at
![]() $q=-1$
arise in this situation was already observed by Grojnowski in his thesis [Reference GrojnowskiGro92].
$q=-1$
arise in this situation was already observed by Grojnowski in his thesis [Reference GrojnowskiGro92].
The proof of our main result, Theorem 4.1, makes use of a nearby cycle sheaf construction in [Reference Grinberg, Vilonen and XueGVX18] and smallness property of maps associated to certain
![]() $\unicode[STIX]{x1D703}$
-stable parabolic subgroups. The nearby cycle sheaves produce nilpotent orbital complexes whose Fourier transforms have full support. Those IC sheaves behave like ‘cuspidal sheaves’ in the sense that they do not appear as direct summands of parabolic inductions. On the other hand, the smallness property mentioned above implies a simple description of the images of parabolic induction functors (Propositions 3.1, 3.2). Those results together with a counting lemma (Lemma 4.2) imply Theorem 4.1. As corollaries, we obtain criteria for nilpotent orbital complexes to have full support Fourier transforms (Corollaries 4.8, 4.9) and results on cohomology of Hessenberg varieties (Theorem 5.2).
$\unicode[STIX]{x1D703}$
-stable parabolic subgroups. The nearby cycle sheaves produce nilpotent orbital complexes whose Fourier transforms have full support. Those IC sheaves behave like ‘cuspidal sheaves’ in the sense that they do not appear as direct summands of parabolic inductions. On the other hand, the smallness property mentioned above implies a simple description of the images of parabolic induction functors (Propositions 3.1, 3.2). Those results together with a counting lemma (Lemma 4.2) imply Theorem 4.1. As corollaries, we obtain criteria for nilpotent orbital complexes to have full support Fourier transforms (Corollaries 4.8, 4.9) and results on cohomology of Hessenberg varieties (Theorem 5.2).
Our method appears to be applicable to general symmetric pairs and, more generally, polar representations studied in [Reference GrinbergGri98] and we hope to return to this in future work.
Let us mention that in [Reference Lusztig and YunLY17], the authors show that one can obtain all nilpotent orbital complexes using spiral induction functors introduced in [Reference Lusztig and YunLY17] (in fact, they consider more general setting of cyclically graded Lie algebras). Using their results and Theorem 4.1, we show that all irreducible representations of Hecke algebras of symmetric groups at
![]() $q=-1$
appear in the intersection cohomology of Hessenberg varieties, with coefficient in certain local systems (see Theorem 6.3). This gives geometric constructions of irreducible representations of Hecke algebras of symmetric groups at
$q=-1$
appear in the intersection cohomology of Hessenberg varieties, with coefficient in certain local systems (see Theorem 6.3). This gives geometric constructions of irreducible representations of Hecke algebras of symmetric groups at
![]() $q=-1$
and provides them with a Hodge structure.
$q=-1$
and provides them with a Hodge structure.
The paper is organized as follows. In § 2 we recall some facts about symmetric pairs and introduce a class of representations of equivariant fundamental groups. Moreover, we recall the definition of the parabolic induction functor. In § 3 we study parabolic induction functors for certain
![]() $\unicode[STIX]{x1D703}$
-stable parabolic subgroups. In § 4, we prove Theorem 4.1: the Fourier transform defines a bijection between the set of nilpotent orbital complexes and the class of representations of equivariant fundamental groups introduced in § 2. In §§5 and 6, we discuss applications of our results to cohomology of Hessenberg varieties and representations of Hecke algebras of symmetric groups at
$\unicode[STIX]{x1D703}$
-stable parabolic subgroups. In § 4, we prove Theorem 4.1: the Fourier transform defines a bijection between the set of nilpotent orbital complexes and the class of representations of equivariant fundamental groups introduced in § 2. In §§5 and 6, we discuss applications of our results to cohomology of Hessenberg varieties and representations of Hecke algebras of symmetric groups at
![]() $q=-1$
. Finally, in § 7, we propose a conjecture that gives a more precise description of the bijection in Theorem 4.1.
$q=-1$
. Finally, in § 7, we propose a conjecture that gives a more precise description of the bijection in Theorem 4.1.
2 Preliminaries
For convenience we work over
![]() $\mathbb{C}$
. We adopt the usual convention of cohomological degrees for perverse sheaves by having them be symmetric around 0. We also use the convention that all functors are derived, so we write, for example,
$\mathbb{C}$
. We adopt the usual convention of cohomological degrees for perverse sheaves by having them be symmetric around 0. We also use the convention that all functors are derived, so we write, for example,
![]() $\unicode[STIX]{x1D70B}_{\ast }$
instead of
$\unicode[STIX]{x1D70B}_{\ast }$
instead of
![]() $R\unicode[STIX]{x1D70B}_{\ast }$
. If
$R\unicode[STIX]{x1D70B}_{\ast }$
. If
![]() $X$
is smooth we write
$X$
is smooth we write
![]() $\mathbb{C}_{X}[-]$
for the constant sheaf placed in degree
$\mathbb{C}_{X}[-]$
for the constant sheaf placed in degree
![]() $-\dim X$
so that
$-\dim X$
so that
![]() $\mathbb{C}_{X}[-]$
is perverse. If
$\mathbb{C}_{X}[-]$
is perverse. If
![]() $U\subset X$
is a smooth open dense subset of a variety
$U\subset X$
is a smooth open dense subset of a variety
![]() $X$
and
$X$
and
![]() ${\mathcal{L}}$
is a local system on
${\mathcal{L}}$
is a local system on
![]() $U$
, we write
$U$
, we write
![]() $\operatorname{IC}(X,{\mathcal{L}})$
for the IC-extension of
$\operatorname{IC}(X,{\mathcal{L}})$
for the IC-extension of
![]() ${\mathcal{L}}[-]$
to
${\mathcal{L}}[-]$
to
![]() $X$
; in particular, it is perverse. For simplicity of notation, when we have a pair
$X$
; in particular, it is perverse. For simplicity of notation, when we have a pair
![]() $({\mathcal{O}},{\mathcal{E}})$
, where
$({\mathcal{O}},{\mathcal{E}})$
, where
![]() ${\mathcal{O}}$
is an orbit and
${\mathcal{O}}$
is an orbit and
![]() ${\mathcal{E}}$
is a local system on
${\mathcal{E}}$
is a local system on
![]() ${\mathcal{O}}$
, we also write
${\mathcal{O}}$
, we also write
![]() $\operatorname{IC}({\mathcal{O}},{\mathcal{E}})$
instead of
$\operatorname{IC}({\mathcal{O}},{\mathcal{E}})$
instead of
![]() $\operatorname{IC}(\bar{{\mathcal{O}}},{\mathcal{E}})$
.
$\operatorname{IC}(\bar{{\mathcal{O}}},{\mathcal{E}})$
.
2.1 Notation
For
![]() $e\geqslant 2$
, a partition
$e\geqslant 2$
, a partition
![]() $\unicode[STIX]{x1D706}$
of a positive integer
$\unicode[STIX]{x1D706}$
of a positive integer
![]() $k$
is called
$k$
is called
![]() $e$
-regular if the multiplicity of any part of
$e$
-regular if the multiplicity of any part of
![]() $\unicode[STIX]{x1D706}$
is less than
$\unicode[STIX]{x1D706}$
is less than
![]() $e$
. In particular, a partition is
$e$
. In particular, a partition is
![]() $2$
-regular if and only if it has distinct parts. Let us denote by
$2$
-regular if and only if it has distinct parts. Let us denote by
![]() ${\mathcal{P}}(k)$
the set of all partitions of
${\mathcal{P}}(k)$
the set of all partitions of
![]() $k$
and by
$k$
and by
![]() ${\mathcal{P}}_{2}(k)$
the set of all
${\mathcal{P}}_{2}(k)$
the set of all
![]() $2$
-regular partitions of
$2$
-regular partitions of
![]() $k$
.
$k$
.
We denote by
![]() ${\mathcal{H}}_{k,-1}$
the Hecke algebra of the symmetric group
${\mathcal{H}}_{k,-1}$
the Hecke algebra of the symmetric group
![]() $S_{k}$
with parameter
$S_{k}$
with parameter
![]() $-1$
. More precisely,
$-1$
. More precisely,
![]() ${\mathcal{H}}_{k,-1}$
is the
${\mathcal{H}}_{k,-1}$
is the
![]() $\mathbb{C}$
-algebra generated by
$\mathbb{C}$
-algebra generated by
![]() $T_{i},~i=1,\ldots ,k-1$
, with the following relations
$T_{i},~i=1,\ldots ,k-1$
, with the following relations
It is shown in [Reference Dipper and JamesDJ86] that the set of isomorphism classes of irreducible representations of
![]() ${\mathcal{H}}_{k,-1}$
is parametrized by
${\mathcal{H}}_{k,-1}$
is parametrized by
![]() ${\mathcal{P}}_{2}(k)$
. For
${\mathcal{P}}_{2}(k)$
. For
![]() $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{2}(k)$
, we write
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{2}(k)$
, we write
![]() $D_{\unicode[STIX]{x1D707}}$
for the irreducible representation of
$D_{\unicode[STIX]{x1D707}}$
for the irreducible representation of
![]() ${\mathcal{H}}_{k,-1}$
corresponding to
${\mathcal{H}}_{k,-1}$
corresponding to
![]() $\unicode[STIX]{x1D707}$
.
$\unicode[STIX]{x1D707}$
.
For a real number
![]() $a$
, we write
$a$
, we write
![]() $[a]$
for its integer part.
$[a]$
for its integer part.
2.2 The split symmetric pair
 $(\text{SL}(N),\text{SO}(N))$
$(\text{SL}(N),\text{SO}(N))$
Let
![]() $G=\text{SL}(N)$
and
$G=\text{SL}(N)$
and
![]() $\unicode[STIX]{x1D703}:G\rightarrow G$
an involution such that
$\unicode[STIX]{x1D703}:G\rightarrow G$
an involution such that
![]() $K=G^{\unicode[STIX]{x1D703}}=\text{SO}(N)$
and write
$K=G^{\unicode[STIX]{x1D703}}=\text{SO}(N)$
and write
![]() $\mathfrak{g}=\operatorname{Lie}G$
. We have
$\mathfrak{g}=\operatorname{Lie}G$
. We have
![]() $\mathfrak{g}=\mathfrak{g}_{0}\oplus \mathfrak{g}_{1}$
, where
$\mathfrak{g}=\mathfrak{g}_{0}\oplus \mathfrak{g}_{1}$
, where
![]() $\unicode[STIX]{x1D703}|_{\mathfrak{g}_{i}}=(-1)^{i}$
. The pair
$\unicode[STIX]{x1D703}|_{\mathfrak{g}_{i}}=(-1)^{i}$
. The pair
![]() $(G,K)$
is a split symmetric pair, i.e., there exists a maximal torus
$(G,K)$
is a split symmetric pair, i.e., there exists a maximal torus
![]() $A$
of
$A$
of
![]() $G$
that is
$G$
that is
![]() $\unicode[STIX]{x1D703}$
-split, where
$\unicode[STIX]{x1D703}$
-split, where
![]() $\unicode[STIX]{x1D703}$
-split means that for all
$\unicode[STIX]{x1D703}$
-split means that for all
![]() $x\in A$
,
$x\in A$
,
![]() $\unicode[STIX]{x1D703}(x)=x^{-1}$
. We also think of the pair
$\unicode[STIX]{x1D703}(x)=x^{-1}$
. We also think of the pair
![]() $(G,K)$
concretely as
$(G,K)$
concretely as
![]() $(\text{SL}(V),\text{SO}(V))$
, where
$(\text{SL}(V),\text{SO}(V))$
, where
![]() $V$
is a vector space of dimension
$V$
is a vector space of dimension
![]() $N$
equipped with a non-degenerate quadratic form
$N$
equipped with a non-degenerate quadratic form
![]() $Q$
such that
$Q$
such that
![]() $\text{SO}(V)=\text{SO}(V,Q)$
. We write the non-degenerate bilinear form associated to
$\text{SO}(V)=\text{SO}(V,Q)$
. We write the non-degenerate bilinear form associated to
![]() $Q$
as
$Q$
as
![]() $\langle ~,\,\rangle$
.
$\langle ~,\,\rangle$
.
Let
![]() $\mathfrak{g}^{\text{rs}}$
denote the set of regular semisimple elements in
$\mathfrak{g}^{\text{rs}}$
denote the set of regular semisimple elements in
![]() $\mathfrak{g}$
and let
$\mathfrak{g}$
and let
![]() $\mathfrak{g}_{1}^{\text{rs}}=\mathfrak{g}_{1}\cap \mathfrak{g}^{\text{rs}}$
. Similarly, let
$\mathfrak{g}_{1}^{\text{rs}}=\mathfrak{g}_{1}\cap \mathfrak{g}^{\text{rs}}$
. Similarly, let
![]() $\mathfrak{g}^{\text{reg}}$
denote the set of regular elements in
$\mathfrak{g}^{\text{reg}}$
denote the set of regular elements in
![]() $\mathfrak{g}$
and let
$\mathfrak{g}$
and let
![]() $\mathfrak{g}_{1}^{\text{reg}}=\mathfrak{g}_{1}\cap \mathfrak{g}^{\text{reg}}$
.
$\mathfrak{g}_{1}^{\text{reg}}=\mathfrak{g}_{1}\cap \mathfrak{g}^{\text{reg}}$
.
Let
![]() ${\mathcal{N}}$
be the nilpotent cone of
${\mathcal{N}}$
be the nilpotent cone of
![]() $\mathfrak{g}$
and let
$\mathfrak{g}$
and let
![]() ${\mathcal{N}}_{1}={\mathcal{N}}\cap \mathfrak{g}$
. When
${\mathcal{N}}_{1}={\mathcal{N}}\cap \mathfrak{g}$
. When
![]() $N$
is odd, the set of
$N$
is odd, the set of
![]() $K$
-orbits in
$K$
-orbits in
![]() ${\mathcal{N}}_{1}$
is parametrized by
${\mathcal{N}}_{1}$
is parametrized by
![]() ${\mathcal{P}}(N)$
. When
${\mathcal{P}}(N)$
. When
![]() $N$
is even, the set of
$N$
is even, the set of
![]() $\text{O}(N)$
-orbits in
$\text{O}(N)$
-orbits in
![]() ${\mathcal{N}}_{1}$
is parametrized by
${\mathcal{N}}_{1}$
is parametrized by
![]() ${\mathcal{P}}(N)$
, moreover, each
${\mathcal{P}}(N)$
, moreover, each
![]() $\text{O}(N)$
-orbit remains one
$\text{O}(N)$
-orbit remains one
![]() $K$
-orbit if
$K$
-orbit if
![]() $\unicode[STIX]{x1D706}$
has at least one odd part, and splits into two
$\unicode[STIX]{x1D706}$
has at least one odd part, and splits into two
![]() $K$
-orbits otherwise. For
$K$
-orbits otherwise. For
![]() $\unicode[STIX]{x1D706}\in {\mathcal{P}}(N)$
, we write
$\unicode[STIX]{x1D706}\in {\mathcal{P}}(N)$
, we write
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
for the corresponding nilpotent
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
for the corresponding nilpotent
![]() $K$
-orbit in
$K$
-orbit in
![]() ${\mathcal{N}}_{1}$
when
${\mathcal{N}}_{1}$
when
![]() $\unicode[STIX]{x1D706}$
has at least one odd part, and write
$\unicode[STIX]{x1D706}$
has at least one odd part, and write
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\text{I}}$
and
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\text{I}}$
and
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\text{II}}$
for the corresponding two nilpotent
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\text{II}}$
for the corresponding two nilpotent
![]() $K$
-orbits in
$K$
-orbits in
![]() ${\mathcal{N}}_{1}$
when
${\mathcal{N}}_{1}$
when
![]() $\unicode[STIX]{x1D706}$
has only even parts. Suppose that
$\unicode[STIX]{x1D706}$
has only even parts. Suppose that
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{s}>0)$
. For
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{s}>0)$
. For
![]() $x\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(or
$x\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(or
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
), we have
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
), we have
Let
![]() $\mathfrak{a}$
be a maximal abelian subspace of
$\mathfrak{a}$
be a maximal abelian subspace of
![]() $\mathfrak{g}_{1}$
, which is also a Cartan subspace of
$\mathfrak{g}_{1}$
, which is also a Cartan subspace of
![]() $\mathfrak{g}$
. We have the ‘little’ Weyl group
$\mathfrak{g}$
. We have the ‘little’ Weyl group
2.3 Equivariant fundamental group and its representations
As was discussed in [Reference Chen, Vilonen and XueCVX15a], the equivariant fundamental group
where
![]() $B_{N}$
is the braid group of
$B_{N}$
is the braid group of
![]() $N$
strands and it acts on
$N$
strands and it acts on
via the natural map
![]() $B_{N}\rightarrow S_{N}$
. For simplicity we write
$B_{N}\rightarrow S_{N}$
. For simplicity we write
It is easy to see that the action of
![]() $B_{N}$
on
$B_{N}$
on
![]() $I_{N}^{\vee }$
has
$I_{N}^{\vee }$
has
![]() $[N/2]+1$
orbits. We choose a set of representatives
$[N/2]+1$
orbits. We choose a set of representatives
of the
![]() $B_{N}$
-orbits as follows. Let
$B_{N}$
-orbits as follows. Let
![]() $\unicode[STIX]{x1D70F}_{i}^{\prime }\in (\mathbb{Z}/2\mathbb{Z})^{N}$
be the element with all entries 0 except the
$\unicode[STIX]{x1D70F}_{i}^{\prime }\in (\mathbb{Z}/2\mathbb{Z})^{N}$
be the element with all entries 0 except the
![]() $i$
th position. Then
$i$
th position. Then
![]() $\{\unicode[STIX]{x1D70F}_{i}=\unicode[STIX]{x1D70F}_{i}^{\prime }+\unicode[STIX]{x1D70F}_{i+1}^{\prime },~i=1,\ldots ,N-1\}$
, is a set of generators for
$\{\unicode[STIX]{x1D70F}_{i}=\unicode[STIX]{x1D70F}_{i}^{\prime }+\unicode[STIX]{x1D70F}_{i+1}^{\prime },~i=1,\ldots ,N-1\}$
, is a set of generators for
![]() $I_{N}$
. For
$I_{N}$
. For
![]() $0\leqslant m\leqslant [N/2]$
, we define a character
$0\leqslant m\leqslant [N/2]$
, we define a character
![]() $\unicode[STIX]{x1D712}_{m}$
as follows:
$\unicode[STIX]{x1D712}_{m}$
as follows:
For
![]() $\unicode[STIX]{x1D712}\in I_{N}^{\vee }$
, we set
$\unicode[STIX]{x1D712}\in I_{N}^{\vee }$
, we set
Let
![]() $s_{i}$
,
$s_{i}$
,
![]() $i=1,\ldots ,N-1$
, be the simple reflections in
$i=1,\ldots ,N-1$
, be the simple reflections in
![]() $W=S_{N}$
. It is easy to check that
$W=S_{N}$
. It is easy to check that
Let us define
Then it follows from (2.4) that
Let
![]() $\unicode[STIX]{x1D70E}_{i},i=1,\ldots ,N-1$
, be the standard generators of
$\unicode[STIX]{x1D70E}_{i},i=1,\ldots ,N-1$
, be the standard generators of
![]() $B_{N}$
which are lifts of the
$B_{N}$
which are lifts of the
![]() $s_{i}$
under the map
$s_{i}$
under the map
![]() $B_{N}\rightarrow S_{N}$
. Then
$B_{N}\rightarrow S_{N}$
. Then
![]() $B_{m,N-m}$
is generated by
$B_{m,N-m}$
is generated by
![]() $\unicode[STIX]{x1D70E}_{i}$
,
$\unicode[STIX]{x1D70E}_{i}$
,
![]() $i\neq m$
, and
$i\neq m$
, and
![]() $\unicode[STIX]{x1D70E}_{m}^{2}$
. We have a natural quotient map
$\unicode[STIX]{x1D70E}_{m}^{2}$
. We have a natural quotient map
Note that in the above formula the
![]() $\unicode[STIX]{x1D70E}_{i}$
corresponds to
$\unicode[STIX]{x1D70E}_{i}$
corresponds to
![]() $-T_{i}$
of the Hecke algebra in (2.1). For us the
$-T_{i}$
of the Hecke algebra in (2.1). For us the
![]() $\unicode[STIX]{x1D70E}_{i}$
are more natural generators since they arise from geometry as unipotent monodromy operators.
$\unicode[STIX]{x1D70E}_{i}$
are more natural generators since they arise from geometry as unipotent monodromy operators.
Let us write
We consider a family of representations of
![]() $\widetilde{B}_{N}$
as follows. For
$\widetilde{B}_{N}$
as follows. For
![]() $0\leqslant m\leqslant [N/2]$
, we define
$0\leqslant m\leqslant [N/2]$
, we define
where in the tensor product
![]() $\mathbb{C}[B_{m,N-m}]$
acts on
$\mathbb{C}[B_{m,N-m}]$
acts on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
via the quotient map (2.6) and on
${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
via the quotient map (2.6) and on
![]() $\mathbb{C}[B_{N}]$
by right multiplication. The module
$\mathbb{C}[B_{N}]$
by right multiplication. The module
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
has a natural
$L_{\unicode[STIX]{x1D712}_{m}}$
has a natural
![]() $\widetilde{B}_{N}$
-action defined as follows. We let
$\widetilde{B}_{N}$
-action defined as follows. We let
![]() $B_{N}$
act on
$B_{N}$
act on
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
by left multiplication and we let
$L_{\unicode[STIX]{x1D712}_{m}}$
by left multiplication and we let
![]() $I_{N}$
act on
$I_{N}$
act on
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
via
$L_{\unicode[STIX]{x1D712}_{m}}$
via
![]() $a.(b\otimes v)=((b.\unicode[STIX]{x1D712}_{m})(a))(b\otimes v)$
for
$a.(b\otimes v)=((b.\unicode[STIX]{x1D712}_{m})(a))(b\otimes v)$
for
![]() $a\in I_{N}$
,
$a\in I_{N}$
,
![]() $b\in B_{N}$
and
$b\in B_{N}$
and
![]() $v\in {\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
. We view
$v\in {\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
. We view
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
as a representation of the equivariant fundamental group
$L_{\unicode[STIX]{x1D712}_{m}}$
as a representation of the equivariant fundamental group
![]() $\widetilde{B}_{N}$
in this manner.
$\widetilde{B}_{N}$
in this manner.
We will next identify the composition factors of the modules
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
. Let
$L_{\unicode[STIX]{x1D712}_{m}}$
. Let
![]() $\unicode[STIX]{x1D707}^{1}\in {\mathcal{P}}_{2}(m)$
and
$\unicode[STIX]{x1D707}^{1}\in {\mathcal{P}}_{2}(m)$
and
![]() $\unicode[STIX]{x1D707}^{2}\in {\mathcal{P}}_{2}(N-m)$
,
$\unicode[STIX]{x1D707}^{2}\in {\mathcal{P}}_{2}(N-m)$
,
![]() $m\in [0,[N/2]]$
. Proceeding just as in the definition of
$m\in [0,[N/2]]$
. Proceeding just as in the definition of
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
, one obtains the following representation of
$L_{\unicode[STIX]{x1D712}_{m}}$
, one obtains the following representation of
![]() $\widetilde{B}_{N}$
:
$\widetilde{B}_{N}$
:
Using (2.5), one readily checks that
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
is an irreducible representation of
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
is an irreducible representation of
![]() $\widetilde{B}_{N}$
when
$\widetilde{B}_{N}$
when
![]() $m\neq N/2$
, or when
$m\neq N/2$
, or when
![]() $m=N/2$
and
$m=N/2$
and
![]() $\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2}$
. When
$\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2}$
. When
![]() $m=N/2$
and
$m=N/2$
and
![]() $\unicode[STIX]{x1D707}^{1}=\unicode[STIX]{x1D707}^{2}$
,
$\unicode[STIX]{x1D707}^{1}=\unicode[STIX]{x1D707}^{2}$
,
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
breaks into the direct sum of two non-isomorphic irreducible representations of
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
breaks into the direct sum of two non-isomorphic irreducible representations of
![]() $\widetilde{B}_{N}$
, which we denote by
$\widetilde{B}_{N}$
, which we denote by
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}^{\text{I}}$
and
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}^{\text{I}}$
and
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}^{\text{II}}$
, i.e., we have
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}^{\text{II}}$
, i.e., we have
Moreover,
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \text{when }m\neq N/2,~V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}\cong V_{\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2}}\quad \text{if and only if }(\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})=(\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2});\\ \displaystyle \text{when }m=N/2,~V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}\cong V_{\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2}}\quad \text{if and only if }\\ \displaystyle \text{either }(\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})=(\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2})\quad \text{or}\quad (\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})=(\unicode[STIX]{x1D708}^{2},\unicode[STIX]{x1D708}^{1}).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \text{when }m\neq N/2,~V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}\cong V_{\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2}}\quad \text{if and only if }(\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})=(\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2});\\ \displaystyle \text{when }m=N/2,~V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}\cong V_{\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2}}\quad \text{if and only if }\\ \displaystyle \text{either }(\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})=(\unicode[STIX]{x1D708}^{1},\unicode[STIX]{x1D708}^{2})\quad \text{or}\quad (\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})=(\unicode[STIX]{x1D708}^{2},\unicode[STIX]{x1D708}^{1}).\end{array}\end{eqnarray}$$
As the
![]() $D_{\unicode[STIX]{x1D707}^{1}}\otimes D_{\unicode[STIX]{x1D707}^{2}}$
are the composition factors of
$D_{\unicode[STIX]{x1D707}^{1}}\otimes D_{\unicode[STIX]{x1D707}^{2}}$
are the composition factors of
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
we conclude the following.
${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
we conclude the following.
Lemma 2.1. The composition factors of
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
consist of the
$L_{\unicode[STIX]{x1D712}_{m}}$
consist of the
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
,
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
,
![]() $\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2}$
,
$\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2}$
,
![]() $\unicode[STIX]{x1D707}^{1}\in {\mathcal{P}}_{2}(m)$
,
$\unicode[STIX]{x1D707}^{1}\in {\mathcal{P}}_{2}(m)$
,
![]() $\unicode[STIX]{x1D707}^{2}\in {\mathcal{P}}_{2}(N-m)$
, and when
$\unicode[STIX]{x1D707}^{2}\in {\mathcal{P}}_{2}(N-m)$
, and when
![]() $N=2m$
we have two additional composition factors
$N=2m$
we have two additional composition factors
![]() $V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\text{I}}$
and
$V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\text{I}}$
and
![]() $V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\text{II}}$
for
$V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\text{II}}$
for
![]() $\unicode[STIX]{x1D707}\in {\mathcal{P}}_{2}(m)$
.
$\unicode[STIX]{x1D707}\in {\mathcal{P}}_{2}(m)$
.
2.4 Parabolic induction functor and Fourier transform
Let
![]() $L$
be a
$L$
be a
![]() $\unicode[STIX]{x1D703}$
-stable Levi subgroup contained in a
$\unicode[STIX]{x1D703}$
-stable Levi subgroup contained in a
![]() $\unicode[STIX]{x1D703}$
-stable parabolic subgroup
$\unicode[STIX]{x1D703}$
-stable parabolic subgroup
![]() $P\subset G$
. We write
$P\subset G$
. We write
We will make use of the parabolic induction functor
defined in [Reference HendersonHen01, Reference LusztigLus11b]. In the following we recall its definition. Let
be the natural projection map, where
![]() $\mathfrak{n}_{P}$
is the nilpotent radical of
$\mathfrak{n}_{P}$
is the nilpotent radical of
![]() $\mathfrak{p}$
and
$\mathfrak{p}$
and
![]() $(\mathfrak{n}_{P})_{1}=\mathfrak{n}_{P}\cap \mathfrak{g}_{1}$
. Consider the diagram
$(\mathfrak{n}_{P})_{1}=\mathfrak{n}_{P}\cap \mathfrak{g}_{1}$
. Consider the diagram
where
![]() $p_{1}$
and
$p_{1}$
and
![]() $p_{2}$
are natural projection maps and
$p_{2}$
are natural projection maps and
![]() $\check{\unicode[STIX]{x1D70B}}:(k,x)\mapsto \operatorname{Ad}(k)(x)$
.
$\check{\unicode[STIX]{x1D70B}}:(k,x)\mapsto \operatorname{Ad}(k)(x)$
.
The maps in (2.10) are
![]() $K\times P_{K}$
-equivariant, where
$K\times P_{K}$
-equivariant, where
![]() $K$
acts trivially on
$K$
acts trivially on
![]() $\mathfrak{l}_{1}$
and
$\mathfrak{l}_{1}$
and
![]() $\mathfrak{p}_{1}$
, by left multiplication on the
$\mathfrak{p}_{1}$
, by left multiplication on the
![]() $K$
-factor on
$K$
-factor on
![]() $K\times \mathfrak{p}_{1}$
and on
$K\times \mathfrak{p}_{1}$
and on
![]() $K\times ^{P_{K}}\mathfrak{p}_{1}$
, and by adjoint action on
$K\times ^{P_{K}}\mathfrak{p}_{1}$
, and by adjoint action on
![]() $\mathfrak{g}_{1}$
, and
$\mathfrak{g}_{1}$
, and
![]() $P_{K}$
acts on
$P_{K}$
acts on
![]() $\mathfrak{l}_{1}$
by
$\mathfrak{l}_{1}$
by
![]() $a.l=\operatorname{pr}(\operatorname{Ad}a(l))$
, by adjoint action on
$a.l=\operatorname{pr}(\operatorname{Ad}a(l))$
, by adjoint action on
![]() $\mathfrak{p}_{1}$
, by
$\mathfrak{p}_{1}$
, by
![]() $a.(k,p)=(ka^{-1},\operatorname{Ad}a(p))$
on
$a.(k,p)=(ka^{-1},\operatorname{Ad}a(p))$
on
![]() $K\times \mathfrak{p}_{1}$
, trivially on
$K\times \mathfrak{p}_{1}$
, trivially on
![]() $K\times ^{P_{K}}\mathfrak{p}_{1}$
and
$K\times ^{P_{K}}\mathfrak{p}_{1}$
and
![]() $\mathfrak{g}_{1}$
.
$\mathfrak{g}_{1}$
.
Let
![]() $A$
be a complex in
$A$
be a complex in
![]() $D_{L_{K}}(\mathfrak{l}_{1})$
. Then
$D_{L_{K}}(\mathfrak{l}_{1})$
. Then
![]() $(\operatorname{pr}\circ \,p_{1})^{\ast }A\cong p_{2}^{\ast }A^{\prime }$
for a well-defined complex
$(\operatorname{pr}\circ \,p_{1})^{\ast }A\cong p_{2}^{\ast }A^{\prime }$
for a well-defined complex
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $D_{K}(K\times ^{P_{K}}\mathfrak{p}_{1})$
. Define
$D_{K}(K\times ^{P_{K}}\mathfrak{p}_{1})$
. Define
Let
![]() $\mathfrak{F}:D_{K}(\mathfrak{g}_{1})\rightarrow D_{K}(\mathfrak{g}_{1})$
be the Fourier transform functor (we also use the same notation
$\mathfrak{F}:D_{K}(\mathfrak{g}_{1})\rightarrow D_{K}(\mathfrak{g}_{1})$
be the Fourier transform functor (we also use the same notation
![]() $\mathfrak{F}$
for the functor defined for
$\mathfrak{F}$
for the functor defined for
![]() $(L_{K},\mathfrak{l}_{1})$
). Here we have identified
$(L_{K},\mathfrak{l}_{1})$
). Here we have identified
![]() $\mathfrak{g}_{1}$
with
$\mathfrak{g}_{1}$
with
![]() $\mathfrak{g}_{1}^{\ast }$
via a
$\mathfrak{g}_{1}^{\ast }$
via a
![]() $K$
-invariant non-degenerate bilinear form on
$K$
-invariant non-degenerate bilinear form on
![]() $\mathfrak{g}_{1}$
. It is shown in [Reference HendersonHen01, Reference LusztigLus11b] that the induction functor commutes with Fourier transform, i.e.,
$\mathfrak{g}_{1}$
. It is shown in [Reference HendersonHen01, Reference LusztigLus11b] that the induction functor commutes with Fourier transform, i.e.,
3 Maximal
 $\unicode[STIX]{x1D703}$
-stable parabolic subgroups and parabolic induction
$\unicode[STIX]{x1D703}$
-stable parabolic subgroups and parabolic induction
In this section, we study the parabolic induction functor with respect to a chosen family of
![]() $L^{m}\subset P^{m}$
,
$L^{m}\subset P^{m}$
,
![]() $1\leqslant m<N/2$
, and two more pairs
$1\leqslant m<N/2$
, and two more pairs
![]() $L^{n,\unicode[STIX]{x1D714}}\subset P^{n,\unicode[STIX]{x1D714}}$
,
$L^{n,\unicode[STIX]{x1D714}}\subset P^{n,\unicode[STIX]{x1D714}}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
, if
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
, if
![]() $N=2n$
, where
$N=2n$
, where
![]() $P^{m}$
(respectively
$P^{m}$
(respectively
![]() $P^{n,\unicode[STIX]{x1D714}}$
) is a maximal
$P^{n,\unicode[STIX]{x1D714}}$
) is a maximal
![]() $\unicode[STIX]{x1D703}$
-stable parabolic subgroup and
$\unicode[STIX]{x1D703}$
-stable parabolic subgroup and
![]() $L^{m}$
(respectively
$L^{m}$
(respectively
![]() $L^{n,\unicode[STIX]{x1D714}}$
) is a
$L^{n,\unicode[STIX]{x1D714}}$
) is a
![]() $\unicode[STIX]{x1D703}$
-stable Levi subgroup of
$\unicode[STIX]{x1D703}$
-stable Levi subgroup of
![]() $P^{m}$
(respectively
$P^{m}$
(respectively
![]() $P^{n,\unicode[STIX]{x1D714}}$
) defined as follows.
$P^{n,\unicode[STIX]{x1D714}}$
) defined as follows.
Fix a basis
![]() $\{e_{i},1\leqslant i\leqslant N\}$
of
$\{e_{i},1\leqslant i\leqslant N\}$
of
![]() $V$
such that
$V$
such that
![]() $\langle e_{i},e_{j}\rangle =\unicode[STIX]{x1D6FF}_{i+j,N+1}$
. For
$\langle e_{i},e_{j}\rangle =\unicode[STIX]{x1D6FF}_{i+j,N+1}$
. For
![]() $1\leqslant m<N/2$
, we define
$1\leqslant m<N/2$
, we define
![]() $P^{m}$
to be the parabolic subgroup of
$P^{m}$
to be the parabolic subgroup of
![]() $G$
that stabilizes the flag
$G$
that stabilizes the flag
where
![]() $V_{m}^{0}=\operatorname{span}\{e_{i},1\leqslant i\leqslant m\}$
. We define
$V_{m}^{0}=\operatorname{span}\{e_{i},1\leqslant i\leqslant m\}$
. We define
![]() $L^{m}$
to be the
$L^{m}$
to be the
![]() $\unicode[STIX]{x1D703}$
-stable Levi subgroup of
$\unicode[STIX]{x1D703}$
-stable Levi subgroup of
![]() $P^{m}$
which consists of diagonal block matrices of sizes
$P^{m}$
which consists of diagonal block matrices of sizes
![]() $m,N-2m,m$
. When
$m,N-2m,m$
. When
![]() $N=2n$
, for
$N=2n$
, for
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
, we define
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
, we define
![]() $P^{n,\unicode[STIX]{x1D714}}$
to be the parabolic subgroup of
$P^{n,\unicode[STIX]{x1D714}}$
to be the parabolic subgroup of
![]() $G$
that stabilizes the flag
$G$
that stabilizes the flag
where
![]() $V_{n}^{\text{I}}=\operatorname{span}\{e_{i},1\leqslant i\leqslant n\}$
and
$V_{n}^{\text{I}}=\operatorname{span}\{e_{i},1\leqslant i\leqslant n\}$
and
![]() $V_{n}^{\text{II}}=\operatorname{span}\{e_{i},1\leqslant i\leqslant n-1,e_{n+1}\}$
. Let
$V_{n}^{\text{II}}=\operatorname{span}\{e_{i},1\leqslant i\leqslant n-1,e_{n+1}\}$
. Let
![]() $L^{n,\unicode[STIX]{x1D714}}$
be a
$L^{n,\unicode[STIX]{x1D714}}$
be a
![]() $\unicode[STIX]{x1D703}$
-stable Levi subgroup of
$\unicode[STIX]{x1D703}$
-stable Levi subgroup of
![]() $P^{n,\unicode[STIX]{x1D714}}$
. According to [Reference Brion and HelminckBH00], every maximal
$P^{n,\unicode[STIX]{x1D714}}$
. According to [Reference Brion and HelminckBH00], every maximal
![]() $\unicode[STIX]{x1D703}$
-stable parabolic subgroup of
$\unicode[STIX]{x1D703}$
-stable parabolic subgroup of
![]() $G$
is
$G$
is
![]() $K$
-conjugate to one of the above form.
$K$
-conjugate to one of the above form.
Let
![]() $\mathfrak{p}^{m}=\operatorname{Lie}\,P^{m}$
,
$\mathfrak{p}^{m}=\operatorname{Lie}\,P^{m}$
,
![]() $\mathfrak{p}_{1}^{m}=\mathfrak{p}^{m}\cap \mathfrak{g}_{1}$
, and
$\mathfrak{p}_{1}^{m}=\mathfrak{p}^{m}\cap \mathfrak{g}_{1}$
, and
![]() $(\mathfrak{n}_{P^{m}})_{1}=\mathfrak{n}_{P^{m}}\cap \mathfrak{g}_{1}$
, where
$(\mathfrak{n}_{P^{m}})_{1}=\mathfrak{n}_{P^{m}}\cap \mathfrak{g}_{1}$
, where
![]() $\mathfrak{n}_{P^{m}}$
is the nilpotent radical of
$\mathfrak{n}_{P^{m}}$
is the nilpotent radical of
![]() $\mathfrak{p}^{m}$
, etc.
$\mathfrak{p}^{m}$
, etc.
Proposition 3.1. We have the following.
(i) The map
is a small map onto its image, generically one-to-one. $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{m}^{N}:K\times ^{P_{K}^{m}}(\mathfrak{n}_{P^{m}})_{1}\rightarrow {\mathcal{N}}_{1},\quad (k,x)\mapsto \operatorname{Ad}k(x)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{m}^{N}:K\times ^{P_{K}^{m}}(\mathfrak{n}_{P^{m}})_{1}\rightarrow {\mathcal{N}}_{1},\quad (k,x)\mapsto \operatorname{Ad}k(x)\end{eqnarray}$$
(ii) The map
is a small map onto its image, generically one-to-one. $$\begin{eqnarray}\check{\unicode[STIX]{x1D70B}}_{m}^{N}:K\times ^{P_{K}^{m}}\mathfrak{p}_{1}^{m}\rightarrow \mathfrak{g}_{1},\quad (k,x)\mapsto \operatorname{Ad}k(x).\end{eqnarray}$$
$$\begin{eqnarray}\check{\unicode[STIX]{x1D70B}}_{m}^{N}:K\times ^{P_{K}^{m}}\mathfrak{p}_{1}^{m}\rightarrow \mathfrak{g}_{1},\quad (k,x)\mapsto \operatorname{Ad}k(x).\end{eqnarray}$$
The same holds for the two maps
![]() $\unicode[STIX]{x1D70B}_{n}^{2n,\unicode[STIX]{x1D714}}$
and
$\unicode[STIX]{x1D70B}_{n}^{2n,\unicode[STIX]{x1D714}}$
and
![]() $\check{\unicode[STIX]{x1D70B}}_{n}^{2n,\unicode[STIX]{x1D714}}$
defined using
$\check{\unicode[STIX]{x1D70B}}_{n}^{2n,\unicode[STIX]{x1D714}}$
defined using
![]() $P^{n,\unicode[STIX]{x1D714}}$
,
$P^{n,\unicode[STIX]{x1D714}}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
.
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
.
We define
For
![]() $m<N/2$
,
$m<N/2$
,
![]() $\mathfrak{g}_{1}^{m}$
consists of elements in
$\mathfrak{g}_{1}^{m}$
consists of elements in
![]() $\mathfrak{g}_{1}$
with eigenvalues
$\mathfrak{g}_{1}$
with eigenvalues
![]() $a_{1},a_{1},\ldots ,$
$a_{1},a_{1},\ldots ,$
![]() $a_{m},a_{m},$
$a_{m},a_{m},$
![]() $a_{j},j\in [2m+1,N]$
, where
$a_{j},j\in [2m+1,N]$
, where
![]() $\sum _{k=1}^{m}2a_{k}+\sum _{j=2m+1}^{N}a_{j}=0$
. Let
$\sum _{k=1}^{m}2a_{k}+\sum _{j=2m+1}^{N}a_{j}=0$
. Let
One checks readily that
![]() $\overline{Y_{m}^{r}}=\mathfrak{g}_{1}^{m}$
.
$\overline{Y_{m}^{r}}=\mathfrak{g}_{1}^{m}$
.
Consider the case
![]() $m=N/2=n$
. For
$m=N/2=n$
. For
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
, let
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
, let
where
![]() ${\mathcal{O}}_{2^{n}}^{\unicode[STIX]{x1D714}}$
is the nilpotent orbit given by the partition
${\mathcal{O}}_{2^{n}}^{\unicode[STIX]{x1D714}}$
is the nilpotent orbit given by the partition
![]() $2^{m}$
and defined by the equation
$2^{m}$
and defined by the equation
![]() $\operatorname{Im}\unicode[STIX]{x1D70B}_{n}^{2n,\unicode[STIX]{x1D714}}=\bar{{\mathcal{O}}}_{2^{n}}^{\unicode[STIX]{x1D714}}$
. Then
$\operatorname{Im}\unicode[STIX]{x1D70B}_{n}^{2n,\unicode[STIX]{x1D714}}=\bar{{\mathcal{O}}}_{2^{n}}^{\unicode[STIX]{x1D714}}$
. Then
![]() $Y_{n}^{r,\unicode[STIX]{x1D714}}$
is an open dense subset in
$Y_{n}^{r,\unicode[STIX]{x1D714}}$
is an open dense subset in
![]() $\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}}$
.
$\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}}$
.
Let
![]() $(\mathfrak{p}_{1}^{m})^{r}=\mathfrak{p}_{1}^{m}\cap Y_{m}^{r}$
and
$(\mathfrak{p}_{1}^{m})^{r}=\mathfrak{p}_{1}^{m}\cap Y_{m}^{r}$
and
![]() $(\mathfrak{l}_{1}^{m})^{\text{rs}}=\mathfrak{l}_{1}^{m}\cap (\mathfrak{l}^{m})^{\text{rs}}$
.
$(\mathfrak{l}_{1}^{m})^{\text{rs}}=\mathfrak{l}_{1}^{m}\cap (\mathfrak{l}^{m})^{\text{rs}}$
.
Proposition 3.2.
![]() $(1)$
Suppose that
$(1)$
Suppose that
![]() $1\leqslant m<N/2$
. There is a natural surjective map
$1\leqslant m<N/2$
. There is a natural surjective map
such that for an
![]() $L_{K}^{m}$
-equivariant local system
$L_{K}^{m}$
-equivariant local system
![]() ${\mathcal{T}}$
on
${\mathcal{T}}$
on
![]() $(\mathfrak{l}_{1}^{m})^{\text{rs}}$
associated to a
$(\mathfrak{l}_{1}^{m})^{\text{rs}}$
associated to a
![]() $\unicode[STIX]{x1D70B}_{1}^{L_{K}^{m}}((\mathfrak{l}_{1}^{m})^{\text{rs}})$
-representation
$\unicode[STIX]{x1D70B}_{1}^{L_{K}^{m}}((\mathfrak{l}_{1}^{m})^{\text{rs}})$
-representation
![]() $E$
, we have
$E$
, we have
where
![]() ${\mathcal{T}}^{\prime }$
is the
${\mathcal{T}}^{\prime }$
is the
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() $Y_{m}^{r}$
associated to the representation of
$Y_{m}^{r}$
associated to the representation of
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(Y_{m}^{r})$
which is obtained from
$\unicode[STIX]{x1D70B}_{1}^{K}(Y_{m}^{r})$
which is obtained from
![]() $E$
by pull-back under the map (3.2).
$E$
by pull-back under the map (3.2).
![]() $(2)$
We have a natural surjective map
$(2)$
We have a natural surjective map
such that for an
![]() $L_{K}^{n,\unicode[STIX]{x1D714}}$
-equivariant local system
$L_{K}^{n,\unicode[STIX]{x1D714}}$
-equivariant local system
![]() ${\mathcal{T}}$
on
${\mathcal{T}}$
on
![]() $(\mathfrak{l}_{1}^{n,\unicode[STIX]{x1D714}})^{\text{rs}}$
associated to a
$(\mathfrak{l}_{1}^{n,\unicode[STIX]{x1D714}})^{\text{rs}}$
associated to a
![]() $\unicode[STIX]{x1D70B}_{1}^{L_{K}^{n,\unicode[STIX]{x1D714}}}((L_{1}^{n,\unicode[STIX]{x1D714}})^{\text{rs}})$
-representation
$\unicode[STIX]{x1D70B}_{1}^{L_{K}^{n,\unicode[STIX]{x1D714}}}((L_{1}^{n,\unicode[STIX]{x1D714}})^{\text{rs}})$
-representation
![]() $E$
, we have
$E$
, we have
where
![]() ${\mathcal{T}}^{\prime }$
is the
${\mathcal{T}}^{\prime }$
is the
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() $Y_{n}^{r,\unicode[STIX]{x1D714}}$
associated to the representation of
$Y_{n}^{r,\unicode[STIX]{x1D714}}$
associated to the representation of
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(Y_{n}^{r,\unicode[STIX]{x1D714}})$
which is obtained from
$\unicode[STIX]{x1D70B}_{1}^{K}(Y_{n}^{r,\unicode[STIX]{x1D714}})$
which is obtained from
![]() $E$
by pull-back under the map (3.3).
$E$
by pull-back under the map (3.3).
3.1 Proof of Proposition 3.1
We begin with the proof of (1). Consider the following projection
When
![]() $m\neq N/2$
, the map
$m\neq N/2$
, the map
![]() $\unicode[STIX]{x1D70F}_{m}^{N}$
can be identified with the map
$\unicode[STIX]{x1D70F}_{m}^{N}$
can be identified with the map
![]() $\unicode[STIX]{x1D70B}_{m}^{N}$
. When
$\unicode[STIX]{x1D70B}_{m}^{N}$
. When
![]() $N=2m$
, the image of the map
$N=2m$
, the image of the map
![]() $\unicode[STIX]{x1D70F}_{m}^{2m}$
has two irreducible components, i.e., closures of the two orbits
$\unicode[STIX]{x1D70F}_{m}^{2m}$
has two irreducible components, i.e., closures of the two orbits
![]() ${\mathcal{O}}_{2^{m}}^{\text{I}}$
and
${\mathcal{O}}_{2^{m}}^{\text{I}}$
and
![]() ${\mathcal{O}}_{2^{m}}^{\text{II}}$
. The two maps
${\mathcal{O}}_{2^{m}}^{\text{II}}$
. The two maps
![]() $\unicode[STIX]{x1D70B}_{m}^{N,\text{I}}$
and
$\unicode[STIX]{x1D70B}_{m}^{N,\text{I}}$
and
![]() $\unicode[STIX]{x1D70B}_{m}^{N,\text{II}}$
can be identified with the map
$\unicode[STIX]{x1D70B}_{m}^{N,\text{II}}$
can be identified with the map
![]() $\unicode[STIX]{x1D70F}_{m}^{2m}$
restricted to
$\unicode[STIX]{x1D70F}_{m}^{2m}$
restricted to
![]() $\overline{(\unicode[STIX]{x1D70F}_{m}^{2m})^{-1}({\mathcal{O}}_{2^{m}}^{\text{I}})}$
and
$\overline{(\unicode[STIX]{x1D70F}_{m}^{2m})^{-1}({\mathcal{O}}_{2^{m}}^{\text{I}})}$
and
![]() $\overline{(\unicode[STIX]{x1D70F}_{m}^{2m})^{-1}({\mathcal{O}}_{2^{m}}^{\text{II}})}$
respectively. Thus it suffices to show that
$\overline{(\unicode[STIX]{x1D70F}_{m}^{2m})^{-1}({\mathcal{O}}_{2^{m}}^{\text{II}})}$
respectively. Thus it suffices to show that
When
![]() $m\neq N/2$
, one can check that the image of
$m\neq N/2$
, one can check that the image of
![]() $\unicode[STIX]{x1D70F}_{m}^{N}$
is as follows
$\unicode[STIX]{x1D70F}_{m}^{N}$
is as follows
Assume that
![]() $N\geqslant 3m$
and
$N\geqslant 3m$
and
![]() $x\in {\mathcal{O}}_{3^{m}1^{N-3m}}$
. Then
$x\in {\mathcal{O}}_{3^{m}1^{N-3m}}$
. Then
![]() $(\unicode[STIX]{x1D70F}_{m}^{N})^{-1}(x)$
consists of the flag
$(\unicode[STIX]{x1D70F}_{m}^{N})^{-1}(x)$
consists of the flag
![]() $0\subset V_{m}\subset V_{m}^{\bot }\subset V$
, where
$0\subset V_{m}\subset V_{m}^{\bot }\subset V$
, where
![]() $V_{m}=\operatorname{Im}x^{2}$
. Assume that
$V_{m}=\operatorname{Im}x^{2}$
. Assume that
![]() $N<3m$
and
$N<3m$
and
![]() $x\in {\mathcal{O}}_{3^{N-2m}2^{3m-N}}$
. Then
$x\in {\mathcal{O}}_{3^{N-2m}2^{3m-N}}$
. Then
![]() $(\unicode[STIX]{x1D70F}_{m}^{N})^{-1}(x)$
consists of the flag
$(\unicode[STIX]{x1D70F}_{m}^{N})^{-1}(x)$
consists of the flag
![]() $0\subset V_{m}\subset V_{m}^{\bot }\subset V$
, where
$0\subset V_{m}\subset V_{m}^{\bot }\subset V$
, where
![]() $V_{m}=\ker x$
. This proves that
$V_{m}=\ker x$
. This proves that
![]() $\unicode[STIX]{x1D70F}_{m}^{N}$
is generically one-to-one.
$\unicode[STIX]{x1D70F}_{m}^{N}$
is generically one-to-one.
Let
![]() $x\in {\mathcal{O}}_{3^{i}2^{j}1^{N-3i-2j}}\subset \operatorname{Im}\unicode[STIX]{x1D70F}_{m}^{N}$
. We assume that
$x\in {\mathcal{O}}_{3^{i}2^{j}1^{N-3i-2j}}\subset \operatorname{Im}\unicode[STIX]{x1D70F}_{m}^{N}$
. We assume that
![]() $3^{i}2^{j}1^{N-3i-2j}\neq 3^{m}1^{N-3m}$
if
$3^{i}2^{j}1^{N-3i-2j}\neq 3^{m}1^{N-3m}$
if
![]() $N\geqslant 3m$
, and
$N\geqslant 3m$
, and
![]() $3^{i}2^{j}1^{N-3i-2j}\neq 3^{N-2m}2^{3m-N}$
if
$3^{i}2^{j}1^{N-3i-2j}\neq 3^{N-2m}2^{3m-N}$
if
![]() $N<3m$
. It suffices to show that
$N<3m$
. It suffices to show that
Let
![]() $x_{0}\in {\mathcal{O}}_{2^{j}1^{N-3i-2j}}\subset \operatorname{Im}\unicode[STIX]{x1D70F}_{m-i}^{N-3i}$
. (Note that
$x_{0}\in {\mathcal{O}}_{2^{j}1^{N-3i-2j}}\subset \operatorname{Im}\unicode[STIX]{x1D70F}_{m-i}^{N-3i}$
. (Note that
![]() $\unicode[STIX]{x1D70F}_{m-i}^{N-3i}$
is defined since
$\unicode[STIX]{x1D70F}_{m-i}^{N-3i}$
is defined since
![]() $m-i\leqslant (N-3i)/2$
.) One checks readily that (using (2.2) for the second equality)
$m-i\leqslant (N-3i)/2$
.) One checks readily that (using (2.2) for the second equality)
Thus it suffices to show that
Let us write
and
To prove that the map
![]() $\unicode[STIX]{x1D70F}_{m}^{N}$
is small, we are reduced to proving that
$\unicode[STIX]{x1D70F}_{m}^{N}$
is small, we are reduced to proving that
To prove this we recall the partitioning of
![]() $\unicode[STIX]{x1D6FA}_{m,j}^{N}$
into
$\unicode[STIX]{x1D6FA}_{m,j}^{N}$
into
![]() $\unicode[STIX]{x1D6FA}_{m,j}^{N,k}$
given in [Reference Chen, Vilonen and XueCVX15b, § 2] as follows:
$\unicode[STIX]{x1D6FA}_{m,j}^{N,k}$
given in [Reference Chen, Vilonen and XueCVX15b, § 2] as follows:
We have
Recall that we have a surjective map
![]() $\unicode[STIX]{x1D6FA}_{m,j}^{N,k}\rightarrow \operatorname{OGr}(j-k,j)\times \operatorname{OGr}(m-k,N-2j)$
with fibers being affine spaces
$\unicode[STIX]{x1D6FA}_{m,j}^{N,k}\rightarrow \operatorname{OGr}(j-k,j)\times \operatorname{OGr}(m-k,N-2j)$
with fibers being affine spaces
![]() $\mathbb{A}^{(m-k)(j-k)}$
. We have
$\mathbb{A}^{(m-k)(j-k)}$
. We have
One checks that
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \text{if }j\geqslant N-2m,\quad \dim \overline{\unicode[STIX]{x1D6FA}_{m,j}^{N,k}}\text{ is maximal when }k=m+j-\bigg[{\displaystyle \frac{N}{2}}\bigg],\\ \text{if }j<N-2m,\quad \dim \overline{\unicode[STIX]{x1D6FA}_{m,j}^{N,k}}\text{ is maximal when }k=\bigg[{\displaystyle \frac{j+1}{2}}\bigg].\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \text{if }j\geqslant N-2m,\quad \dim \overline{\unicode[STIX]{x1D6FA}_{m,j}^{N,k}}\text{ is maximal when }k=m+j-\bigg[{\displaystyle \frac{N}{2}}\bigg],\\ \text{if }j<N-2m,\quad \dim \overline{\unicode[STIX]{x1D6FA}_{m,j}^{N,k}}\text{ is maximal when }k=\bigg[{\displaystyle \frac{j+1}{2}}\bigg].\end{array}\end{eqnarray}$$
Thus a direct calculation shows that
 $$\begin{eqnarray}\dim (\unicode[STIX]{x1D70B}_{m}^{N})^{-1}(\unicode[STIX]{x1D701}_{j})=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{a_{m,j}^{N}}{2}}+{\displaystyle \frac{j+m-N}{2}} & \text{if }j\geqslant N-2m\text{ and }N\text{ even},\text{ or }j<N-2m\text{ and }j\text{ odd},\\ {\displaystyle \frac{a_{m,j}^{N}}{2}}-{\displaystyle \frac{m}{2}} & \text{if }j\geqslant N-2m\text{ and }N\text{ odd},\text{ or }j<N-2m\text{ and }j\text{ even}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\dim (\unicode[STIX]{x1D70B}_{m}^{N})^{-1}(\unicode[STIX]{x1D701}_{j})=\left\{\begin{array}{@{}ll@{}}{\displaystyle \frac{a_{m,j}^{N}}{2}}+{\displaystyle \frac{j+m-N}{2}} & \text{if }j\geqslant N-2m\text{ and }N\text{ even},\text{ or }j<N-2m\text{ and }j\text{ odd},\\ {\displaystyle \frac{a_{m,j}^{N}}{2}}-{\displaystyle \frac{m}{2}} & \text{if }j\geqslant N-2m\text{ and }N\text{ odd},\text{ or }j<N-2m\text{ and }j\text{ even}.\end{array}\right.\end{eqnarray}$$
This proves (3.5) (note that
![]() $m+j<N$
). The proof of (3.4) is complete. This finishes the proof of the claim (1) in the proposition.
$m+j<N$
). The proof of (3.4) is complete. This finishes the proof of the claim (1) in the proposition.
It then follows that we have
where
Note that
![]() $K\times ^{P_{K}^{m}}\mathfrak{p}_{1}^{m}$
is the orthogonal complement of
$K\times ^{P_{K}^{m}}\mathfrak{p}_{1}^{m}$
is the orthogonal complement of
![]() $K\times ^{P_{K}^{m}}(\mathfrak{n}_{P^{m}})_{1}$
in the trivial bundle
$K\times ^{P_{K}^{m}}(\mathfrak{n}_{P^{m}})_{1}$
in the trivial bundle
![]() $K\times \mathfrak{g}_{1}$
over
$K\times \mathfrak{g}_{1}$
over
![]() $K/P_{K}^{m}$
. By the functoriality of Fourier transform, we have that
$K/P_{K}^{m}$
. By the functoriality of Fourier transform, we have that
Since Fourier transform sends simple perverse sheaves to simple perverse sheaves, we can conclude from (3.6) and (3.7) that
This proves the claim (2) of the proposition. The argument for
![]() $(\check{\unicode[STIX]{x1D70B}}_{n}^{2n})^{\unicode[STIX]{x1D714}}$
,
$(\check{\unicode[STIX]{x1D70B}}_{n}^{2n})^{\unicode[STIX]{x1D714}}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
, is the same. The proof of the proposition is complete.
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
, is the same. The proof of the proposition is complete.
3.2 Proof of Proposition 3.2
Note that we have that
To ease notation, let us now write that
![]() $L=L^{m}$
,
$L=L^{m}$
,
![]() $P=P^{m}$
, and
$P=P^{m}$
, and
![]() $\check{\unicode[STIX]{x1D70B}}=\check{\unicode[STIX]{x1D70B}}_{m}^{N}$
etc.
$\check{\unicode[STIX]{x1D70B}}=\check{\unicode[STIX]{x1D70B}}_{m}^{N}$
etc.
We first show the following.
Each element in
![]() $Y^{r}$
is
$Y^{r}$
is
![]() $K$
-conjugate to an element
$K$
-conjugate to an element
![]() $x_{0}\in \mathfrak{p}_{1}$
(see [Reference Kostant and RallisKR71, Theorem 7]), where
$x_{0}\in \mathfrak{p}_{1}$
(see [Reference Kostant and RallisKR71, Theorem 7]), where
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle x_{0}e_{i}=a_{i}e_{i},\quad x_{0}e_{N+1-i}=e_{i}+a_{i}e_{N+1-i}\quad \text{for }i\in [1,m],\\ x_{0}e_{j}=b_{j}e_{j}+c_{j}e_{N+1-j},\quad x_{0}e_{N+1-j}=c_{j}e_{j}+b_{j}e_{N+1-j}\quad \text{for }j\in [m+1,[N/2]]\\ \displaystyle x_{0}e_{(N+1)/2}=b_{(N+1)/2}e_{(N+1)/2}\quad \text{if }N\text{ is odd}\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle x_{0}e_{i}=a_{i}e_{i},\quad x_{0}e_{N+1-i}=e_{i}+a_{i}e_{N+1-i}\quad \text{for }i\in [1,m],\\ x_{0}e_{j}=b_{j}e_{j}+c_{j}e_{N+1-j},\quad x_{0}e_{N+1-j}=c_{j}e_{j}+b_{j}e_{N+1-j}\quad \text{for }j\in [m+1,[N/2]]\\ \displaystyle x_{0}e_{(N+1)/2}=b_{(N+1)/2}e_{(N+1)/2}\quad \text{if }N\text{ is odd}\end{array}\end{eqnarray}$$
and the numbers
![]() $a_{i},i=1,\ldots ,m,b_{j}+c_{j},b_{j}-c_{j},j=m+1,\ldots ,[N/2],b_{(N+1)/2}$
are distinct.
$a_{i},i=1,\ldots ,m,b_{j}+c_{j},b_{j}-c_{j},j=m+1,\ldots ,[N/2],b_{(N+1)/2}$
are distinct.
Thus it suffices to show that
![]() $\check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
consists of one point. Note that
$\check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
consists of one point. Note that
![]() $\check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
consists of
$\check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
consists of
![]() $x_{0}$
-stable
$x_{0}$
-stable
![]() $m$
-dimensional isotropic subspaces of
$m$
-dimensional isotropic subspaces of
![]() $V$
. Assume that
$V$
. Assume that
![]() $U_{m}\in \check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
. Then
$U_{m}\in \check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
. Then
![]() $U_{m}$
is a direct sum of generalized eigenspaces of
$U_{m}$
is a direct sum of generalized eigenspaces of
![]() $x_{0}$
. The generalized eigenspace of
$x_{0}$
. The generalized eigenspace of
![]() $x_{0}$
with eigenvalue
$x_{0}$
with eigenvalue
![]() $a_{i}$
is
$a_{i}$
is
![]() $\operatorname{span}\{e_{i},e_{N+1-i}\}$
,
$\operatorname{span}\{e_{i},e_{N+1-i}\}$
,
![]() $i=1,\ldots ,m$
, and the eigenspace of
$i=1,\ldots ,m$
, and the eigenspace of
![]() $x_{0}$
with eigenvalue
$x_{0}$
with eigenvalue
![]() $b_{j}\,+\,c_{j}$
,
$b_{j}\,+\,c_{j}$
,
![]() $b_{j}\,-\,c_{j}$
,
$b_{j}\,-\,c_{j}$
,
![]() $b_{(N+1)/2}$
is
$b_{(N+1)/2}$
is
![]() $\operatorname{span}\{e_{j}e_{N+1-j}\}$
,
$\operatorname{span}\{e_{j}e_{N+1-j}\}$
,
![]() $\operatorname{span}\{e_{j}+e_{N+1-j}\}$
,
$\operatorname{span}\{e_{j}+e_{N+1-j}\}$
,
![]() $\operatorname{span}\{e_{(N+1)/2}\}$
, respectively. Since
$\operatorname{span}\{e_{(N+1)/2}\}$
, respectively. Since
![]() $U_{m}$
is isotropic,
$U_{m}$
is isotropic,
![]() $U_{m}$
has to equal
$U_{m}$
has to equal
![]() $\operatorname{span}\{e_{i},i=1,\ldots ,m\}$
. This proves (3.9) for
$\operatorname{span}\{e_{i},i=1,\ldots ,m\}$
. This proves (3.9) for
![]() $\check{\unicode[STIX]{x1D70B}}_{m}$
,
$\check{\unicode[STIX]{x1D70B}}_{m}$
,
![]() $m<N/2$
. The proof for
$m<N/2$
. The proof for
![]() $\check{\unicode[STIX]{x1D70B}}_{n}^{\unicode[STIX]{x1D714}}$
is entirely similar and omitted.
$\check{\unicode[STIX]{x1D70B}}_{n}^{\unicode[STIX]{x1D714}}$
is entirely similar and omitted.
Now we show the following.
Let
![]() $x\in \mathfrak{p}_{1}^{r}$
. By the above proof of (3.9) we can assume that
$x\in \mathfrak{p}_{1}^{r}$
. By the above proof of (3.9) we can assume that
![]() $\operatorname{Ad}(k)x=x_{0}$
for some
$\operatorname{Ad}(k)x=x_{0}$
for some
![]() $k\in K$
, where
$k\in K$
, where
![]() $x_{0}$
is as in (3.10). Thus
$x_{0}$
is as in (3.10). Thus
![]() $(k,x)\in \check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
. It follows from (3.9) that
$(k,x)\in \check{\unicode[STIX]{x1D70B}}^{-1}(x_{0})$
. It follows from (3.9) that
![]() $(k,x)=(1,x_{0})\in K\times ^{P_{K}}\mathfrak{p}_{1}$
. Hence
$(k,x)=(1,x_{0})\in K\times ^{P_{K}}\mathfrak{p}_{1}$
. Hence
![]() $k\in P_{K}$
. Assume that
$k\in P_{K}$
. Assume that
![]() $k=lu$
where
$k=lu$
where
![]() $l\in L_{K}$
and
$l\in L_{K}$
and
![]() $u\in U_{K}=U\cap K$
(
$u\in U_{K}=U\cap K$
(
![]() $U$
is the unipotent radical of
$U$
is the unipotent radical of
![]() $P$
). Then we have
$P$
). Then we have
![]() $\operatorname{pr}(x)=\operatorname{pr}(\operatorname{Ad}(u^{-1}l^{-1})x_{0})=\operatorname{pr}(\operatorname{Ad}(l^{-1})x_{0})=\operatorname{Ad}(l^{-1})\operatorname{pr}(x_{0})$
. It is clear that
$\operatorname{pr}(x)=\operatorname{pr}(\operatorname{Ad}(u^{-1}l^{-1})x_{0})=\operatorname{pr}(\operatorname{Ad}(l^{-1})x_{0})=\operatorname{Ad}(l^{-1})\operatorname{pr}(x_{0})$
. It is clear that
![]() $\operatorname{pr}(x_{0})\in \mathfrak{l}^{\text{rs}}$
. Thus (3.11) follows.
$\operatorname{pr}(x_{0})\in \mathfrak{l}^{\text{rs}}$
. Thus (3.11) follows.
By (3.9) and (3.11), we have the following diagram, when restricting (2.10) to
![]() $Y^{r}$
,
$Y^{r}$
,
Using (3.9), we see that
Finally, the canonical map
![]() $\unicode[STIX]{x1D70B}_{1}^{P_{K}}(\mathfrak{p}_{1}^{r})\rightarrow \unicode[STIX]{x1D70B}_{1}^{P_{K}}(\mathfrak{l}_{1}^{\text{rs}})\cong \unicode[STIX]{x1D70B}_{1}^{L_{K}}(\mathfrak{l}_{1}^{\text{rs}})$
is surjective. We see this as follows. First, the canonical map above can be identified with the canonical map
$\unicode[STIX]{x1D70B}_{1}^{P_{K}}(\mathfrak{p}_{1}^{r})\rightarrow \unicode[STIX]{x1D70B}_{1}^{P_{K}}(\mathfrak{l}_{1}^{\text{rs}})\cong \unicode[STIX]{x1D70B}_{1}^{L_{K}}(\mathfrak{l}_{1}^{\text{rs}})$
is surjective. We see this as follows. First, the canonical map above can be identified with the canonical map
![]() $\unicode[STIX]{x1D70B}_{1}^{P_{K}}(\mathfrak{p}_{1}^{r})\rightarrow \unicode[STIX]{x1D70B}_{1}^{P_{K}}(\operatorname{pr}^{-1}(\mathfrak{l}_{1}^{\text{rs}}))$
. Now, because
$\unicode[STIX]{x1D70B}_{1}^{P_{K}}(\mathfrak{p}_{1}^{r})\rightarrow \unicode[STIX]{x1D70B}_{1}^{P_{K}}(\operatorname{pr}^{-1}(\mathfrak{l}_{1}^{\text{rs}}))$
. Now, because
![]() $\mathfrak{p}_{1}^{r}$
is an open subset in
$\mathfrak{p}_{1}^{r}$
is an open subset in
![]() $\operatorname{pr}^{-1}(\mathfrak{l}_{1}^{\text{rs}})$
, which is smooth, the map
$\operatorname{pr}^{-1}(\mathfrak{l}_{1}^{\text{rs}})$
, which is smooth, the map
![]() $\unicode[STIX]{x1D70B}_{1}(\mathfrak{p}_{1}^{r})\rightarrow \unicode[STIX]{x1D70B}_{1}(\operatorname{pr}^{-1}(\mathfrak{l}_{1}^{\text{rs}}))$
is a surjection. To conclude that this property persists when we pass to the equivariant fundamental group it suffices to remark that the equivariant fundamental group is always a quotient of the ordinary fundamental group as long as the group is connected. We now conclude the argument making use of Proposition 3.1.
$\unicode[STIX]{x1D70B}_{1}(\mathfrak{p}_{1}^{r})\rightarrow \unicode[STIX]{x1D70B}_{1}(\operatorname{pr}^{-1}(\mathfrak{l}_{1}^{\text{rs}}))$
is a surjection. To conclude that this property persists when we pass to the equivariant fundamental group it suffices to remark that the equivariant fundamental group is always a quotient of the ordinary fundamental group as long as the group is connected. We now conclude the argument making use of Proposition 3.1.
4 Fourier transform of nilpotent orbital complexes for
 $(\text{SL}(N),\text{SO}(N))$
$(\text{SL}(N),\text{SO}(N))$
Consider the symmetric pair
![]() $(G,K)=(\text{SL}(N),\text{SO}(N))$
. Let us write
$(G,K)=(\text{SL}(N),\text{SO}(N))$
. Let us write
![]() ${\mathcal{A}}_{N}$
for the set of all simple
${\mathcal{A}}_{N}$
for the set of all simple
![]() $K$
-equivariant perverse sheaves on
$K$
-equivariant perverse sheaves on
![]() ${\mathcal{N}}_{1}$
(up to isomorphism), that is, the set of IC complexes
${\mathcal{N}}_{1}$
(up to isomorphism), that is, the set of IC complexes
![]() $\operatorname{IC}({\mathcal{O}},{\mathcal{E}})$
, where
$\operatorname{IC}({\mathcal{O}},{\mathcal{E}})$
, where
![]() ${\mathcal{O}}$
is a
${\mathcal{O}}$
is a
![]() $K$
-orbit in
$K$
-orbit in
![]() ${\mathcal{N}}_{1}$
and
${\mathcal{N}}_{1}$
and
![]() ${\mathcal{E}}$
is an irreducible
${\mathcal{E}}$
is an irreducible
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() ${\mathcal{O}}$
(up to isomorphism). An IC complex in
${\mathcal{O}}$
(up to isomorphism). An IC complex in
![]() ${\mathcal{A}}_{N}$
is called a nilpotent orbital complex.
${\mathcal{A}}_{N}$
is called a nilpotent orbital complex.
Let
![]() $n=[N/2]$
. We set
$n=[N/2]$
. We set
In the case when
![]() $N$
is even, we identify the triple
$N$
is even, we identify the triple
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
with
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
with
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{2},\unicode[STIX]{x1D707}^{1})$
if
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{2},\unicode[STIX]{x1D707}^{1})$
if
![]() $|\unicode[STIX]{x1D707}^{1}|=|\unicode[STIX]{x1D707}^{2}|$
and
$|\unicode[STIX]{x1D707}^{1}|=|\unicode[STIX]{x1D707}^{2}|$
and
![]() $\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2}$
, and the triples
$\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2}$
, and the triples
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})$
attain two labels
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})$
attain two labels
![]() $\text{I}$
and
$\text{I}$
and
![]() $\text{II}$
.
$\text{II}$
.
Given a triple
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
(respectively
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
(respectively
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
), where
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
), where
![]() $|\unicode[STIX]{x1D708}|=m<N/2$
, we define an irreducible
$|\unicode[STIX]{x1D708}|=m<N/2$
, we define an irreducible
![]() $K$
-equivariant local system
$K$
-equivariant local system
![]() ${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
(respectively
${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
(respectively
![]() ${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}$
) on
${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}$
) on
![]() $Y_{m}^{r}$
(here we write
$Y_{m}^{r}$
(here we write
![]() $Y_{0}^{r}=\mathfrak{g}_{1}^{\text{rs}}$
) as follows. We obtain a map
$Y_{0}^{r}=\mathfrak{g}_{1}^{\text{rs}}$
) as follows. We obtain a map
by composing the map in (3.2) with the natural map
![]() $B_{m}\times \widetilde{B}_{N-2m}\rightarrow S_{m}\times \widetilde{B}_{N-2m}$
. Note that the map
$B_{m}\times \widetilde{B}_{N-2m}\rightarrow S_{m}\times \widetilde{B}_{N-2m}$
. Note that the map
![]() $\unicode[STIX]{x1D70F}$
is surjective. Then
$\unicode[STIX]{x1D70F}$
is surjective. Then
![]() ${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
(respectively
${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
(respectively
![]() ${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}$
) is the irreducible local system associated to the irreducible representation of
${\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}$
) is the irreducible local system associated to the irreducible representation of
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(Y_{m}^{r})$
given by pulling back the irreducible representation
$\unicode[STIX]{x1D70B}_{1}^{K}(Y_{m}^{r})$
given by pulling back the irreducible representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
(respectively
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
(respectively
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D714}}$
) via the map
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D714}}$
) via the map
![]() $\unicode[STIX]{x1D70F}$
; here
$\unicode[STIX]{x1D70F}$
; here
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\in S_{m}^{\vee }$
is the irreducible representation of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\in S_{m}^{\vee }$
is the irreducible representation of
![]() $S_{m}$
corresponding to
$S_{m}$
corresponding to
![]() $\unicode[STIX]{x1D708}\in {\mathcal{P}}(m)$
and
$\unicode[STIX]{x1D708}\in {\mathcal{P}}(m)$
and
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
(respectively
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
(respectively
![]() $V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D714}}$
) is the irreducible representation of
$V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D714}}$
) is the irreducible representation of
![]() $\widetilde{B}_{N-2m}$
defined in (2.7) (respectively (2.9)).
$\widetilde{B}_{N-2m}$
defined in (2.7) (respectively (2.9)).
Assume now that
![]() $N=2n$
. Given a triple
$N=2n$
. Given a triple
![]() $(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
$(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
, we define the irreducible
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
, we define the irreducible
![]() $K$
-equivariant local system
$K$
-equivariant local system
![]() ${\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}}$
on
${\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}}$
on
![]() $(Y_{n}^{r})^{\unicode[STIX]{x1D714}}$
as the local system associated to the representation of
$(Y_{n}^{r})^{\unicode[STIX]{x1D714}}$
as the local system associated to the representation of
![]() $\unicode[STIX]{x1D70B}_{1}^{K}((Y_{n}^{r})^{\unicode[STIX]{x1D714}})$
obtained by pulling back the representation
$\unicode[STIX]{x1D70B}_{1}^{K}((Y_{n}^{r})^{\unicode[STIX]{x1D714}})$
obtained by pulling back the representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\in S_{n}^{\vee }$
corresponding to
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\in S_{n}^{\vee }$
corresponding to
![]() $\unicode[STIX]{x1D708}\in {\mathcal{P}}(n)$
under that map
$\unicode[STIX]{x1D708}\in {\mathcal{P}}(n)$
under that map
Now we are ready to formulate our main result.
Theorem 4.1. The Fourier transform
![]() $\mathfrak{F}:\operatorname{Perv}_{K}(\mathfrak{g}_{1})\rightarrow \operatorname{Perv}_{K}(\mathfrak{g}_{1})$
induces a bijection
$\mathfrak{F}:\operatorname{Perv}_{K}(\mathfrak{g}_{1})\rightarrow \operatorname{Perv}_{K}(\mathfrak{g}_{1})$
induces a bijection
 $$\begin{eqnarray}\begin{array}{@{}rl@{}}\displaystyle \mathfrak{F}:{\mathcal{A}}_{N}\xrightarrow[{}]{{\sim}}\, & \big\{\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}))\mid (\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N},\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2},~|\unicode[STIX]{x1D708}|=m<N/2\big\}\\ \, & \cup \,\big\{\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})\mid (\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N},\unicode[STIX]{x1D714}=\text{I},\text{II},~|\unicode[STIX]{x1D708}|=m<N/2\big\}\quad (\text{if }N\text{ is even}),\\ \, & \cup \,\big\{\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}})\mid (\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N},\unicode[STIX]{x1D714}=\text{I},\text{II},~|\unicode[STIX]{x1D708}|=n=N/2\big\}\quad (\text{if }N\text{ is even}),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rl@{}}\displaystyle \mathfrak{F}:{\mathcal{A}}_{N}\xrightarrow[{}]{{\sim}}\, & \big\{\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}))\mid (\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N},\unicode[STIX]{x1D707}^{1}\neq \unicode[STIX]{x1D707}^{2},~|\unicode[STIX]{x1D708}|=m<N/2\big\}\\ \, & \cup \,\big\{\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})\mid (\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N},\unicode[STIX]{x1D714}=\text{I},\text{II},~|\unicode[STIX]{x1D708}|=m<N/2\big\}\quad (\text{if }N\text{ is even}),\\ \, & \cup \,\big\{\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}})\mid (\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N},\unicode[STIX]{x1D714}=\text{I},\text{II},~|\unicode[STIX]{x1D708}|=n=N/2\big\}\quad (\text{if }N\text{ is even}),\end{array}\end{eqnarray}$$
where
![]() $\mathfrak{g}_{1}^{0}=\mathfrak{g}_{1}$
,
$\mathfrak{g}_{1}^{0}=\mathfrak{g}_{1}$
,
![]() $\mathfrak{g}_{1}^{m}$
and
$\mathfrak{g}_{1}^{m}$
and
![]() $\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}}$
are defined in (3.1).
$\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}}$
are defined in (3.1).
4.1 Proof of Theorem 4.1
Let
![]() $p(k)$
denote the number of partitions of
$p(k)$
denote the number of partitions of
![]() $k$
and let
$k$
and let
![]() $q(k)$
denote the number of 2-regular partitions of
$q(k)$
denote the number of 2-regular partitions of
![]() $k$
. We write
$k$
. We write
![]() $p(0)=q(0)=1$
. Let us define
$p(0)=q(0)=1$
. Let us define
Lemma 4.2. We have
Proof. Note that
Let
![]() $p(l,k)$
denote the number of partitions of
$p(l,k)$
denote the number of partitions of
![]() $l$
into (not necessarily distinct) parts of exactly
$l$
into (not necessarily distinct) parts of exactly
![]() $k$
different sizes. We have (see for example [Reference WilfWil83])
$k$
different sizes. We have (see for example [Reference WilfWil83])
Assume first that
![]() $N=2n+1$
. Note that if
$N=2n+1$
. Note that if
![]() $\unicode[STIX]{x1D706}$
is a partition of
$\unicode[STIX]{x1D706}$
is a partition of
![]() $N$
with parts of
$N$
with parts of
![]() $k$
different sizes, then the component group
$k$
different sizes, then the component group
![]() $A_{K}(x)$
of the centralizer
$A_{K}(x)$
of the centralizer
![]() $Z_{K}(x)$
for
$Z_{K}(x)$
for
![]() $x\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}$
is
$x\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}$
is
![]() $(\mathbb{Z}/2\mathbb{Z})^{k-1}$
. Thus there are
$(\mathbb{Z}/2\mathbb{Z})^{k-1}$
. Thus there are
![]() $2^{k-1}$
irreducible
$2^{k-1}$
irreducible
![]() $K$
-equivariant local systems on
$K$
-equivariant local systems on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(up to isomorphism). Hence using (4.6), we see that
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(up to isomorphism). Hence using (4.6), we see that
Using (4.5), we see that
It then follows that
![]() $|{\mathcal{A}}_{2n+1}|$
is the desired number. The fact that
$|{\mathcal{A}}_{2n+1}|$
is the desired number. The fact that
![]() $|\unicode[STIX]{x1D6F4}_{2n+1}|$
equals the same number is clear from the definition. Thus (4.3) holds.
$|\unicode[STIX]{x1D6F4}_{2n+1}|$
equals the same number is clear from the definition. Thus (4.3) holds.
Assume now that
![]() $N=2n$
. Suppose that
$N=2n$
. Suppose that
![]() $\unicode[STIX]{x1D706}$
is a partition of
$\unicode[STIX]{x1D706}$
is a partition of
![]() $N$
with parts of exactly
$N$
with parts of exactly
![]() $k$
different sizes. If
$k$
different sizes. If
![]() $\unicode[STIX]{x1D706}$
has at least one odd part, then there are
$\unicode[STIX]{x1D706}$
has at least one odd part, then there are
![]() $2^{k-1}$
irreducible
$2^{k-1}$
irreducible
![]() $K$
-equivariant local systems on
$K$
-equivariant local systems on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(up to isomorphism). If
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(up to isomorphism). If
![]() $\unicode[STIX]{x1D706}$
has only even parts, then there are
$\unicode[STIX]{x1D706}$
has only even parts, then there are
![]() $2^{k}$
irreducible
$2^{k}$
irreducible
![]() $K$
-equivariant local systems on each
$K$
-equivariant local systems on each
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
(up to isomorphism),
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
(up to isomorphism),
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
.
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
.
Thus we have that
 $$\begin{eqnarray}\displaystyle |{\mathcal{A}}_{2n}| & = & \displaystyle \mathop{\sum }_{k\geqslant 0}p(2n,k)\,2^{k-1}+\mathop{\sum }_{k\geqslant 0}p(n,k)\,3\cdot 2^{k-1}\nonumber\\ \displaystyle \displaystyle & = & \displaystyle \text{Coefficient of }x^{2n}\text{ in }{\displaystyle \frac{1}{2}}\mathop{\prod }_{s\geqslant 1}\bigg({\displaystyle \frac{1+x^{s}}{1-x^{s}}}\bigg)+\text{Coefficient of }x^{n}\text{ in }{\displaystyle \frac{3}{2}}\mathop{\prod }_{s\geqslant 1}\bigg({\displaystyle \frac{1+x^{s}}{1-x^{s}}}\bigg)\nonumber\\ \displaystyle \displaystyle & = & \displaystyle {\displaystyle \frac{1}{2}}\bigg(\mathop{\sum }_{k=0}^{n}p(n-k)\bigg(2\mathop{\sum }_{s=0}^{k-1}q(s)q(2k-s)+q(k)^{2}\bigg)\!\bigg)+{\displaystyle \frac{3}{2}}\mathop{\sum }_{k=0}^{n}p(n-k)q(k)=\mathop{\sum }_{k=0}^{n}p(n-k)e(k).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle |{\mathcal{A}}_{2n}| & = & \displaystyle \mathop{\sum }_{k\geqslant 0}p(2n,k)\,2^{k-1}+\mathop{\sum }_{k\geqslant 0}p(n,k)\,3\cdot 2^{k-1}\nonumber\\ \displaystyle \displaystyle & = & \displaystyle \text{Coefficient of }x^{2n}\text{ in }{\displaystyle \frac{1}{2}}\mathop{\prod }_{s\geqslant 1}\bigg({\displaystyle \frac{1+x^{s}}{1-x^{s}}}\bigg)+\text{Coefficient of }x^{n}\text{ in }{\displaystyle \frac{3}{2}}\mathop{\prod }_{s\geqslant 1}\bigg({\displaystyle \frac{1+x^{s}}{1-x^{s}}}\bigg)\nonumber\\ \displaystyle \displaystyle & = & \displaystyle {\displaystyle \frac{1}{2}}\bigg(\mathop{\sum }_{k=0}^{n}p(n-k)\bigg(2\mathop{\sum }_{s=0}^{k-1}q(s)q(2k-s)+q(k)^{2}\bigg)\!\bigg)+{\displaystyle \frac{3}{2}}\mathop{\sum }_{k=0}^{n}p(n-k)q(k)=\mathop{\sum }_{k=0}^{n}p(n-k)e(k).\nonumber\end{eqnarray}$$
Here we have used (4.7) and the following equation
Again the fact that
![]() $|\unicode[STIX]{x1D6F4}_{2n}|$
equals the desired number is clear from the definition.◻
$|\unicode[STIX]{x1D6F4}_{2n}|$
equals the desired number is clear from the definition.◻
Note that the IC sheaves appearing on the right-hand side of the Fourier transform map
![]() $\mathfrak{F}$
in Theorem 4.1 are pairwise non-isomorphic. Thus, in view of Lemma 4.2, Theorem 4.1 follows from the following.
$\mathfrak{F}$
in Theorem 4.1 are pairwise non-isomorphic. Thus, in view of Lemma 4.2, Theorem 4.1 follows from the following.
Proposition 4.3. Let
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
(respectively
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
(respectively
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
) and write
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
) and write
![]() $m=|\unicode[STIX]{x1D708}|$
. The Fourier transform of
$m=|\unicode[STIX]{x1D708}|$
. The Fourier transform of
![]() $\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}))$
(respectively
$\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}))$
(respectively
![]() $\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})$
,
$\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})$
,
![]() $\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}})$
) is supported on a
$\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}})$
) is supported on a
![]() $K$
-orbit in
$K$
-orbit in
![]() ${\mathcal{N}}_{1}$
.
${\mathcal{N}}_{1}$
.
Proof. Let
![]() $n=[N/2]$
. We begin the proof by showing the following for
$n=[N/2]$
. We begin the proof by showing the following for
![]() $(\emptyset ;\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
(respectively
$(\emptyset ;\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
(respectively
![]() $(\emptyset ;\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
$(\emptyset ;\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{N}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
).
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
).
Recall that
![]() ${\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
(respectively
${\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})$
(respectively
![]() ${\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}$
) is the irreducible
${\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}$
) is the irreducible
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() $\mathfrak{g}_{1}^{\text{rs}}$
corresponding to
$\mathfrak{g}_{1}^{\text{rs}}$
corresponding to
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
(respectively
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
(respectively
![]() $V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D714}}$
).
$V_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D707}}^{\unicode[STIX]{x1D714}}$
).
We will now appeal to the nearby cycle construction in [Reference Grinberg, Vilonen and XueGVX18]. Let us recall the characters
![]() $\unicode[STIX]{x1D712}_{m}\in I_{N}^{\vee }$
,
$\unicode[STIX]{x1D712}_{m}\in I_{N}^{\vee }$
,
![]() $0\leqslant m\leqslant n$
of (2.3). In [Reference Grinberg, Vilonen and XueGVX18] we apply a nearby cycle construction to local systems associated to the
$0\leqslant m\leqslant n$
of (2.3). In [Reference Grinberg, Vilonen and XueGVX18] we apply a nearby cycle construction to local systems associated to the
![]() $\unicode[STIX]{x1D712}_{m}$
and obtain a
$\unicode[STIX]{x1D712}_{m}$
and obtain a
![]() $K$
-equivariant perverse sheaf
$K$
-equivariant perverse sheaf
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D712}_{m}}$
on the nilpotent cone
${\mathcal{P}}_{\unicode[STIX]{x1D712}_{m}}$
on the nilpotent cone
![]() ${\mathcal{N}}_{1}$
. More precisely, for each character
${\mathcal{N}}_{1}$
. More precisely, for each character
![]() $\unicode[STIX]{x1D712}_{m}$
, let us write
$\unicode[STIX]{x1D712}_{m}$
, let us write
![]() $W_{\unicode[STIX]{x1D712}_{m}}=\operatorname{Stab}_{W}(\unicode[STIX]{x1D712}_{m})$
. Consider the following base-change diagram of the adjoint quotient map.
$W_{\unicode[STIX]{x1D712}_{m}}=\operatorname{Stab}_{W}(\unicode[STIX]{x1D712}_{m})$
. Consider the following base-change diagram of the adjoint quotient map.

Let us write
![]() $\mathfrak{g}_{1,\unicode[STIX]{x1D712}_{m}}^{\text{rs}}$
for the base change of the regular semisimple locus
$\mathfrak{g}_{1,\unicode[STIX]{x1D712}_{m}}^{\text{rs}}$
for the base change of the regular semisimple locus
![]() $\mathfrak{g}_{1}^{\text{rs}}$
. Denote by
$\mathfrak{g}_{1}^{\text{rs}}$
. Denote by
![]() ${\mathcal{F}}_{\unicode[STIX]{x1D712}_{m}}$
the
${\mathcal{F}}_{\unicode[STIX]{x1D712}_{m}}$
the
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() $\mathfrak{g}_{1,\unicode[STIX]{x1D712}_{m}}^{\text{rs}}$
corresponding to the representation of
$\mathfrak{g}_{1,\unicode[STIX]{x1D712}_{m}}^{\text{rs}}$
corresponding to the representation of
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1,\unicode[STIX]{x1D712}_{m}}^{\text{rs}})=I_{N}\rtimes B_{\unicode[STIX]{x1D712}_{m}}$
, where
$\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1,\unicode[STIX]{x1D712}_{m}}^{\text{rs}})=I_{N}\rtimes B_{\unicode[STIX]{x1D712}_{m}}$
, where
![]() $I_{N}$
acts via the character
$I_{N}$
acts via the character
![]() $\unicode[STIX]{x1D712}_{m}$
and
$\unicode[STIX]{x1D712}_{m}$
and
![]() $B_{\unicode[STIX]{x1D712}_{m}}$
acts trivially (recall that
$B_{\unicode[STIX]{x1D712}_{m}}$
acts trivially (recall that
![]() $B_{\unicode[STIX]{x1D712}_{m}}=\operatorname{Stab}_{B_{N}}(\unicode[STIX]{x1D712}_{m})$
). We form the nearby cycle sheaf
$B_{\unicode[STIX]{x1D712}_{m}}=\operatorname{Stab}_{B_{N}}(\unicode[STIX]{x1D712}_{m})$
). We form the nearby cycle sheaf
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D712}_{m}}=\unicode[STIX]{x1D713}_{f_{\unicode[STIX]{x1D712}_{m}}}{\mathcal{F}}_{\unicode[STIX]{x1D712}_{m}}$
, appropriately shifted, so that
${\mathcal{P}}_{\unicode[STIX]{x1D712}_{m}}=\unicode[STIX]{x1D713}_{f_{\unicode[STIX]{x1D712}_{m}}}{\mathcal{F}}_{\unicode[STIX]{x1D712}_{m}}$
, appropriately shifted, so that
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D712}_{m}}\in \operatorname{Perv}_{K}({\mathcal{N}}_{1})$
.
${\mathcal{P}}_{\unicode[STIX]{x1D712}_{m}}\in \operatorname{Perv}_{K}({\mathcal{N}}_{1})$
.
Applying [Reference Grinberg, Vilonen and XueGVX18, Theorem 3.2], we obtain that
where
![]() ${\mathcal{M}}_{\unicode[STIX]{x1D712}_{m}}$
is the
${\mathcal{M}}_{\unicode[STIX]{x1D712}_{m}}$
is the
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() $\mathfrak{g}_{1}^{\text{rs}}$
corresponding to the
$\mathfrak{g}_{1}^{\text{rs}}$
corresponding to the
![]() $\widetilde{B}_{N}$
-representation
$\widetilde{B}_{N}$
-representation
Let us explain the notation in the above formula in our setting. Let
![]() $W_{\unicode[STIX]{x1D712}_{m}}^{0}$
be the Coxeter subgroup of
$W_{\unicode[STIX]{x1D712}_{m}}^{0}$
be the Coxeter subgroup of
![]() $W$
generated by
$W$
generated by
![]() $s_{\unicode[STIX]{x1D6FC}}$
with
$s_{\unicode[STIX]{x1D6FC}}$
with
![]() $\unicode[STIX]{x1D712}_{m}(\check{\unicode[STIX]{x1D6FC}}(-1))=1$
,
$\unicode[STIX]{x1D712}_{m}(\check{\unicode[STIX]{x1D6FC}}(-1))=1$
,
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}(\mathfrak{g},\mathfrak{a})$
, where
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6F7}(\mathfrak{g},\mathfrak{a})$
, where
![]() $\unicode[STIX]{x1D6F7}(\mathfrak{g},\mathfrak{a})$
is the root system of
$\unicode[STIX]{x1D6F7}(\mathfrak{g},\mathfrak{a})$
is the root system of
![]() $\mathfrak{g}$
with respect to
$\mathfrak{g}$
with respect to
![]() $\mathfrak{a}$
. Note that
$\mathfrak{a}$
. Note that
![]() $\check{\unicode[STIX]{x1D6FC}}(-1)\in I_{N}$
. Then
$\check{\unicode[STIX]{x1D6FC}}(-1)\in I_{N}$
. Then
![]() ${\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}}$
is the Hecke algebra associated to the Coxeter group
${\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}}$
is the Hecke algebra associated to the Coxeter group
![]() $W_{\unicode[STIX]{x1D712}_{m}}^{0}$
with parameter
$W_{\unicode[STIX]{x1D712}_{m}}^{0}$
with parameter
![]() $-1$
. Let
$-1$
. Let
![]() $B_{\unicode[STIX]{x1D712}_{m}}^{0}\subset B_{N}$
be the inverse image of
$B_{\unicode[STIX]{x1D712}_{m}}^{0}\subset B_{N}$
be the inverse image of
![]() $W_{\unicode[STIX]{x1D712}_{m}}^{0}\subset W$
under the natural map
$W_{\unicode[STIX]{x1D712}_{m}}^{0}\subset W$
under the natural map
![]() $B_{N}\rightarrow W=S_{N}$
. Then
$B_{N}\rightarrow W=S_{N}$
. Then
![]() $\widetilde{B}_{\unicode[STIX]{x1D712}_{m}}^{0}=I_{N}\rtimes B_{\unicode[STIX]{x1D712}_{m}}^{0}$
. In our setting, one readily checks that
$\widetilde{B}_{\unicode[STIX]{x1D712}_{m}}^{0}=I_{N}\rtimes B_{\unicode[STIX]{x1D712}_{m}}^{0}$
. In our setting, one readily checks that
![]() $W_{\unicode[STIX]{x1D712}_{m}}^{0}=\langle s_{i},i\neq m\rangle$
,
$W_{\unicode[STIX]{x1D712}_{m}}^{0}=\langle s_{i},i\neq m\rangle$
,
![]() ${\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}}={\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
and
${\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}}={\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
and
![]() $B_{\unicode[STIX]{x1D712}_{m}}^{0}=B_{m,N-m}$
(here we use the notation in §2.3). The action of
$B_{\unicode[STIX]{x1D712}_{m}}^{0}=B_{m,N-m}$
(here we use the notation in §2.3). The action of
![]() $\widetilde{B}_{\unicode[STIX]{x1D712}_{m}}^{0}$
on
$\widetilde{B}_{\unicode[STIX]{x1D712}_{m}}^{0}$
on
![]() $(\mathbb{C}_{\unicode[STIX]{x1D712}_{m}}\otimes {\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}})$
is given by
$(\mathbb{C}_{\unicode[STIX]{x1D712}_{m}}\otimes {\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}})$
is given by
![]() $I_{N}$
acting via the character
$I_{N}$
acting via the character
![]() $\unicode[STIX]{x1D712}_{m}$
and
$\unicode[STIX]{x1D712}_{m}$
and
![]() $B_{\unicode[STIX]{x1D712}_{m}}^{0}$
acting via the quotient map
$B_{\unicode[STIX]{x1D712}_{m}}^{0}$
acting via the quotient map
![]() $\mathbb{C}[B_{\unicode[STIX]{x1D712}_{m}}^{0}]\rightarrow {\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}}$
. Thus we conclude
$\mathbb{C}[B_{\unicode[STIX]{x1D712}_{m}}^{0}]\rightarrow {\mathcal{H}}_{W_{\unicode[STIX]{x1D712}_{m}}^{0}}$
. Thus we conclude
where
![]() ${\mathcal{L}}_{\unicode[STIX]{x1D712}_{m}}$
is the
${\mathcal{L}}_{\unicode[STIX]{x1D712}_{m}}$
is the
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() $\mathfrak{g}_{1}^{\text{rs}}$
corresponding to the representations
$\mathfrak{g}_{1}^{\text{rs}}$
corresponding to the representations
![]() $L_{\unicode[STIX]{x1D712}_{m}}$
of
$L_{\unicode[STIX]{x1D712}_{m}}$
of
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}})=\widetilde{B}_{N}$
defined in (2.8).
$\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}})=\widetilde{B}_{N}$
defined in (2.8).
By Lemma 2.1 the IC sheaves
![]() $\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}))$
and
$\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}))$
and
![]() $\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})$
are composition factors of the
$\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{T}}(\emptyset ;\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})$
are composition factors of the
![]() $\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{L}}_{\unicode[STIX]{x1D712}_{m}})$
. Hence (4.8) follows from (4.10).
$\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{L}}_{\unicode[STIX]{x1D712}_{m}})$
. Hence (4.8) follows from (4.10).
Now let
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
with
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
with
![]() $|\unicode[STIX]{x1D708}|=m>0$
. Let
$|\unicode[STIX]{x1D708}|=m>0$
. Let
denote the irreducible
![]() $L_{K}$
-equivariant local system on
$L_{K}$
-equivariant local system on
![]() $\mathfrak{l}_{1}^{\text{rs}}$
associated to the irreducible representation of
$\mathfrak{l}_{1}^{\text{rs}}$
associated to the irreducible representation of
![]() $\unicode[STIX]{x1D70B}_{1}^{L_{K}}(\mathfrak{l}_{1}^{\text{rs}})$
obtained as a pullback of
$\unicode[STIX]{x1D70B}_{1}^{L_{K}}(\mathfrak{l}_{1}^{\text{rs}})$
obtained as a pullback of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
via the map
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
via the map
![]() $\unicode[STIX]{x1D70B}_{1}^{L_{K}}(\mathfrak{l}_{1}^{\text{rs}})\cong B_{m}\times \widetilde{B}_{N-2m}{\twoheadrightarrow}S_{m}\times \widetilde{B}_{N-2m}$
.
$\unicode[STIX]{x1D70B}_{1}^{L_{K}}(\mathfrak{l}_{1}^{\text{rs}})\cong B_{m}\times \widetilde{B}_{N-2m}{\twoheadrightarrow}S_{m}\times \widetilde{B}_{N-2m}$
.
By Proposition 3.2, we have that
Since Fourier transform commutes with induction (see (2.11)), it suffices to show that the Fourier transform of
![]() $\operatorname{IC}(\mathfrak{l}_{1},{\mathcal{K}}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}))$
is supported on an
$\operatorname{IC}(\mathfrak{l}_{1},{\mathcal{K}}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D708}}\boxtimes V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}))$
is supported on an
![]() $L_{K}$
-nilpotent orbit in
$L_{K}$
-nilpotent orbit in
![]() $\mathfrak{l}_{1}$
. This follows from the classical Springer correspondence for
$\mathfrak{l}_{1}$
. This follows from the classical Springer correspondence for
![]() $\mathfrak{gl}(m)$
and (4.8) applied to the symmetric pair
$\mathfrak{gl}(m)$
and (4.8) applied to the symmetric pair
![]() $(\text{SL}(N-2m),\text{SO}(N-2m))$
(see (3.8)).
$(\text{SL}(N-2m),\text{SO}(N-2m))$
(see (3.8)).
The proof for
![]() $\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})$
,
$\operatorname{IC}(\mathfrak{g}_{1}^{m},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})$
,
![]() $\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}})$
proceeds in the same manner; in the latter case one uses the corresponding
$\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset )^{\unicode[STIX]{x1D714}})$
proceeds in the same manner; in the latter case one uses the corresponding
![]() $\unicode[STIX]{x1D703}$
-stable Levi and parabolic subgroups. We omit the details.◻
$\unicode[STIX]{x1D703}$
-stable Levi and parabolic subgroups. We omit the details.◻
4.2 More on induction
Let
![]() $(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
. Assume that
$(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{N}$
. Assume that
![]() $|\unicode[STIX]{x1D708}|=m>0$
. Let
$|\unicode[STIX]{x1D708}|=m>0$
. Let
![]() $L^{m}\subset P^{m}$
be as in §3. Recall that
$L^{m}\subset P^{m}$
be as in §3. Recall that
![]() $L_{K}^{m}\cong \text{GL}(m)\times \text{SO}(N-2m)$
and
$L_{K}^{m}\cong \text{GL}(m)\times \text{SO}(N-2m)$
and
![]() $\mathfrak{l}_{1}^{m}\cong \mathfrak{gl}(m)\oplus \mathfrak{sl}(N-2m)_{1}$
.
$\mathfrak{l}_{1}^{m}\cong \mathfrak{gl}(m)\oplus \mathfrak{sl}(N-2m)_{1}$
.
A nilpotent
![]() $L_{K}^{m}$
-orbit in
$L_{K}^{m}$
-orbit in
![]() $\mathfrak{l}_{1}^{m}$
is given by a nilpotent orbit in
$\mathfrak{l}_{1}^{m}$
is given by a nilpotent orbit in
![]() $\mathfrak{gl}(m)$
and a nilpotent
$\mathfrak{gl}(m)$
and a nilpotent
![]() $\text{SO}(N-2m)$
-orbit in
$\text{SO}(N-2m)$
-orbit in
![]() $\mathfrak{sl}(N-2m)_{1}$
. Thus the nilpotent
$\mathfrak{sl}(N-2m)_{1}$
. Thus the nilpotent
![]() $L_{K}^{m}$
-orbits in
$L_{K}^{m}$
-orbits in
![]() $\mathfrak{l}_{1}^{m}$
are parametrized by
$\mathfrak{l}_{1}^{m}$
are parametrized by
![]() ${\mathcal{P}}(m)\times {\mathcal{P}}(N-2m)$
, with extra labels
${\mathcal{P}}(m)\times {\mathcal{P}}(N-2m)$
, with extra labels
![]() $\text{I}$
and
$\text{I}$
and
![]() $\text{II}$
for partitions in
$\text{II}$
for partitions in
![]() ${\mathcal{P}}(N-2m)$
with all parts even. For
${\mathcal{P}}(N-2m)$
with all parts even. For
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{P}}(m)$
and
$\unicode[STIX]{x1D6FC}\in {\mathcal{P}}(m)$
and
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{P}}(N-2m)$
, we denote by
$\unicode[STIX]{x1D6FD}\in {\mathcal{P}}(N-2m)$
, we denote by
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
(or
${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
(or
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
) the nilpotent
${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
) the nilpotent
![]() $L_{K}^{m}$
-orbit in
$L_{K}^{m}$
-orbit in
![]() $\mathfrak{l}_{1}^{m}$
given by the nilpotent orbit
$\mathfrak{l}_{1}^{m}$
given by the nilpotent orbit
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FC}}$
in
${\mathcal{O}}_{\unicode[STIX]{x1D6FC}}$
in
![]() $\mathfrak{gl}(m)$
and the nilpotent
$\mathfrak{gl}(m)$
and the nilpotent
![]() $\text{SO}(N-2m)$
-orbit
$\text{SO}(N-2m)$
-orbit
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FD}}$
(or
${\mathcal{O}}_{\unicode[STIX]{x1D6FD}}$
(or
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
) in
${\mathcal{O}}_{\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
) in
![]() $\mathfrak{sl}(N-2m)_{1}$
.
$\mathfrak{sl}(N-2m)_{1}$
.
In the following we will omit the labels
![]() $\text{I}$
and
$\text{I}$
and
![]() $\text{II}$
with the understanding that everything should have corresponding labels, for example,
$\text{II}$
with the understanding that everything should have corresponding labels, for example,
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
etc.
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
etc.
Proposition 4.4. Let
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{P}}(m)$
and
$\unicode[STIX]{x1D6FC}\in {\mathcal{P}}(m)$
and
![]() $\unicode[STIX]{x1D6FD}\in {\mathcal{P}}(N-2m)$
. Let
$\unicode[STIX]{x1D6FD}\in {\mathcal{P}}(N-2m)$
. Let
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
, i.e.,
${\mathcal{O}}_{\unicode[STIX]{x1D706}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
, i.e.,
![]() $\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D6FD}_{i}+2\unicode[STIX]{x1D6FC}_{i}$
. Assume that
$\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D6FD}_{i}+2\unicode[STIX]{x1D6FC}_{i}$
. Assume that
![]() $u\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
and
$u\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
and
![]() $v\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}\cap (u+(\mathfrak{n}_{P^{m}})_{1})$
. We have a natural surjective map
$v\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}\cap (u+(\mathfrak{n}_{P^{m}})_{1})$
. We have a natural surjective map
Moreover, let
![]() $\mathbb{C}\boxtimes {\mathcal{E}}$
be an
$\mathbb{C}\boxtimes {\mathcal{E}}$
be an
![]() $L_{K}^{m}$
-equivariant irreducible local system on
$L_{K}^{m}$
-equivariant irreducible local system on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
and let
${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
and let
![]() $\tilde{{\mathcal{E}}}$
be the
$\tilde{{\mathcal{E}}}$
be the
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
obtained from
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
obtained from
![]() $\mathbb{C}\boxtimes {\mathcal{E}}$
via the map
$\mathbb{C}\boxtimes {\mathcal{E}}$
via the map
![]() $\unicode[STIX]{x1D713}$
above. Then
$\unicode[STIX]{x1D713}$
above. Then
![]() $\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},\tilde{{\mathcal{E}}})$
is a direct summand of
$\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},\tilde{{\mathcal{E}}})$
is a direct summand of
![]() $\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D707}},\mathbb{C}\boxtimes {\mathcal{E}})$
.
$\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D708},\unicode[STIX]{x1D707}},\mathbb{C}\boxtimes {\mathcal{E}})$
.
Corollary 4.5. If moreover
![]() $({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{E}})\in {\mathcal{A}}_{N-2m}$
is a pair such that
$({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{E}})\in {\mathcal{A}}_{N-2m}$
is a pair such that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{E}}))$
has full support, then we have
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{E}}))$
has full support, then we have
As before let us now write
![]() $L=L^{m}$
and
$L=L^{m}$
and
![]() $P=P^{m}$
etc. We begin the proof of the above proposition with the following lemma.
$P=P^{m}$
etc. We begin the proof of the above proposition with the following lemma.
Lemma 4.6. The map
is generically one-to-one.
Proof. Let
![]() $x_{0}\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}$
. We can and will assume that
$x_{0}\in {\mathcal{O}}_{\unicode[STIX]{x1D706}}$
. We can and will assume that
![]() $x_{0}\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}+(\mathfrak{n}_{P})_{1}$
. We show that
$x_{0}\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}+(\mathfrak{n}_{P})_{1}$
. We show that
![]() $\unicode[STIX]{x1D6FE}^{-1}(x_{0})$
is a point. Assume that
$\unicode[STIX]{x1D6FE}^{-1}(x_{0})$
is a point. Assume that
![]() $\unicode[STIX]{x1D6FE}(k,x)=x_{0}$
, i.e.,
$\unicode[STIX]{x1D6FE}(k,x)=x_{0}$
, i.e.,
![]() $\operatorname{Ad}k(x)=x_{0}$
. Then
$\operatorname{Ad}k(x)=x_{0}$
. Then
![]() $x\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}+(\mathfrak{n}_{P})_{1}$
. Let
$x\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}+(\mathfrak{n}_{P})_{1}$
. Let
![]() $\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D706}}$
(respectively
$\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D706}}$
(respectively
![]() $\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
) be the (unique)
$\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
) be the (unique)
![]() $G$
-orbit (respectively
$G$
-orbit (respectively
![]() $L$
-orbit) in
$L$
-orbit) in
![]() $\mathfrak{g}$
(respectively
$\mathfrak{g}$
(respectively
![]() $\mathfrak{l}$
) that contains
$\mathfrak{l}$
) that contains
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
). We have that
${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
). We have that
in the notation of Lusztig and Spaltenstein [Reference Lusztig and SpaltensteinLS79]. By [Reference Lusztig and SpaltensteinLS79, Theorem 1.3], we have
![]() $Z_{G}^{0}(x_{0})\subset P$
. In fact, we have that
$Z_{G}^{0}(x_{0})\subset P$
. In fact, we have that
![]() $Z_{G}(x_{0})\subset P$
. This can be seen by enlarging the group
$Z_{G}(x_{0})\subset P$
. This can be seen by enlarging the group
![]() $G$
to
$G$
to
![]() $\text{GL}(N)$
and using the fact that
$\text{GL}(N)$
and using the fact that
![]() $Z_{\text{GL}(N)}(x_{0})$
is connected. Thus
$Z_{\text{GL}(N)}(x_{0})$
is connected. Thus
![]() $Z_{K}(x_{0})\subset P_{K}$
. Furthermore,
$Z_{K}(x_{0})\subset P_{K}$
. Furthermore,
![]() $\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D706}}\cap (\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}+\mathfrak{n}_{P})$
is a single orbit under
$\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D706}}\cap (\widetilde{{\mathcal{O}}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}+\mathfrak{n}_{P})$
is a single orbit under
![]() $P$
. Thus there exists
$P$
. Thus there exists
![]() $p\in P$
such that
$p\in P$
such that
![]() $\operatorname{Ad}p(x)=x_{0}$
. It follows that
$\operatorname{Ad}p(x)=x_{0}$
. It follows that
![]() $k^{-1}p\in Z_{G}(x_{0})\subset P$
. Thus
$k^{-1}p\in Z_{G}(x_{0})\subset P$
. Thus
![]() $k\in P\cap K=P_{K}$
. Now we have that
$k\in P\cap K=P_{K}$
. Now we have that
![]() $(k,x)=(1,\operatorname{Ad}k(x))=(1,x_{0})$
.◻
$(k,x)=(1,\operatorname{Ad}k(x))=(1,x_{0})$
.◻
Proof of Proposition 4.4.
Note that the proof of the above lemma shows that
![]() $Z_{G}(v)=Z_{P}(v)$
. We have
$Z_{G}(v)=Z_{P}(v)$
. We have
![]() $Z_{P}(v)\subset Z_{L}(u)U_{P}$
. Thus
$Z_{P}(v)\subset Z_{L}(u)U_{P}$
. Thus
![]() $Z_{K}(v)=Z_{P_{K}}(v)\subset Z_{L_{K}}(u)(U_{P}\cap K)$
. It follows that we have a natural projection map
$Z_{K}(v)=Z_{P_{K}}(v)\subset Z_{L_{K}}(u)(U_{P}\cap K)$
. It follows that we have a natural projection map
We show that this gives us the desired map
![]() $\unicode[STIX]{x1D713}$
. Following [Reference Lusztig and SpaltensteinLS79], we have that
$\unicode[STIX]{x1D713}$
. Following [Reference Lusztig and SpaltensteinLS79], we have that
![]() $Z_{L_{K}}(u)(U_{P}\cap K)$
has a dense orbit, i.e., the orbit of
$Z_{L_{K}}(u)(U_{P}\cap K)$
has a dense orbit, i.e., the orbit of
![]() $v$
, in the irreducible variety
$v$
, in the irreducible variety
![]() $u+(\mathfrak{n}_{P})_{1}$
. Thus
$u+(\mathfrak{n}_{P})_{1}$
. Thus
![]() $Z_{P_{K}}(v)=Z_{K}(v)$
meets all the irreducible components of
$Z_{P_{K}}(v)=Z_{K}(v)$
meets all the irreducible components of
![]() $Z_{L_{K}}(u)(U_{P}\cap K)$
, which implies that
$Z_{L_{K}}(u)(U_{P}\cap K)$
, which implies that
![]() $\unicode[STIX]{x1D713}$
is surjective.
$\unicode[STIX]{x1D713}$
is surjective.
It is easy to see that
The proposition follows from the definition of parabolic induction functor and Lemma 4.6.◻
Remark 4.7. The proof of Lemma 4.6 and the existence and surjectivity of the map
![]() $\unicode[STIX]{x1D713}$
in Proposition 4.4 works for any
$\unicode[STIX]{x1D713}$
in Proposition 4.4 works for any
![]() $\unicode[STIX]{x1D703}$
-stable Levi contained in a
$\unicode[STIX]{x1D703}$
-stable Levi contained in a
![]() $\unicode[STIX]{x1D703}$
-stable parabolic subgroup.
$\unicode[STIX]{x1D703}$
-stable parabolic subgroup.
Proof of Corollary 4.5.
Note that the assumption implies that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}},\mathbb{C}\boxtimes {\mathcal{E}}))$
has full support, i.e.,
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}},\mathbb{C}\boxtimes {\mathcal{E}}))$
has full support, i.e.,
![]() $\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}},\mathbb{C}\boxtimes {\mathcal{E}})=\operatorname{IC}(\mathfrak{l}_{1},{\mathcal{G}})$
for some irreducible
$\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}},\mathbb{C}\boxtimes {\mathcal{E}})=\operatorname{IC}(\mathfrak{l}_{1},{\mathcal{G}})$
for some irreducible
![]() $L_{K}$
-equivariant local system
$L_{K}$
-equivariant local system
![]() ${\mathcal{G}}$
on
${\mathcal{G}}$
on
![]() $\mathfrak{l}_{1}^{\text{rs}}$
. We have that
$\mathfrak{l}_{1}^{\text{rs}}$
. We have that
It suffices to show that
![]() $\operatorname{Ind}_{\mathfrak{l}_{1}\subset \mathfrak{p}_{1}}^{\mathfrak{g}_{1}}\operatorname{IC}(\mathfrak{l}_{1},{\mathcal{G}})$
is irreducible. This follows from the definition of the induction functor and Proposition 3.1.◻
$\operatorname{Ind}_{\mathfrak{l}_{1}\subset \mathfrak{p}_{1}}^{\mathfrak{g}_{1}}\operatorname{IC}(\mathfrak{l}_{1},{\mathcal{G}})$
is irreducible. This follows from the definition of the induction functor and Proposition 3.1.◻
Corollary 4.8. The Fourier transform of a nilpotent orbital complex
![]() $\operatorname{IC}({\mathcal{O}},{\mathcal{E}})\in {\mathcal{A}}_{N}$
has full support, i.e.,
$\operatorname{IC}({\mathcal{O}},{\mathcal{E}})\in {\mathcal{A}}_{N}$
has full support, i.e.,
![]() $\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}},{\mathcal{E}}))=\mathfrak{g}_{1}$
, if and only if it is not of the form
$\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}},{\mathcal{E}}))=\mathfrak{g}_{1}$
, if and only if it is not of the form
![]() $\operatorname{Ind}_{\mathfrak{l}_{1}\subset \mathfrak{p}_{1}}^{\mathfrak{g}_{1}}\operatorname{IC}({\mathcal{O}}^{\prime },{\mathcal{E}}^{\prime })$
where
$\operatorname{Ind}_{\mathfrak{l}_{1}\subset \mathfrak{p}_{1}}^{\mathfrak{g}_{1}}\operatorname{IC}({\mathcal{O}}^{\prime },{\mathcal{E}}^{\prime })$
where
![]() $\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}^{\prime },{\mathcal{E}}^{\prime }))=\mathfrak{l}_{1}$
, and
$\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}^{\prime },{\mathcal{E}}^{\prime }))=\mathfrak{l}_{1}$
, and
![]() $L\subset P$
is a pair chosen as in §3.
$L\subset P$
is a pair chosen as in §3.
Proof. The only if part follows from the facts that Fourier transform commutes with parabolic induction and that
![]() $\operatorname{supp}\operatorname{Ind}_{\mathfrak{l}_{1}\subset \mathfrak{p}_{1}}^{\mathfrak{g}_{1}}A\subsetneq \mathfrak{g}_{1}$
. The if part follows from (4.11), Corollary 4.5 and Theorem 4.1.◻
$\operatorname{supp}\operatorname{Ind}_{\mathfrak{l}_{1}\subset \mathfrak{p}_{1}}^{\mathfrak{g}_{1}}A\subsetneq \mathfrak{g}_{1}$
. The if part follows from (4.11), Corollary 4.5 and Theorem 4.1.◻
Corollary 4.9. Let
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \,)\in {\mathcal{P}}(N)$
.
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \,)\in {\mathcal{P}}(N)$
.
(1) If
 $\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\geqslant 3$
for some
$\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\geqslant 3$
for some
 $i$
, then
$i$
, then
 $\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))\neq \mathfrak{g}_{1}$
for any
$\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))\neq \mathfrak{g}_{1}$
for any
 $K$
-equivariant local system
$K$
-equivariant local system
 ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
. The same holds for
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
. The same holds for
 ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
if
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
if
 $\unicode[STIX]{x1D706}$
has only even parts.
$\unicode[STIX]{x1D706}$
has only even parts.(2) Suppose that
 $\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 2$
for all
$\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 2$
for all
 $i$
. Let
$i$
. Let
 $f_{\unicode[STIX]{x1D706}}$
be the number of different sizes of parts of
$f_{\unicode[STIX]{x1D706}}$
be the number of different sizes of parts of
 $\unicode[STIX]{x1D706}$
, and
$\unicode[STIX]{x1D706}$
, and
 $g_{\unicode[STIX]{x1D706}}$
the number of
$g_{\unicode[STIX]{x1D706}}$
the number of
 $i$
such that
$i$
such that
 $\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}=2$
.
$\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}=2$
.(a) If at least one part of
 $\unicode[STIX]{x1D706}$
is odd, then there are
$\unicode[STIX]{x1D706}$
is odd, then there are
 $2^{f_{\unicode[STIX]{x1D706}}-1-g_{\unicode[STIX]{x1D706}}}$
irreducible
$2^{f_{\unicode[STIX]{x1D706}}-1-g_{\unicode[STIX]{x1D706}}}$
irreducible
 $K$
-equivariant local systems
$K$
-equivariant local systems
 ${\mathcal{E}}$
on
${\mathcal{E}}$
on
 ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
such that
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
such that
 $\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))=\mathfrak{g}_{1}$
.
$\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))=\mathfrak{g}_{1}$
.(b) If all parts of
 $\unicode[STIX]{x1D706}$
are even, then there is exactly one irreducible
$\unicode[STIX]{x1D706}$
are even, then there is exactly one irreducible
 $K$
-equivariant local system
$K$
-equivariant local system
 ${\mathcal{E}}^{\unicode[STIX]{x1D714}}$
on each orbit
${\mathcal{E}}^{\unicode[STIX]{x1D714}}$
on each orbit
 ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
 $\unicode[STIX]{x1D714}=\text{I},\text{II}$
, such that
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
, such that
 $\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},{\mathcal{E}}^{\unicode[STIX]{x1D714}}))=\mathfrak{g}_{1}$
.
$\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},{\mathcal{E}}^{\unicode[STIX]{x1D714}}))=\mathfrak{g}_{1}$
.
In particular, if
![]() $\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 1$
for all
$\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 1$
for all
![]() $i$
, then
$i$
, then
![]() $\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))=\mathfrak{g}_{1}$
for any
$\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))=\mathfrak{g}_{1}$
for any
![]() $K$
-equivariant local system
$K$
-equivariant local system
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
.
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
.
Proof. (1) Assume that
![]() $\unicode[STIX]{x1D706}_{i_{0}}-\unicode[STIX]{x1D706}_{i_{0}+1}\geqslant 3$
. Let
$\unicode[STIX]{x1D706}_{i_{0}}-\unicode[STIX]{x1D706}_{i_{0}+1}\geqslant 3$
. Let
![]() $m=i_{0}$
,
$m=i_{0}$
,
![]() $\unicode[STIX]{x1D6FC}=1^{i_{0}}$
,
$\unicode[STIX]{x1D6FC}=1^{i_{0}}$
,
![]() $\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D706}_{1}-2,\ldots ,\unicode[STIX]{x1D706}_{i_{0}}-2,\unicode[STIX]{x1D706}_{i_{0}+1},\ldots )$
. Then
$\unicode[STIX]{x1D6FD}=(\unicode[STIX]{x1D706}_{1}-2,\ldots ,\unicode[STIX]{x1D706}_{i_{0}}-2,\unicode[STIX]{x1D706}_{i_{0}+1},\ldots )$
. Then
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
. Let
${\mathcal{O}}_{\unicode[STIX]{x1D706}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
. Let
![]() $u\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
and
$u\in {\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
and
![]() $v\,\in \,{\mathcal{O}}_{\unicode[STIX]{x1D706}}\cap (u+(\mathfrak{n}_{P^{m}})_{1})$
. Note that
$v\,\in \,{\mathcal{O}}_{\unicode[STIX]{x1D706}}\cap (u+(\mathfrak{n}_{P^{m}})_{1})$
. Note that
![]() $A_{K}(v)\cong A_{L_{K}^{m}}(u)$
. It then follows from Proposition 4.4 that for each irreducible
$A_{K}(v)\cong A_{L_{K}^{m}}(u)$
. It then follows from Proposition 4.4 that for each irreducible
![]() $K$
-equivariant local system
$K$
-equivariant local system
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
,
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
,
![]() $\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}})$
is a direct summand of
$\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}})$
is a direct summand of
![]() $\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}},{\mathcal{E}}_{0})$
for some irreducible
$\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}},{\mathcal{E}}_{0})$
for some irreducible
![]() $L_{K}$
-equivariant local system
$L_{K}$
-equivariant local system
![]() ${\mathcal{E}}_{0}$
on
${\mathcal{E}}_{0}$
on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
. As before, this shows that
${\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
. As before, this shows that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))$
has smaller support.
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))$
has smaller support.
In the case when
![]() $\unicode[STIX]{x1D706}$
has only even parts, we let
$\unicode[STIX]{x1D706}$
has only even parts, we let
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
, if
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{m}\subset \mathfrak{p}_{1}^{m}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}^{\unicode[STIX]{x1D714}}$
, if
![]() $m<N/2$
, and we let
$m<N/2$
, and we let
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{n,\unicode[STIX]{x1D714}}\subset \mathfrak{p}_{1}^{n,\unicode[STIX]{x1D714}}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
, if
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}=\operatorname{Ind}_{\mathfrak{l}_{1}^{n,\unicode[STIX]{x1D714}}\subset \mathfrak{p}_{1}^{n,\unicode[STIX]{x1D714}}}^{\mathfrak{g}_{1}}{\mathcal{O}}_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
, if
![]() $m=N/2=n$
, where
$m=N/2=n$
, where
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
. The proof for
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
. The proof for
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
then proceeds in the same way.
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
then proceeds in the same way.
(2) We argue by induction on
![]() $g_{\unicode[STIX]{x1D706}}$
. If
$g_{\unicode[STIX]{x1D706}}$
. If
![]() $g_{\unicode[STIX]{x1D706}}=0$
, then (2) follows from (4.12) and Corollary 4.8. Assume by induction hypothesis that (2) holds for all
$g_{\unicode[STIX]{x1D706}}=0$
, then (2) follows from (4.12) and Corollary 4.8. Assume by induction hypothesis that (2) holds for all
![]() $\unicode[STIX]{x1D707}$
with
$\unicode[STIX]{x1D707}$
with
![]() $g_{\unicode[STIX]{x1D707}}<g_{\unicode[STIX]{x1D706}}$
.
$g_{\unicode[STIX]{x1D707}}<g_{\unicode[STIX]{x1D706}}$
.
Assume first that
![]() $\unicode[STIX]{x1D706}$
has at least one odd part. Suppose that
$\unicode[STIX]{x1D706}$
has at least one odd part. Suppose that
![]() $i_{1},\ldots ,i_{k}$
are such that
$i_{1},\ldots ,i_{k}$
are such that
![]() $\unicode[STIX]{x1D706}_{i_{j}}-\unicode[STIX]{x1D706}_{i_{j}+1}=2$
, where
$\unicode[STIX]{x1D706}_{i_{j}}-\unicode[STIX]{x1D706}_{i_{j}+1}=2$
, where
![]() $k=g_{\unicode[STIX]{x1D706}}$
.
$k=g_{\unicode[STIX]{x1D706}}$
.
Let
![]() $a=(a_{1}\geqslant a_{2}\geqslant \cdots \geqslant a_{k}\geqslant 0)$
be a partition such that
$a=(a_{1}\geqslant a_{2}\geqslant \cdots \geqslant a_{k}\geqslant 0)$
be a partition such that
![]() $a\neq \emptyset$
,
$a\neq \emptyset$
,
![]() $a_{k}\leqslant 1$
, and
$a_{k}\leqslant 1$
, and
![]() $a_{l}\leqslant a_{l+1}-1$
. Note that the number of such partitions is
$a_{l}\leqslant a_{l+1}-1$
. Note that the number of such partitions is
![]() $2^{k}-1$
. Consider a partition
$2^{k}-1$
. Consider a partition
![]() $\unicode[STIX]{x1D707}(a)$
such that
$\unicode[STIX]{x1D707}(a)$
such that
![]() $\unicode[STIX]{x1D707}_{l}=\unicode[STIX]{x1D706}_{l}\,-\,2a_{j}$
for
$\unicode[STIX]{x1D707}_{l}=\unicode[STIX]{x1D706}_{l}\,-\,2a_{j}$
for
![]() $l\in [i_{j-1}+1,i_{j}]$
. Then
$l\in [i_{j-1}+1,i_{j}]$
. Then
![]() $\unicode[STIX]{x1D707}(a)$
satisfies that
$\unicode[STIX]{x1D707}(a)$
satisfies that
![]() $\unicode[STIX]{x1D707}(a)_{i}-\unicode[STIX]{x1D707}(a)_{i+1}\leqslant 2$
and
$\unicode[STIX]{x1D707}(a)_{i}-\unicode[STIX]{x1D707}(a)_{i+1}\leqslant 2$
and
![]() $g_{\unicode[STIX]{x1D707}(a)}<g_{\unicode[STIX]{x1D706}}$
. Moreover,
$g_{\unicode[STIX]{x1D707}(a)}<g_{\unicode[STIX]{x1D706}}$
. Moreover,
![]() $\unicode[STIX]{x1D707}$
has at least one odd part, and
$\unicode[STIX]{x1D707}$
has at least one odd part, and
![]() $f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}=f_{\unicode[STIX]{x1D707}(a)}-g_{\unicode[STIX]{x1D707}(a)}$
. Let
$f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}=f_{\unicode[STIX]{x1D707}(a)}-g_{\unicode[STIX]{x1D707}(a)}$
. Let
![]() $m=\sum _{j=1}^{k}i_{j}$
. We have that
$m=\sum _{j=1}^{k}i_{j}$
. We have that
By induction hypothesis, there are
![]() $2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}-1}$
irreducible
$2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}-1}$
irreducible
![]() $K$
-equivariant local systems
$K$
-equivariant local systems
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
![]() ${\mathcal{O}}_{a,\unicode[STIX]{x1D707}(a)}$
such that
${\mathcal{O}}_{a,\unicode[STIX]{x1D707}(a)}$
such that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{a,\unicode[STIX]{x1D707}(a)},{\mathcal{E}})$
has full support. By Corollary 4.5, we have that
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{a,\unicode[STIX]{x1D707}(a)},{\mathcal{E}})$
has full support. By Corollary 4.5, we have that
This gives rise to
![]() $(2^{k}-1)\cdot 2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}-1}=2^{f_{\unicode[STIX]{x1D706}}-1}-2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}-1}$
irreducible
$(2^{k}-1)\cdot 2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}-1}=2^{f_{\unicode[STIX]{x1D706}}-1}-2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}-1}$
irreducible
![]() $K$
-equivariant local systems
$K$
-equivariant local systems
![]() $\tilde{{\mathcal{E}}}$
on
$\tilde{{\mathcal{E}}}$
on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
such that
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
such that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},\tilde{{\mathcal{E}}})$
has smaller support (with
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},\tilde{{\mathcal{E}}})$
has smaller support (with
![]() $a$
varying).
$a$
varying).
The case when all parts of
![]() $\unicode[STIX]{x1D706}$
even can be argued in the same way. Note that in this case
$\unicode[STIX]{x1D706}$
even can be argued in the same way. Note that in this case
![]() $g_{\unicode[STIX]{x1D706}}=f_{\unicode[STIX]{x1D706}}$
.
$g_{\unicode[STIX]{x1D706}}=f_{\unicode[STIX]{x1D706}}$
.
Let us write
![]() $m_{\unicode[STIX]{x1D706}}$
(respectively
$m_{\unicode[STIX]{x1D706}}$
(respectively
![]() $m_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
$m_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
) for the number of irreducible
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
) for the number of irreducible
![]() $K$
-equivariant local systems
$K$
-equivariant local systems
![]() $\tilde{{\mathcal{E}}}$
on
$\tilde{{\mathcal{E}}}$
on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
) such that
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
) such that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},\tilde{{\mathcal{E}}})$
(respectively
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},\tilde{{\mathcal{E}}})$
(respectively
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},\tilde{{\mathcal{E}}})$
) has full support when at least one part of
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},\tilde{{\mathcal{E}}})$
) has full support when at least one part of
![]() $\unicode[STIX]{x1D706}$
is odd (respectively when all parts of
$\unicode[STIX]{x1D706}$
is odd (respectively when all parts of
![]() $\unicode[STIX]{x1D706}$
are even).
$\unicode[STIX]{x1D706}$
are even).
We conclude from the discussion above that
Theorem 4.1 implies that the number of pairs
![]() $\operatorname{IC}({\mathcal{O}},{\mathcal{E}})\in {\mathcal{A}}_{N}$
such that
$\operatorname{IC}({\mathcal{O}},{\mathcal{E}})\in {\mathcal{A}}_{N}$
such that
![]() $\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}},{\mathcal{E}}))=\mathfrak{g}_{1}$
is
$\operatorname{supp}\mathfrak{F}(\operatorname{IC}({\mathcal{O}},{\mathcal{E}}))=\mathfrak{g}_{1}$
is
![]() $d(n)$
(see (4.1)), when
$d(n)$
(see (4.1)), when
![]() $N=2n+1$
, and
$N=2n+1$
, and
![]() $e(n)$
(see (4.2)), when
$e(n)$
(see (4.2)), when
![]() $N=2n$
. In view of (4.13) and claim (1) of the corollary, it suffices to show that
$N=2n$
. In view of (4.13) and claim (1) of the corollary, it suffices to show that
This can be seen as follows. Note that when
![]() $N$
is even, the number of orbits of the form
$N$
is even, the number of orbits of the form
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
, where all parts of
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
, where all parts of
![]() $\unicode[STIX]{x1D706}$
are even and
$\unicode[STIX]{x1D706}$
are even and
![]() $\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 2$
, is
$\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 2$
, is
![]() $2q(n)$
. We know that
$2q(n)$
. We know that
A partition
![]() $\unicode[STIX]{x1D706}$
satisfies that
$\unicode[STIX]{x1D706}$
satisfies that
![]() $\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 2$
if and only if each part of the transpose partition
$\unicode[STIX]{x1D706}_{i}-\unicode[STIX]{x1D706}_{i+1}\leqslant 2$
if and only if each part of the transpose partition
![]() $\unicode[STIX]{x1D706}^{\prime }$
has multiplicity at most
$\unicode[STIX]{x1D706}^{\prime }$
has multiplicity at most
![]() $2$
. We have
$2$
. We have
![]() $f_{\unicode[STIX]{x1D706}}=f_{\unicode[STIX]{x1D706}^{\prime }}$
and
$f_{\unicode[STIX]{x1D706}}=f_{\unicode[STIX]{x1D706}^{\prime }}$
and
![]() $g_{\unicode[STIX]{x1D706}}$
equals the number of parts in
$g_{\unicode[STIX]{x1D706}}$
equals the number of parts in
![]() $\unicode[STIX]{x1D706}^{\prime }$
with multiplicity
$\unicode[STIX]{x1D706}^{\prime }$
with multiplicity
![]() $2$
. It is easy to see that each
$2$
. It is easy to see that each
![]() $\unicode[STIX]{x1D706}^{\prime }$
whose parts have multiplicity at most
$\unicode[STIX]{x1D706}^{\prime }$
whose parts have multiplicity at most
![]() $2$
appears in
$2$
appears in
![]() $\prod _{s\geqslant 1}(1+x^{s})^{2}$
exactly
$\prod _{s\geqslant 1}(1+x^{s})^{2}$
exactly
![]() $2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}}$
times. Hence (4.14) follows.◻
$2^{f_{\unicode[STIX]{x1D706}}-g_{\unicode[STIX]{x1D706}}}$
times. Hence (4.14) follows.◻
Remark 4.10. In [Reference Chen, Vilonen and XueCVX15a, Conjecture 1.2], we conjectured that one can obtain all nilpotent orbital complexes by induction from those of smaller groups whose Fourier transforms have full support. This conjecture follows from Corollary 4.8.
5 Cohomology of Hessenberg varieties
Hessenberg varieties, defined generally in [Reference Goresky, Kottwitz and MacPhersonGKM06], arise naturally in our setting (for details, see [Reference Chen, Vilonen and XueCVX15b]). In particular, they arise as fibers of maps
![]() $\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}$
and
![]() $\check{\unicode[STIX]{x1D70B}}$
in the following diagram
$\check{\unicode[STIX]{x1D70B}}$
in the following diagram

where
![]() $P_{K}=P\cap K$
for a
$P_{K}=P\cap K$
for a
![]() $\unicode[STIX]{x1D703}$
-stable parabolic subgroup
$\unicode[STIX]{x1D703}$
-stable parabolic subgroup
![]() $P$
of
$P$
of
![]() $G$
,
$G$
,
![]() $E$
is a
$E$
is a
![]() $P_{K}$
-stable subspace of
$P_{K}$
-stable subspace of
![]() $\mathfrak{g}_{1}$
consisting of nilpotent elements, and
$\mathfrak{g}_{1}$
consisting of nilpotent elements, and
![]() $E^{\bot }$
is the orthogonal complement of
$E^{\bot }$
is the orthogonal complement of
![]() $E$
in
$E$
in
![]() $\mathfrak{g}_{1}$
via a
$\mathfrak{g}_{1}$
via a
![]() $K$
-invariant non-degenerate form on
$K$
-invariant non-degenerate form on
![]() $\mathfrak{g}_{1}$
. The generic fibers of maps
$\mathfrak{g}_{1}$
. The generic fibers of maps
![]() $\check{\unicode[STIX]{x1D70B}}$
are Hessenberg varieties.
$\check{\unicode[STIX]{x1D70B}}$
are Hessenberg varieties.
In this section we discuss an application of our result to cohomology of Hessenberg varieties. Let us fix
![]() $s\in \mathfrak{g}_{1}^{\text{rs}}$
and consider the corresponding Hessenberg variety
$s\in \mathfrak{g}_{1}^{\text{rs}}$
and consider the corresponding Hessenberg variety
The centralizer
![]() $Z_{K}(s)$
acts naturally on
$Z_{K}(s)$
acts naturally on
![]() $\operatorname{Hess}$
and it induces an action of the component group
$\operatorname{Hess}$
and it induces an action of the component group
![]() $\unicode[STIX]{x1D70B}_{0}(Z_{K}(s))\cong I_{N}$
on the cohomology groups
$\unicode[STIX]{x1D70B}_{0}(Z_{K}(s))\cong I_{N}$
on the cohomology groups
![]() $H^{\ast }(\operatorname{Hess},\mathbb{C})$
. Let
$H^{\ast }(\operatorname{Hess},\mathbb{C})$
. Let
be the eigenspace decomposition with respect to the action of
![]() $I_{N}$
.
$I_{N}$
.
Definition 5.1. The stable part
![]() $\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\operatorname{st}}$
of
$\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\operatorname{st}}$
of
![]() $\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})$
is the direct summand
$\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})$
is the direct summand
![]() $\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{\operatorname{triv}}}$
where
$\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{\operatorname{triv}}}$
where
![]() $\unicode[STIX]{x1D712}_{\operatorname{triv}}\in I_{N}^{\vee }$
is the trivial character.
$\unicode[STIX]{x1D712}_{\operatorname{triv}}\in I_{N}^{\vee }$
is the trivial character.
For simplicity we now assume
![]() $\check{\unicode[STIX]{x1D70B}}$
is onto. In this case
$\check{\unicode[STIX]{x1D70B}}$
is onto. In this case
![]() $\check{\unicode[STIX]{x1D70B}}$
is smooth over
$\check{\unicode[STIX]{x1D70B}}$
is smooth over
![]() $\mathfrak{g}_{1}^{\text{rs}}$
(e.g. see [Reference Chen, Vilonen and XueCVX15b, Lemma 2.1]) and the equivariant fundamental group
$\mathfrak{g}_{1}^{\text{rs}}$
(e.g. see [Reference Chen, Vilonen and XueCVX15b, Lemma 2.1]) and the equivariant fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)\cong I_{N}\rtimes B_{N}$
acts on
$\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)\cong I_{N}\rtimes B_{N}$
acts on
![]() $H^{\ast }(\operatorname{Hess},\mathbb{C})$
by the monodromy action. Recall that for
$H^{\ast }(\operatorname{Hess},\mathbb{C})$
by the monodromy action. Recall that for
![]() $\unicode[STIX]{x1D712}\in I_{N}^{\vee }$
,
$\unicode[STIX]{x1D712}\in I_{N}^{\vee }$
,
![]() $B_{\unicode[STIX]{x1D712}}$
stands for the stabilizer of
$B_{\unicode[STIX]{x1D712}}$
stands for the stabilizer of
![]() $\unicode[STIX]{x1D712}$
in
$\unicode[STIX]{x1D712}$
in
![]() $B_{N}$
. Clearly, each summand
$B_{N}$
. Clearly, each summand
![]() $H^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}}$
is stable under the action of
$H^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}}$
is stable under the action of
![]() $B_{\unicode[STIX]{x1D712}}$
. Let
$B_{\unicode[STIX]{x1D712}}$
. Let
![]() $\unicode[STIX]{x1D712}_{m}\in I_{N}^{\vee }$
,
$\unicode[STIX]{x1D712}_{m}\in I_{N}^{\vee }$
,
![]() $B_{\unicode[STIX]{x1D712}_{m}}$
, and
$B_{\unicode[STIX]{x1D712}_{m}}$
, and
![]() $B_{m,N-m}$
be as in §2.3. Assume that
$B_{m,N-m}$
be as in §2.3. Assume that
![]() $\unicode[STIX]{x1D712}$
is in the
$\unicode[STIX]{x1D712}$
is in the
![]() $B_{N}$
-orbit of
$B_{N}$
-orbit of
![]() $\unicode[STIX]{x1D712}_{m}$
. Then for any
$\unicode[STIX]{x1D712}_{m}$
. Then for any
![]() $b\in B_{N}$
with
$b\in B_{N}$
with
![]() $b.\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{m}$
we have an isomorphism
$b.\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{m}$
we have an isomorphism
![]() $\unicode[STIX]{x1D704}_{b}:B_{\unicode[STIX]{x1D712}}\cong B_{\unicode[STIX]{x1D712}_{m}},u\rightarrow bub^{-1}$
. Note that
$\unicode[STIX]{x1D704}_{b}:B_{\unicode[STIX]{x1D712}}\cong B_{\unicode[STIX]{x1D712}_{m}},u\rightarrow bub^{-1}$
. Note that
![]() $\unicode[STIX]{x1D712}_{\operatorname{triv}}=\unicode[STIX]{x1D712}_{0}$
and
$\unicode[STIX]{x1D712}_{\operatorname{triv}}=\unicode[STIX]{x1D712}_{0}$
and
![]() $B_{\unicode[STIX]{x1D712}_{m}}=B_{m,N-m}$
except when
$B_{\unicode[STIX]{x1D712}_{m}}=B_{m,N-m}$
except when
![]() $N$
is even and
$N$
is even and
![]() $m=N/2$
. In that case,
$m=N/2$
. In that case,
![]() $B_{m,N-m}$
is an index-2 subgroup of
$B_{m,N-m}$
is an index-2 subgroup of
![]() $B_{\unicode[STIX]{x1D712}_{m}}$
.
$B_{\unicode[STIX]{x1D712}_{m}}$
.
Recall the algebra
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}={\mathcal{H}}_{m,-1}\otimes {\mathcal{H}}_{N-m,-1}$
and their representations
${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}={\mathcal{H}}_{m,-1}\otimes {\mathcal{H}}_{N-m,-1}$
and their representations
![]() $D_{\unicode[STIX]{x1D707}^{1}}\otimes D_{\unicode[STIX]{x1D707}^{2}}$
introduced in §2.3. Each
$D_{\unicode[STIX]{x1D707}^{1}}\otimes D_{\unicode[STIX]{x1D707}^{2}}$
introduced in §2.3. Each
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
is a quotient of the group algebra
${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
is a quotient of the group algebra
![]() $\mathbb{C}[B_{m,N-m}]$
and
$\mathbb{C}[B_{m,N-m}]$
and
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D712}_{0},-1}={\mathcal{H}}_{\unicode[STIX]{x1D712}_{\operatorname{triv}},-1}={\mathcal{H}}_{N,-1}$
is the Hecke algebra of
${\mathcal{H}}_{\unicode[STIX]{x1D712}_{0},-1}={\mathcal{H}}_{\unicode[STIX]{x1D712}_{\operatorname{triv}},-1}={\mathcal{H}}_{N,-1}$
is the Hecke algebra of
![]() $S_{N}$
at
$S_{N}$
at
![]() $q=-1$
.
$q=-1$
.
Theorem 5.2. (i) Let
![]() $\unicode[STIX]{x1D712}_{m}\in I_{N}^{\vee }$
be the representatives of
$\unicode[STIX]{x1D712}_{m}\in I_{N}^{\vee }$
be the representatives of
![]() $B_{N}$
-orbits in §2.3. To every
$B_{N}$
-orbits in §2.3. To every
![]() $\unicode[STIX]{x1D712}\in I_{N}^{\vee }$
in the orbit of
$\unicode[STIX]{x1D712}\in I_{N}^{\vee }$
in the orbit of
![]() $\unicode[STIX]{x1D712}_{m}$
and an element
$\unicode[STIX]{x1D712}_{m}$
and an element
![]() $b\in B_{N}$
satisfying
$b\in B_{N}$
satisfying
![]() $b(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}_{m}$
, the monodromy action of
$b(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}_{m}$
, the monodromy action of
![]() $b$
on
$b$
on
![]() $\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})$
induces an isomorphism
$\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})$
induces an isomorphism
![]() $\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}}\cong \operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{m}}$
compatible with the actions of
$\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}}\cong \operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{m}}$
compatible with the actions of
![]() $B_{\unicode[STIX]{x1D712}}\stackrel{\unicode[STIX]{x1D704}_{b}}{\cong }B_{\unicode[STIX]{x1D712}_{m}}$
on both sides.
$B_{\unicode[STIX]{x1D712}}\stackrel{\unicode[STIX]{x1D704}_{b}}{\cong }B_{\unicode[STIX]{x1D712}_{m}}$
on both sides.
(ii) The action of
![]() $\mathbb{C}[B_{m,N-m}]$
on
$\mathbb{C}[B_{m,N-m}]$
on
![]() $\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{m}}$
factors through the algebra
$\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{m}}$
factors through the algebra
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
and the resulting representation is a direct sum of
${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
and the resulting representation is a direct sum of
![]() $D_{\unicode[STIX]{x1D707}^{1}}\otimes D_{\unicode[STIX]{x1D707}^{2}}$
,
$D_{\unicode[STIX]{x1D707}^{1}}\otimes D_{\unicode[STIX]{x1D707}^{2}}$
,
![]() $\unicode[STIX]{x1D707}^{1}\in {\mathcal{P}}_{2}(m)$
,
$\unicode[STIX]{x1D707}^{1}\in {\mathcal{P}}_{2}(m)$
,
![]() $\unicode[STIX]{x1D707}^{2}\in {\mathcal{P}}_{2}(N-m)$
. In particular, the stable part
$\unicode[STIX]{x1D707}^{2}\in {\mathcal{P}}_{2}(N-m)$
. In particular, the stable part
![]() $\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\operatorname{st}}$
is generated by irreducible representations of the Hecke algebra of
$\operatorname{H}^{\ast }(\operatorname{Hess},\mathbb{C})_{\operatorname{st}}$
is generated by irreducible representations of the Hecke algebra of
![]() $S_{N}$
at
$S_{N}$
at
![]() $q=-1$
.
$q=-1$
.
Proof. Part (1) is clear. To prove part (2) we proceed as follows. By the decomposition theorem
![]() $\unicode[STIX]{x1D70B}_{\ast }\mathbb{C}$
is a direct sum of shifts of nilpotent orbital complexes. Since
$\unicode[STIX]{x1D70B}_{\ast }\mathbb{C}$
is a direct sum of shifts of nilpotent orbital complexes. Since
![]() $\mathfrak{F}(\unicode[STIX]{x1D70B}_{\ast }\mathbb{C})\cong \check{\unicode[STIX]{x1D70B}}_{\ast }\mathbb{C}$
(up to shift), Theorem 4.1 implies that a generic stalk of
$\mathfrak{F}(\unicode[STIX]{x1D70B}_{\ast }\mathbb{C})\cong \check{\unicode[STIX]{x1D70B}}_{\ast }\mathbb{C}$
(up to shift), Theorem 4.1 implies that a generic stalk of
![]() $\check{\unicode[STIX]{x1D70B}}_{\ast }\mathbb{C}$
, which is isomorphic to
$\check{\unicode[STIX]{x1D70B}}_{\ast }\mathbb{C}$
, which is isomorphic to
![]() $H^{\ast }(\operatorname{Hess},\mathbb{C})$
, is a direct sum of the local systems
$H^{\ast }(\operatorname{Hess},\mathbb{C})$
, is a direct sum of the local systems
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}=\operatorname{Ind}_{\mathbb{C}[B_{m,N-m}]}^{\mathbb{C}[B_{N}]}D_{\unicode[STIX]{x1D707}_{1}}\otimes D_{\unicode[STIX]{x1D707}_{2}}$
introduced in (2.8). Since
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}=\operatorname{Ind}_{\mathbb{C}[B_{m,N-m}]}^{\mathbb{C}[B_{N}]}D_{\unicode[STIX]{x1D707}_{1}}\otimes D_{\unicode[STIX]{x1D707}_{2}}$
introduced in (2.8). Since
![]() $I_{N}$
acts on
$I_{N}$
acts on
![]() $V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
by the formula
$V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}}$
by the formula
![]() $a.(b\otimes v)=((b.\unicode[STIX]{x1D712}_{m})(a))(b\otimes v)$
for
$a.(b\otimes v)=((b.\unicode[STIX]{x1D712}_{m})(a))(b\otimes v)$
for
![]() $a\in I_{N}$
,
$a\in I_{N}$
,
![]() $b\in B_{N}$
and
$b\in B_{N}$
and
![]() $v\in D_{\unicode[STIX]{x1D707}_{1}}\otimes D_{\unicode[STIX]{x1D707}_{2}}$
, we have
$v\in D_{\unicode[STIX]{x1D707}_{1}}\otimes D_{\unicode[STIX]{x1D707}_{2}}$
, we have
![]() $(V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}})_{\unicode[STIX]{x1D712}}\cong D_{\unicode[STIX]{x1D707}_{1}}\otimes D_{\unicode[STIX]{x1D707}_{2}}$
. The theorem follows.◻
$(V_{\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2}})_{\unicode[STIX]{x1D712}}\cong D_{\unicode[STIX]{x1D707}_{1}}\otimes D_{\unicode[STIX]{x1D707}_{2}}$
. The theorem follows.◻
Example 5.3. Let
![]() $C$
be the hyper-elliptic curve with affine equation
$C$
be the hyper-elliptic curve with affine equation
![]() $y^{2}=\prod _{j=1}^{N}(x-a_{j})$
(here
$y^{2}=\prod _{j=1}^{N}(x-a_{j})$
(here
![]() $a_{i}\neq a_{j}$
for
$a_{i}\neq a_{j}$
for
![]() $i\neq j$
). Assume
$i\neq j$
). Assume
![]() $N=2n+2$
is even. Then according to [Reference Chen, Vilonen and XueCVX17, § 2.3] the Jacobian
$N=2n+2$
is even. Then according to [Reference Chen, Vilonen and XueCVX17, § 2.3] the Jacobian
![]() $\operatorname{Jac}(C)$
is an example of Hessenberg variety and the monodromy action of
$\operatorname{Jac}(C)$
is an example of Hessenberg variety and the monodromy action of
![]() $\unicode[STIX]{x1D70B}_{1}(\mathfrak{g}_{1}^{\text{rs}},s)$
factors through
$\unicode[STIX]{x1D70B}_{1}(\mathfrak{g}_{1}^{\text{rs}},s)$
factors through
![]() $B_{N}$
, that is,
$B_{N}$
, that is,
![]() $\operatorname{H}^{\ast }(\operatorname{Jac}(C),\mathbb{C})=\operatorname{H}^{\ast }(\operatorname{Jac}(C),\mathbb{C})_{\operatorname{st}}$
. Let
$\operatorname{H}^{\ast }(\operatorname{Jac}(C),\mathbb{C})=\operatorname{H}^{\ast }(\operatorname{Jac}(C),\mathbb{C})_{\operatorname{st}}$
. Let
![]() $\unicode[STIX]{x1D707}_{k}=(N-k,k)\in {\mathcal{P}}_{2}(N)$
and
$\unicode[STIX]{x1D707}_{k}=(N-k,k)\in {\mathcal{P}}_{2}(N)$
and
![]() $D_{\unicode[STIX]{x1D707}_{k}}$
be the corresponding representation of
$D_{\unicode[STIX]{x1D707}_{k}}$
be the corresponding representation of
![]() ${\mathcal{H}}_{N,-1}$
. Using [Reference A’CampoA’Ca79], one can check that the induced action of the group algebra
${\mathcal{H}}_{N,-1}$
. Using [Reference A’CampoA’Ca79], one can check that the induced action of the group algebra
![]() $\mathbb{C}[B_{N}]$
on
$\mathbb{C}[B_{N}]$
on
![]() $\operatorname{H}^{i}(\operatorname{Jac}(C),\mathbb{C})$
factors through
$\operatorname{H}^{i}(\operatorname{Jac}(C),\mathbb{C})$
factors through
![]() ${\mathcal{H}}_{N,-1}$
and for
${\mathcal{H}}_{N,-1}$
and for
![]() $i\leqslant n$
the resulting representation of
$i\leqslant n$
the resulting representation of
![]() ${\mathcal{H}}_{N,-1}$
is isomorphic to
${\mathcal{H}}_{N,-1}$
is isomorphic to
 $$\begin{eqnarray}\operatorname{H}^{i}(\operatorname{Jac}(C),\mathbb{C})\cong \bigoplus _{j=0}^{[i/2]}D_{\unicode[STIX]{x1D707}_{i-2j}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{H}^{i}(\operatorname{Jac}(C),\mathbb{C})\cong \bigoplus _{j=0}^{[i/2]}D_{\unicode[STIX]{x1D707}_{i-2j}}\end{eqnarray}$$
with the primitive part
![]() $\operatorname{H}^{i}(\operatorname{Jac}(C),\mathbb{C})_{\text{prim}}\cong D_{\unicode[STIX]{x1D707}_{i}}$
.
$\operatorname{H}^{i}(\operatorname{Jac}(C),\mathbb{C})_{\text{prim}}\cong D_{\unicode[STIX]{x1D707}_{i}}$
.
Remark 5.4. It would be nice to have an explicit decomposition of
![]() $H^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{m}}$
into irreducible representations of
$H^{\ast }(\operatorname{Hess},\mathbb{C})_{\unicode[STIX]{x1D712}_{m}}$
into irreducible representations of
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
. For this one needs finer information for the bijection in Theorem 4.1 (see § 7). In [Reference Chen, Vilonen and XueCVX15a, Reference Chen, Vilonen and XueCVX17], we establish an explicit bijection for certain nilpotent orbital complexes and we work out an explicit decomposition for the cohomology of the Hessenberg varieties that are isomorphic to Fano varieties of
${\mathcal{H}}_{\unicode[STIX]{x1D712}_{m},-1}$
. For this one needs finer information for the bijection in Theorem 4.1 (see § 7). In [Reference Chen, Vilonen and XueCVX15a, Reference Chen, Vilonen and XueCVX17], we establish an explicit bijection for certain nilpotent orbital complexes and we work out an explicit decomposition for the cohomology of the Hessenberg varieties that are isomorphic to Fano varieties of
![]() $k$
-planes in smooth complete intersections of two quadrics in projective space.
$k$
-planes in smooth complete intersections of two quadrics in projective space.
6 Representations of
 ${\mathcal{H}}_{N,-1}$
${\mathcal{H}}_{N,-1}$
In this section we show that all irreducible representations of the Hecke algebra
![]() ${\mathcal{H}}_{N,-1}$
come from geometry. Indeed they all appear in intersection cohomology of a Hessenberg variety with coefficient in a local system. In particular, this shows that all irreducible representations of
${\mathcal{H}}_{N,-1}$
come from geometry. Indeed they all appear in intersection cohomology of a Hessenberg variety with coefficient in a local system. In particular, this shows that all irreducible representations of
![]() ${\mathcal{H}}_{N,-1}$
carry a Hodge structure. In particular, the irreducible representations of
${\mathcal{H}}_{N,-1}$
carry a Hodge structure. In particular, the irreducible representations of
![]() ${\mathcal{H}}_{N,-1}$
can be viewed as variations of Hodge structure.
${\mathcal{H}}_{N,-1}$
can be viewed as variations of Hodge structure.
Let
![]() ${\mathcal{O}}$
be a nilpotent
${\mathcal{O}}$
be a nilpotent
![]() $K$
-orbit on
$K$
-orbit on
![]() $\mathfrak{g}_{1}$
and
$\mathfrak{g}_{1}$
and
![]() ${\mathcal{L}}$
an irreducible
${\mathcal{L}}$
an irreducible
![]() $K$
-equivariant local system on
$K$
-equivariant local system on
![]() ${\mathcal{O}}$
. We call
${\mathcal{O}}$
. We call
![]() $({\mathcal{O}},{\mathcal{L}})$
a nilpotent pair. Following [Reference Lusztig and YunLY17], we associate to each nilpotent pair
$({\mathcal{O}},{\mathcal{L}})$
a nilpotent pair. Following [Reference Lusztig and YunLY17], we associate to each nilpotent pair
![]() $({\mathcal{O}},{\mathcal{L}})$
two families of Hessenberg varieties
$({\mathcal{O}},{\mathcal{L}})$
two families of Hessenberg varieties
![]() $\operatorname{Hess}_{{\mathcal{L}},\pm 1}\rightarrow \mathfrak{g}_{1}$
together with local systems
$\operatorname{Hess}_{{\mathcal{L}},\pm 1}\rightarrow \mathfrak{g}_{1}$
together with local systems
![]() $\hat{{\mathcal{L}}}_{\pm 1}$
on open subsets
$\hat{{\mathcal{L}}}_{\pm 1}$
on open subsets
![]() $\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1}\subset \operatorname{Hess}_{{\mathcal{L}},\pm 1}$
.
$\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1}\subset \operatorname{Hess}_{{\mathcal{L}},\pm 1}$
.
Let
![]() $x\in \mathfrak{g}_{1}$
be a nilpotent element in
$x\in \mathfrak{g}_{1}$
be a nilpotent element in
![]() ${\mathcal{O}}$
. Choose a normal
${\mathcal{O}}$
. Choose a normal
![]() $\operatorname{sl}_{2}$
-triple
$\operatorname{sl}_{2}$
-triple
![]() $\{x,h,y\}$
and let
$\{x,h,y\}$
and let
For any
![]() $N\in \mathbb{Z}$
we write
$N\in \mathbb{Z}$
we write
![]() $\text{}\underline{N}\in \{0,1\}$
for its image in
$\text{}\underline{N}\in \{0,1\}$
for its image in
![]() $\mathbb{Z}/2\mathbb{Z}$
. Define
$\mathbb{Z}/2\mathbb{Z}$
. Define
One can check that
![]() $\mathfrak{l}^{x}\subset \mathfrak{g}$
is a graded Lie subalgebra of
$\mathfrak{l}^{x}\subset \mathfrak{g}$
is a graded Lie subalgebra of
![]() $\mathfrak{g}$
and
$\mathfrak{g}$
and
![]() $x\in \mathfrak{l}_{1}^{x}=\mathfrak{g}_{1}(2)$
. Let
$x\in \mathfrak{l}_{1}^{x}=\mathfrak{g}_{1}(2)$
. Let
![]() $L_{0}^{x}\subset K$
be the reductive subgroup with Lie algebra
$L_{0}^{x}\subset K$
be the reductive subgroup with Lie algebra
![]() $\mathfrak{l}_{0}^{x}=\mathfrak{g}_{0}(0)$
. By [Reference Lusztig and YunLY17, 2.9(c)], the restriction
$\mathfrak{l}_{0}^{x}=\mathfrak{g}_{0}(0)$
. By [Reference Lusztig and YunLY17, 2.9(c)], the restriction
is an irreducible
![]() $L_{0}^{x}$
-equivariant local system on the unique open
$L_{0}^{x}$
-equivariant local system on the unique open
![]() $L_{0}^{x}$
-orbit
$L_{0}^{x}$
-orbit
![]() $\stackrel{\circ }{\mathfrak{l}_{1}^{x}}$
on
$\stackrel{\circ }{\mathfrak{l}_{1}^{x}}$
on
![]() $\mathfrak{l}_{1}^{x}$
.
$\mathfrak{l}_{1}^{x}$
.
According to [Reference LusztigLus95], there exists a graded parabolic subalgebra
![]() $\mathfrak{q}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{q}_{N}$
of
$\mathfrak{q}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{q}_{N}$
of
![]() $\mathfrak{l}^{x}$
, a Levi subalgebra
$\mathfrak{l}^{x}$
, a Levi subalgebra
![]() $\mathfrak{m}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{m}_{N}$
of
$\mathfrak{m}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{m}_{N}$
of
![]() $\mathfrak{q}$
, and a cuspidal local system
$\mathfrak{q}$
, and a cuspidal local system
![]() ${\mathcal{L}}_{1}$
on the open
${\mathcal{L}}_{1}$
on the open
![]() $M_{0}$
-orbit
$M_{0}$
-orbit
![]() $\stackrel{\circ }{\mathfrak{m}}_{1}$
of
$\stackrel{\circ }{\mathfrak{m}}_{1}$
of
![]() $\mathfrak{m}_{1}$
(here
$\mathfrak{m}_{1}$
(here
![]() $M_{0}$
is the reductive subgroup of
$M_{0}$
is the reductive subgroup of
![]() $L_{0}^{x}$
with Lie algebra
$L_{0}^{x}$
with Lie algebra
![]() $\mathfrak{m}_{0}$
) such that
$\mathfrak{m}_{0}$
) such that
In addition, we have
where
![]() ${\mathcal{L}}_{-1}$
is a cuspidal local system on the unique open orbit
${\mathcal{L}}_{-1}$
is a cuspidal local system on the unique open orbit
![]() $\stackrel{\circ }{\mathfrak{m}}_{-1}\subset \mathfrak{m}_{-1}$
.
$\stackrel{\circ }{\mathfrak{m}}_{-1}\subset \mathfrak{m}_{-1}$
.
Define
![]() $\hat{\mathfrak{q}}_{N}$
to be the pre-image of
$\hat{\mathfrak{q}}_{N}$
to be the pre-image of
![]() $\mathfrak{q}_{N}$
under the projection map
$\mathfrak{q}_{N}$
under the projection map
![]() $\mathfrak{p}_{N}^{x}\rightarrow \mathfrak{l}_{N}^{x}$
. Let
$\mathfrak{p}_{N}^{x}\rightarrow \mathfrak{l}_{N}^{x}$
. Let
![]() $Q_{K}\subset K$
be the parabolic subgroup with Lie algebra
$Q_{K}\subset K$
be the parabolic subgroup with Lie algebra
![]() $\hat{\mathfrak{q}}_{0}$
. Denote by
$\hat{\mathfrak{q}}_{0}$
. Denote by
![]() $\stackrel{\circ }{\hat{\mathfrak{q}}}_{\pm 1}$
the preimage of
$\stackrel{\circ }{\hat{\mathfrak{q}}}_{\pm 1}$
the preimage of
![]() $\stackrel{\circ }{\mathfrak{m}}_{\pm 1}$
under the projection map
$\stackrel{\circ }{\mathfrak{m}}_{\pm 1}$
under the projection map
![]() $\hat{\mathfrak{q}}_{\pm 1}\rightarrow \mathfrak{q}_{\pm 1}\rightarrow \mathfrak{m}_{\pm 1}$
. The group
$\hat{\mathfrak{q}}_{\pm 1}\rightarrow \mathfrak{q}_{\pm 1}\rightarrow \mathfrak{m}_{\pm 1}$
. The group
![]() $Q_{K}$
acts naturally on
$Q_{K}$
acts naturally on
![]() $\hat{\mathfrak{q}}_{\pm 1}$
and
$\hat{\mathfrak{q}}_{\pm 1}$
and
![]() $\stackrel{\circ }{\hat{\mathfrak{q}}}_{\pm 1}$
and we define
$\stackrel{\circ }{\hat{\mathfrak{q}}}_{\pm 1}$
and we define
Let
and let
![]() $\stackrel{\circ }{\unicode[STIX]{x1D70B}}_{{\mathcal{L}},\pm 1}$
be its restriction to
$\stackrel{\circ }{\unicode[STIX]{x1D70B}}_{{\mathcal{L}},\pm 1}$
be its restriction to
![]() $\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1}$
. For any
$\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1}$
. For any
![]() $s\in \mathfrak{g}_{1}$
, we denote by
$s\in \mathfrak{g}_{1}$
, we denote by
![]() $\operatorname{Hess}_{{\mathcal{L}},\pm 1,s}$
and
$\operatorname{Hess}_{{\mathcal{L}},\pm 1,s}$
and
![]() $\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1,s}$
the fiber of
$\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1,s}$
the fiber of
![]() $\unicode[STIX]{x1D70B}_{{\mathcal{L}},\pm 1}$
and
$\unicode[STIX]{x1D70B}_{{\mathcal{L}},\pm 1}$
and
![]() $\stackrel{\circ }{\unicode[STIX]{x1D70B}}_{{\mathcal{L}},\pm 1}$
over
$\stackrel{\circ }{\unicode[STIX]{x1D70B}}_{{\mathcal{L}},\pm 1}$
over
![]() $s$
, respectively.
$s$
, respectively.
There are natural maps
sending
![]() $(k,v)\in \operatorname{Hess}_{{\mathcal{L}},\pm 1}=K\times ^{Q_{K}}\hat{\mathfrak{q}}_{\pm 1}$
to
$(k,v)\in \operatorname{Hess}_{{\mathcal{L}},\pm 1}=K\times ^{Q_{K}}\hat{\mathfrak{q}}_{\pm 1}$
to
![]() $\bar{v}$
, the image of
$\bar{v}$
, the image of
![]() $v\in \hat{\mathfrak{q}}_{\pm 1}$
under the map
$v\in \hat{\mathfrak{q}}_{\pm 1}$
under the map
![]() $\hat{\mathfrak{q}}_{\pm 1}\rightarrow \mathfrak{m}_{\pm 1}\rightarrow [\mathfrak{m}_{\pm 1}/M_{0}]$
. We define the following local system
$\hat{\mathfrak{q}}_{\pm 1}\rightarrow \mathfrak{m}_{\pm 1}\rightarrow [\mathfrak{m}_{\pm 1}/M_{0}]$
. We define the following local system
on
![]() $\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1}$
. Here we view the
$\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}},\pm 1}$
. Here we view the
![]() $M_{0}$
-local systems
$M_{0}$
-local systems
![]() ${\mathcal{L}}_{\pm 1}$
as sheaves on
${\mathcal{L}}_{\pm 1}$
as sheaves on
![]() $[\stackrel{\circ }{\mathfrak{m}}_{\pm 1}/M_{0}]$
.
$[\stackrel{\circ }{\mathfrak{m}}_{\pm 1}/M_{0}]$
.
Example 6.1. Consider the nilpotent pair
![]() $({\mathcal{O}},{\mathcal{L}}={\mathcal{L}}_{\operatorname{triv}})$
where
$({\mathcal{O}},{\mathcal{L}}={\mathcal{L}}_{\operatorname{triv}})$
where
![]() ${\mathcal{L}}_{\operatorname{triv}}$
is the trivial local system on
${\mathcal{L}}_{\operatorname{triv}}$
is the trivial local system on
![]() ${\mathcal{O}}$
. Using [Reference LusztigLus95, Proposition 7.3] one can check that in this case
${\mathcal{O}}$
. Using [Reference LusztigLus95, Proposition 7.3] one can check that in this case
![]() $\mathfrak{q}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{q}_{N}$
is a Borel subalgebra of
$\mathfrak{q}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{q}_{N}$
is a Borel subalgebra of
![]() $\mathfrak{l}^{x}$
and
$\mathfrak{l}^{x}$
and
![]() $\mathfrak{m}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{m}_{N}$
is a Cartan subalgebra. Moreover the grading on
$\mathfrak{m}=\bigoplus _{N\in \mathbb{Z}}\mathfrak{m}_{N}$
is a Cartan subalgebra. Moreover the grading on
![]() $\mathfrak{m}$
is concentrated in degree zero, i.e.,
$\mathfrak{m}$
is concentrated in degree zero, i.e.,
![]() $\mathfrak{m}=\mathfrak{m}_{0}$
, and the cuspidal local system
$\mathfrak{m}=\mathfrak{m}_{0}$
, and the cuspidal local system
![]() ${\mathcal{L}}_{\pm 1}$
is the skyscraper sheaf supported on
${\mathcal{L}}_{\pm 1}$
is the skyscraper sheaf supported on
![]() $\mathfrak{m}_{\pm 1}=\{0\}$
. It follows that in this case
$\mathfrak{m}_{\pm 1}=\{0\}$
. It follows that in this case
![]() $\operatorname{Hess}_{{\mathcal{L}}_{\operatorname{triv}},\pm 1}=\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}}_{\operatorname{triv}},\pm 1}$
and
$\operatorname{Hess}_{{\mathcal{L}}_{\operatorname{triv}},\pm 1}=\stackrel{\circ }{\operatorname{Hess}}_{{\mathcal{L}}_{\operatorname{triv}},\pm 1}$
and
![]() $\hat{{\mathcal{L}}}_{\pm 1}$
is the constant local system.
$\hat{{\mathcal{L}}}_{\pm 1}$
is the constant local system.
In [Reference Lusztig and YunLY17, § 7], the authors prove the following:
Assume from now on that
![]() $\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1}\,:\,\operatorname{Hess}_{{\mathcal{L}},-1}\rightarrow \mathfrak{g}_{1}$
is surjective. Then the sheaf
$\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1}\,:\,\operatorname{Hess}_{{\mathcal{L}},-1}\rightarrow \mathfrak{g}_{1}$
is surjective. Then the sheaf
![]() $(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
is smooth over
$(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
is smooth over
![]() $\mathfrak{g}_{1}^{\text{rs}}$
. One sees this as follows. According to the first statement of (6.1) the characteristic variety of
$\mathfrak{g}_{1}^{\text{rs}}$
. One sees this as follows. According to the first statement of (6.1) the characteristic variety of
![]() $(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
coincides with that of
$(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
coincides with that of
![]() $(\unicode[STIX]{x1D70B}_{{\mathcal{L}},1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},1},\hat{{\mathcal{L}}}_{1})$
as they are Fourier transforms of each other. But
$(\unicode[STIX]{x1D70B}_{{\mathcal{L}},1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},1},\hat{{\mathcal{L}}}_{1})$
as they are Fourier transforms of each other. But
![]() $(\unicode[STIX]{x1D70B}_{{\mathcal{L}},1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},1},\hat{{\mathcal{L}}}_{1})$
is
$(\unicode[STIX]{x1D70B}_{{\mathcal{L}},1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},1},\hat{{\mathcal{L}}}_{1})$
is
![]() $K$
-equivariant and supported on the nilpotent cone. A straightforward calculation then shows the smoothness of
$K$
-equivariant and supported on the nilpotent cone. A straightforward calculation then shows the smoothness of
![]() $(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
on
$(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
on
![]() $\mathfrak{g}_{1}^{\text{rs}}$
. Thus, by the decomposition theorem, we conclude that
$\mathfrak{g}_{1}^{\text{rs}}$
. Thus, by the decomposition theorem, we conclude that
In addition, the
![]() $\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
and hence
$\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
and hence
![]() $(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
has a canonical structure as a Hodge module and thus the direct summands are
$(\unicode[STIX]{x1D70B}_{{\mathcal{L}},-1})_{\ast }\operatorname{IC}(\operatorname{Hess}_{{\mathcal{L}},-1},\hat{{\mathcal{L}}}_{-1})$
has a canonical structure as a Hodge module and thus the direct summands are
![]() $\operatorname{IC}$
-extensions of irreducible variations of pure Hodge structure, see, [Reference SaitoSai88].
$\operatorname{IC}$
-extensions of irreducible variations of pure Hodge structure, see, [Reference SaitoSai88].
We fix a generic
![]() $s\in \mathfrak{g}_{1}^{\text{rs}}$
and then
$s\in \mathfrak{g}_{1}^{\text{rs}}$
and then
Thus we obtain an action of the fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)$
on
$\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)$
on
![]() $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})$
and by the discussion above this action breaks into a direct sum of irreducible representations which are also variations of Hodge structure.
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})$
and by the discussion above this action breaks into a direct sum of irreducible representations which are also variations of Hodge structure.
The component group
![]() $\unicode[STIX]{x1D70B}_{0}(Z_{K}(s))\cong I_{N}$
acts on
$\unicode[STIX]{x1D70B}_{0}(Z_{K}(s))\cong I_{N}$
acts on
![]() $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})$
and we write
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})$
and we write
for the corresponding eigenspace decomposition.
Definition 6.2. The stable part
![]() $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})_{\operatorname{st}}$
of
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})_{\operatorname{st}}$
of
![]() $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})$
is the direct summand
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})$
is the direct summand
![]() $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})_{\unicode[STIX]{x1D712}_{\operatorname{triv}}}$
where
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})_{\unicode[STIX]{x1D712}_{\operatorname{triv}}}$
where
![]() $\unicode[STIX]{x1D712}_{\operatorname{triv}}\in I_{N}^{\vee }$
is the trivial character.
$\unicode[STIX]{x1D712}_{\operatorname{triv}}\in I_{N}^{\vee }$
is the trivial character.
Observe that
![]() $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})_{\operatorname{st}}$
is stable under the monodromy action of
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}},-1,s},\hat{{\mathcal{L}}}_{-1})_{\operatorname{st}}$
is stable under the monodromy action of
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)$
. Moreover, the action factors through the braid group
$\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)$
. Moreover, the action factors through the braid group
![]() $B_{N}$
via the quotient map
$B_{N}$
via the quotient map
![]() $\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)\rightarrow B_{N}$
.
$\unicode[STIX]{x1D70B}_{1}^{K}(\mathfrak{g}_{1}^{\text{rs}},s)\rightarrow B_{N}$
.
For every irreducible representation
![]() $D_{\unicode[STIX]{x1D707}}$
of
$D_{\unicode[STIX]{x1D707}}$
of
![]() ${\mathcal{H}}_{N,-1}$
, let
${\mathcal{H}}_{N,-1}$
, let
![]() $V_{\unicode[STIX]{x1D707}}$
be the local system on
$V_{\unicode[STIX]{x1D707}}$
be the local system on
![]() $\mathfrak{g}_{1}^{\text{rs}}$
associated to
$\mathfrak{g}_{1}^{\text{rs}}$
associated to
![]() $D_{\unicode[STIX]{x1D707}}$
. By Theorem 4.1, there exists a unique nilpotent pair
$D_{\unicode[STIX]{x1D707}}$
. By Theorem 4.1, there exists a unique nilpotent pair
![]() $({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{L}}_{\unicode[STIX]{x1D707}})$
such that
$({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{L}}_{\unicode[STIX]{x1D707}})$
such that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{L}}_{\unicode[STIX]{x1D707}}))\cong \operatorname{IC}(\mathfrak{g}_{1},V_{\unicode[STIX]{x1D707}})$
.
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{L}}_{\unicode[STIX]{x1D707}}))\cong \operatorname{IC}(\mathfrak{g}_{1},V_{\unicode[STIX]{x1D707}})$
.
Theorem 6.3. Let
![]() $D_{\unicode[STIX]{x1D707}}$
be an irreducible representation of
$D_{\unicode[STIX]{x1D707}}$
be an irreducible representation of
![]() ${\mathcal{H}}_{N,-1}$
and let
${\mathcal{H}}_{N,-1}$
and let
![]() $({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{L}}_{\unicode[STIX]{x1D707}})$
be the associated nilpotent pair as above. We have the following.
$({\mathcal{O}}_{\unicode[STIX]{x1D707}},{\mathcal{L}}_{\unicode[STIX]{x1D707}})$
be the associated nilpotent pair as above. We have the following.
(i) The map
 $\unicode[STIX]{x1D70B}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1}$
is onto, the action of the braid group
$\unicode[STIX]{x1D70B}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1}$
is onto, the action of the braid group
 $B_{N}$
on
$B_{N}$
on
 $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
factors through the Hecke algebra
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
factors through the Hecke algebra
 ${\mathcal{H}}_{N,-1}$
and
${\mathcal{H}}_{N,-1}$
and
 $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
is a direct sum of irreducible representations of
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
is a direct sum of irreducible representations of
 ${\mathcal{H}}_{N,-1}$
.
${\mathcal{H}}_{N,-1}$
.(ii)
 $D_{\unicode[STIX]{x1D707}}$
appears in
$D_{\unicode[STIX]{x1D707}}$
appears in
 $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
with non-zero multiplicity.
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
with non-zero multiplicity.
Proof. Since for every irreducible subrepresentation
![]() $W$
of
$W$
of
![]() $\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
the corresponding Fourier transform
$\operatorname{IH\ast}(\operatorname{Hess}_{{\mathcal{L}}_{\unicode[STIX]{x1D707}},-1,s},\hat{{\mathcal{L}}}_{\unicode[STIX]{x1D707},-1})_{\operatorname{st}}$
the corresponding Fourier transform
![]() $\mathfrak{F}(\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{W}}))$
is supported on the nilpotent cone (here
$\mathfrak{F}(\operatorname{IC}(\mathfrak{g}_{1},{\mathcal{W}}))$
is supported on the nilpotent cone (here
![]() ${\mathcal{W}}$
is the local system on
${\mathcal{W}}$
is the local system on
![]() $\mathfrak{g}_{1}^{\text{rs}}$
associated to
$\mathfrak{g}_{1}^{\text{rs}}$
associated to
![]() $W$
), the same argument as in the proof of Theorem 5.2 implies part (1). Part (2) follows from (6.1), (6.2), and (6.4).◻
$W$
), the same argument as in the proof of Theorem 5.2 implies part (1). Part (2) follows from (6.1), (6.2), and (6.4).◻
7 Conjecture on more precise matching
In Theorem 4.1 we show that the Fourier transform establishes a bijection between two sets of intersection cohomology sheaves. In this section we formulate a conjecture which refines the bijection in Theorem 4.1. We also relate the conjecture to our earlier conjectures in [Reference Chen, Vilonen and XueCVX15b]. Our conjecture is not strong enough to produce an exact matching. The exact description of the bijection is crucial for applications, for example, computing cohomologies of Hessenberg varieties as explained in § 5.
We begin with associating to each nilpotent orbit
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
,
![]() $\unicode[STIX]{x1D714}=\text{I},\text{II}$
) a subset
$\unicode[STIX]{x1D714}=\text{I},\text{II}$
) a subset
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}\subset \unicode[STIX]{x1D6F4}_{N}$
(respectively
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}\subset \unicode[STIX]{x1D6F4}_{N}$
(respectively
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}\subset \unicode[STIX]{x1D6F4}_{N}$
), if
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}\subset \unicode[STIX]{x1D6F4}_{N}$
), if
![]() $\unicode[STIX]{x1D706}\in {\mathcal{P}}(N)$
has at least one odd part (respectively has only even parts). Let
$\unicode[STIX]{x1D706}\in {\mathcal{P}}(N)$
has at least one odd part (respectively has only even parts). Let
![]() $\unicode[STIX]{x1D706}$
be a partition of
$\unicode[STIX]{x1D706}$
be a partition of
![]() $N$
and let
$N$
and let
![]() $\unicode[STIX]{x1D706}^{\prime }$
be the transpose partition of
$\unicode[STIX]{x1D706}^{\prime }$
be the transpose partition of
![]() $\unicode[STIX]{x1D706}$
. Suppose that
$\unicode[STIX]{x1D706}$
. Suppose that
where
![]() $m_{i}\geqslant 1$
,
$m_{i}\geqslant 1$
,
![]() $i=1,\ldots ,k$
. Here and in what follows we write the parts in a partition in the order which is most convenient for us. In particular, in (7.1) we place the parts with even multiplicity before the parts with odd multiplicity.
$i=1,\ldots ,k$
. Here and in what follows we write the parts in a partition in the order which is most convenient for us. In particular, in (7.1) we place the parts with even multiplicity before the parts with odd multiplicity.
Let
![]() $\unicode[STIX]{x1D6FF}_{i}\in \{0,1\}$
for
$\unicode[STIX]{x1D6FF}_{i}\in \{0,1\}$
for
![]() $i\in [1,l]$
and let
$i\in [1,l]$
and let
Note that
![]() $2|\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})|+|\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})|=N$
. Let
$2|\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})|+|\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})|=N$
. Let
We define
Note that
![]() $\unicode[STIX]{x1D706}_{l+1}^{\prime }=0$
if and only if all parts of
$\unicode[STIX]{x1D706}_{l+1}^{\prime }=0$
if and only if all parts of
![]() $\unicode[STIX]{x1D706}$
are even. In this case,
$\unicode[STIX]{x1D706}$
are even. In this case,
![]() $J_{0}=\emptyset =J$
and
$J_{0}=\emptyset =J$
and
![]() $\unicode[STIX]{x1D707}^{1}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J)=\unicode[STIX]{x1D707}^{2}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J)$
and we write
$\unicode[STIX]{x1D707}^{1}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J)=\unicode[STIX]{x1D707}^{2}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J)$
and we write
![]() $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})=\unicode[STIX]{x1D707}^{i}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J)$
,
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})=\unicode[STIX]{x1D707}^{i}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J)$
,
![]() $i=1,2$
.
$i=1,2$
.
If
![]() $\unicode[STIX]{x1D706}$
has at least one odd part, then let
$\unicode[STIX]{x1D706}$
has at least one odd part, then let
 $$\begin{eqnarray}\begin{array}{@{}rl@{}}\displaystyle \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}:=\bigg\{(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l});\unicode[STIX]{x1D707}^{1}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J),\, & \unicode[STIX]{x1D707}^{2}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J))\mid \unicode[STIX]{x1D6FF}_{i}\in \{0,1\},i=1,\ldots ,l,\\ \, & \displaystyle J\subset \{l+1,\ldots ,k\},\text{ such that }\mathop{\sum }_{j\in J}\unicode[STIX]{x1D706}_{j}^{\prime }<\mathop{\sum }_{j\in J_{0}-J}\unicode[STIX]{x1D706}_{j}^{\prime }\bigg\}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rl@{}}\displaystyle \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}:=\bigg\{(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l});\unicode[STIX]{x1D707}^{1}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J),\, & \unicode[STIX]{x1D707}^{2}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l};J))\mid \unicode[STIX]{x1D6FF}_{i}\in \{0,1\},i=1,\ldots ,l,\\ \, & \displaystyle J\subset \{l+1,\ldots ,k\},\text{ such that }\mathop{\sum }_{j\in J}\unicode[STIX]{x1D706}_{j}^{\prime }<\mathop{\sum }_{j\in J_{0}-J}\unicode[STIX]{x1D706}_{j}^{\prime }\bigg\}.\end{array}\end{eqnarray}$$
If all parts of
![]() $\unicode[STIX]{x1D706}$
are even (in which case
$\unicode[STIX]{x1D706}$
are even (in which case
![]() $\unicode[STIX]{x1D706}_{l+1}^{\prime }=0$
), then let
$\unicode[STIX]{x1D706}_{l+1}^{\prime }=0$
), then let
We have
![]() $|\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}|=2^{k-1}$
(respectively
$|\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}|=2^{k-1}$
(respectively
![]() $|\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}|=2^{l}$
), which equals the number of non-isomorphic irreducible
$|\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}|=2^{l}$
), which equals the number of non-isomorphic irreducible
![]() $K$
-equvariant local systems on
$K$
-equvariant local systems on
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
${\mathcal{O}}_{\unicode[STIX]{x1D706}}$
(respectively
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
).
${\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}$
).
Conjecture 7.1. Let
![]() $\unicode[STIX]{x1D706}$
be a partition of
$\unicode[STIX]{x1D706}$
be a partition of
![]() $N$
.
$N$
.
(1) If
![]() $\unicode[STIX]{x1D706}$
has at least one odd part, then the Fourier transform
$\unicode[STIX]{x1D706}$
has at least one odd part, then the Fourier transform
![]() $\mathfrak{F}$
induces the following bijection:
$\mathfrak{F}$
induces the following bijection:
Moreover,
where
![]() $(\unicode[STIX]{x1D708}_{0};\unicode[STIX]{x1D707}_{0}^{1},\unicode[STIX]{x1D707}_{0}^{2})\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}$
is the unique triple such that
$(\unicode[STIX]{x1D708}_{0};\unicode[STIX]{x1D707}_{0}^{1},\unicode[STIX]{x1D707}_{0}^{2})\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}$
is the unique triple such that
![]() $|\unicode[STIX]{x1D708}_{0}|=\max \{|\unicode[STIX]{x1D708}|,(\unicode[STIX]{x1D708},\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}\}$
and the parts of
$|\unicode[STIX]{x1D708}_{0}|=\max \{|\unicode[STIX]{x1D708}|,(\unicode[STIX]{x1D708},\unicode[STIX]{x1D707}^{1},\unicode[STIX]{x1D707}^{2})\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}\}$
and the parts of
![]() $\unicode[STIX]{x1D707}_{0}^{1}$
and the parts of
$\unicode[STIX]{x1D707}_{0}^{1}$
and the parts of
![]() $\unicode[STIX]{x1D707}_{0}^{2}$
have the opposite parity (in particular, all parts of
$\unicode[STIX]{x1D707}_{0}^{2}$
have the opposite parity (in particular, all parts of
![]() $\unicode[STIX]{x1D707}_{0}^{i}$
have the same parity).
$\unicode[STIX]{x1D707}_{0}^{i}$
have the same parity).
(2) If all parts of
![]() $\unicode[STIX]{x1D706}$
are even, then the Fourier transform induces the following bijection
$\unicode[STIX]{x1D706}$
are even, then the Fourier transform induces the following bijection
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \mathfrak{F}:\{\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},{\mathcal{E}})\,|\,\unicode[STIX]{x1D714}=\text{I},\text{II},~{\mathcal{E}}\text{ irreducible }K\text{-}\text{equivariant local system on }{\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}(\text{up to isom})\}\\ \xrightarrow[{}]{{\sim}}\{\operatorname{IC}(\mathfrak{g}_{1}^{|\unicode[STIX]{x1D708}|},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})\mid \unicode[STIX]{x1D714}=\text{I},\text{II},~(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},~\unicode[STIX]{x1D707}\neq \emptyset \}\\ \cup \,\big\{\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset ))\mid \unicode[STIX]{x1D714}=\text{I},\text{II},~(\unicode[STIX]{x1D708};\emptyset ,\emptyset )\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}\big\}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle \mathfrak{F}:\{\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},{\mathcal{E}})\,|\,\unicode[STIX]{x1D714}=\text{I},\text{II},~{\mathcal{E}}\text{ irreducible }K\text{-}\text{equivariant local system on }{\mathcal{O}}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}(\text{up to isom})\}\\ \xrightarrow[{}]{{\sim}}\{\operatorname{IC}(\mathfrak{g}_{1}^{|\unicode[STIX]{x1D708}|},{\mathcal{T}}(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}})\mid \unicode[STIX]{x1D714}=\text{I},\text{II},~(\unicode[STIX]{x1D708};\unicode[STIX]{x1D707},\unicode[STIX]{x1D707})^{\unicode[STIX]{x1D714}}\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}},~\unicode[STIX]{x1D707}\neq \emptyset \}\\ \cup \,\big\{\operatorname{IC}(\mathfrak{g}_{1}^{n,\unicode[STIX]{x1D714}},{\mathcal{T}}(\unicode[STIX]{x1D708};\emptyset ,\emptyset ))\mid \unicode[STIX]{x1D714}=\text{I},\text{II},~(\unicode[STIX]{x1D708};\emptyset ,\emptyset )\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}^{\unicode[STIX]{x1D714}}\big\}.\end{array}\end{eqnarray}$$
Moreover,
where
![]() $|\unicode[STIX]{x1D708}_{0}|=n$
and
$|\unicode[STIX]{x1D708}_{0}|=n$
and
![]() $(\unicode[STIX]{x1D708}_{0};\emptyset ,\emptyset )\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}$
.
$(\unicode[STIX]{x1D708}_{0};\emptyset ,\emptyset )\in \unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D706}}$
.
Note that
![]() $\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))$
has full support if and only if
$\mathfrak{F}(\operatorname{IC}({\mathcal{O}}_{\unicode[STIX]{x1D706}},{\mathcal{E}}))$
has full support if and only if
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})=\emptyset$
. Thus we see that the conjecture is compatible with Corollary 4.9. We also remark that special cases of the conjecture are verified by [Reference Chen, Vilonen and XueCVX15a, Theorems 4.1 and 4.3].
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{l})=\emptyset$
. Thus we see that the conjecture is compatible with Corollary 4.9. We also remark that special cases of the conjecture are verified by [Reference Chen, Vilonen and XueCVX15a, Theorems 4.1 and 4.3].
Let us relate the conjecture above to our previous conjectures in [Reference Chen, Vilonen and XueCVX15b]. In [Reference Chen, Vilonen and XueCVX15b] we constructed local systems
![]() $E_{i,j}^{2n+1}$
and
$E_{i,j}^{2n+1}$
and
![]() $\widetilde{E}_{i,j}^{2n+1}$
on
$\widetilde{E}_{i,j}^{2n+1}$
on
![]() $\mathfrak{g}_{1}^{\text{rs}}$
. In terms of the parametrization introduced in this paper, we have
$\mathfrak{g}_{1}^{\text{rs}}$
. In terms of the parametrization introduced in this paper, we have
Thus we see that Conjecture 7.1 applied to
![]() $E_{i,j}^{2n+1}$
agrees with [Reference Chen, Vilonen and XueCVX15b, Conjectures 6.1 and 6.3]. Applied to
$E_{i,j}^{2n+1}$
agrees with [Reference Chen, Vilonen and XueCVX15b, Conjectures 6.1 and 6.3]. Applied to
![]() $\widetilde{E}_{i,j}^{2n+1}$
, Conjecture 7.1 implies that the supports of
$\widetilde{E}_{i,j}^{2n+1}$
, Conjecture 7.1 implies that the supports of
![]() $\mathfrak{F}(\operatorname{IC}(\mathfrak{g}_{1},\widetilde{E}_{i,j}^{2n+1}))$
are as follows:
$\mathfrak{F}(\operatorname{IC}(\mathfrak{g}_{1},\widetilde{E}_{i,j}^{2n+1}))$
are as follows:
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle {\mathcal{O}}_{3^{j}2^{2i-2j-1}1^{2n+3-4i+j}}\quad \text{if }4i-j\leqslant 2n+3,\\ {\mathcal{O}}_{3^{j}2^{2n+2-2i-j}1^{4i-j-2n-3}}\quad \text{if }2i+j\leqslant 2n+2\text{ and }4i-j\geqslant 2n+3,\\ {\mathcal{O}}_{3^{2n-2i+2}2^{2i+j-2n-2}1^{2i-2j-1}}\quad \text{if }2i+j\geqslant 2n+2.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle {\mathcal{O}}_{3^{j}2^{2i-2j-1}1^{2n+3-4i+j}}\quad \text{if }4i-j\leqslant 2n+3,\\ {\mathcal{O}}_{3^{j}2^{2n+2-2i-j}1^{4i-j-2n-3}}\quad \text{if }2i+j\leqslant 2n+2\text{ and }4i-j\geqslant 2n+3,\\ {\mathcal{O}}_{3^{2n-2i+2}2^{2i+j-2n-2}1^{2i-2j-1}}\quad \text{if }2i+j\geqslant 2n+2.\end{array}\end{eqnarray}$$
Note that the above orbits are all of even dimension and each of the even-dimensional orbits appears twice there.
Acknowledgements
We thank Misha Grinberg for helpful conversations. T.C. thanks Cheng-Chiang Tsai for useful discussions and thanks the Institute of Mathematics Academia Sinica in Taipei for support, hospitality, and a nice research environment. T.X. thanks Syu Kato for helpful discussions. Furthermore, K.V. and T.X. thank the Research Institute for Mathematical Sciences in Kyoto for support, hospitality, and a nice research environment. We also would like to thank the referee for carefully reading our manuscript and for helpful comments.