Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-19T10:28:58.161Z Has data issue: false hasContentIssue false
  • English
  • Français

SMOOTHNESS OF CONVOLUTION PRODUCTS OF ORBITAL MEASURES ON RANK ONE COMPACT SYMMETRIC SPACES

Part of: Lie groups Global differential geometry Abstract harmonic analysis

Published online by Cambridge University Press:  12 February 2016

KATHRYN E. HARE  and
JIMMY HE
KATHRYN E. HARE*
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada  N2L 3G1 email kehare@uwaterloo.ca
JIMMY HE
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, Ontario, Canada  N2L 3G1 email jimmy.he@uwaterloo.ca
*
✉kehare@uwaterloo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that all convolution products of pairs of continuous orbital measures in rank one, compact symmetric spaces are absolutely continuous and determine which convolution products are in 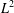$L^{2}$ (meaning that their density function is in 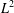$L^{2}$). We characterise the pairs whose convolution product is either absolutely continuous or in 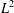$L^{2}$ in terms of the dimensions of the corresponding double cosets. In particular, we prove that if 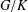$G/K$ is not 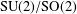$\text{SU}(2)/\text{SO}(2)$, then the convolution of any two regular orbital measures is in 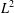$L^{2}$, while in 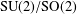$\text{SU}(2)/\text{SO}(2)$ there are no pairs of orbital measures whose convolution product is in 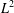$L^{2}$.

Keywords

rank one symmetric spacespherical functionsorbital measureabsolute continuity

MSC classification

Primary: 43A80: Analysis on other specific Lie groups
Secondary: 22E30: Analysis on real and complex Lie groups 53C35: Symmetric spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 1 , August 2016 , pp. 131 - 143
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Anchouche, B., Gupta, S. K. and Plagne, A., ‘Orbital measures on SU(2)/SO(2)’, Monatsh. Math. 178 (2015), 493–520.CrossRefGoogle Scholar
Bump, D., Lie Groups, Graduate Texts in Mathematics, 225 (Springer, New York, 2004).CrossRefGoogle Scholar
Cowling, M., Dooley, A., Koranyi, A. and Ricci, F., ‘An approach to symmetric spaces of rank one via groups of Heisenberg type’, J. Geom. Anal. 8 (1998), 199–237.CrossRefGoogle Scholar
Gindikin, S. and Goodman, R., ‘Restricted roots and restricted form of Weyl dimension formula for spherical varieties’, J. Lie Theory 23 (2013), 257–311.Google Scholar
Gratczyk, P. and Sawyer, P., ‘Absolute continuity of convolutions of orbital measures on Riemannian symmetric spaces’, J. Funct. Anal. 259 (2010), 1759–1770.CrossRefGoogle Scholar
Gratczyk, P. and Sawyer, P., ‘A sharp criterion for the existence of the density in the product formula on symmetric spaces of type A n ’, J. Lie Theory 20 (2010), 751–766.Google Scholar
Gupta, S. K. and Hare, K. E., ‘Convolutions of generic orbital measures in compact symmetric spaces’, Bull. Aust. Math. Soc. 79 (2009), 513–522.CrossRefGoogle Scholar
Gupta, S. K. and Hare, K. E., ‘ L 2 -singular dichotomy for orbital measures of classical compact Lie groups’, Adv. Math. 222 (2009), 1521–1573.CrossRefGoogle Scholar
Gupta, S. K. and Hare, K. E., ‘The smoothness of convolutions of zonal measures on compact symmetric spaces’, J. Math. Anal. Appl. 402 (2013), 668–678.Google Scholar
Helgason, S., Differential Geometry, Lie Groups and Symmetric Spaces (Academic Press, New York, 1978).Google Scholar
Helgason, S., Groups and Geometric Analysis: Integral Geometry, Invariant Differential Operators and Spherical Functions, Mathematical Surveys and Monographs, 83 (American Mathematical Society, Providence, RI, 2000).CrossRefGoogle Scholar
Helgason, S., Geometric Analysis of Symmetric Spaces, Mathematical Surveys and Monographs, 39 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Olver, F., Lozier, D., Boisvert, R. and Clark, C. (eds), NIST Handbook of Mathematical Functions (Cambridge University Press, New York, 2010).Google Scholar
Ragozin, D., ‘Zonal measure algebras on isotropy irreducible homogeneous spaces’, J. Funct. Anal. 17 (1974), 355–376.CrossRefGoogle Scholar
Szego, G., Orthogonal Polynomials, Colloquium Publications, 23 (American Mathematical Society, New York, 1939).Google Scholar