Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T14:00:06.397Z Has data issue: false hasContentIssue false
  • English
  • Français

A generalization of the simulation theorem for semidirect products

Published online by Cambridge University Press:  10 April 2018

SEBASTIÁN BARBIERI  and
MATHIEU SABLIK
SEBASTIÁN BARBIERI
Affiliation:
University of British Columbia, 4128-2207 Main Mall, Vancouver, British Columbia, Canada, V6T 1Z4 email sbarbieri@math.ubc.ca
MATHIEU SABLIK
Affiliation:
Institut de Mathématiques de Toulouse, UMR5219, Université de Toulouse, CNRS, Université Paul Sabatier, France email mathieu.sablik@math.univ-toulouse.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize a result of Hochman in two simultaneous directions: instead of realizing an arbitrary effectively closed 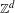$\mathbb{Z}^{d}$ action as a factor of a subaction of a 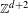$\mathbb{Z}^{d+2}$-SFT we realize an action of a finitely generated group analogously in any semidirect product of the group with 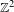$\mathbb{Z}^{2}$. Let 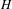$H$ be a finitely generated group and 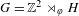$G=\mathbb{Z}^{2}\rtimes _{\unicode[STIX]{x1D711}}H$ a semidirect product. We show that for any effectively closed 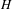$H$-dynamical system 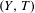$(Y,T)$ where 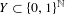$Y\subset \{0,1\}^{\mathbb{N}}$, there exists a 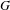$G$-subshift of finite type 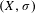$(X,\unicode[STIX]{x1D70E})$ such that the 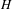$H$-subaction of 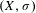$(X,\unicode[STIX]{x1D70E})$ is an extension of 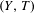$(Y,T)$. In the case where $T$ is an expansive action, a subshift conjugated to 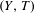$(Y,T)$ can be obtained as the 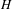$H$-projective subdynamics of a sofic 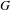$G$-subshift. As a corollary, we obtain that 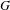$G$ admits a non-empty strongly aperiodic subshift of finite type whenever the word problem of 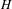$H$ is decidable.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 12 , December 2019 , pp. 3185 - 3206
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, N., Grytczuk, J., Haluszczak, M. and Riordan, O.. Nonrepetitive colorings of graphs. Random Structures Algorithms 21(3–4) (2002), 336–346.Google Scholar
Aubrun, N., Barbieri, S. and Sablik, M.. A notion of effectiveness for subshifts on finitely generated groups. Theoret. Comput. Sci. 661 (2017), 35–55.Google Scholar
Aubrun, N., Barbieri, S. and Thomassé, S.. Realization of aperiodic subshifts and uniform densities in groups. Groups, Geom. Dyn, to appear. Preprint, 2017, arXiv:1507.03369.Google Scholar
Aubrun, N. and Sablik, M.. Simulation of effective subshifts by two-dimensional subshifts of finite type. Acta Appl. Math. 126 (2013), 35–63.Google Scholar
Berger, R.. The Undecidability of the Domino Problem. American Mathematical Society, Providence, RI, 1966.Google Scholar
Boyle, M. and Lind, D.. Expansive subdynamics. Trans. Amer. Math. Soc. 349(1) (1997), 55–102.Google Scholar
Cohen, D. B.. The large scale geometry of strongly aperiodic subshifts of finite type. Adv. Math. 308 (2017), 599–626.Google Scholar
Cohen, D. B. and Goodman-Strauss, C.. Strongly aperiodic subshifts on surface groups. Groups Geom. Dyn. 11(3) (2017), 1041–1059.Google Scholar
Durand, B., Romashchenko, A. and Shen, A.. Effective closed subshifts in 1D can be implemented in 2D. Fields of Logic and Computation (Lecture Notes in Computer Scienve, 6300) . Springer, Berlin, 2010, pp. 208–226.Google Scholar
Einsiedler, M., Lind, D., Miles, R. and Ward, T.. Expansive subdynamics for algebraic ℤ d -actions. Ergod. Th. & Dynam. Sys. 21(06) (2001), 1695–1729.Google Scholar
Hanf, W.. Nonrecursive tilings of the plane. I. J. Symbolic Logic 39(2) (1974), 283–285.Google Scholar
Hochman, M.. On the dynamics and recursive properties of multidimensional symbolic systems. Invent. Math. 176(1) (2009), 131–167.Google Scholar
Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. of Math. (2) 171(3) (2010), 2011–2038.Google Scholar
Jeandel, E.. Translation-like actions and aperiodic subshifts on groups. Preprint, 2015, arXiv:1508.06419.Google Scholar
Jeandel, E. and Rao, M.. An aperiodic set of 11 Wang tiles. Preprint, 2015, arXiv:1510.02360.Google Scholar
Kari, J.. A small aperiodic set of wang tiles. Discrete Math. 160 (1996), 259–264.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Mozes, S.. Tilings, substitution systems and dynamical systems generated by them. J. Anal. Math. 53(1) (1989), 139–186.Google Scholar
Myers, D.. Nonrecursive tilings of the plane. II. J. Symbolic Logic 39(2) (1974), 286–294.Google Scholar
Robinson, R.. Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12 (1971), 177–209.Google Scholar
Şahin, A., Schraudner, M. and Ugarcovici, I.. A strongly aperiodic Heisenberg shift of finite type. Talk in Workshop on Symbolic Dynamics on Finitely Presented Groups, 2014.Google Scholar