Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-23T14:37:35.792Z Has data issue: false hasContentIssue false
  • English
  • Français

On dynamical systems preserving weights

Published online by Cambridge University Press:  03 April 2017

LAVY KOILPITCHAI  and
KUNAL MUKHERJEE
LAVY KOILPITCHAI
Affiliation:
Indian Institute of Technology Madras, Chennai 600 036, India email lavykoilpitchai@gmail.com, kunal@iitm.ac.in
KUNAL MUKHERJEE
Affiliation:
Indian Institute of Technology Madras, Chennai 600 036, India email lavykoilpitchai@gmail.com, kunal@iitm.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

The canonical unitary representation of a locally compact separable group arising from an ergodic action of the group on a von Neumann algebra with separable predual preserving a faithful normal semifinite (infinite) weight is weak mixing. On the contrary, there exists a non-ergodic automorphism of a von Neumann algebra preserving a faithful normal semifinite trace such that the spectral measure and the spectral multiplicity of the induced action are respectively the Haar measure (on the unit circle) and 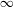$\infty$. Despite not even being ergodic, this automorphism has the same spectral data as that of a Bernoulli shift.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 7 , October 2018 , pp. 2729 - 2747
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematic Surveys and Monographs, 50) . American Mathematical Society, Providence, RI, 1997.Google Scholar
Bannon, J., Cameron, J. and Mukherjee, K.. On noncommutative joinings. Preprint, 2016.Google Scholar
Brislawn, C.. Kernels of trace class operators. Proc. Amer. Math. Soc. 104(4) (1988), 1181–1190.Google Scholar
Connes, A.. Almost periodic states and factors of type III1 . J. Funct. Anal. 16 (1974), 415–445.Google Scholar
Hajian, A.. On ergodic measure-preserving transformations defined on an infinite measure space. Proc. Amer. Math. Soc. 16(1) (1965), 45–48.Google Scholar
Hajian, A. and Kakutani, S.. Weakly wandering sets and invariant measures. Trans. Amer. Math. Soc. 110(1) (1964), 136–151.Google Scholar
Halmos, P. R.. On automorphisms of compact groups. Bull. Amer. Math. Soc. 49 (1943), 619–624.Google Scholar
Herman, R. H. and Takesaki, M.. States and automorphism groups of operator algebras. Comm. Math. Phys. 19 (1970), 142–160.Google Scholar
Høegh-Krohn, R., Landstad, M. B. and Størmer, E.. Compact ergodic groups of automorphisms. Ann. of Math. (2) 114(1) (1981), 75–86.Google Scholar
Jaks̆ić, V. and Pillet, C. A.. A note on eigenvalues of Liouvilleans. J. Statist. Phys. 105(5–6) (2001), 937–941.Google Scholar
Kaplansky, I.. Groups with representations of bounded degree. Canad. J. Math. 1 (1949), 105–112.Google Scholar
Kerr, D. and Li, Hanfeng. Ergodic Theory: Independence and Dichotomies, online book, 2014, http://www.math.tamu.edu/∼kerr/book/.Google Scholar
Kadison, R. and Ringrose, J.. Fundamentals of the Theory of Operator Algebras Vol. I: Elementary Theory. Academic Press, New York, 1983.Google Scholar
Krengel, U. and Sucheston, L.. On mixing in infinite measure space. Z. Wahrsch. verw. Geb. 13 (1969), 150–164.Google Scholar
Miles, R., Staines, M. and Ward, T.. Dynamical invariants for group automorphisms. Recent Trends in Ergodic Theory and Dynamical Systems (Contemporary Mathematics, 631) . American Mathematical Society, Providence, RI, 2015, pp. 231–258.Google Scholar
Mukherjee, K. and Patri, I.. Automorphisms of compact quantum groups. Preprint, 2016.Google Scholar
Popa, S.. Singular maximal abelian *-subalgebras in continuous von Neumann algebras. J. Funct. Anal. 50(2) (1983), 151–166.Google Scholar
Takesaki, M.. Conditional expectations in von Neumann algebras. J. Funct. Anal. 9 (1972), 306–321.Google Scholar
Takesaki, M.. Theory of Operator Algebras II (Encylopedia of Mathematical Sciences, 125) . Springer, Berlin, 2003.Google Scholar
Ştrǎtilǎ, S.. Modular Theory in Operator Algebras. Abacus Press, Tonbridge Walls, 1981, Editura Academiei, Bucharest.Google Scholar
Ştrǎtilǎ, S. and Zsidó, L.. Lectures on von Neumann Algebras. Abacus Press, Tunbridge Wells, 1979.Google Scholar