Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Runde, Volker
2011.
Completely almost periodic functionals.
Archiv der Mathematik,
Vol. 97,
Issue. 4,
p.
325.
Runde, Volker
2012.
Factorization of completely bounded maps through reflexive operator spaces with applications to weak almost periodicity.
Journal of Mathematical Analysis and Applications,
Vol. 385,
Issue. 1,
p.
477.




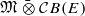 is a Banach algebra if and only if 𝔐 is subhomogeneous or
is a Banach algebra if and only if 𝔐 is subhomogeneous or 