Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-19T01:03:58.667Z Has data issue: false hasContentIssue false
  • English
  • Français

Constraints, the identifiability problem and the forecasting of mortality

Published online by Cambridge University Press:  16 March 2020

Iain D. Currie Open the ORCID record for Iain D. Currie [Opens in a new window]
Iain D. Currie*
Affiliation:
Department of Actuarial Mathematics and Statistics, and the Maxwell Institute for Mathematical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK
*
* Correspondence to: Iain D Currie, Department of Actuarial Mathematics and Statistics, and the Maxwell Institute for Mathematical Sciences, Heriot-Watt University, Edinburgh, EH14 4AS, UK. Tel: +44 (0)131 451 3203. Fax: +44 (0)131 451 3249. E-mail: I.D.Currie@hw.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Models of mortality often require constraints in order that parameters may be estimated uniquely. It is not difficult to find references in the literature to the “identifiability problem”, and papers often give arguments to justify the choice of particular constraint systems designed to deal with this problem. Many of these models are generalised linear models, and it is known that the fitted values (of mortality) in such models are identifiable, i.e., invariant with respect to the choice of constraint systems. We show that for a wide class of forecasting models, namely ARIMA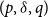 $(p,\delta, q)$ models with a fitted mean and 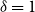$\delta = 1$ or 2, identifiability extends to the forecast values of mortality; this extended identifiability continues to hold when some model terms are smoothed. The results are illustrated with data on UK males from the Office for National Statistics for the age-period model, the age-period-cohort model, the age-period-cohort-improvements model of the Continuous Mortality Investigation and the Lee–Carter model.

Keywords

ConstraintsForecastingIdentifiabilityInvarianceMortality
Type
Paper
Information
Annals of Actuarial Science , Volume 14 , Issue 2 , September 2020 , pp. 537 - 566
Copyright
© Institute and Faculty of Actuaries 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Booth, H. & Tickle, L. (2008). Mortality modelling and forecasting: a review of methods. Annals of Actuarial Science, 3, 3–44.10.1017/S1748499500000440CrossRefGoogle Scholar
Brouhns, N., Denuit, M. & Vermunt, J.K. (2002). A Poisson log-bilinear regression approach to the construction of projected lifetables. Insurance: Mathematics and Economics, 31, 373–393.Google Scholar
Cairns, A.J.G., Blake, D. & Dowd, K. (2006). A two-factor model for stochastic mortality with parameter uncertainty: theory and calibration. Journal of Risk and Insurance, 73, 687–718.CrossRefGoogle Scholar
Cairns, A.J.G., Blake, D., Dowd, K., Coughlan, G.D., Epstein, D., Ong, A. & Balevich, I. (2009). A quantitative comparison of stochastic mortality models using data from England and Wales and the United States. North American Actuarial Journal, 13, 1–35.CrossRefGoogle Scholar
Clayton, D. & Schifflers, E. (1987a). Models for temporal variation in cancer rates. I: Age-period and age-cohort models. Statistics in Medicine, 6, 449–467.10.1002/sim.4780060405CrossRefGoogle Scholar
Clayton, D. & Schifflers, E. (1987b). Models for temporal variation in cancer rates. II: Age-period-cohort models. Statistics in Medicine, 6, 469–481.CrossRefGoogle ScholarPubMed
Continuous Mortality Investigation (2016a). CMI Mortality Projections Model consultation. Working Paper 90.Google Scholar
Continuous Mortality Investigation (2016b). CMI Mortality Projections Model consultation - technical paper. Working Paper 91.Google Scholar
Continuous Mortality Investigation (2016c). CMI Mortality Projections Model: Consultation, responses and plans for CMI $\_$ 2016. Working Paper 93.Google Scholar
Currie, I.D., Durban, M. & Eilers, P.H.C. (2004). Smoothing and forecasting mortality rates. Statistical Modelling, 4, 279–298.CrossRefGoogle Scholar
Currie, I.D. (2013). Smoothing constrained generalized linear models with an application to the Lee-Carter model. Statistical Modelling, 13, 69–93.CrossRefGoogle Scholar
Currie, I.D. (2016). On fitting generalized linear and non-linear models of mortality. Scandinavian Actuarial Journal, 2016, 356–383.CrossRefGoogle Scholar
Delwarde, A., Denuit, M. & Eilers, P. (2007). Smoothing the Lee-Carter and Poisson log-bilinear models for mortality forecasting: a penalized likelihood approach. Statistical Modelling, 7, 29–48.CrossRefGoogle Scholar
Eilers, P.H.C. & Marx, B.D. (1996). Flexible smoothing with B-splines and penalties. Statistical Science, 11, 89–121.CrossRefGoogle Scholar
Hunt, A. & Blake, D. (2020a). Identifiability in age/period mortality models. Annals of Actuarial Science, 14, 461–499.Google Scholar
Hunt, A. & Blake, D. (2020b). Identifiability in age/period/cohort mortality models. Annals of Actuarial Science, 14, 500–536.Google Scholar
Hunt, A. & Blake, D. (2020c). A Bayesian approach to modelling and forecasting cohort effects. North American Actuarial Journal.Google Scholar
Lee, R.D. & Carter, L.R. (1992). Modeling and forecasting U.S. mortality. Journal of the American Statistical Association, 87, 659–675.Google Scholar
Macdonald, A.S., Richards, S.J. & Currie, I.D. (2018). Modelling Mortality with Actuarial Applications. Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Nelder, J.A. & Wedderburn, R.W.M. (1972). Generalized linear models. Journal of the Royal Statistical Society: Series A, 135, 370–384.CrossRefGoogle Scholar
Plat, J. (2009). On stochastic mortality modeling. Insurance: Mathematics and Economics, 45, 393–404.Google Scholar
R Core Team (2018). R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.Google Scholar
Richards, S.J., Currie, I.D., Kleinow, T. & Ritchie, G.P. (to appear). A stochastic implementation of the APCI model for mortality projections. British Actuarial Journal.Google Scholar
Searle, S.R. (1982). Matrix Algebra Useful for Statistics. Wiley, New York.Google Scholar
Shumway, R.H. & Stoffer, D.S. (2017). Time Series Analysis and Its Applications: With R Examples. Springer, Berlin.CrossRefGoogle Scholar
Whittaker, E.T. (1923). On a new method of graduation. Proceedings of the Edinburgh Mathematical Society, 41, 63–75.Google Scholar