Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-24T00:25:43.460Z Has data issue: false hasContentIssue false
  • English
  • Français

Turán-type results for intersection graphs of boxes

Part of: Graph theory

Published online by Cambridge University Press:  19 May 2021

István Tomon  and
Dmitriy Zakharov
István Tomon*
Affiliation:
ETH Zurich, Zurich, Switzerland
Dmitriy Zakharov
Affiliation:
MIPTMoscow, Russia HSEMoscow, Russia
*
*Corresponding author. Email: istvan.tomon@math.ethz.ch
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this short note, we prove the following analog of the Kővári–Sós–Turán theorem for intersection graphs of boxes. If G is the intersection graph of n axis-parallel boxes in 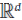$${{\mathbb{R}}^d}$$ such that G contains no copy of Kt,t, then G has at most ctn( log n)2d+3 edges, where c = c(d)>0 only depends on d. Our proof is based on exploring connections between boxicity, separation dimension and poset dimension. Using this approach, we also show that a construction of Basit, Chernikov, Starchenko, Tao and Tran of K2,2-free incidence graphs of points and rectangles in the plane can be used to disprove a conjecture of Alon, Basavaraju, Chandran, Mathew and Rajendraprasad. We show that there exist graphs of separation dimension 4 having superlinear number of edges.

MSC classification

Primary: 05C10: Planar graphs; geometric and topological aspects of graph theory 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 6 , November 2021 , pp. 982 - 987
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Adiga, A., Bhowmick, D. and Chandran, L. S. (2011) Boxicity and poset dimension. SIAM J. Discrete Math. 25 1687–1698.CrossRefGoogle Scholar
Alon, N., Basavaraju, M., Chandran, L. S., Mathew, R. and Rajendraprasad, D. (2018) Separation dimension and sparsity. J. Graph Theory 89 14–25.CrossRefGoogle Scholar
Basit, A., Chernikov, A., Starchenko, S., Tao, T. and Tran, C.-M. (2020) Zarankiewicz’s problem for semilinear hypergraphs. arXiv preprint, arXiv:2009.02922.Google Scholar
Davies, J. (2020) Box and segment intersection graphs with large girth and chromatic number. arXiv preprint, arXiv:2011.14174.Google Scholar
Fox, J. and Pach, J. (2008) Separator theorems and Turán-type results for planar intersection graph. Adv. Math. 219 1070–1080.CrossRefGoogle Scholar
Fox, J., Pach, J., Sheffer, A., Suk, A. and Zahl, J. (2017) A semi-algebraic version of Zarankiewicz’s problem. J. Eur. Math. Soc. 19 1785–1810.CrossRefGoogle Scholar
Janzer, O. and Pohoata, C. (2020) On the Zarankiewicz problem for graphs with bounded VC-dimension. arXiv preprint, arXiv:2009.00130.Google Scholar
Kostochka, A. V. (2004) Coloring intersection graphs of geometric figures with a given clique number. Contemp. Math. 342 127–138.CrossRefGoogle Scholar
Kövári, T., Sós, V. and Turán, P. (1954) On a problem of K. Zarankiewicz. Colloq. Math. 3 50–57.Google Scholar
Scott, A. and Wood, D. R. (2018) Separation dimension and degree. Math. Proc. Camb. Phil. Soc. 1–10.Google Scholar
Szemerédi, E. and Trotter, W. T. (1983) Extremal problems in discrete geometry. Combinatorica 3 381–392.CrossRefGoogle Scholar
Tomon, I. (2020) Ramsey properties of semilinear graphs. arXiv preprint, arXiv:2102.12464.Google Scholar