Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-23T06:05:09.061Z Has data issue: false hasContentIssue false
  • English
  • Français

ANALOGUES OF CENTRALIZER SUBALGEBRAS FOR FIAT 2-CATEGORIES AND THEIR 2-REPRESENTATIONS

Part of: Categories with structure Lie algebras and Lie superalgebras Representation theory of rings and algebras

Published online by Cambridge University Press:  04 December 2018

Marco Mackaay Open the ORCID record for Marco Mackaay [Opens in a new window] ,
Volodymyr Mazorchuk Open the ORCID record for Volodymyr Mazorchuk [Opens in a new window] ,
Vanessa Miemietz  and
Xiaoting Zhang Open the ORCID record for Xiaoting Zhang [Opens in a new window]
Marco Mackaay
Affiliation:
Center for Mathematical Analysis, Geometry, and Dynamical Systems, Departamento de Matemática, Instituto Superior Técnico, 1049-001Lisboa, Portugal Departamento de Matemática, FCT, Universidade do Algarve, Campus de Gambelas, 8005-139Faro, Portugal (mmackaay@ualg.pt)
Volodymyr Mazorchuk
Affiliation:
Department of Mathematics, Uppsala University, Box. 480, SE-75106, Uppsala, Sweden (mazor@math.uu.se)
Vanessa Miemietz
Affiliation:
School of Mathematics, University of East Anglia, NorwichNR4 7TJ, UK (v.miemietz@uea.ac.uk)
Xiaoting Zhang
Affiliation:
Department of Mathematics, Uppsala University, Box. 480, SE-75106, Uppsala, Sweden (xiaoting.zhang@math.uu.se)
Get access Rights & Permissions [Opens in a new window]

Abstract

The main result of this paper establishes a bijection between the set of equivalence classes of simple transitive 2-representations with a fixed apex 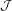${\mathcal{J}}$ of a fiat 2-category 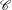$\mathscr{C}$ and the set of equivalence classes of faithful simple transitive 2-representations of the fiat 2-subquotient of 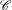$\mathscr{C}$ associated with a diagonal 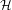${\mathcal{H}}$-cell in 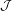${\mathcal{J}}$. As an application, we classify simple transitive 2-representations of various categories of Soergel bimodules, in particular, completing the classification in types 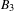$B_{3}$ and 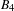$B_{4}$.

Keywords

2-categorysimple transitive 2-representationGreen relationscoalgebra 1-morphismcotensor product

MSC classification

Primary: 18D05: Double categories, $2$-categories, bicategories and generalizations
Secondary: 16G99: None of the above, but in this section 17B99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 6 , November 2020 , pp. 1793 - 1829
Check for updates
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agerholm, T. and Mazorchuk, V., On selfadjoint functors satisfying polynomial relations, J. Algebra 330 (2011), 448–467.Google Scholar
Auslander, M., Representation theory of Artin algebras. I, II, Comm. Algebra 1 (1974), 177–268. ibid. 1 (1974), 269–310.Google Scholar
Bernstein, J., Frenkel, I. and Khovanov, M., A categorification of the Temperley-Lieb algebra and Schur quotients of U (sl2) via projective and Zuckerman functors, Selecta Math. (N.S.) 5(2) (1999), 199–241.Google Scholar
Björner, A. and Brenti, F., Combinatorics of Coxeter Groups, Graduate Texts in Mathematics, Volume 231 (Springer, New York, 2005).Google Scholar
Chan, A. and Mazorchuk, V., Diagrams and discrete extensions for finitary 2-representations, Math. Proc. Cambr. Phil. Soc. (to appear) Preprint, 2016, arXiv:1601.00080; doi:10.1017/S0305004117000858.Google Scholar
Chuang, J. and Rouquier, R., Derived equivalences for symmetric groups and sl2 -categorification, Ann. of Math. (2) 167(1) (2008), 245–298.Google Scholar
Clifford, A., Matrix representations of completely simple semigroups, Amer. J. Math. 64 (1942), 327–342.Google Scholar
Elias, B. and Williamson, G., The Hodge theory of Soergel bimodules, Ann. of Math. (2) 180(3) (2014), 1089–1136.Google Scholar
Etingof, P., Gelaki, S., Nikshych, D. and Ostrik, V., Tensor Categories, Mathematical Surveys and Monographs, Volume 205 (American Mathematical Society, Providence, RI, 2015).Google Scholar
Etingof, P., Nikshych, D. and Ostrik, V., On fusion categories, Ann. of Math. (2) 162(2) (2005), 581–642.Google Scholar
Etingof, P. and Ostrik, V., Finite tensor categories, Mosc. Math. J. 4(3) (2004), 627–654, 782–783.Google Scholar
Ganyushkin, O., Mazorchuk, V. and Steinberg, B., On the irreducible representations of a finite semigroup, Proc. Amer. Math. Soc. 137(11) (2009), 3585–3592.Google Scholar
Green, R. and Losonczy, J., Fully commutative Kazhdan–Lusztig cells, Ann. Inst. Fourier (Grenoble) 51(4) (2001), 1025–1045.Google Scholar
Grensing, A. L. and Mazorchuk, V., Categorification of the Catalan monoid, Semigroup Forum 89(1) (2014), 155–168.Google Scholar
Grensing, A. L. and Mazorchuk, V., Categorification using dual projection functors, Commun. Contemp. Math. 19(3) (2017), 1650016, 40 pp.Google Scholar
Kazhdan, D. and Lusztig, G., Representations of Coxeter groups and Hecke algebras, Invent. Math. 53(2) (1979), 165–184.Google Scholar
Kelly, G., Doctrinal adjunction, in Category Seminar (Proc. Sem., Sydney, 1972/1973), Lecture Notes in Mathematics, Volume 420, pp. 257–280 (Springer, Berlin, 1974).Google Scholar
Khomenko, O. and Mazorchuk, V., On Arkhipov’s and Enright’s functors, Math. Z. 249(2) (2005), 357–386.Google Scholar
Khovanov, M. and Lauda, A., A categorification of a quantum sln, Quantum Topol. 1 (2010), 1–92.Google Scholar
Kildetoft, T. and Mazorchuk, V., Special modules over positively based algebras, Documenta Math. 21 (2016), 1171–1192.Google Scholar
Kildetoft, T., Mackaay, M., Mazorchuk, V. and Zimmermann, J., Simple transitive 2-representations of small quotients of Soergel bimodules, Trans. Amer. Math. Soc. (to appear) Preprint, 2016, arXiv:1605.01373; doi:10.1090/tran/7456.Google Scholar
Leinster, T., Basic bicategories, Preprint, arXiv:math/9810017.Google Scholar
Lusztig, G., Cells in affine Weyl groups, in Algebraic Groups and Related Topics (Kyoto/Nagoya, 1983), Advanced Studies in Pure Mathematics, Volume 6, pp. 255–287 (North-Holland, Amsterdam, 1985).Google Scholar
Mac Lane, S., Categories for the Working Mathematician, Graduate Texts in Mathematics, Volume 5 (Springer, New York, 1971).Google Scholar
Mackaay, M. and Mazorchuk, V., Simple transitive 2-representations for some 2-subcategories of Soergel bimodules, J. Pure Appl. Algebra 221(3) (2017), 565–587.Google Scholar
Mackaay, M. and Tubbenhauer, D., Two-color Soergel calculus and simple transitive 2-representations, Canad. J. Math. (to appear) Preprint, 2016, arXiv:1609.00962; doi:10.4153/CJM-2017-061-2.Google Scholar
Mackaay, M., Mazorchuk, V., Miemietz, V. and Tubbenhauer, D., Simple transitive 2-representations via (co)algebra 1-morphism, Indiana Univ. Math. J. (to appear) Preprint, 2016, arXiv:1612.06325.Google Scholar
Mazorchuk, V., Lectures on Algebraic Categorification, QGM Master Class Series, (European Mathematical Society (EMS), Zurich, 2012).Google Scholar
Mazorchuk, V., Classification problems in 2-representation theory, São Paulo J. Math. Sci. 11(1) (2017), 1–22.Google Scholar
Mazorchuk, V. and Miemietz, V., Cell 2-representations of finitary 2-categories, Compositio Math. 147 (2011), 1519–1545.Google Scholar
Mazorchuk, V. and Miemietz, V., Additive versus abelian 2-representations of fiat 2-categories, Moscow Math. J. 14(3) (2014), 595–615.Google Scholar
Mazorchuk, V. and Miemietz, V., Endmorphisms of cell 2-representations, Int. Math. Res. Notes, 2016, 24, 7471–7498.Google Scholar
Mazorchuk, V. and Miemietz, V., Morita theory for finitary 2-categories, Quantum Topol. 7(1) (2016), 1–28.Google Scholar
Mazorchuk, V. and Miemietz, V., Transitive 2-representations of finitary 2-categories, Trans. Amer. Math. Soc. 368(11) (2016), 7623–7644.Google Scholar
Mazorchuk, V. and Miemietz, V., Isotypic faithful 2-representations of 𝓙-simple fiat 2-categories, Math. Z. 282(1-2) (2016), 411–434.Google Scholar
Mazorchuk, V., Miemietz, V. and Zhang, X., Characterisation and applications of $\Bbbk$-split bimodules, Math. Scand. (to appear) Preprint, 2017, arXiv:1701.03025.Google Scholar
Mazorchuk, V., Miemietz, V. and Zhang, X., Pyramids and 2-representations, Preprint 2017, arXiv:1705.03174.Google Scholar
Mazorchuk, V. and Zhang, X., Simple transitive 2-representations for two non-fiat 2-categories of projective functors, Ukr. Math. J. (to appear) Preprint, 2016, arXiv:1601.00097.Google Scholar
Mazorchuk, V. and Zhang, X., Bimodules over uniformly oriented $A_{n}$ quivers with radical square zero, Kyoto J. Math. (to appear) Preprint, 2017, arXiv:1703.08377.Google Scholar
Munn, W., Matrix representations of semigroups, Proc. Cambridge Philos. Soc. 53 (1951), 5–12.Google Scholar
Ostrik, V., Module categories, weak Hopf algebras and modular invariants, Transform. Groups 8(2) (2003), 177–206.Google Scholar
Ponizovskiï, I., On matrix representations of associative systems, Mat. Sb. N.S. 38 (1956), 241–260.Google Scholar
Rouquier, R., 2-Kac-Moody algebras, Preprint, 2008, arXiv:0812.5023.Google Scholar
Soergel, W., The combinatorics of Harish-Chandra bimodules, J. Reine Angew. Math. 429 (1992), 49–74.Google Scholar
Soergel, W., Kazhdan–Lusztig-Polynome und unzerlegbare Bimoduln über Polynomringen, J. Inst. Math. Jussieu 6(3) (2007), 501–525.Google Scholar
Stembridge, J., On the fully commutative elements of Coxeter groups, J. Algebraic Combin. 5(4) (1996), 353–385.Google Scholar
Takeuchi, M., Morita theorems for categories of comodules, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 24(3) (1977), 629–644.Google Scholar
Xantcha, Q., Gabriel 2-quivers for finitary 2-categories, J. Lond. Math. Soc. (2) 92(3) (2015), 615–632.Google Scholar
Zhang, X., Duflo involutions for 2-categories associated to tree quivers, J. Algebra Appl. 15(3) (2016), 1650041, 25 pp.Google Scholar
Zhang, X., Simple transitive 2-representations and Drinfeld center for some finitary 2-categories, J. Pure Appl. Algebra 222 (2018), 97–130.Google Scholar
Zimmermann, J., Simple transitive 2-representations of Soergel bimodules in type B 2, J. Pure Appl. Algebra 221(3) (2017), 666–690.Google Scholar
Zimmermann, J., Simple transitive 2-representations of some 2-categories of projective functors, Beitr. Algebra Geom. 59(1) (2018), 41–50.Google Scholar