Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-24T10:09:25.169Z Has data issue: false hasContentIssue false
  • English
  • Français

WIGNER’S THEOREM IN 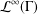${\mathcal{L}}^{\infty }(\unicode[STIX]{x1D6E4})$-TYPE SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  04 December 2017

WEIKE JIA  and
DONGNI TAN Open the ORCID record for DONGNI TAN [Opens in a new window]
WEIKE JIA
Affiliation:
Department of Mathematics, Tianjin University of Technology, 300384 Tianjin, China email jiaweike2017@163.com
DONGNI TAN*
Affiliation:
Department of Mathematics, Tianjin University of Technology, 300384 Tianjin, China email tandongni0608@sina.cn
*
✉tandongni0608@sina.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate surjective solutions of the functional equation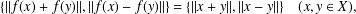

$$\begin{eqnarray}\displaystyle \{\Vert f(x)+f(y)\Vert ,\Vert f(x)-f(y)\Vert \}=\{\Vert x+y\Vert ,\Vert x-y\Vert \}\quad (x,y\in X), & & \displaystyle \nonumber\end{eqnarray}$$
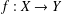where $f:X\rightarrow Y$ is a map between two real 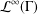${\mathcal{L}}^{\infty }(\unicode[STIX]{x1D6E4})$-type spaces. We show that all such solutions are phase equivalent to real linear isometries. This can be considered as an extension of Wigner’s theorem on symmetry for real 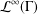${\mathcal{L}}^{\infty }(\unicode[STIX]{x1D6E4})$-type spaces.

Keywords

L∞(𝛤)-type spacesWigner’s theoremphase equivalent

MSC classification

Primary: 46B03: Isomorphic theory (including renorming) of Banach spaces
Secondary: 46B04: Isometric theory of Banach spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 279 - 284
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors are supported by the Natural Science Foundation of China, Grant Nos. 11371201, 11201337, 11201338 and 11301384.

References

Gehér, Gy. P., ‘An elementary proof for the non-bijective version of Wigner’s theorem’, Phys. Lett. A 378 (2014), 2054–2057.Google Scholar
Györy, M., ‘A new proof of Wigner’s theorem’, Rep. Math. Phys. 54 (2004), 159–167.Google Scholar
Huang, X. and Tan, D., ‘Wigner’s theorem in atomic L p -spaces (p > 0)’, Publ. Math. Debrecen , to appear.+0)’,+Publ.+Math.+Debrecen+,+to+appear.>Google Scholar
Maksa, G. and Páles, Z., ‘Wigner’s theorem revisited’, Publ. Math. Debrecen 81(1–2) (2012), 243–249.Google Scholar
Mazur, S. and Ulam, S., ‘Sur les transformations isométriques d’espaces vectoriels normés’, C. R. Math. Acad. Sci. Paris 194 (1932), 946–948.Google Scholar
Molnár, L., ‘Orthogonality preserving transformations on indefinite inner product spaces: generalization of Uhlhorn’s version of Wigner’s theorem’, J. Funct. Anal. 194(2) (2002), 248–262.CrossRefGoogle Scholar
Mouchet, A., ‘An alternative proof of Wigner theorem on quantum transformations based on elementary complex analysis’, Phys. Lett. A 377 (2013), 2709–2711.Google Scholar
Rätz, J., ‘On Wigner’s theorem: remarks, complements, comments, and corollaries’, Aequationes Math. 52(1–2) (1996), 1–9.Google Scholar
Sharma, C. S. and Almeida, D. L., ‘A direct proof of Wigner’s theorem on maps which preserve transition probabilities between pure states of quantum systems’, Ann. Phys. 197(2) (1990), 300–309.Google Scholar
Simon, R., Mukunda, N., Chaturvedi, S. and Srinivasan, V., ‘Two elementary proofs of the Wigner theorem on symmetry in quantum mechanics’, Phys. Lett. A 372(46) (2008), 6847–6852.Google Scholar
Tan, D. N., ‘Nonexpansive mappings on the unit spheres of some Banach spaces’, Bull. Aust. Math. Soc. 80 (2009), 139–146.Google Scholar
Turnšek, A., ‘A variant of Wigner’s functional equation’, Aequationes Math. 89(4) (2015), 1–8.Google Scholar