Article contents
Central limit theorems for coupled particle filters
Published online by Cambridge University Press: 24 September 2020
Abstract
In this article we prove new central limit theorems (CLTs) for several coupled particle filters (CPFs). CPFs are used for the sequential estimation of the difference of expectations with respect to filters which are in some sense close. Examples include the estimation of the filtering distribution associated to different parameters (finite difference estimation) and filters associated to partially observed discretized diffusion processes (PODDP) and the implementation of the multilevel Monte Carlo (MLMC) identity. We develop new theory for CPFs, and based upon several results, we propose a new CPF which approximates the maximal coupling (MCPF) of a pair of predictor distributions. In the context of ML estimation associated to PODDP with time-discretization 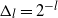 $\Delta_l=2^{-l}$
,
$\Delta_l=2^{-l}$
, 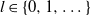 $l\in\{0,1,\dots\}$
, we show that the MCPF and the approach of Jasra, Ballesio, et al. (2018) have, under certain assumptions, an asymptotic variance that is bounded above by an expression that is of (almost) the order of
$l\in\{0,1,\dots\}$
, we show that the MCPF and the approach of Jasra, Ballesio, et al. (2018) have, under certain assumptions, an asymptotic variance that is bounded above by an expression that is of (almost) the order of 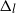 $\Delta_l$
(
$\Delta_l$
(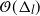 $\mathcal{O}(\Delta_l)$
), uniformly in time. The
$\mathcal{O}(\Delta_l)$
), uniformly in time. The 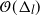 $\mathcal{O}(\Delta_l)$
bound preserves the so-called forward rate of the diffusion in some scenarios, which is not the case for the CPF in Jasra et al. (2017).
$\mathcal{O}(\Delta_l)$
bound preserves the so-called forward rate of the diffusion in some scenarios, which is not the case for the CPF in Jasra et al. (2017).
- Type
- Original Article
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 6
- Cited by





