Generalized Algebraic Data Types (GADTs) are a syntactic generalization of the usual algebraic data types (ADTs), such as lists, trees, etc. ADTs’ standard initial algebra semantics (IAS) in the category  of sets justify critical syntactic constructs – such as recursion, pattern matching, and fold – for programming with them. In this paper, we show that semantics for GADTs that specialize to the IAS for ADTs are necessarily unsatisfactory. First, we show that the functorial nature of such semantics for GADTs in
of sets justify critical syntactic constructs – such as recursion, pattern matching, and fold – for programming with them. In this paper, we show that semantics for GADTs that specialize to the IAS for ADTs are necessarily unsatisfactory. First, we show that the functorial nature of such semantics for GADTs in  introduces ghost elements, i.e., elements not writable in syntax. Next, we show how such ghost elements break parametricity. We observe that the situation for GADTs contrasts dramatically with that for ADTs, whose IAS coincides with the parametric model constructed via their Church encodings in System F. Our analysis reveals that the fundamental obstacle to giving a functorial IAS for GADTs is the inherently partial nature of their map functions. We show that this obstacle cannot be overcome by replacing
introduces ghost elements, i.e., elements not writable in syntax. Next, we show how such ghost elements break parametricity. We observe that the situation for GADTs contrasts dramatically with that for ADTs, whose IAS coincides with the parametric model constructed via their Church encodings in System F. Our analysis reveals that the fundamental obstacle to giving a functorial IAS for GADTs is the inherently partial nature of their map functions. We show that this obstacle cannot be overcome by replacing  with other categories that account for this partiality.
with other categories that account for this partiality.
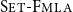 ) order-preserving logics are non-algebraizable self-extensional logics of formal inconsistency and undeterminedness determined by a six-valued matrix. We studied these logics extensively in Gomes et al. ((2022).
) order-preserving logics are non-algebraizable self-extensional logics of formal inconsistency and undeterminedness determined by a six-valued matrix. We studied these logics extensively in Gomes et al. ((2022).  order-preserving and
order-preserving and 