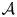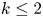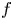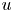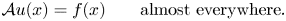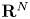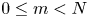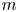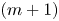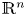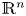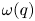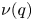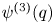Let 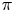 be a discrete group, and let
be a discrete group, and let 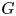 be a compact-connected Lie group. Then, there is a map
be a compact-connected Lie group. Then, there is a map 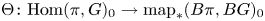 between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for
between the null components of the spaces of homomorphisms and based maps, which sends a homomorphism to the induced map between classifying spaces. Atiyah and Bott studied this map for 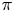 a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map
a surface group, and showed that it is surjective in rational cohomology. In this paper, we prove that the map 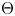 is surjective in rational cohomology for
is surjective in rational cohomology for 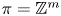 and the classical group
and the classical group 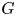 except for
except for 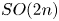 , and that it is not surjective for
, and that it is not surjective for 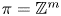 with
with 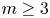 and
and 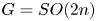 with
with 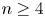 . As an application, we consider the surjectivity of the map
. As an application, we consider the surjectivity of the map 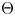 in rational cohomology for
in rational cohomology for 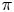 a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map
a finitely generated nilpotent group. We also consider the dimension of the cokernel of the map 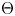 in rational homotopy groups for
in rational homotopy groups for 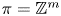 and the classical groups
and the classical groups 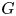 except for
except for 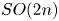 .
.