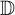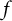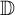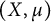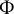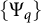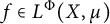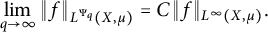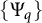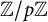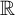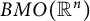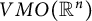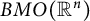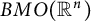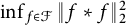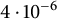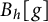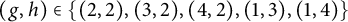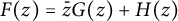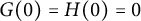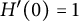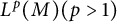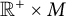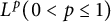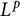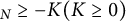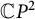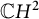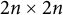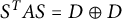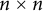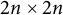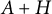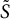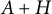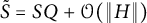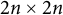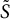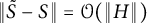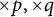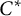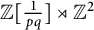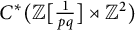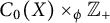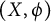Williamson’s theorem states that for any  real positive definite matrix A, there exists a
real positive definite matrix A, there exists a 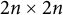 real symplectic matrix S such that
real symplectic matrix S such that 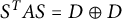 , where D is an
, where D is an 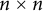 diagonal matrix with positive diagonal entries known as the symplectic eigenvalues of A. Let H be any
diagonal matrix with positive diagonal entries known as the symplectic eigenvalues of A. Let H be any 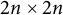 real symmetric matrix such that the perturbed matrix
real symmetric matrix such that the perturbed matrix 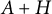 is also positive definite. In this paper, we show that any symplectic matrix
is also positive definite. In this paper, we show that any symplectic matrix 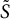 diagonalizing
diagonalizing 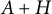 in Williamson’s theorem is of the form
in Williamson’s theorem is of the form 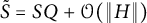 , where Q is a
, where Q is a 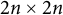 real symplectic as well as orthogonal matrix. Moreover, Q is in symplectic block diagonal form with the block sizes given by twice the multiplicities of the symplectic eigenvalues of A. Consequently, we show that
real symplectic as well as orthogonal matrix. Moreover, Q is in symplectic block diagonal form with the block sizes given by twice the multiplicities of the symplectic eigenvalues of A. Consequently, we show that 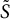 and S can be chosen so that
and S can be chosen so that 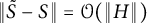 . Our results hold even if A has repeated symplectic eigenvalues. This generalizes the stability result of symplectic matrices for non-repeated symplectic eigenvalues given by Idel, Gaona, and Wolf [Linear Algebra Appl., 525:45–58, 2017].
. Our results hold even if A has repeated symplectic eigenvalues. This generalizes the stability result of symplectic matrices for non-repeated symplectic eigenvalues given by Idel, Gaona, and Wolf [Linear Algebra Appl., 525:45–58, 2017].
]]>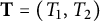 and investigate nontrivial invariant subspaces between the generalized spherical Aluthge transform of the linear pencil of
and investigate nontrivial invariant subspaces between the generalized spherical Aluthge transform of the linear pencil of 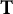 and the linear pencil of the original pair
and the linear pencil of the original pair 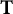 of bounded operators with dense ranges.
of bounded operators with dense ranges.