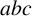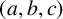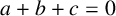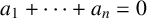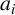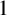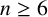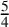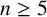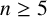Jones [‘Two subfactors and the algebraic decomposition of bimodules over  factors’, Acta Math. Vietnam 33(3) (2008), 209–218] proposed the study of ‘two subfactors’ of a
factors’, Acta Math. Vietnam 33(3) (2008), 209–218] proposed the study of ‘two subfactors’ of a  factor as a quantization of two closed subspaces in a Hilbert space. Motivated by this, we initiate a systematic study of a special class of two subfactors, namely a pair of spin model subfactors. We characterize which pairs of distinct complex Hadamard matrices in
factor as a quantization of two closed subspaces in a Hilbert space. Motivated by this, we initiate a systematic study of a special class of two subfactors, namely a pair of spin model subfactors. We characterize which pairs of distinct complex Hadamard matrices in  give rise to distinct spin model subfactors. Then, a detailed investigation is carried out for
give rise to distinct spin model subfactors. Then, a detailed investigation is carried out for  , where the spin model subfactors correspond to
, where the spin model subfactors correspond to  -actions on the hyperfinite type
-actions on the hyperfinite type  factor R. We observe that the intersection of the pair of spin model subfactors in this case is a nonirreducible vertex model subfactor and we characterize it as a diagonal subfactor. A few key invariants for the pair of spin model subfactors are computed to understand their relative positions.
factor R. We observe that the intersection of the pair of spin model subfactors in this case is a nonirreducible vertex model subfactor and we characterize it as a diagonal subfactor. A few key invariants for the pair of spin model subfactors are computed to understand their relative positions.