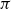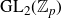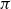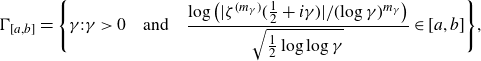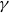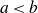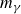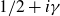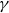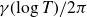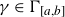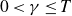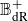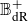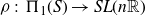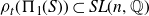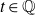We study a pair consisting of a smooth 3-fold defined over an algebraically closed field and a “general”  -ideal. We show that the minimal log discrepancy (“mld” for short) of every such a pair is computed by a prime divisor obtained by at most two weighted blow-ups. This bound is regarded as a weighted blow-up version of Mustaţă–Nakamura’s conjecture. We also show that if the mld of such a pair is not less than 1, then it is computed by at most one weighted blow-up. As a consequence, ACC of mld holds for such pairs.
-ideal. We show that the minimal log discrepancy (“mld” for short) of every such a pair is computed by a prime divisor obtained by at most two weighted blow-ups. This bound is regarded as a weighted blow-up version of Mustaţă–Nakamura’s conjecture. We also show that if the mld of such a pair is not less than 1, then it is computed by at most one weighted blow-up. As a consequence, ACC of mld holds for such pairs.