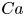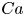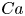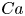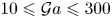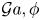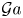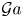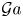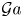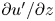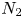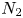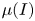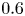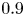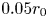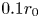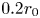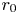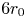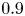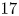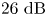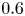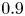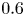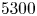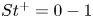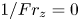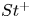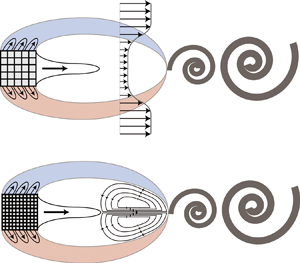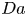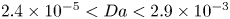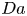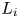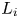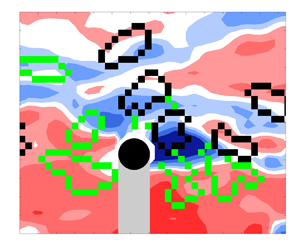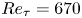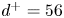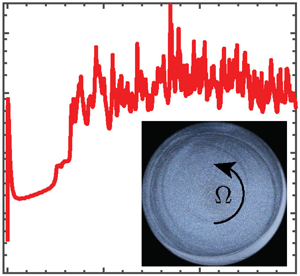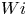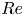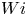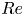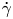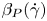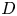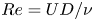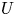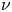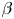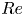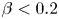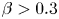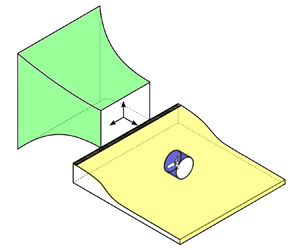
The aeroacoustics of a boundary layer ingesting (BLI) ducted fan is investigated experimentally. The study examines a ducted fan immersed in an adverse streamwise pressure gradient turbulent boundary layer developed over a curved wall. Aeroacoustics measurements indicate that the noise from the BLI ducted fan results from a complex interaction among the fan, duct and the incoming boundary layer. The fundamental mechanisms of noise generation are explained using a general source separation strategy. A detailed noise comparison is made at varying fan rotational speeds and across a wide range of axial inflow velocities. In a low thrust regime, the noise is found to be driven by the fan loading, coupled with duct acoustics and the haystacking phenomenon. In a high thrust regime, the contribution from duct acoustics diminishes, and the noise is predominantly driven by the fan loading coupled with the haystacking phenomenon.