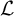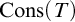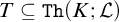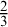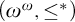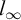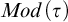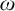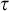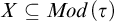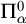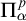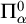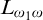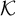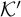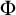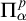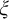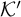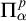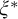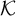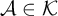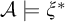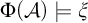We study the parameterized complexity of the problem to decide whether a given natural number n satisfies a given  -formula
-formula  ; the parameter is the size of
; the parameter is the size of  . This parameterization focusses attention on instances where n is large compared to the size of
. This parameterization focusses attention on instances where n is large compared to the size of  . We show unconditionally that this problem does not belong to the parameterized analogue of
. We show unconditionally that this problem does not belong to the parameterized analogue of  . From this we derive that certain natural upper bounds on the complexity of our parameterized problem imply certain separations of classical complexity classes. This connection is obtained via an analysis of a parameterized halting problem. Some of these upper bounds follow assuming that
. From this we derive that certain natural upper bounds on the complexity of our parameterized problem imply certain separations of classical complexity classes. This connection is obtained via an analysis of a parameterized halting problem. Some of these upper bounds follow assuming that  proves the MRDP theorem in a certain weak sense.
proves the MRDP theorem in a certain weak sense.