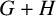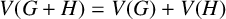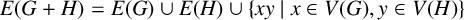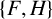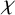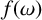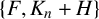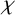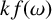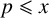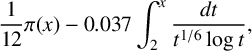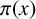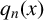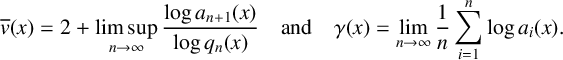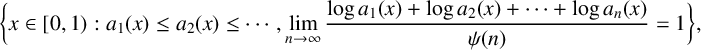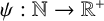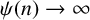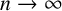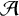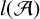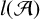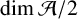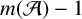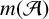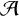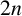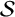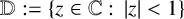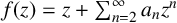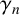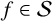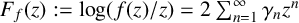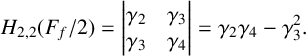We consider the pseudorelativistic Hartree equation
which describes the dynamics of pseudorelativistic boson stars in the mean-field limit. We study the travelling waves of the form  , where
, where  denotes the travelling velocity. We prove that
denotes the travelling velocity. We prove that  converges strongly to the minimiser
converges strongly to the minimiser  of the limit energy
of the limit energy  in
in  as the light speed
as the light speed  , where
, where  is the corresponding energy for the limit equation
is the corresponding energy for the limit equation
Since the operator  is the classical kinetic operator, we call this the nonrelativistic limit. We prove the existence of the minimiser for the limit energy
is the classical kinetic operator, we call this the nonrelativistic limit. We prove the existence of the minimiser for the limit energy  by using concentration-compactness arguments.
by using concentration-compactness arguments.
]]> The parameters of these codes are explored for small matrix orders and weights.
The parameters of these codes are explored for small matrix orders and weights.