For each uniformity 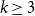 , we construct
, we construct 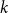 uniform linear hypergraphs
uniform linear hypergraphs 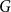 with arbitrarily large maximum degree
with arbitrarily large maximum degree 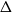 whose independence polynomial
whose independence polynomial 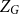 has a zero
has a zero 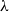 with
with 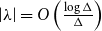 . This disproves a recent conjecture of Galvin, McKinley, Perkins, Sarantis, and Tetali.
. This disproves a recent conjecture of Galvin, McKinley, Perkins, Sarantis, and Tetali.
For each uniformity 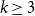 , we construct
, we construct 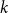 uniform linear hypergraphs
uniform linear hypergraphs 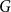 with arbitrarily large maximum degree
with arbitrarily large maximum degree 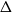 whose independence polynomial
whose independence polynomial 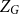 has a zero
has a zero 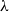 with
with 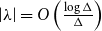 . This disproves a recent conjecture of Galvin, McKinley, Perkins, Sarantis, and Tetali.
. This disproves a recent conjecture of Galvin, McKinley, Perkins, Sarantis, and Tetali.
In the last two decades the study of random instances of constraint satisfaction problems (CSPs) has flourished across several disciplines, including computer science, mathematics and physics. The diversity of the developed methods, on the rigorous and non-rigorous side, has led to major advances regarding both the theoretical as well as the applied viewpoints. Based on a ceteris paribus approach in terms of the density evolution equations known from statistical physics, we focus on a specific prominent class of regular CSPs, the so-called occupation problems, and in particular on  -in-
-in-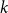 occupation problems. By now, out of these CSPs only the satisfiability threshold – the largest degree for which the problem admits asymptotically a solution – for the
occupation problems. By now, out of these CSPs only the satisfiability threshold – the largest degree for which the problem admits asymptotically a solution – for the 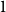 -in-
-in-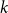 occupation problem has been rigorously established. Here we determine the satisfiability threshold of the
occupation problem has been rigorously established. Here we determine the satisfiability threshold of the 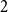 -in-
-in-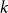 occupation problem for all
occupation problem for all 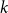 . In the proof we exploit the connection of an associated optimization problem regarding the overlap of satisfying assignments to a fixed point problem inspired by belief propagation, a message passing algorithm developed for solving such CSPs.
. In the proof we exploit the connection of an associated optimization problem regarding the overlap of satisfying assignments to a fixed point problem inspired by belief propagation, a message passing algorithm developed for solving such CSPs.
This paper initiates the explicit study of face numbers of matroid polytopes and their computation. We prove that, for the large class of split matroid polytopes, their face numbers depend solely on the number of cyclic flats of each rank and size, together with information on the modular pairs of cyclic flats. We provide a formula which allows us to calculate  -vectors without the need of taking convex hulls or computing face lattices. We discuss the particular cases of sparse paving matroids and rank two matroids, which are of independent interest due to their appearances in other combinatorial and geometric settings.
-vectors without the need of taking convex hulls or computing face lattices. We discuss the particular cases of sparse paving matroids and rank two matroids, which are of independent interest due to their appearances in other combinatorial and geometric settings.
In this note, we formulate a ‘one-sided’ version of Wormald’s differential equation method. In the standard ‘two-sided’ method, one is given a family of random variables that evolve over time and which satisfy some conditions, including a tight estimate of the expected change in each variable over one-time step. These estimates for the expected one-step changes suggest that the variables ought to be close to the solution of a certain system of differential equations, and the standard method concludes that this is indeed the case. We give a result for the case where instead of a tight estimate for each variable’s expected one-step change, we have only an upper bound. Our proof is very simple and is flexible enough that if we instead assume tight estimates on the variables, then we recover the conclusion of the standard differential equation method.
]]>A tantalizing open problem, posed independently by Stiebitz in 1995 and by Alon in 1996 and again in 2006, asks whether for every pair of integers 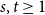 there exists a finite number
there exists a finite number 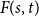 such that the vertex set of every digraph of minimum out-degree at least
such that the vertex set of every digraph of minimum out-degree at least 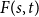 can be partitioned into non-empty parts
can be partitioned into non-empty parts 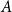 and
and 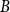 such that the subdigraphs induced on
such that the subdigraphs induced on 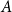 and
and 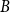 have minimum out-degree at least
have minimum out-degree at least  and
and 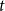 , respectively.
, respectively.
In this short note, we prove that if 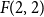 exists, then all the numbers
exists, then all the numbers 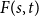 with
with 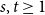 exist and satisfy
exist and satisfy 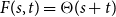 . In consequence, the problem of Alon and Stiebitz reduces to the case
. In consequence, the problem of Alon and Stiebitz reduces to the case 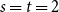 . Moreover, the numbers
. Moreover, the numbers 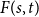 with
with 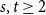 either all exist and grow linearly, or all of them do not exist.
either all exist and grow linearly, or all of them do not exist.
In this paper, we study discrepancy questions for spanning subgraphs of 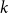 -uniform hypergraphs. Our main result is that, for any integers
-uniform hypergraphs. Our main result is that, for any integers 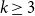 and
and 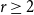 , any
, any  -colouring of the edges of a
-colouring of the edges of a 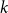 -uniform
-uniform  -vertex hypergraph
-vertex hypergraph 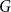 with minimum
with minimum 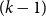 -degree
-degree 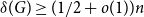 contains a tight Hamilton cycle with high discrepancy, that is, with at least
contains a tight Hamilton cycle with high discrepancy, that is, with at least 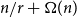 edges of one colour. The minimum degree condition is asymptotically best possible and our theorem also implies a corresponding result for perfect matchings. Our tools combine various structural techniques such as Turán-type problems and hypergraph shadows with probabilistic techniques such as random walks and the nibble method. We also propose several intriguing problems for future research.
edges of one colour. The minimum degree condition is asymptotically best possible and our theorem also implies a corresponding result for perfect matchings. Our tools combine various structural techniques such as Turán-type problems and hypergraph shadows with probabilistic techniques such as random walks and the nibble method. We also propose several intriguing problems for future research.
We study several basic problems about colouring the 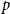 -random subgraph
-random subgraph 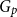 of an arbitrary graph
of an arbitrary graph 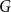 , focusing primarily on the chromatic number and colouring number of
, focusing primarily on the chromatic number and colouring number of 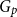 . In particular, we show that there exist infinitely many
. In particular, we show that there exist infinitely many 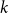 -regular graphs
-regular graphs 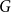 for which the colouring number (i.e., degeneracy) of
for which the colouring number (i.e., degeneracy) of 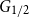 is at most
is at most 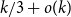 with high probability, thus disproving the natural prediction that such random graphs must have colouring number at least
with high probability, thus disproving the natural prediction that such random graphs must have colouring number at least 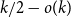 .
.
We show that every 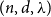 -graph contains a Hamilton cycle for sufficiently large
-graph contains a Hamilton cycle for sufficiently large  , assuming that
, assuming that 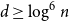 and
and 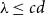 , where
, where 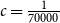 . This significantly improves a recent result of Glock, Correia, and Sudakov, who obtained a similar result for
. This significantly improves a recent result of Glock, Correia, and Sudakov, who obtained a similar result for 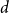 that grows polynomially with
that grows polynomially with  . The proof is based on a new result regarding the second largest eigenvalue of the adjacency matrix of a subgraph induced by a random subset of vertices, combined with a recent result on connecting designated pairs of vertices by vertex-disjoint paths in
. The proof is based on a new result regarding the second largest eigenvalue of the adjacency matrix of a subgraph induced by a random subset of vertices, combined with a recent result on connecting designated pairs of vertices by vertex-disjoint paths in 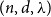 -graphs. We believe that the former result is of independent interest and will have further applications.
-graphs. We believe that the former result is of independent interest and will have further applications.