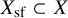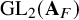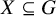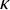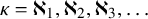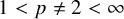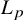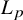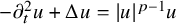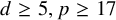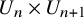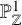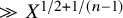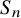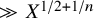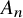We prove for the first time that knot Floer homology and Khovanov homology can detect non-fibered knots and that HOMFLY homology detects infinitely many knots; these theories were previously known to detect a mere six knots, all fibered. These results rely on our main technical theorem, which gives a complete classification of genus-1 knots in the 3-sphere whose knot Floer homology in the top Alexander grading is 2-dimensional. We discuss applications of this classification to problems in Dehn surgery which are carried out in two sequels. These include a proof that 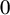 -surgery characterizes infinitely many knots, generalizing results of Gabai from his 1987 resolution of the Property R Conjecture.
-surgery characterizes infinitely many knots, generalizing results of Gabai from his 1987 resolution of the Property R Conjecture.
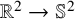
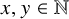
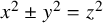
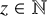
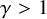
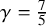
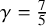
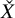
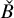
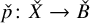
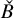
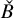
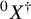 introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part
introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part