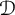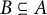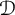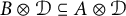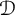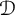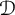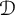This article aims to establish fractional Sobolev trace inequalities, logarithmic Sobolev trace inequalities, and Hardy trace inequalities associated with time-space fractional heat equations. The key steps involve establishing dedicated estimates for the fractional heat kernel, regularity estimates for the solution of the time-space fractional equations, and characterizing the norm of  in terms of the solution
in terms of the solution  . Additionally, fractional logarithmic Gagliardo–Nirenberg inequalities are proven, leading to
. Additionally, fractional logarithmic Gagliardo–Nirenberg inequalities are proven, leading to  logarithmic Sobolev inequalities for
logarithmic Sobolev inequalities for  . As a byproduct, Sobolev affine trace-type inequalities for
. As a byproduct, Sobolev affine trace-type inequalities for  and local Sobolev-type trace inequalities for
and local Sobolev-type trace inequalities for  are established.
are established.