This study examined the operation of resources as a mechanism underlying the relationship between career adaptability and career satisfaction. Based on career construction theory and conservation of resources theory, we examined the interactive effects of career adaptability, career satisfaction, person–job fit, and job uncertainty. The results of two-wave data collection from 234 full-time workers revealed that employees with stronger career adaptability were more likely to report career satisfaction. The full mediating effect was found of person–job fit. Specifically, we found that career adaptability enhances person–job fit, which results in greater career satisfaction. Additional analysis revealed that job uncertainty interferes with the mediation model. We identified a new antecedent of career satisfaction (i.e., person–job fit) and revealed the functional mechanism underlying the effect of this antecedent. This study provides novel insights valuable to the field of career management.

Against the common wisdom that wall slip plays only a minor role in global flow characteristics, here we demonstrate theoretically for the displacement of a long bubble in a slippery channel that the well-known Bretherton $2/3$ law can break down due to a fraction of wall slip with the slip length $\lambda $ much smaller than the channel depth $R$. This breakdown occurs when the film thickness $h_{\infty } $ is smaller than $\lambda $, corresponding to the capillary number $Ca$ below the critical value $Ca^{\ast } \sim (\lambda /R)^{3 / 2}$. In this strong slip regime, a new quadratic law $h_{\infty } /R \sim Ca^{2} (R/\lambda )^{2}$ is derived for a film much thinner than that predicted by the Bretherton law. Moreover, both the $2/3$ and the quadratic laws can be unified into the effective $2/3$ law, with the viscosity $\mu $ replaced by an apparent viscosity $\mu _{app}= \mu h_{\infty } /({\lambda } + h_{\infty })$. A similar extension can also be made for coating over textured surfaces where apparent slip lengths are large. Further insights can be gained by making a connection with drop spreading. We find that the new quadratic law can lead to $\theta _{d} \propto Ca^{1 / 2} $ for the apparent dynamic contact angle of a spreading droplet, subsequently making the spreading radius grow with time as $r \propto t^{1 / 8}$. In addition, the precursor film is found to possess $\ell _{f} \propto Ca^{ - 1 / 2}$ in length and therefore spreads as $\ell _{f} \propto t^{1 / 3}$ in an anomalous diffusion manner. All these features are accompanied by no-slip-to-slip transitions sensitive to the amount of slip, markedly different from those on no-slip surfaces. Our findings not only provide plausible accounts for some apparent departures from no-slip predictions seen in experiments, but also offer feasible alternatives for assessing wall slip effects experimentally.

High saturation magnetization soft magnetic materials are required for future high-density recording heads as well as high frequency inductors. In this work, (Fe0.7Co0.3)1−xNx (or in short FeCoN) alloy films were synthesized with a high saturation magnetization of 24.5 kG, a hard axis coercivity of 5 Oe, an easy axis coercivity of 18 Oe, and a resistivity of 55 μΩcm. The FeCoN film sandwiched between two permalloy layers (5 nm) shows very good magnetic softness, a low hard axis coercivity of 0.6 Oe, an easy axis coercivity of 7.8 Oe, an excellent in-plane uniaxial anisotropy with an anisotropy of about 20 Oe, an initial permeability of 1000, and a roll-off frequency of 1.5 GHz. In order to understand the effect of the permalloy layers on the FeCoN layer, we fabricated four film structures: single layer FeCoN film; FeCoN film sandwiched between two permalloy layers on both sides; FeCoN film with one permalloy layer as the underlayer; and FeCoN film with one permalloy layer as caplayer. All these film structures were both magnetically and structurally characterized and compared. Structural characterization shows that there is no significant difference in the grain size of the FeCoN single layer and the FeCoN layer sandwiched between two permalloy layers. The four film structures have almost the same amount of compressive stress, about −300 MPa; and their saturation magnetostriction constants are also very close, in the range of 39.6×10−6 to 44.3×10−6. Difference in the crystallographic textures was observed in the pole figures for the FeCoN single layer and FeCoN film with permalloy underlayer.

In [2], H. Delange gives the following characterization of the sine function.

Theorem A. f(x)=sin x is the only infinitely differentiable real-valued function on the real line such that f'(O)= 1 and

for all real x and n = 0,1,2,….

It is clear that, if f satisfies (1), then the analytic continuation of f is an entire function satisfying

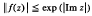
for all z in the complex plane. Hence f is of at most order one and type one. In this note, we prove the following theorem.

We give the representation formula of a periodic function with period one in terms of its translated means on the unit interval. We also give an application of this formula to a boundary value problem.

For a nonconstant L2 (−π, π) function f, we prove that and that the inequalities are sharp.

We give some sufficient conditions to guarantee the uniqueness of certain mean boundary value problems for a circle. Also we show that, in general, we cannot expect uniqueness of the problem for an arc unless the function is analytic in a neighborhood of the unit circle or some shifted means of the function are also known.

We give the representation formula of a function in a disc in terms of its arithmetic means on the boundary. We also give applications of this formula to the solutions of some elementary differential equations with prescribed means of boundary or initial data.