In this paper, we use the Riemann zeta function ζ(x) and the Bessel zeta function ζμ(x) to study the log behaviour of combinatorial sequences. We prove that ζ(x) is log-convex for x > 1. As a consequence, we deduce that the sequence {|B2n|/(2n)!}n ≥ 1 is log-convex, where Bn is the nth Bernoulli number. We introduce the function θ(x) = (2ζ(x)Γ(x + 1)) 1/x, where Γ(x) is the gamma function, and we show that logθ(x) is strictly increasing for x ≥ 6. This confirms a conjecture of Sun stating that the sequence 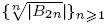is strictly increasing. Amdeberhan et al. defined the numbers an(μ) = 2 2n+1 (n + 1)!(μ+ 1)nζμ(2n) and conjectured that the sequence {an(μ)}n≥1 is log-convex for μ = 0 and μ = 1. By proving that ζμ(x) is log-convex for x > 1 and μ > -1, we show that the sequence {an(≥)}n>1 is log-convex for any μ > - 1. We introduce another function θμ,(x) involving ζμ(x) and the gamma function Γ(x) and we show that logθμ(x) is strictly increasing for x > 8e(μ + 2)2. This implies that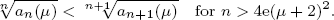

Based on Dobinski’s formula, we prove that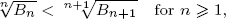

where Bn is the nth Bell number. This confirms another conjecture of Sun. We also establish a connection between the increasing property of 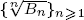and Holder’s inequality in probability theory.

We consider a class of strongly $q$ -log-convex polynomials based on a triangular recurrence relation with linear coefficients, and we show that the Bell polynomials, the Bessel polynomials, the Ramanujan polynomials and the Dowling polynomials are strongly $q$ -log-convex. We also prove that the Bessel transformation preserves log-convexity.