12 results
The Probability of Non-Existence of a Subgraph in a Moderately Sparse Random Graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 4 / July 2018
- Published online by Cambridge University Press:
- 09 May 2018, pp. 672-715
-
- Article
- Export citation
OIL PRODUCTION MODELS WITH NORMAL RATE CURVES
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 25 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 31 March 2011, pp. 205-217
-
- Article
- Export citation
Poisson Approximation of the Number of Cliques in Random Intersection Graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 826-840
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
First Occurrence in Pairs of Long Words: A Penney-ante Conjecture of Pevzner
-
- Journal:
- Combinatorics, Probability and Computing / Volume 4 / Issue 3 / September 1995
- Published online by Cambridge University Press:
- 12 September 2008, pp. 279-285
-
- Article
- Export citation
The Vertex Degree Distribution of Passive Random Intersection Graph Models
-
- Journal:
- Combinatorics, Probability and Computing / Volume 17 / Issue 4 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 549-558
-
- Article
- Export citation
Logical limit laws for logarithmic structures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 140 / Issue 3 / May 2006
- Published online by Cambridge University Press:
- 26 April 2006, pp. 537-544
- Print publication:
- May 2006
-
- Article
- Export citation
ASYMPTOTIC ENUMERATION AND LOGICAL LIMIT LAWS FOR EXPANSIVE MULTISETS AND SELECTIONS
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 22 February 2006, pp. 252-272
- Print publication:
- February 2006
-
- Article
- Export citation
LOGARITHMIC COMBINATORIAL STRUCTURES: A PROBABILISTIC APPROACH (EMS Monographs in Mathematics) By RICHARD ARRATIA, A. D. BARBOUR and SIMON TAVARÉ: 363 pp., €69.00, ISBN 3-03719-000-0 (European Mathematical Society, 2003)
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 08 February 2005, pp. 157-159
- Print publication:
- January 2005
-
- Article
- Export citation
Information Loss in Top to Random Shuffling
-
- Journal:
- Combinatorics, Probability and Computing / Volume 11 / Issue 6 / November 2002
- Published online by Cambridge University Press:
- 21 November 2002, pp. 607-627
-
- Article
- Export citation
Information Loss in Riffle Shuffling
-
- Journal:
- Combinatorics, Probability and Computing / Volume 11 / Issue 1 / January 2002
- Published online by Cambridge University Press:
- 14 February 2002, pp. 79-95
-
- Article
- Export citation
Total Variation Asymptotics for Refined Poisson Process Approximations of Random Logarithmic Assemblies
-
- Journal:
- Combinatorics, Probability and Computing / Volume 8 / Issue 6 / November 1999
- Published online by Cambridge University Press:
- 01 November 1999, pp. 567-598
-
- Article
- Export citation
Explicit Limits of Total Variation Distance in Approximations of Random Logarithmic Assemblies by Related Poisson Processes
-
- Journal:
- Combinatorics, Probability and Computing / Volume 6 / Issue 1 / March 1997
- Published online by Cambridge University Press:
- 01 March 1997, pp. 87-105
-
- Article
- Export citation



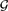
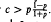 . For |
. For |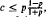 , then the conjecture is true when
, then the conjecture is true when 