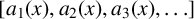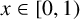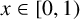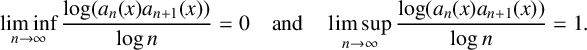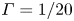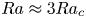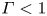1593 results
ASYMPTOTIC BEHAVIOUR FOR PRODUCTS OF CONSECUTIVE PARTIAL QUOTIENTS IN CONTINUED FRACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-12
-
- Article
- Export citation
Mood disorders influencing endometriosis and adenomyosis: Mendelian randomisation study
-
- Journal:
- BJPsych Open / Volume 10 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 16 April 2024, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Biochemical and immunological characterization of excretory–secretory products of Vesicocoelium solenophagum and plasma proteins of its bivalve host, Sinonovacula constricta
-
- Journal:
- Journal of Helminthology / Volume 75 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 12 April 2024, pp. 279-284
-
- Article
- Export citation
The making of a goddess: rethinking the history of the cult of Zhunti (Cundī) in China
-
- Journal:
- Journal of the Royal Asiatic Society , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-23
-
- Article
-
- You have access
- HTML
- Export citation
Predictors of SARS-CoV-2 transmission in congregate living settings: a multicenter prospective study
-
- Journal:
- Infection Control & Hospital Epidemiology , First View
- Published online by Cambridge University Press:
- 02 April 2024, pp. 1-6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical study on the mechanism of drag modulation by dispersed drops in two-phase Taylor–Couette turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 984 / 10 April 2024
- Published online by Cambridge University Press:
- 01 April 2024, R3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of dietary selenium intake on cardiovascular disease: A retrospective cohort study based on China Health and Nutrition Survey (CHNS) data
-
- Journal:
- Public Health Nutrition / Accepted manuscript
- Published online by Cambridge University Press:
- 27 March 2024, pp. 1-23
-
- Article
-
- You have access
- Open access
- Export citation
Necessary and sufficient conditions for ground state solutions to planar Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 March 2024, pp. 1-22
-
- Article
- Export citation
Brightness enhancement on random-distributed-feedback Raman fiber lasers pumped by multimode diodes
-
- Journal:
- High Power Laser Science and Engineering / Accepted manuscript
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1-21
-
- Article
-
- You have access
- Open access
- Export citation
Exploring adolescents’ experiences of talking about race, ethnicity and culture during dialectical behaviour therapy (DBT): a qualitative study using thematic analysis
-
- Journal:
- The Cognitive Behaviour Therapist / Volume 17 / 2024
- Published online by Cambridge University Press:
- 05 March 2024, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Manglietia ventii blooms for the first time in Kunming Botanical Garden
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition to fully developed turbulence in liquid-metal convection facilitated by spatial confinement
-
- Journal:
- Journal of Fluid Mechanics / Volume 981 / 25 February 2024
- Published online by Cambridge University Press:
- 23 February 2024, R2
-
- Article
- Export citation
Adsorption of atrazine and paraquat on montmorillonite loaded with layered double hydroxide and active site energy distribution analysis
-
- Journal:
- Clay Minerals , FirstView
- Published online by Cambridge University Press:
- 19 February 2024, pp. 1-13
-
- Article
- Export citation
Does CFO Board Membership Benefit Shareholders? The Case of Corporate Acquisitions
-
- Journal:
- Journal of Financial and Quantitative Analysis / Accepted manuscript
- Published online by Cambridge University Press:
- 13 February 2024, pp. 1-61
-
- Article
- Export citation
Utility of routine post-admission testing for SARS-CoV-2 in a rehabilitation facility
-
- Journal:
- Antimicrobial Stewardship & Healthcare Epidemiology / Volume 4 / Issue 1 / 2024
- Published online by Cambridge University Press:
- 12 February 2024, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
2 - The Secret Garden of Candidate Selection and Women’s Political Participation
-
-
- Book:
- Putting Women Up
- Published by:
- ISEAS–Yusof Ishak Institute
- Published online:
- 18 April 2024
- Print publication:
- 06 February 2024, pp 32-56
-
- Chapter
- Export citation
The relationship between social media use and psychosocial outcomes in older adults: A systematic review
-
- Journal:
- International Psychogeriatrics , First View
- Published online by Cambridge University Press:
- 30 January 2024, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How adolescents’ lives were disrupted over the course of the COVID-19 pandemic: A longitudinal investigation in 12 cultural groups in 9 nations from March 2020 to July 2022
-
- Journal:
- Development and Psychopathology , First View
- Published online by Cambridge University Press:
- 26 January 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
9 - The ‘Effect Doctrine’ and the Extraterritorial Application of Chinese National Laws
- from Part III - Selected Areas of Chinese State Practice
-
-
- Book:
- The Cambridge Handbook of China and International Law
- Published online:
- 04 January 2024
- Print publication:
- 18 January 2024, pp 181-200
-
- Chapter
- Export citation