Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-16T22:03:09.969Z Has data issue: false hasContentIssue false
  • English
  • Français

Manipulative Waiters with Probabilistic Intuition

Part of: Graph theory Game theory

Published online by Cambridge University Press:  21 December 2015

MAŁGORZATA BEDNARSKA-BZDȨGA ,
DAN HEFETZ ,
MICHAEL KRIVELEVICH  and
TOMASZ ŁUCZAK
MAŁGORZATA BEDNARSKA-BZDȨGA
Affiliation:
Faculty of Mathematics and CS, Adam Mickiewicz University, Poznań, Poland (e-mail: mbed@amu.edu.pl, tomasz@amu.edu.pl)
DAN HEFETZ
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK (e-mail: danny.hefetz@gmail.com)
MICHAEL KRIVELEVICH
Affiliation:
School of Mathematical Sciences, Sackler Faculty of Exact Sciences, Tel Aviv University, 6997801, Israel (e-mail: krivelev@post.tau.ac.il)
TOMASZ ŁUCZAK
Affiliation:
Faculty of Mathematics and CS, Adam Mickiewicz University, Poznań, Poland (e-mail: mbed@amu.edu.pl, tomasz@amu.edu.pl)
Get access Rights & Permissions [Opens in a new window]

Abstract

For positive integers n and q and a monotone graph property 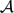$\mathcal{A}$, we consider the two-player, perfect information game WC(n, q, 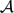$\mathcal{A}$), which is defined as follows. The game proceeds in rounds. In each round, the first player, called Waiter, offers the second player, called Client, q + 1 edges of the complete graph Kn which have not been offered previously. Client then chooses one of these edges which he keeps and the remaining q edges go back to Waiter. If, at the end of the game, the graph which consists of the edges chosen by Client satisfies the property 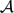$\mathcal{A}$, then Waiter is declared the winner; otherwise Client wins the game. In this paper we study such games (also known as Picker–Chooser games) for a variety of natural graph-theoretic parameters, such as the size of a largest component or the length of a longest cycle. In particular, we describe a phase transition type phenomenon which occurs when the parameter q is close to n and is reminiscent of phase transition phenomena in random graphs. Namely, we prove that if q ⩾ (1 + ϵ)n, then Client can avoid components of order cϵ−2 ln n for some absolute constant c > 0, whereas for q ⩽ (1 − ϵ)n, Waiter can force a giant, linearly sized component in Client's graph. In the second part of the paper, we prove that Waiter can force Client's graph to be pancyclic for every q ⩽ cn, where c > 0 is an appropriate constant. Note that this behaviour is in stark contrast to the threshold for pancyclicity and Hamiltonicity of random graphs.

MSC classification

Primary: 91A43: Games involving graphs
Secondary: 91A46: Combinatorial games 05C38: Paths and cycles 05C80: Random graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 6 , November 2016 , pp. 823 - 849
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ajtai, M., Komlós, J. and Szemerédi, E. (1985) First occurrence of Hamilton cycles in random graphs. In Cycles in Graphs, Vol. 115 of North-Holland Mathematics Studies, North-Holland, pp. 173–178.Google Scholar
[2] Antoniuk, S., Grosu, C. and Narins, L. On the connectivity Waiter–Client game. arXiv:1510.05852 Google Scholar
[3] Beck, J. (1982) Remarks on positional games. Acta Math. Acad. Sci. Hungar. 40 65–71.Google Scholar
[4] Beck, J. (1985) Random graphs and positional games on the complete graph. Ann. Discrete Math. 28 7–13.Google Scholar
[5] Beck, J. (2002) Positional games and the second moment method. Combinatorica 22 169–216.Google Scholar
[6] Beck, J. (2008) Combinatorial Games: Tic-Tac-Toe Theory , Vol. 14 of Encyclopedia of Mathematics and its Applications, Cambridge University Press.Google Scholar
[7] Bednarska-Bzdega, M. (2013) On weight function methods in Chooser–Picker games. Theoret. Comput. Sci. 475 21–33.CrossRefGoogle Scholar
[8] Bednarska-Bzdega, M., Hefetz, D. and Łuczak, T. Picker–Chooser fixed graph games. J. Combin. Theory Ser. B, to appear. arXiv:1402.7308 Google Scholar
[9] Bednarska, M. and Łuczak, T. (2001) Biased positional games and the phase transition. Random Struct. Alg. 18 141–152.Google Scholar
[10] Bollobás, B. (1984) The evolution of sparse graphs. In Graph Theory and Combinatorics, Academic Press, pp. 35–57.Google Scholar
[11] Bollobás, B. (2001) Random Graphs, second edition, Cambridge University Press.Google Scholar
[12] Chvátal, V. and Erdős, P. (1978) Biased positional games. Ann. Discrete Math. 2 221–228.Google Scholar
[13] Cooper, C. and Frieze, A. M. (1990) Pancyclic random graphs. In Random Graphs '87, Wiley, pp. 29–39.Google Scholar
[14] Csernenszky, A. (2010) The Picker–Chooser diameter game. Theoret. Comput. Sci. 411 3757–3762.Google Scholar
[15] Csernenszky, A., Mándity, C. I. and Pluhár, A. (2009) On Chooser–Picker positional games. Discrete Math. 309 5141–5146.Google Scholar
[16] Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5 17–61.Google Scholar
[17] Erdős, P. and Selfridge, J. L. (1973) On a combinatorial game. J. Combin. Theory Ser. A 14 298–301.Google Scholar
[18] Ferber, A., Krivelevich, M. and Naves, H. (2015) Generating random graphs in biased Maker-Breaker games, Random Struct. Alg., 47, 615–634.Google Scholar
[19] Friedman, J. and Pippenger, N. (1987) Expanding graphs contain all small trees. Combinatorica 7 71–76.Google Scholar
[20] Gebauer, H. and Szabó, T. (2009) Asymptotic random graph intuition for the biased connectivity game. Random Struct. Alg. 35 431–443.CrossRefGoogle Scholar
[21] Hales, A. W. and Jewett, R. I. (1963) Regularity and positional games. Trans. Amer. Math. Soc. 106 222–229.CrossRefGoogle Scholar
[22] Hefetz, D., Krivelevich, M., Stojaković, M. and Szabó, T. (2010) Avoider–Enforcer: The rules of the game. J. Combin. Theory Ser. A 117 152–163.CrossRefGoogle Scholar
[23] Hefetz, D., Krivelevich, M., Stojaković, M. and Szabó, T. (2014) Positional Games, Birkhäuser.Google Scholar
[24] Hefetz, D., Krivelevich, M. and Szabó, T. (2007) Avoider–Enforcer games. J. Combin. Theory Ser. A 114 840–853.CrossRefGoogle Scholar
[25] Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.Google Scholar
[26] Komlós, J. and Szemerédi, E. (1983) Limit distribution for the existence of Hamiltonian cycles in a random graph. Discrete Math. 43 55–63.Google Scholar
[27] Krivelevich, M. (2011) The critical bias for the Hamiltonicity game is (1 + o(1))n/ lnn. J. Amer. Math. Soc. 24 125–131.Google Scholar
[28] Krivelevich, M. and Sudakov, B. (2013) The phase transition in random graphs: A simple proof. Random Struct. Alg. 43 131–138.Google Scholar
[29] Krivelevich, M. and Szabó, T. (2008) Biased positional games and small hypergraphs with large covers. Electron. J. Combin. 15 R70.Google Scholar
[30] Lehman, A. (1964) A solution of the Shannon switching game. J. Soc. Indust. Appl. Math. 12 687–725.Google Scholar
[31] Łuczak, T. (1991) Cycles in random graphs. Discrete Math. 98 231–236.Google Scholar
[32] Pósa, L. (1976) Hamiltonian circuits in random graphs. Discrete Math. 14 359–364.Google Scholar
[33] West, D. B. (2001) Introduction to Graph Theory, second edition, Prentice Hall.Google Scholar