Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Del Moral, Pierre
and
Hadjiconstantinou, Nicolas G.
2010.
An introduction to probabilistic methods with applications.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 44,
Issue. 5,
p.
805.
Lejay, Antoine
2011.
Simulation of a stochastic process in a discontinuous layered medium.
Electronic Communications in Probability,
Vol. 16,
Issue. none,
Lejay, Antoine
and
Pichot, Géraldine
2012.
Simulating diffusion processes in discontinuous media: A numerical scheme with constant time steps.
Journal of Computational Physics,
Vol. 231,
Issue. 21,
p.
7299.
Martinez, Miguel
and
Talay, Denis
2012.
One-dimensional parabolic diffraction equations: pointwise estimates and discretization of related stochastic differential equations with weighted local times.
Electronic Journal of Probability,
Vol. 17,
Issue. none,
Étoré, Pierre
and
Martinez, Miguel
2012.
On the existence of a time inhomogeneous skew Brownian motion and some related laws.
Electronic Journal of Probability,
Vol. 17,
Issue. none,
Lejay, Antoine
and
Maire, Sylvain
2013.
New Monte Carlo schemes for simulating diffusions in discontinuous media.
Journal of Computational and Applied Mathematics,
Vol. 245,
Issue. ,
p.
97.
Mackoy, Travis
Harris, Robert C.
Johnson, Jesse
Mascagni, Michael
and
Fenley, Marcia O.
2013.
Numerical Optimization of a Walk-on-Spheres Solver for the Linear Poisson-Boltzmann Equation.
Communications in Computational Physics,
Vol. 13,
Issue. 1,
p.
195.
Talay, Denis
2014.
Advances in Numerical Simulation in Physics and Engineering.
Vol. 3,
Issue. ,
p.
267.
Bossy, Mireille
and
Jabir, Jean-François
2015.
Lagrangian stochastic models with specular boundary condition.
Journal of Functional Analysis,
Vol. 268,
Issue. 6,
p.
1309.
Maire, Sylvain
and
Simon, Martin
2015.
A partially reflecting random walk on spheres algorithm for electrical impedance tomography.
Journal of Computational Physics,
Vol. 303,
Issue. ,
p.
413.
Talay, Denis
2015.
Encyclopedia of Applied and Computational Mathematics.
p.
1327.
Lejay, Antoine
and
Pichot, Géraldine
2016.
Simulating diffusion processes in discontinuous media: Benchmark tests.
Journal of Computational Physics,
Vol. 314,
Issue. ,
p.
384.
Maire, Sylvain
and
Nguyen, Giang
2016.
Stochastic finite differences for elliptic diffusion equations in stratified domains.
Mathematics and Computers in Simulation,
Vol. 121,
Issue. ,
p.
146.
Zhang, P.
2017.
Research on Electron Emission from Dielectric Materials by a Monte Carlo Method.
Moscow University Physics Bulletin,
Vol. 72,
Issue. 6,
p.
574.
Pajor-Gyulai, Zs.
and
Salins, M.
2017.
On dynamical systems perturbed by a null-recurrent motion: The general case.
Stochastic Processes and their Applications,
Vol. 127,
Issue. 6,
p.
1960.
Lejay, Antoine
2018.
Estimation of the bias parameter of the skew random walk and application to the skew Brownian motion.
Statistical Inference for Stochastic Processes,
Vol. 21,
Issue. 3,
p.
539.
Lejay, Antoine
2018.
A Monte Carlo estimation of the mean residence time in cells surrounded by thin layers.
Mathematics and Computers in Simulation,
Vol. 143,
Issue. ,
p.
65.
Lejay, Antoine
Lenôtre, Lionel
and
Pichot, Géraldine
2019.
An exponential timestepping algorithm for diffusion with discontinuous coefficients.
Journal of Computational Physics,
Vol. 396,
Issue. ,
p.
888.
Bai, Yizhou
and
Guo, Zhiyu
2019.
An Empirical Investigation to the “Skew” Phenomenon in Stock Index Markets: Evidence from the Nikkei 225 and Others.
Sustainability,
Vol. 11,
Issue. 24,
p.
7219.
Lejay, Antoine
Mordecki, Ernesto
and
Torres, Soledad
2019.
Two consistent estimators for the skew Brownian motion.
ESAIM: Probability and Statistics,
Vol. 23,
Issue. ,
p.
567.
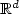 . This family of operators includes the case of the
linearized Poisson-Boltzmann equation used to
compute the electrostatic free energy of a molecule.
More precisely, we explicitly construct a Markov process whose
infinitesimal generator belongs to this family, as the solution of a SDE
including a non standard local time term related to the interface
of discontinuity. We then prove an extended
Feynman-Kac formula for the Poisson-Boltzmann equation.
This formula allows us to justify
various probabilistic numerical methods to
approximate the free energy of a molecule.
We analyse the convergence rate of these simulation procedures and
numerically compare them on idealized molecules models.
. This family of operators includes the case of the
linearized Poisson-Boltzmann equation used to
compute the electrostatic free energy of a molecule.
More precisely, we explicitly construct a Markov process whose
infinitesimal generator belongs to this family, as the solution of a SDE
including a non standard local time term related to the interface
of discontinuity. We then prove an extended
Feynman-Kac formula for the Poisson-Boltzmann equation.
This formula allows us to justify
various probabilistic numerical methods to
approximate the free energy of a molecule.
We analyse the convergence rate of these simulation procedures and
numerically compare them on idealized molecules models.




