Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-18T16:17:33.712Z Has data issue: false hasContentIssue false
  • English
  • Français

NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES 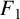$F_1$

Part of: Sequences and sets Basic hypergeometric functions Elementary number theory

Published online by Cambridge University Press:  18 April 2024

XIAOXIA WANG Open the ORCID record for XIAOXIA WANG [Opens in a new window]  and
WENJIE YU
XIAOXIA WANG*
Affiliation:
Department of Mathematics, Shanghai University, Newtouch Center for Mathematics of Shanghai University, Shanghai 200444, PR China
WENJIE YU
Affiliation:
Department of Mathematics, Shanghai University, Newtouch Center for Mathematics of Shanghai University, Shanghai 200444, PR China e-mail: wenjieyu@shu.edu.cn
*
e-mail: xiaoxiawang@shu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Liu [‘Supercongruences for truncated Appell series’, Colloq. Math. 158(2) (2019), 255–263] and Lin and Liu [‘Congruences for the truncated Appell series 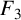$F_3$ and 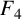$F_4$’, Integral Transforms Spec. Funct. 31(1) (2020), 10–17] confirmed four supercongruences for truncated Appell series. Motivated by their work, we give a new supercongruence for the truncated Appell series 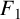$F_{1}$, together with two generalisations of this supercongruence, by establishing its q-analogues.

Keywords

truncated Appell seriessupercongruencesq-congruencescyclotomic polynomial

MSC classification

Primary: 33D15: Basic hypergeometric functions in one variable, $_rphi_s$
Secondary: 11A07: Congruences; primitive roots; residue systems 11B65: Binomial coefficients; factorials; $q$-identities
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 8
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by National Natural Science Foundation of China (No. 12371331) and Natural Science Foundation of Shanghai (No. 22ZR1424100).

References

Gasper, G. and Rahman, M., Basic Hypergeometric Series, 2nd edn, Encyclopedia of Mathematics and Its Applications, 96 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Guo, V. J. W., ‘A new $q$ -analogue of Van Hamme’s (A.2) supercongruence’, Bull. Aust. Math. Soc. 107(1) (2023), 22–30.CrossRefGoogle Scholar
Guo, V. J. W. and Schlosser, M. J., ‘Some $q$ -supercongruences from transformation formulas for basic hypergeometric series’, Constr. Approx. 53(1) (2021), 155–200.CrossRefGoogle Scholar
Guo, V. J. W. and Schlosser, M. J., ‘A family of $q$ -supercongruences modulo the cube of a cyclotomic polynomial’, Bull. Aust. Math. Soc. 105(2) (2022), 296–302.CrossRefGoogle Scholar
Guo, V. J. W. and Zudilin, W., ‘A $q$ -microscope for supercongruences’, Adv. Math. 346 (2019), 329–358.CrossRefGoogle Scholar
He, H. and Wang, X., ‘Some congruences that extend Van Hamme’s (D.2) supercongruence’, J. Math. Anal. Appl. 527(1) (2023), Article no. 127344.CrossRefGoogle Scholar
He, H. and Wang, X., ‘Two curious $q$ -supercongruences and their extensions’, Forum Math., to appear; doi:10.1515/forum-2023-0164.CrossRefGoogle Scholar
Lin, K.-Y. and Liu, J.-C., ‘Congruences for the truncated Appell series ${F}_3$ and ${F}_4$ ’, Integral Transforms Spec. Funct. 31(1) (2020), 10–17.CrossRefGoogle Scholar
Liu, J.-C., ‘Supercongruences for truncated Appell series’, Colloq. Math. 158(2) (2019), 255–263.CrossRefGoogle Scholar
Liu, J.-C. and Petrov, F., ‘Congruences on sums of $q$ -binomial coefficents’, Adv. Appl. Math. 116(2020), Article no. 102003.CrossRefGoogle Scholar
Liu, Y. and Wang, X., ‘Further $q$ -analogues of the (G.2) supercongruence of Van Hamme’, Ramanujan J. 59(3) (2020), 791–802.CrossRefGoogle Scholar
Slater, L. J., Generalized Hypergeometric Functions (Cambridge University Press, Cambridge, 1996).Google Scholar
Wang, X. and Xu, C., ‘ $q$ -Supercongruences on triple and quadruple sums’, Results Math. 78(1) (2023), Article no. 27.CrossRefGoogle Scholar
Wang, X. and Yu, M., ‘A generalisation of a supercongruence on the truncated Appell series ${F}_3$ ’, Bull. Aust. Math. Soc. 107(2) (2023), 296–303.CrossRefGoogle Scholar
Wang, X. and Yu, M., ‘Some new $q$ -supercongruences involving one free parameter’, Rocky Mountain J. Math. 53(4) (2023), 1285–1290.CrossRefGoogle Scholar